GSPO论文阅读

论文：Group Sequence Policy Optimization

摘要

本文提出了一种稳定、高效且性能优异的强化学习算法——Group Sequence Policy Optimization（GSPO），用于训练大语言模型。与以往基于token 级重要性采样的方法不同，GSPO 将重要性采样定义在序列似然层面，并在序列级别进行裁剪、奖励和优化。我们证明了 GSPO 相较于 GRPO 算法在训练效率和性能上具有显著优势，尤其能够稳定Mixture-of-Experts（MoE）的强化学习训练，并有潜力简化 RL 基础设施的设计。这些优势促成了最新 Qwen3 模型的显著提升。

1. 引言

强化学习（Reinforcement Learning, RL）已经成为扩展语言模型规模的关键范式（OpenAI, 2024；DeepSeek-AI, 2025；Qwen, 2025b;a）。通过大规模的 RL 训练，语言模型能够发展出解决复杂问题的能力，例如竞赛级的数学和编程任务，并展现出更深入、更持久的推理过程。

要想在投入更多计算资源的同时成功扩展 RL，首要前提是保持训练过程的稳定性和鲁棒性。然而，当前最先进的 RL 算法，例如 GRPO（Shao 等, 2024），在训练超大规模语言模型时存在严重的稳定性问题，往往导致灾难性、不可逆的模型崩溃（Qwen, 2025a；MiniMax, 2025）。这种不稳定性阻碍了通过持续 RL 训练进一步拓展语言模型能力的努力。

在本文中，我们指出 GRPO 的不稳定性根源在于其算法设计中对重要性采样权重的根本性误用与失效。这一问题引入了高方差的训练噪声，并随着生成响应长度的增加不断累积，同时还被其裁剪机制进一步放大，最终引发模型崩溃。

为解决这些核心局限，我们提出了一种新的 RL 算法——Group Sequence Policy Optimization (GSPO)，用于训练大规模语言模型。GSPO 的关键创新在于其基于序列似然（Zheng 等, 2023）的重要性采样定义，这一设计与重要性采样的基本原理严格对齐。此外，GSPO 将多个响应的归一化奖励作为优势函数进行计算，从而保证了序列级奖励与优化的一致性。

我们的实证评估表明，GSPO 在训练稳定性、效率和性能方面都显著优于 GRPO。尤为关键的是，GSPO 从根本上解决了大规模 Mixture-of-Experts (MoE) 模型 RL 训练中的稳定性难题，无需依赖复杂的稳定化策略，同时展现出简化 RL 基础设施的潜力。这些优势最终促成了最新 Qwen3 模型的卓越性能提升。我们设想，GSPO 将成为一个稳健且可扩展的算法基础，推动大规模语言模型 RL 训练的持续发展。

2. 预备知识

符号说明

本文中，一个由参数 $\theta$ 表示的自回归语言模型被定义为策略 ${\pi }_{\theta }$。我们用 $x$ 表示一个 query，用 $D$ 表示 query 集合。给定query $x$ 的一个响应 $y$，其在策略 ${\pi }_{\theta }$ 下的似然性定义为 ${\pi }_{\theta }(y\mid x)={\prod }_{t=1}^{|y|}{\pi }_{\theta }(y_t\mid x,y_{<t})$，其中 $|y|$ 表示响应 $y$ 的 token 数量。一个查询-响应对 $(x,y)$ 可以通过一个验证器 $r$ 打分，得到一个奖励：$r(x,y)\in [0,1]$

近端策略优化 (Proximal Policy Optimization, PPO)

使用从旧策略 ${\pi }_{{\theta }_{old}}$ 生成的样本，PPO（Schulman 等, 2017）通过裁剪机制将策略更新限制在旧策略的邻近区域内。具体而言，PPO 在策略优化中采用如下目标函数（这里省略了 KL 正则化项以简化说明，因为它并非本文的重点）：

$${\mathcal{J}}_{\text{PPO}}(\theta )={\mathbb{E}}_{x\sim \mathcal{D},y\sim {\pi }_{{\theta }_{\text{old}}}(\cdot \mid x)}\left[\frac{1}{|y|}\sum _{t=1}^{|y|}\min \left(w_t(\theta ){\hat{A}}_t,\mathrm{clip}(w_t(\theta ),1-ϵ,1+ϵ){\hat{A}}_t\right)\right],\text{\hspace{1em}(1)}$$

其中，token $y_t$ 的重要性比率定义为：$w_t(\theta )=\frac{{\pi }_{\theta }(y_t|x,y_{<t})}{{\pi }_{{\theta }_{old}}(y_t|x,y_{<t})}$，而 $y_t$ 的优势函数 ${\hat{A}}_{i,t}$ 由另一个价值模型（value model）进行估计，$ϵ$ 则表示重要性比率的裁剪范围。

PPO 在实际应用中的核心挑战在于它高度依赖价值模型。具体来说，价值模型通常与策略模型规模相当，这会带来相当大的内存和计算负担。此外，该算法的有效性还取决于价值估计的可靠性。而获得一个可靠的价值模型本身就非常困难，进一步要保证它能扩展到更长的响应和更复杂的任务，则是更大的挑战。

群体相对策略优化（Group Relative Policy Optimization, GRPO）GRPO（Shao 等, 2024）通过在同一查询的一组响应中计算每个响应的相对优势，从而绕过了对价值模型的需求。具体而言，GRPO 优化的目标函数如下：

JGRPO(θ)=Ex∼D,{yi}i=1G∼πθold(⋅∣x)[1G∑i=1G1∣yi∣∑t=1∣yi∣min⁡(wi,t(θ)A^i,t,clip⁡(wi,t(θ),1−ϵ,1+ϵ)A^i,t)],(2)\mathcal{J}_{\text{GRPO}}(\theta) = \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot \mid x)} \left[ \frac{1}{G} \sum_{i=1}^{G} \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \min \left( w_{i,t}(\theta) \hat{A}_{i,t}, \ \operatorname{clip}\left(w_{i,t}(\theta), 1 - \epsilon, 1 + \epsilon\right) \hat{A}_{i,t} \right) \right], \tag{2} JGRPO​(θ)=Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​​G1​i=1∑G​∣yi​∣1​t=1∑∣yi​∣​min(wi,t​(θ)A^i,t​, clip(wi,t​(θ),1−ϵ,1+ϵ)A^i,t​)​,(2)

其中 $G$ 是每个查询 $x$ 所生成的响应数量（即group size），token $y_{i,t}$ 的重要性比率和优势 ${\hat{A}}_{i,t}$ 为：

wi,t(θ)=πθ(yi,t∣x,yi,<t)πθold(yi,t∣x,yi,<t),A^i,t=A^i=r(x,yi)−mean({r(x,yi)}i=1G)std({r(x,yi)}i=1G),(3)w_{i,t}(\theta) = \frac{\pi_{\theta}(y_{i,t} \mid x, y_{i,\lt t})}{\pi_{\theta_{\text{old}}}(y_{i,t} \mid x, y_{i,\lt t})}, \quad \hat{A}_{i,t} = \hat{A}_i = \frac{r(x, y_i) - \mathrm{mean}(\{r(x, y_i)\}_{i=1}^G)}{\mathrm{std}(\{r(x, y_i)\}_{i=1}^G)}, \tag{3} wi,t​(θ)=πθold​​(yi,t​∣x,yi,<t​)πθ​(yi,t​∣x,yi,<t​)​,A^i,t​=A^i​=std({r(x,yi​)}i=1G​)r(x,yi​)−mean({r(x,yi​)}i=1G​)​,(3)

其中 $y_i$ 中的所有 token 共享同一个的优势 ${\hat{A}}_i$。

3. 动机

随着模型规模、稀疏性（例如 Mixture-of-Experts 模型）以及响应长度的增长，在强化学习过程中需要更大的 rollout 批量，以最大化硬件利用率。为了提高采样效率，通常的做法是将一个大批量的 rollout 数据划分为多个 mini-batch 来进行梯度更新。

这一过程不可避免地引入了异策略（off-policy）学习情形，即响应 $y$ 是从旧策略 ${\pi }_{{\theta }_{old}}$ 而非当前正在优化的策略 ${\pi }_{\theta }$ 中采样的。这也解释了为什么在 PPO 和 GRPO 中需要引入裁剪机制：它能够防止过度“异策略”的样本参与梯度估计。

尽管裁剪等机制旨在处理这种异策略差异，我们发现 GRPO 中存在一个更为根本的问题：它的目标函数是病态（ill-posed）的。当在大模型上训练长响应任务时，这一问题尤其严重，最终会导致灾难性的模型崩溃。

GRPO 目标函数的病态性源于对重要性采样权重的误用。重要性采样的原理在于：通过对来自行为分布 ${\pi }_{beh}$ 的样本进行重新加权，以此来估计目标分布 ${\pi }_{tar}$ 下某个函数 $f$ 的期望值：

$${\mathbb{E}}_{z\sim {\pi }_{\text{tar}}}\left[f(z)\right]={\mathbb{E}}_{z\sim {\pi }_{\text{beh}}}\left[\frac{{\pi }_{\text{tar}}(z)}{{\pi }_{\text{beh}}(z)}f(z)\right].\text{\hspace{1em}(4)}$$

关键在于，重要性采样依赖于对来自行为分布 ${\pi }_{beh}$ 的多个样本（$N\gg 1$）进行平均，这样重要性权重 $\frac{{\pi }_{tar}(z)}{{\pi }_{beh}(z)}$ 才能有效地纠正分布不匹配的问题。

相比之下，GRPO 在每一个 token 位置 $t$ 上都应用如下的重要性权重：$\frac{{\pi }_{\theta }(y_{i,t}|x,y_{i,<t})}{{\pi }_{{\theta }_{old}}(y_{i,t}|x,y_{i,<t})}$ 然而，由于这个权重仅基于行为策略 ${\pi }_{{\theta }_{old}}(\cdot |x,y_{i,<t})$ 的单一样本 $y_{i,t}$，因此它无法发挥应有的分布修正作用。相反，这种做法会在训练梯度中引入高方差噪声，并在长序列中不断累积，同时被裁剪机制进一步放大。我们在实证中观察到，这可能导致模型出现往往不可逆的崩溃。一旦崩溃发生，即便回退到先前的检查点并精心调整超参数（例如裁剪范围）、延长生成长度或更换 RL 查询，恢复训练也无济于事。

上述现象表明，GRPO 的设计存在根本性问题。token 级的重要性权重的失效指向了一个核心原则：优化目标的单位应当与奖励的单位一致。既然奖励是授予给整个序列的，那么在 token 级别应用异策略（off-policy）校正就显得不合理。由此我们受到启发，放弃 token 级目标，转而探索在序列级别上直接使用重要性权重并进行优化。

4. 算法

4.1 GSPO：群体序列策略优化（Group Sequence Policy Optimization）

在 GRPO 中，token 级的重要性权重 $\frac{{\pi }_{\theta }(y_{i,t}|x,y_{i,<t})}{{\pi }_{{\theta }_{old}}(y_{i,t}|x,y_{i,<t})}$ 存在问题。而我们观察到，在语言生成的语境下，序列级的重要性权重 $\frac{{\pi }_{\theta }(y|x)}{{\pi }_{{\theta }_{old}}(y|x)}$ 具有明确的理论意义：它反映了一个由旧策略 ${\pi }_{{\theta }_{old}}$ 采样得到的响应 $y$ 相对于新策略 ${\pi }_{\theta }(\cdot |x)$ 的偏离程度，这与序列级奖励天然对齐，同时也可以作为裁剪机制的有意义指标。

基于这一直接的观察，我们提出了群体序列策略优化（GSPO） 算法。GSPO 采用如下的序列级优化目标函数：

JGSPO(θ)=Ex∼D,{yi}i=1G∼πθold(⋅∣x)[1G∑i=1Gmin⁡(si(θ)A^i,clip(si(θ),1−ϵ,1+ϵ)A^i)],(5)\mathcal{J}_{\mathrm{GSPO}}(\theta) = \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot|x)} \left[ \frac{1}{G} \sum_{i=1}^G \min \left( s_i(\theta) \hat{A}_i, \ \mathrm{clip}\left(s_i(\theta), 1 - \epsilon, 1 + \epsilon\right) \hat{A}_i \right) \right], \tag{5} JGSPO​(θ)=Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​[G1​i=1∑G​min(si​(θ)A^i​, clip(si​(θ),1−ϵ,1+ϵ)A^i​)],(5)

其中我们采用基于组的优势估计：

A^i=r(x,yi)−mean({r(x,yi)}i=1G)std({r(x,yi)}i=1G),(6)\hat{A}_i = \frac{r(x, y_i) - \mathrm{mean}\left(\{r(x, y_i)\}_{i=1}^G\right)}{\mathrm{std}\left(\{r(x, y_i)\}_{i=1}^G\right)}, \tag{6} A^i​=std({r(x,yi​)}i=1G​)r(x,yi​)−mean({r(x,yi​)}i=1G​)​,(6)

并基于序列似然性（Zheng 等, 2023）定义重要性比率 $s_i(\theta )$ ：

$$s_i(\theta )={\left(\frac{{\pi }_{\theta }(y_i\mid x)}{{\pi }_{{\theta }_{\mathrm{old}}}(y_i\mid x)}\right)}^{\frac{1}{|y_i|}}=\exp \left(\frac{1}{|y_i|}\sum _{t=1}^{|y_i|}\log \frac{{\pi }_{\theta }(y_{i,t}\mid x,y_{i,<t})}{{\pi }_{{\theta }_{\mathrm{old}}}(y_{i,t}\mid x,y_{i,<t})}\right).\text{\hspace{1em}(7)}$$

因此，GSPO 将裁剪操作应用于整个响应序列，而不是单个 token，从而在梯度估计中排除过度“异策略”的样本。这种方式同时契合了序列级奖励与序列级优化。

需要注意的是，我们在 $s_i(\theta )$ 中采用了长度归一化，以降低方差，并将 $s_i(\theta )$ 控制在统一的数值范围内。否则，仅仅少数几个 token 的似然变化就可能导致序列级重要性比率的剧烈波动，而不同长度的响应所对应的重要性比率则需要采用不同的裁剪范围。

我们还注意到，由于重要性比率的定义方式不同，GSPO 与先前的算法（例如 GRPO）在裁剪范围的数量级上通常会存在差异。

4.2 梯度分析

我们可以将 GSPO 目标函数的梯度推导如下（为简洁起见，此处省略裁剪操作）：

∇θJGSPO(θ)=∇θEx∼D,{yi}i=1G∼πθold(⋅∣x)[1G∑i=1Gsi(θ)A^i]=Ex∼D,{yi}i=1G∼πθold(⋅∣x)[1G∑i=1Gsi(θ)A^i⋅∇θlog⁡si(θ)]=Ex∼D,{yi}i=1G∼πθold(⋅∣x)[1G∑i=1G(πθ(yi∣x)πθold(yi∣x))1∣yi∣A^i⋅1∣yi∣∑t=1∣yi∣∇θlog⁡πθ(yi,t∣x,yi,<t)].\begin{align} \nabla_{\theta} \mathcal{J}_{\mathrm{GSPO}}(\theta) &= \nabla_{\theta} \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot|x)} \left[ \frac{1}{G} \sum_{i=1}^G s_i(\theta) \hat{A}_i \right] \tag{8} \\ &= \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot|x)} \left[ \frac{1}{G} \sum_{i=1}^G s_i(\theta) \hat{A}_i \cdot \nabla_{\theta} \log s_i(\theta) \right] \tag{9} \\ &= \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot|x)} \left[ \frac{1}{G} \sum_{i=1}^G \left( \frac{\pi_{\theta}(y_i|x)}{\pi_{\theta_{\mathrm{old}}}(y_i|x)} \right)^{\frac{1}{|y_i|}} \hat{A}_i \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \nabla_{\theta} \log \pi_{\theta}(y_{i,t} | x, y_{i,\lt t}) \right]. \tag{10} \end{align} ∇θ​JGSPO​(θ)​=∇θ​Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​[G1​i=1∑G​si​(θ)A^i​]=Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​[G1​i=1∑G​si​(θ)A^i​⋅∇θ​logsi​(θ)]=Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​​G1​i=1∑G​(πθold​​(yi​∣x)πθ​(yi​∣x)​)∣yi​∣1​A^i​⋅∣yi​∣1​t=1∑∣yi​∣​∇θ​logπθ​(yi,t​∣x,yi,<t​)​.​(8)(9)(10)​

为了进行比较，GRPO目标的梯度如下（注意 ${\hat{A}}_{i,t}={\hat{A}}_i$）：

∇θJGRPO(θ)=∇θEx∼D,{yi}i=1G∼πθold(⋅∣x)[1G∑i=1G1∣yi∣∑t=1∣yi∣wi,t(θ)A^i,t]=Ex∼D,{yi}i=1G∼πθold(⋅∣x)[1G∑i=1GA^i⋅1∣yi∣∑t=1∣yi∣πθ(yi,t∣x,yi,<t)πθold(yi,t∣x,yi,<t)∇θlog⁡πθ(yi,t∣x,yi,<t)].\begin{align} \nabla_{\theta} \mathcal{J}_{\mathrm{GRPO}}(\theta) &= \nabla_{\theta} \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot|x)} \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} w_{i,t}(\theta) \hat{A}_{i,t} \right] \tag{11} \\ &= \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot|x)} \left[ \frac{1}{G} \sum_{i=1}^G \hat{A}_i \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \frac{\pi_{\theta}(y_{i,t} \mid x, y_{i,\lt t})}{\pi_{\theta_{\mathrm{old}}}(y_{i,t} \mid x, y_{i,\lt t})} \nabla_{\theta} \log \pi_{\theta}(y_{i,t} \mid x, y_{i,\lt t}) \right] . \tag{12} \end{align}∇θ​JGRPO​(θ)​=∇θ​Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​​G1​i=1∑G​∣yi​∣1​t=1∑∣yi​∣​wi,t​(θ)A^i,t​​=Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​​G1​i=1∑G​A^i​⋅∣yi​∣1​t=1∑∣yi​∣​πθold​​(yi,t​∣x,yi,<t​)πθ​(yi,t​∣x,yi,<t​)​∇θ​logπθ​(yi,t​∣x,yi,<t​)​.​(11)(12)​

因此，GSPO 与 GRPO 的根本区别在于它们对 token 对数似然梯度的加权方式。在 GRPO 中，token 的权重根据各自的“重要性权重” $\frac{{\pi }_{\theta }(y_{i,t}|x,y_{i,<t})}{{\pi }_{{\theta }_{old}}(y_{i,t}|x,y_{i,<t})}$ 确定。然而，这些不等权重的取值可以在 $(0,1+ϵ]$ （当 $A_i^b>0时$）或 $[1-ϵ,+\infty )$ （当 $A_i^b<0$ 时）间变化，其影响不可忽略，且随着训练的进行可能累积，导致不可预测的后果。

相比之下，GSPO 对一个响应序列中的所有 token 赋予相同的权重，从而消除了 GRPO 中的这一不稳定因素。

4.3 GSPO-token：基于 token 的目标变体

在多轮 RL等场景中，我们可能希望比序列级更细粒度地调整优势函数。为此，我们引入 GSPO 的一个token 级目标变体，称为 GSPO-token，以支持对每个 token 的优势进行定制：

JGSPO-token(θ)=Ex∼D,{yi}i=1G∼πθold(⋅∣x)[1G∑i=1G1∣yi∣∑t=1∣yi∣min⁡(si,t(θ)A^i,t,clip(si,t(θ),1−ϵ,1+ϵ)A^i,t)],\begin{equation} \mathcal{J}_{\mathrm{GSPO\text{-}token}}(\theta) = \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot|x)} \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \min \left( s_{i,t}(\theta) \hat{A}_{i,t}, \, \mathrm{clip}\big(s_{i,t}(\theta), 1-\epsilon, 1+\epsilon\big) \hat{A}_{i,t} \right) \right], \tag{13} \end{equation}JGSPO-token​(θ)=Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​​G1​i=1∑G​∣yi​∣1​t=1∑∣yi​∣​min(si,t​(θ)A^i,t​,clip(si,t​(θ),1−ϵ,1+ϵ)A^i,t​)​,​(13)​

其中

$$\begin{array}{c}{s}_{i,t}(\theta )=\mathrm{sg}\left[s_i(\theta )\right]\cdot \frac{{\pi }_{\theta }(y_{i,t}\mid x,y_{i,<t})}{\mathrm{sg}\left[{\pi }_{\theta }(y_{i,t}\mid x,y_{i,<t})\right]},\end{array}\text{\hspace{1em}(14)}$$

其中 $sg[\cdot ]$ 表示只取数值但停止梯度传播，对应于 PyTorch 中的 detach 操作。GSPO-token 的梯度可以推导如下：

∇θJGSPO-token(θ)=∇θEx∼D,{yi}i=1G∼πθold(⋅∣x)[1G∑i=1G1∣yi∣∑t=1∣yi∣si,t(θ)A^i,t]=Ex∼D,{yi}i=1G∼πθold(⋅∣x)[1G∑i=1Gsi(θ)⋅1∣yi∣∑t=1∣yi∣A^i,t∇θπθ(yi,t∣x,yi,<t)πθ(yi,t∣x,yi,<t)]=Ex∼D,{yi}i=1G∼πθold(⋅∣x)[1G∑i=1G(πθ(yi∣x)πθold(yi∣x))1∣yi∣⋅1∣yi∣∑t=1∣yi∣A^i,t∇θlog⁡πθ(yi,t∣x,yi,<t)].\begin{align} \nabla_{\theta} \mathcal{J}_{\mathrm{GSPO\text{-}token}}(\theta) &= \nabla_{\theta} \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot|x)} \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} s_{i,t}(\theta) \hat{A}_{i,t} \right] \tag{15} \\ &= \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot|x)} \left[ \frac{1}{G} \sum_{i=1}^G s_i(\theta) \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \hat{A}_{i,t} \frac{\nabla_{\theta} \pi_{\theta}(y_{i,t}|x, y_{i,\lt t})}{\pi_{\theta}(y_{i,t}|x, y_{i,\lt t})} \right] \tag{16} \\ &= \mathbb{E}_{x \sim \mathcal{D}, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot|x)} \left[ \frac{1}{G} \sum_{i=1}^G \left( \frac{\pi_{\theta}(y_i|x)}{\pi_{\theta_{\mathrm{old}}}(y_i|x)} \right)^{\frac{1}{|y_i|}} \cdot \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \hat{A}_{i,t} \nabla_{\theta} \log \pi_{\theta}(y_{i,t}|x,y_{i,\lt t}) \right]. \tag{17} \end{align}∇θ​JGSPO-token​(θ)​=∇θ​Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​​G1​i=1∑G​∣yi​∣1​t=1∑∣yi​∣​si,t​(θ)A^i,t​​=Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​​G1​i=1∑G​si​(θ)⋅∣yi​∣1​t=1∑∣yi​∣​A^i,t​πθ​(yi,t​∣x,yi,<t​)∇θ​πθ​(yi,t​∣x,yi,<t​)​​=Ex∼D,{yi​}i=1G​∼πθold​​(⋅∣x)​​G1​i=1∑G​(πθold​​(yi​∣x)πθ​(yi​∣x)​)∣yi​∣1​⋅∣yi​∣1​t=1∑∣yi​∣​A^i,t​∇θ​logπθ​(yi,t​∣x,yi,<t​)​.​(15)(16)(17)​

需要注意的是，项 ${\pi }_{\theta }(y_{i,t}|x,y_{i,<t})sg[{\pi }_{\theta }(y_{i,t|x,y_{i,<t}})]$ 的数值为 1，因此 $s_{i,t}(\theta )$ 在数值上等于 $s_i(\theta )$。比较公式 (5) 与 (13)，以及公式 (10) 与 (17) 可以发现，当我们将响应 $y_i$ 中所有 token 的优势函数设为相同值（即 $A_{i,t}^b=A_i^b$）时，GSPO-token 与 GSPO 在优化目标、裁剪条件以及理论梯度上在数值上是完全一致的。而 GSPO-token 则具备更高的灵活性，能够对每个 token 的优势进行独立调整。

5. 实验与讨论

5.1 实证结果

我们以从 Qwen3-30B-A3B-Base 微调的冷启动模型进行实验，并报告训练奖励曲线以及模型在以下基准上的性能曲线：AIME’24（32 次采样的平均 Pass@1），LiveCodeBench（2024 年 10 月至 2025 年 2 月，8 次采样的平均 Pass@1），CodeForces（Elo 等级）。在 RL 训练过程中，每批 rollout 数据被划分为四个 mini-batch 进行梯度更新。在 GSPO 中，我们将公式 (5) 中的左、右裁剪范围分别设置为 3e-4 和 4e-4。我们以 GRPO 作为基线算法，并将公式 (2) 中的左、右裁剪范围分别设置为 0.2 和 0.27，这些数值经过仔细调优，以确保比较的公平性。

需要注意的是，GRPO 在 MoE RL 的正常收敛中需要依赖 Routing Replay 训练策略（我们将在 §5.3 中进一步讨论），而 GSPO 则无需该策略。

图 1 显示，GSPO 的训练过程始终保持稳定。我们观察到，GSPO 能够通过增加训练计算量、定期更新查询集以及延长生成长度，实现持续的性能提升。此外，GSPO 在训练效率上也优于 GRPO，在相同的训练计算量和消耗的查询数量下，能够获得更高的训练精度和基准性能。最后，我们已成功将 GSPO 应用于最新 Qwen3 模型的 RL 训练，充分证明了 GSPO 在释放大语言模型 RL 扩展能力方面的有效性。

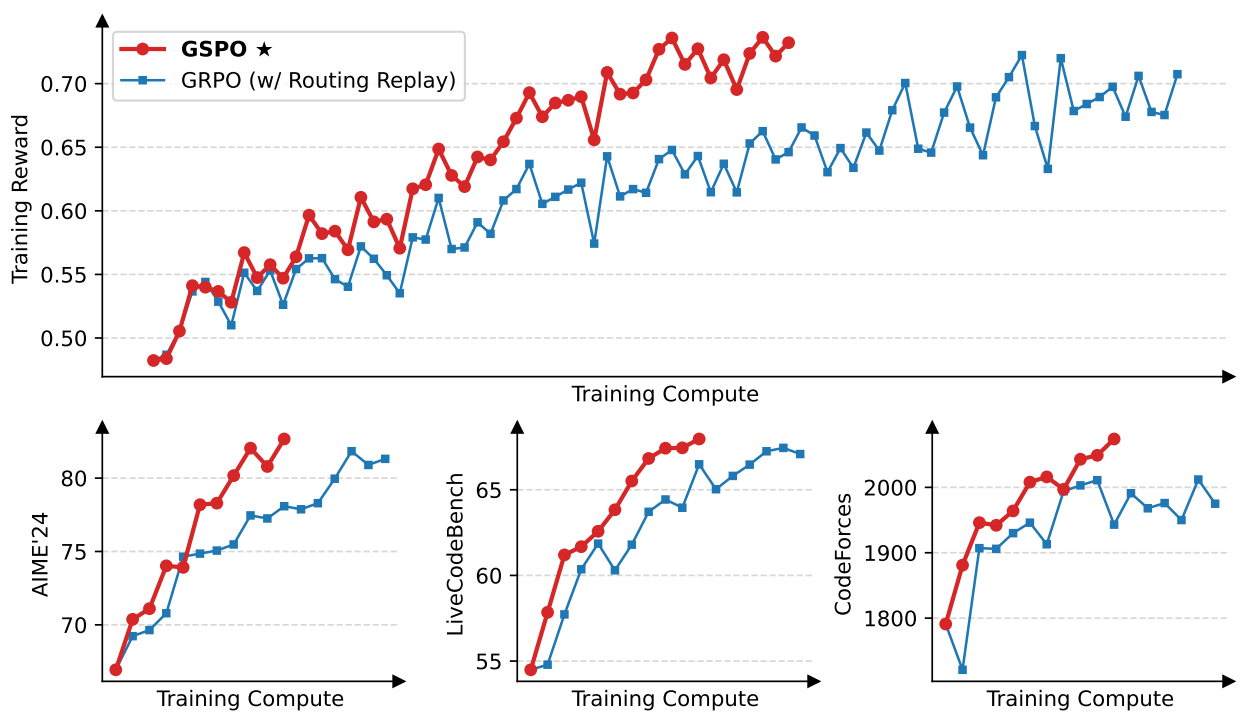
图 1： 从 Qwen3-30B-A3B-Base 微调的冷启动模型的训练曲线。GSPO 的训练效率显著高于 GRPO

5.2 关于裁剪比例的有趣观察

GSPO 与 GRPO 的一个关键区别在于，GSPO 对整个响应序列进行裁剪，而不是对单个 token 进行裁剪。尤其如图 2 所示，我们观察到 GSPO 与 GRPO 在被裁剪 token 的比例上存在两个数量级的差异（即使调整裁剪范围也无法改变这种数量级差异）。然而，尽管 GSPO 裁剪了更多的 token，从而在训练（或梯度估计）中使用了更少的 token，它依然实现了比 GRPO 更高的训练效率。这一反直觉的发现——裁剪大量 token 反而带来更高的训练效率——进一步表明，GRPO 的 token 级梯度估计本质上存在噪声大且样本利用效率低的问题。相比之下，GSPO 的序列级方法提供了更可靠、更有效的学习信号。

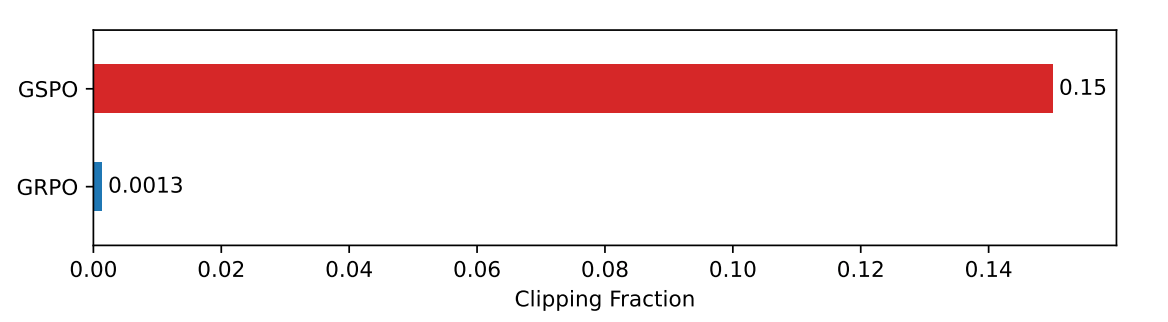
图 2： GSPO 与 GRPO 在 RL 训练过程中被裁剪 token 的平均比例

5.3 GSPO 对 MoE 训练的优势

背景 相比于密集模型的 RL 训练，MoE 模型的稀疏激活特性带来了独特的稳定性挑战。具体来说，我们发现，当采用 GRPO 算法时，MoE 模型的专家激活波动可能导致 RL 训练无法正常收敛。更具体地说，在一次或多次梯度更新后，同一响应所激活的专家可能会发生显著变化。例如，在 48 层的 Qwen3-30B-A3B-Base 模型中，每次 RL 梯度更新后，对于同一个 rollout 样本，新策略 ${\pi }_{\theta }$ 激活的专家中约有 10% 与旧策略 ${\pi }_{{\theta }_{old}}$ 不同。这种现象在更深的 MoE 模型中更加明显，使得 token 级重要性比率 $w_{i,t}(\theta )=\frac{{\pi }_{{\theta }_{old}}(y_{i,t}|x,y_{i,<t})}{{\pi }_{\theta }(y_{i,t}|x,y_{i,<t})}$ 出现剧烈波动并失效（如 §3 和 §4.2 所讨论），从而阻碍 RL 训练的正常收敛。

我们之前的做法 为应对这一挑战，我们此前采用了 Routing Replay 训练策略。具体做法是，将旧策略 ${\pi }_{{\theta }_{old}}$ 中激活的专家进行缓存，并在计算重要性比率 $w_{i,t}(\theta )=\frac{{\pi }_{{\theta }_{old}}(y_{i,t}|x,y_{i,<t})}{{\pi }_{\theta }(y_{i,t}|x,y_{i,<t})}$ 时“重放”这些路由模式。通过这种方式，对于每个 token $y_{i,t},{\pi }_{\theta }(y_{i,t}|x,y_{i,<t})$ 与 ${\pi }_{{\theta }_{old}}(y_{i,t}|x,y_{i,<t})$ 使用相同的激活网络，从而恢复了 token 级重要性比率的稳定性，并确保在梯度更新过程中优化的是一致的激活网络。图 3 表明，Routing Replay 是 GRPO 在 MoE 模型训练中实现正常收敛的关键技术。

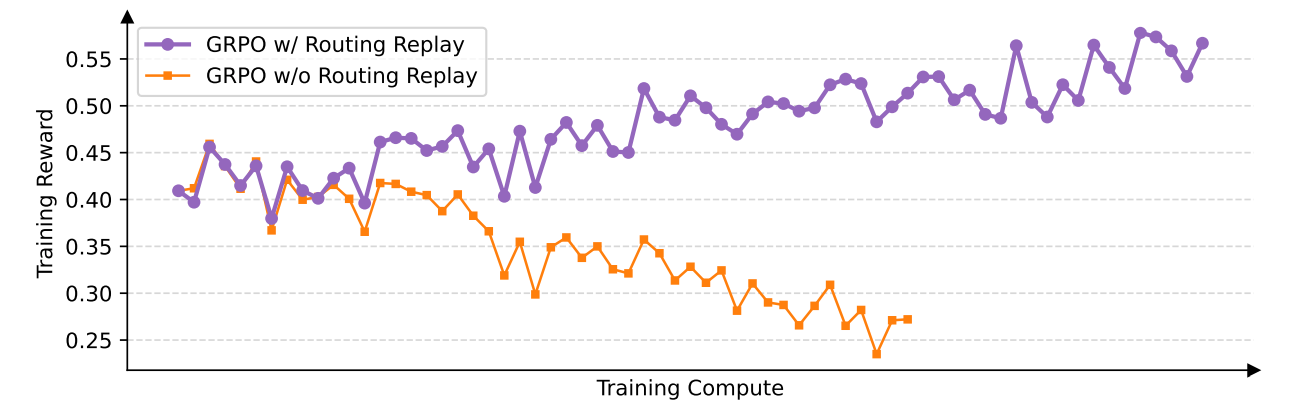
图 3： 在 MoE 模型的 GRPO 训练中，Routing Replay 策略对于实现正常收敛起关键作用

GSPO 的优势 虽然 Routing Replay 能够使 GRPO 在 MoE 模型上的训练正常收敛，但其重复使用路由模式的做法会带来额外的内存和通信开销，并可能限制 MoE 模型的实际容量。相比之下，如图 1 所示，GSPO 消除了对 Routing Replay 的依赖，能够按常规方式计算重要性比率 $s_i(\theta )$、实现正常收敛，并保持稳定优化。其关键洞察在于，GSPO 仅关注序列似然性（即 ${\pi }_{\theta }(y_i|x)$），而对单个 token 的似然性（即 ${\pi }_{\theta }(y_{i,t}|x,y_{i,<t})$)）不敏感。由于 MoE 模型始终保持其语言建模能力，序列似然不会出现剧烈波动。

总之，GSPO 从根本上解决了 MoE 模型中的专家激活波动问题，无需像 Routing Replay 这样的复杂解决方案。这不仅简化并稳定了训练过程，还使模型能够充分发挥其完整容量，而不受人为约束。

5.4 GSPO 对 RL 基础设施的优势

考虑到训练引擎（如 Megatron）与推理引擎（如 SGLang 和 vLLM）之间的精度差异，在实际操作中，我们通常需要使用训练引擎重新计算旧策略 ${\pi }_{{\theta }_{old}}$ 下采样响应的似然值。然而，GSPO 仅使用序列级而非 token 级的似然进行优化，而直观上，序列级似然对精度差异更加容忍。因此，GSPO 使得可以直接使用由推理引擎返回的似然进行优化，从而无需使用训练引擎重新计算。这种特性在部分 rollout、多轮 RL以及训练-推理分离框架等场景中尤为有利。

6. 结论

我们提出了群体序列策略优化（GSPO），一种用于训练大语言模型的新型强化学习算法。遵循重要性采样的基本原理，GSPO 基于序列似然性定义重要性比率，并在序列级别进行裁剪、奖励和优化。与 GRPO 相比，GSPO 在训练稳定性、效率和性能上表现出显著优势，并在大规模 MoE 模型的 RL 训练中展现出特殊的有效性，这为最新 Qwen3 模型的卓越提升奠定了基础。以 GSPO 作为可扩展的算法基石，我们将继续推进 RL 的规模化，并期待由此带来的智能领域的根本性进展。

重要性采样参考