如何制作建筑公司网站手机端网页制作公司

记录一下今天完成的算法题，虽然这个难度是困难，但感觉没有那个560.和为k的子数组和难想，这个题主要就前期遇到个优先队列，因为之前没用过，不太熟悉，剩下的思路感觉都属于正常难度

问题描述

原始思路：优先队列（最大堆）

原始代码使用最大堆（PriorityQueue）存储元素值及其索引，堆顶始终是当前窗口的最大值。但原始代码存在逻辑错误，修正后的代码如下：

import java.util.PriorityQueue;public class Solution {public int[] maxSlidingWindow(int[] nums, int k) {if (nums.length == 0) return new int[0];PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> b[0] - a[0]); // 最大堆// 初始化第一个窗口for (int i = 0; i < k; i++) {pq.offer(new int[]{nums[i], i});}int[] result = new int[nums.length - k + 1];result[0] = pq.peek()[0]; // 第一个窗口的最大值// 滑动窗口for (int i = k; i < nums.length; i++) {pq.offer(new int[]{nums[i], i}); // 1. 加入新元素while (pq.peek()[1] < i - k + 1) {  // 2. 弹出不在窗口内的元素pq.poll();}result[i - k + 1] = pq.peek()[0]; // 3. 记录当前窗口最大值}return result;}
}

核心逻辑

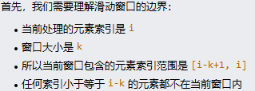
1. 初始化堆：将第一个窗口的元素 [值, 索引] 加入最大堆。
2. 滑动窗口：
   • 加入新元素：将窗口右侧新元素加入堆。
   • 清理无效元素：弹出堆顶所有索引小于 i - k + 1 的元素（这些元素已离开窗口）。
   • 记录最大值：堆顶元素即为当前窗口最大值。

复杂度分析

• 时间复杂度：O(n log n) 每个元素入堆和出堆需 O(log n)，最坏情况下（如单调递增数组）堆中元素累积至 O(n)。
• 空间复杂度：O(n)

缺陷

• 无效元素积累：堆中可能保留大量已离开窗口的元素，导致堆操作效率降低。

在此之上，我们延续优先队列的思路，对代码进行一下优化

优化方案1：单调队列（双端队列）

使用双端队列（Deque）维护一个严格递减的序列，队首始终是当前窗口最大值。时间复杂度优化至 O(n)。

import java.util.Deque;
import java.util.LinkedList;public class Solution {public int[] maxSlidingWindow(int[] nums, int k) {if (nums.length == 0) return new int[0];Deque<Integer> deque = new LinkedList<>(); // 存储索引int[] result = new int[nums.length - k + 1];for (int i = 0; i < nums.length; i++) {// 1. 清理超出窗口的队首元素while (!deque.isEmpty() && deque.peekFirst() < i - k + 1) {deque.pollFirst();}// 2. 从队尾移除小于当前元素的索引while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {deque.pollLast();}deque.offerLast(i); // 3. 当前索引入队// 4. 记录窗口最大值（从第k-1个元素开始）if (i >= k - 1) {result[i - k + 1] = nums[deque.peekFirst()];}}return result;}
}

核心改进

1. 严格递减队列： 每次添加新元素时，从队尾移除所有小于它的元素索引，确保队列严格递减。
2. 队首即最大值： 队首对应元素始终为当前窗口最大值。
3. 即时清理无效元素： 在添加新元素前，先清理离开窗口的队首元素，避免无效积累。

复杂度分析

• 时间复杂度：O(n) 每个元素最多入队和出队一次。
• 空间复杂度：O(k) 队列最多存储 k 个元素。

优化方案2：分块预处理（空间换时间）

将数组分成大小为 k 的块，预处理每个块的 前缀最大值 和 后缀最大值，利用二者快速计算窗口最大值。

public class Solution {public int[] maxSlidingWindow(int[] nums, int k) {if (nums.length == 0) return new int[0];int n = nums.length;int[] prefixMax = new int[n];int[] suffixMax = new int[n];// 计算前缀最大值for (int i = 0; i < n; i++) {prefixMax[i] = (i % k == 0) ? nums[i] : Math.max(prefixMax[i - 1], nums[i]);}// 计算后缀最大值suffixMax[n - 1] = nums[n - 1];for (int i = n - 2; i >= 0; i--) {suffixMax[i] = ((i + 1) % k == 0) ? nums[i] : Math.max(suffixMax[i + 1], nums[i]);}// 计算每个窗口最大值int[] result = new int[n - k + 1];for (int i = 0; i <= n - k; i++) {result[i] = Math.max(suffixMax[i], prefixMax[i + k - 1]);}return result;}
}

核心逻辑

1. 前缀最大值： prefixMax[i] = 从块起点到 i 的最大值。
2. 后缀最大值： suffixMax[i] = 从 i 到块终点的最大值。
3. 窗口最大值： 设窗口为 [i, j]（j = i + k - 1），则最大值 = max(suffixMax[i], prefixMax[j])。

复杂度分析

• 时间复杂度：O(n) 预处理和计算结果各需遍历一次数组。
• 空间复杂度：O(n) 需额外存储前缀和后缀最大值数组。

总结

方法	时间复杂度	空间复杂度	核心优势
优先队列（修正）	O(n log n)	O(n)	逻辑简单，易实现
单调队列	O(n)	O(k)	最优效率，推荐使用
分块预处理	O(n)	O(n)	无队列操作，适合并行计算

推荐实现：单调队列法在性能和代码简洁性上达到最佳平衡，是解决滑动窗口最大值问题的首选方案。