算法题（221）：多重背包（二）

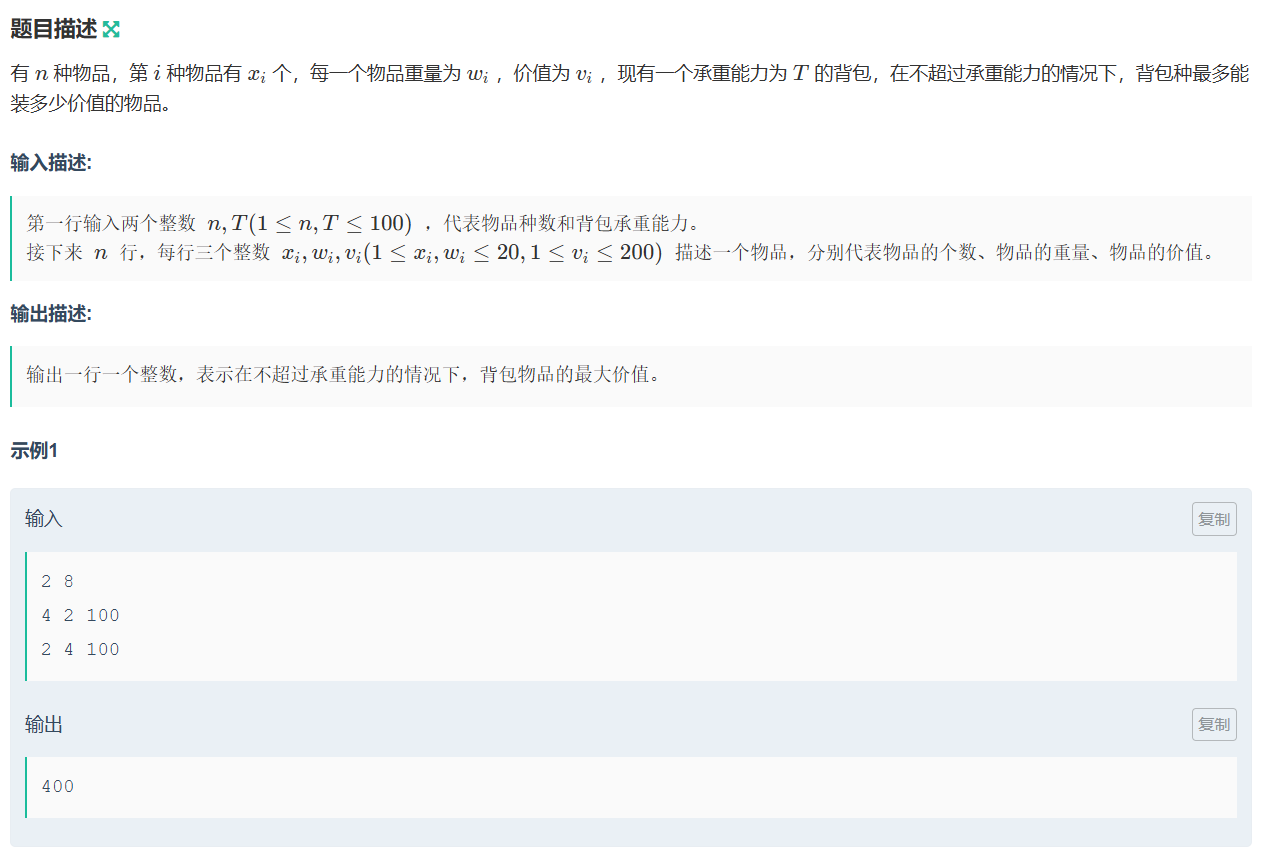
审题：
本题解是基于已经用非空间优化解决了该题的前提下，讲解空间优化方法

算法题（220）：多重背包（一）-CSDN博客

思路：
方法一：动态规划+二进制空间优化

多重背包的二进制空间优化本质：

将每一种物品都利用二进制一分为n，从而让每一种“新物品”都只有一份，构建出新的物品w与v数组后利用01背包解题，从而优化第三层循环

（O（n）->  O（logn））

图示：
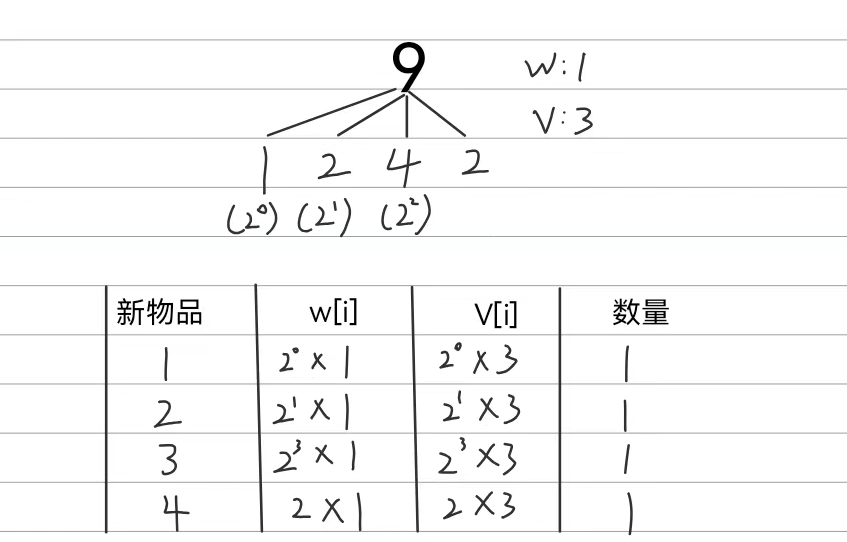
我们以数量为9，重量为1，价值为3的多重背包中的一种物品为例，讲解如何利用二进制的方法优化

9个原品种物品，通过二进制划分，分为了四种数量为1的新物品

我们利用二进制的每个位的数将原数量分解为若干堆，每堆都是包含任意个i品种物品的“新物品”，然后我们将“新物品”的价值和重量都计算出来，那么问题就转换为01背包问题了

注意：

1.我们进行二进制划分的时候不可能所有的数都可以刚好划分完，最后剩下的数量就可以分为新的一种物品

2.本优化方法无法适用于求方案数的题目，因为这种方法会凭空产生更多品种物品，从而让原本只有一种的方案变为多种

eg：f[4][3]，我们要求在前四种物品中，保证载重小于3的前提下，所有选择方案数

若使用二进制优化，我们可以选择新物品1与2，或者新物品1与4这两种方案

可是对于实际情况来说，这两种选择都是对原物品选择3份，只能算一种方案，故优化后的方案数会增多

解题：
 

#include<iostream>
using namespace std;
const int N = 110*5;
int n,m,pos;
int w[N],v[N];
int f[N];
int main()
{cin >> n >> m;for(int i = 1; i <= n; i++){int x,y,z;cin >> x >> y >> z;//二进制优化-》01背包int num = 1;while(x >= num){pos++;w[pos] = num * y;v[pos] = num * z;x -= num;num *= 2;}if(x != 0)//处理剩余数量{pos++;w[pos] = x*y;v[pos] = x*z;}}//01背包解决问题for(int i = 1; i <= pos; i++){for(int j = m; j >= w[i]; j--){f[j] = max(f[j],f[j-w[i]]+v[i]);}}//答案输出cout << f[m] << endl;return 0;
}

注意：

1.N的取值，由于物品数量的最大值为20，而20最多可以分为5种新物品，所以最多产生的新物品数量就等于物品种类最大值*5

多重背包