归并排序、计数排序以及各种排序稳定性总结

归并排序 
1.基本思想：
归并排序（MERGE - SORT）是建立在归并操作上的一种有效的排序算法, 该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 

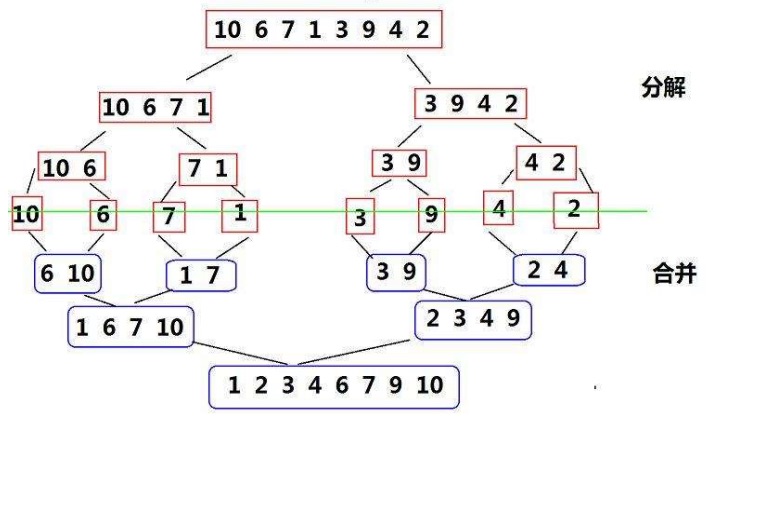
2.归并排序的实现(升序）
思路：两个有序区间的归并，依次进行比较，然后将小的插入到新的空间，但是先要让两个区间有序(递归）
1.递归版归并排序

  

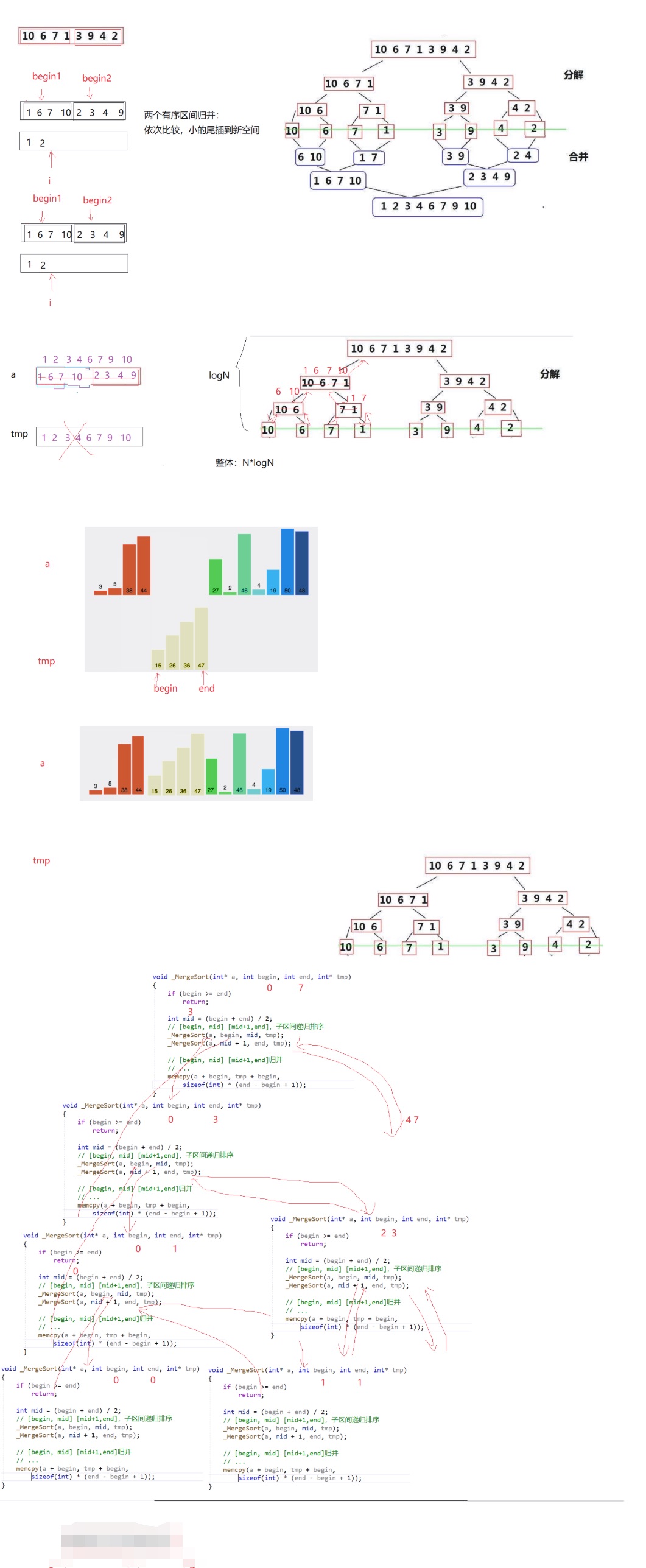
测试

 

递归代码

 

2.非递归版归并排序(不能使用栈）

思路：（画图）

 

测试：

 

非递归代码

 

3.归并排序的特性总结： 
1. 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度：O(N * logN)
3. 空间复杂度：O(N)
4. 稳定性：稳定

4.归并排序性能测试

 

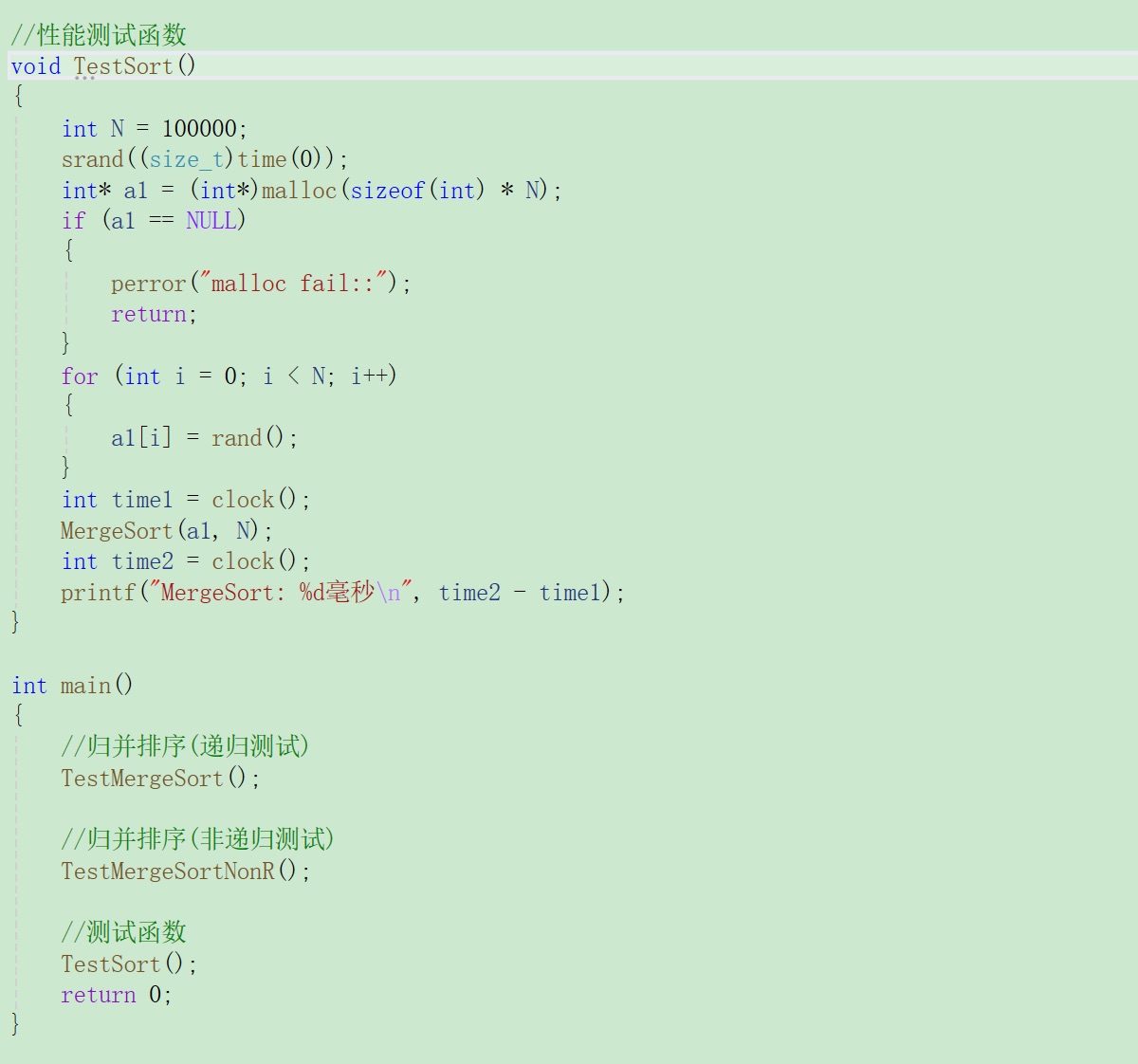
非比较排序 
思想：计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。 操作步骤：
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中

非比较排序有基数排序、计数排序、桶排序等

计数排序：
思路：
1.统计每个数据出现的次数
2.排序：遍历一遍计数的数组，然后对着原数组进行从小到大按个数填充。每个数是几个就在原数组后依次写几个

 

计数排序的特性总结： 
1. 计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
2. 时间复杂度：O(N + range)
3. 空间复杂度：O(范围)
4. 稳定性：稳定
5.计数排序适合范围集中，且范围不大的整型数组排序，不适合范围分散或非整形的排序，如字符串、浮点数等

代码

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i] = r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的
综上所述，稳定性也就是相同数据的相对位置在排序后是否改变，不变就是稳定的，否则就是不稳定的

1.稳定的排序：冒泡排序、插入排序、归并排序
2.不稳定的排序：选择排序、希尔排序、堆排序

 

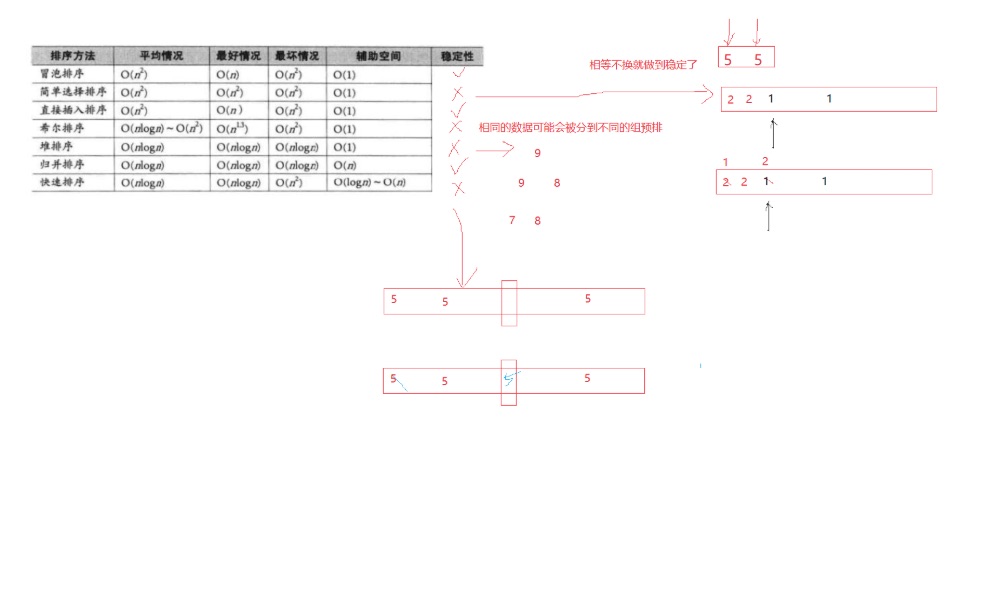
注：
选择排序不稳定，比如2  2  1  1在排序时，交换第一个1和第一个2时，就让2不稳定了