第三章 鸽巢原理

简单形式

简单的来说就是两个几何的映射无法做到一一对应就可能导致鸽巢原理。

应用

这里的要点为序列的联系子集可以看成两个从a1开始的序列的差：

由题目条件得知：我们需要求两个从a1开始的连续序列除以m有相同的余数
然后在这个新的问题中也是假设不能有余数为0的，因此，余数的个数少于总情况数，可以使用鸽巢原理。

由上题得知，还是要转化为两个连续序列的差。而这两个连续序列满足的条件为$a_i=a_j+21$，由此构造一个新的序列（包含a$a_i+21$的序列），在这个序列中用鸽巢原理。

此题关键是要知道整数的表达形式，这样应该可以解决所有的两数整除问题。

这里首先列出了余a所有情况，然后证明了其除以n的余数各不相同。、

加强版

加强版是在简单形式的基础上对每个鸽巢的鸽子数提出了要求。

由此我们得出了结论：鸽巢原理本质是求最高的下限，因此我们总是要平均情况（最不极端的分配情况）

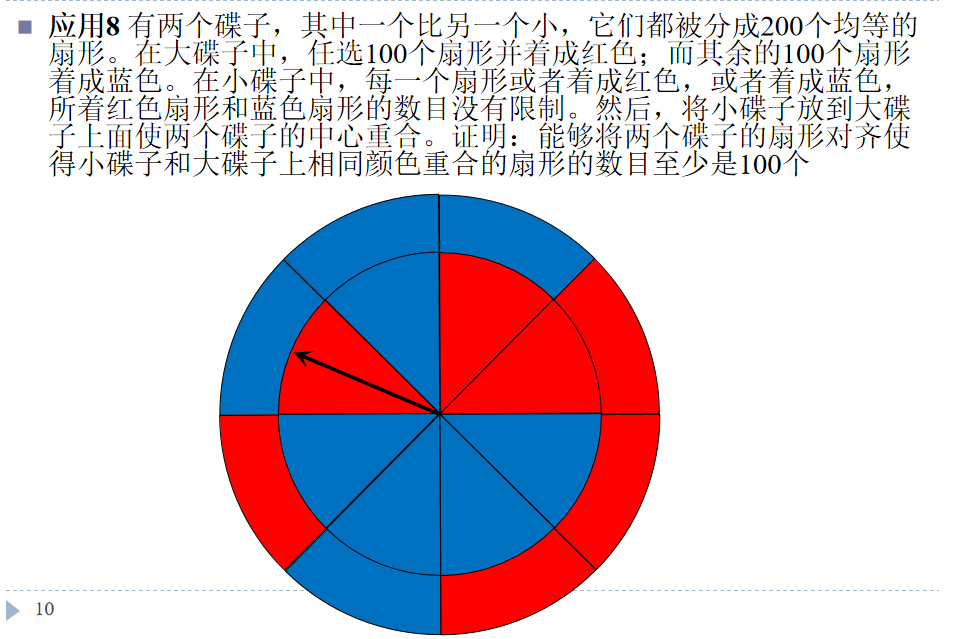
题干解析：这里说的意思其实是，任意一种小盘子，总能找到一种摆放方式，使得相同颜色的扇形至少为100.
关键点：这题其实可以算出无论是什么小盘子，其所有摆放的重合颜色总数是一样的，都是20000种，而一共有200种摆放方式，则可有平均值定理证明。

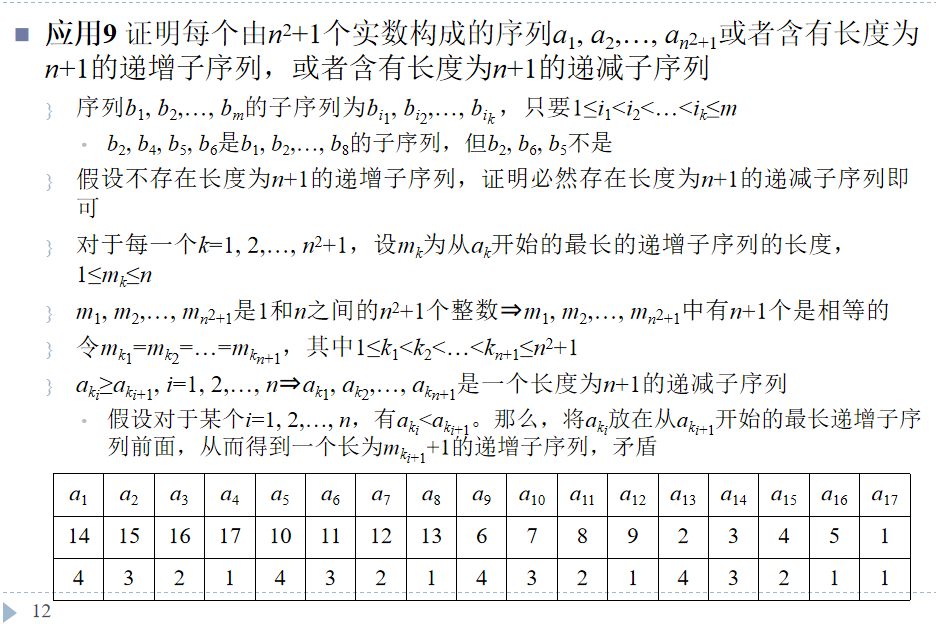
思路说明：假设不存在n +1递增子序列的情况，证明递减。
将整体分为每组n个的递增数列，结果会出现n + 1.
然后再证明这n + 1的情况必然是递减即可。

Ramsey定理

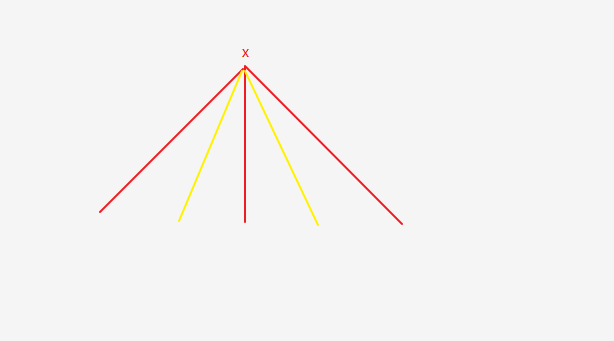
证明方法如上图所示，K6中，每个结点都有5条边，对于二着色来说，必定会有三条边着同一颜色。如上图设定是着红色。如果三条红边两两相邻均是黄边，则有一个单色三角形；若有一条红遍，也会和过x的红边组成三角形。

更一般的Ramsey定理

对于这一步进行说明：
|Rx|+|Bx|=p-1=r(m-1, n)+r(m, n-1)-1⇒|Rx|≥r(m-1, n)或者|Bx|≥ r(m, n-1)假设|Rx|≥r(m-1, n)成立。
其实和简单，假设这两个条件同时不成立就能明白了。
最后证明的这个不等式实际就证明了存在上界，然后这种数本来就存在下界，这样就证明了其存在。