数据结构_ 二叉树线索化：从原理到手撕实现

概念

二叉树线索化是一种对二叉树结构的优化技术，目的是利用二叉树中闲置的空指针（即左右孩子为空的指针），存储节点在某种遍历顺序（如中序、前序、后序）中的前驱或后继节点信息，从而实现二叉树的高效遍历（无需递归或栈）。

为什么需要线索化？

普通二叉树的遍历（如中序、前序）通常依赖递归或栈来记录节点的前驱 / 后继关系，但存在两个问题：
空指针浪费：对于一个有 n 个节点的二叉树，有 n+1 个空指针（每个节点有 2 个指针，共 2n 个，实际使用 n-1 个指向孩子，剩余 2n - (n-1) = n+1 个为空）。
遍历效率低：递归需要栈空间，迭代需要手动维护栈，且无法直接通过节点找到其前驱 / 后继。
线索化通过利用这些空指针存储 “线索”（指向前驱或后继的指针），解决了上述问题。

核心概念

线索：将二叉树中原本为空的左 / 右指针，改为指向该节点在某种遍历顺序中的前驱节点（左线索）或后继节点（右线索）。
标志位（tag）：为了区分指针是指向孩子（真实指针）还是指向线索（前驱 / 后继），每个节点会增加两个标志位：
ltag：左标志位，0 表示左指针指向左孩子（真实指针），1 表示左指针是左线索（指向前驱）。
rtag：右标志位，0 表示右指针指向右孩子（真实指针），1 表示右指针是右线索（指向后继）。

结构定义

typedef struct Node {int val;          // 节点值int ltag, rtag;   // 0：真实孩子，1：线索struct Node *lchild, *rchild;  // 左/右指针（可能是孩子或线索）
} Node;

本篇我们详细的探讨中序线索化二叉树：按中序遍历（左→根→右）规则，为每个节点添加前驱（左线索）和后继（右线索）。

手撕中序线索化二叉树

通过二叉树文章可以知道，二叉树的基本操作，初始化一个结点，插入二叉树，销毁二叉树

二叉树的定义

这里就不再过多赘述了，需要注意的是，在线索化二叉树时，加入了ltag，rtag两个标志位，所以，在前中后序遍历的时候需要走真实路径，也就是 ltag = 0 , rtag = 0 的情况

所以在遍历的时候代码应该为：

//前序遍历
void pre_order(Node* root) {if (root == NULL)return;printf("%d ", root->val);if(root->ltag==0)pre_order(root->lchild);if (root->rtag == 0)pre_order(root->rchild);return;
}
//中序遍历
void mid_order(Node* root) {if (root == NULL)return;if (root->ltag == 0)mid_order(root->lchild);printf("%d ", root->val);if (root->rtag == 0)mid_order(root->rchild);return;
}
//后序遍历
void back_order(Node* root) {if (root == NULL)return;if (root->ltag == 0)back_order(root->lchild);if (root->rtag == 0)back_order(root->rchild);printf("%d ", root->val);return;
}

如何构建线索二叉树(原理)

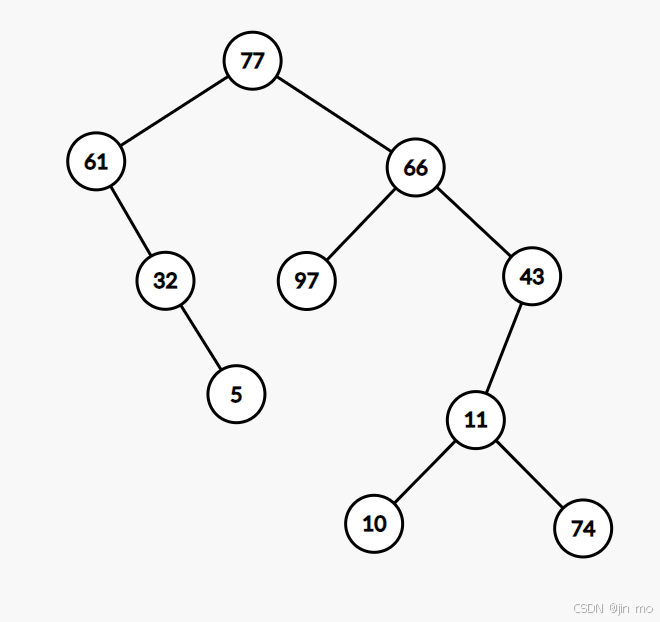
我们以这个树结构为例子

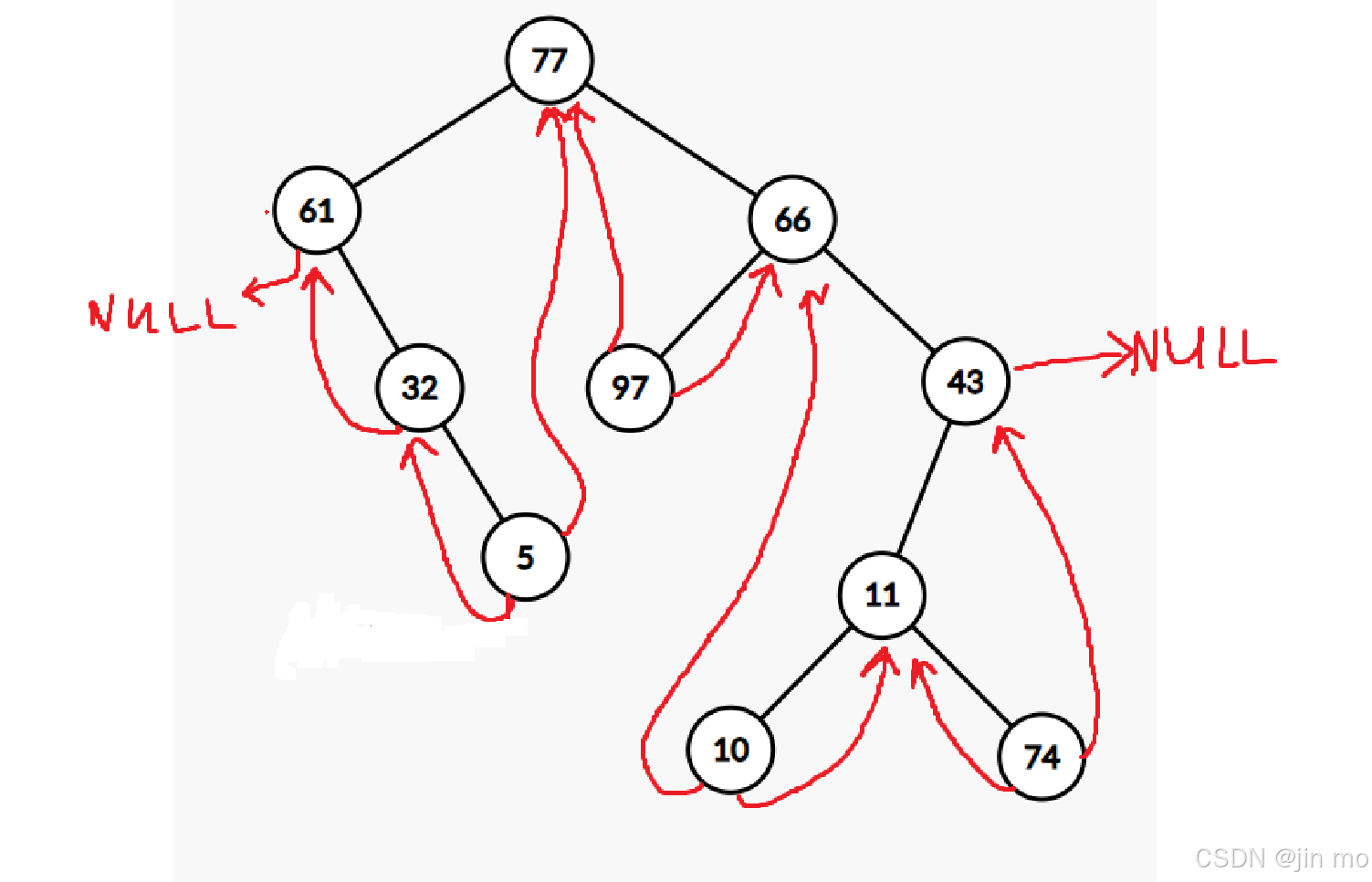
根据概念：将二叉树中原本为空的左 / 右指针，改为指向该节点在某种遍历顺序中的前驱节点（左线索）或后继节点（右线索）。
分别站在每个结点上分析一下：
中序遍历：61 32 5 77 97 66 10 11 74 43 .

节点 61：

• 左孩子为空 → 左线索指向 NULL（因为是中序遍历的第一个节点，无前驱），ltag=1。
• 右孩子存在（32，真实子节点） → rtag=0，右指针仍指向 32。
  节点 32：
• 左孩子为空 → 左线索指向前驱 61，ltag=1。
• 右孩子存在（5，真实子节点） → rtag=0，右指针仍指向 5。
  节点 5：
• 左孩子为空 → 左线索指向前驱 32，ltag=1。
• 右孩子为空 → 右线索指向后继 77，rtag=1。
  节点 77：
• 左孩子存在（61，真实子节点） → ltag=0，左指针仍指向 61。
• 右孩子存在（66，真实子节点） → rtag=0，右指针仍指向 66。
  节点 97：
• 左孩子为空 → 左线索指向前驱 77，ltag=1。
• 右孩子为空 → 右线索指向后继 66，rtag=1。
  节点 66：
• 左孩子存在（97，真实子节点） → ltag=0，左指针仍指向 97。
• 右孩子存在（43，真实子节点） → rtag=0，右指针仍指向 43。
  节点 10：
• 左孩子为空 → 左线索指向前驱 66（因为 10 的前一个节点是 66），ltag=1。
• 右孩子为空 → 右线索指向后继 11，rtag=1。
  节点 11：
• 左孩子存在（10，真实子节点） → ltag=0，左指针仍指向 10。
• 右孩子存在（74，真实子节点） → rtag=0，右指针仍指向 74。
  节点 74：
• 左孩子为空 → 左线索指向前驱 11，ltag=1。
• 右孩子为空 → 右线索指向后继 43，rtag=1。
  节点 43：
• 左孩子存在（11，真实子节点） → ltag=0，左指针仍指向 11。
• 右孩子为空 → 右线索指向 NULL（因为是中序遍历的最后一个节点，无后继），rtag=1。

代码实现及其原理

在构建二叉树线索化时，最重要的就是build_midTreeThread()这个函数

Node* prenode = NULL,*midorder=NULL;
void build_midTreeThread(Node* root) {if (root == NULL) return;if (root->ltag == 0) build_midTreeThread(root->lchild);if (midorder == NULL) midorder = root;if (root->lchild == NULL) {root->lchild = prenode;root->ltag = 1;}if (prenode && prenode->rchild == NULL) {prenode->rchild = root;prenode->rtag = 1;}prenode = root;if (root->rtag == 0) build_midTreeThread(root->rchild);return;
}

手撕递归与线索化

这个函数设计的巧妙之处，在于记录前一个结点prenode（midorder后面会讲到，这里理解为这个二叉树第一次遍历到的点），这样一旦发现当前结点左孩子为NULL就可以直接指向pernode，来完成前驱这一步，但是这里难得点还是在于递归所以，这里着重带着大家分析一下这里是如何递归的（看着上面的图食用更佳哦）。
进入构建函数：

可以看到，初始化的prenode和第一个中序遍历得到的节点都为NULL，第一个结点的val=77,准备递归
代码走到这一步，代表现在进入了 77的左子树，的最左边的结点

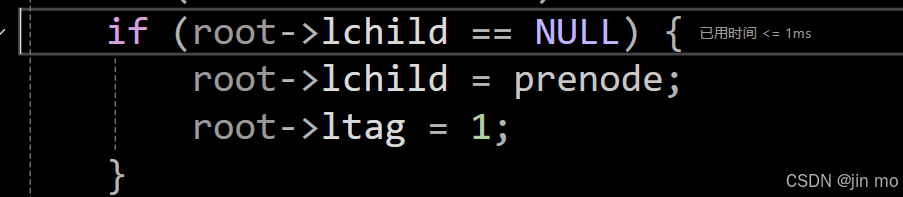
也就是 61 ，可以看到，跟上面的图是一致的，61这个结点左孩子为NULL，右孩子为右子树，这里我们要开始构建第一个线索化，也就是将 61 的前驱（lchild）记为NULL

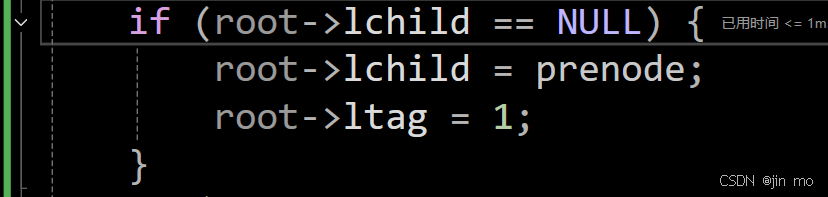
代码进入到这一步，将prenode(NULL)的值赋给61的左孩子，将ltag更改为1，代表这是一条线索化

prenode为NULL，不执行此语句

最后更新prenode为 61

当代码执行到这一步时，代表要进入 61 的右子树

又开始递归进入左子树，由于32没有左子树，所以进入线索化


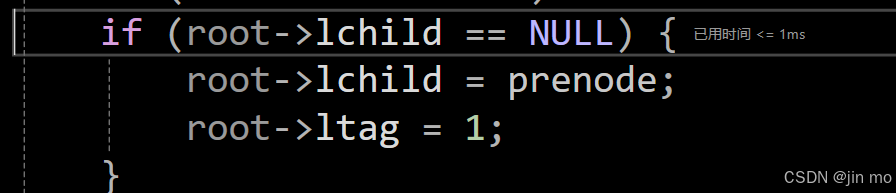
将root(32)做线索化处理，左孩子指向prenode（61）
由于prenode(61)存在右子树,所以不做线索化处理,进入root(32)的右子树

此时root=5做线索化处理，左孩子指向prenode（32）

走到 5 时代表 32 的右子树走完了，回到32，继续回到61，最终回到77


由此可见，线索化成功
当结点回到77的时候，代表77的左子树已经全部线索化完毕，但是需要注意的是，此时prenode还在5这个结点，最终 5 指向此时root(77)，也就是5的后继


更新完毕，准备进入77右子树的递归

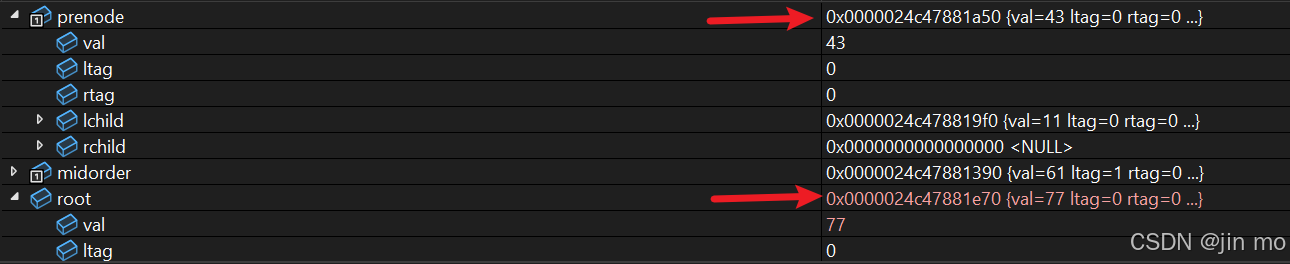
与 77 的左子树相同，同样会先递归到最左边的元素，也就是77中序遍历第一次在右子树中访问到的元素 97


由于root(97)的左孩子为NULL，将其线索化指向prenode(77)
回溯到结点 66


prenode的右孩子也为NULL

对其线索化，指向root(66)

成功线索化97结点的前驱与后继

进入66的右子树，依旧重复，先递归到66右子树的最左边（最先访问到的值）10


左孩子为NULL，指向prenode(66)
回溯root=11,prenode(10)

prenode(10)的右孩子为NULL，对其线索化指向root(11)

递归进入11的右子树 74

74的左孩子为NULL，对其线索化指向prenode(11)
最终回到43

prenode(74)
右孩子为NULL，对其线索化指向root(43)

最后更新prenode为43，回溯到77，递归完成

最后再封装一个函数，将43的右孩子指向NULL即可：

void __build_midTreeThread(Node * root) {build_midTreeThread(root);prenode->rchild = NULL;prenode->rtag = 1;return;
}

手撕线索化遍历

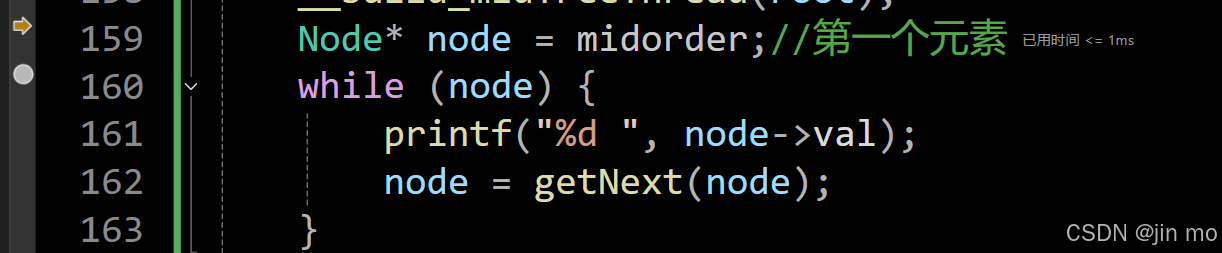
Node* node = midorder;//第一个元素

这里我们就用上了之前设置的midorder这个变量，记录了第一个线索化的值，我们从这个值开始，根据线索对这个二叉树进行遍历
这里的遍历和遍历链表很类似，都是获取到下一个结点，依次遍历，那么我们的重点就是在这个getNext()函数了

	while (node) {printf("%d ", node->val);node = getNext(node);}

Node* getNext(Node* node) {if (node->rtag == 1) {return node->rchild;}node = node->rchild;while (node->lchild && node->ltag == 0) node = node->lchild;return node;
}

当一个结点拥有线索化(l/rtag=1)时，直接返回其后的线索
如果没有线索化，根据中序遍历的特性： 左 根 右，当前结点的后继结点必然为右子树中的最左侧的结点
得出：

	node = node->rchild;  // 进入右子树// 循环找到右子树中最左侧的节点（左指针为真实子树时继续向左）while (node != NULL && node->ltag == 0 && node->lchild != NULL) {node = node->lchild;}

例如，61 没有rchild线索化，那么就进61的右子树查看，node此时为32，32没有左孩子，所以循环直接跳过，返回32


依次重复，直至到 5 这个结点，进入getNext(5),此时由于5有rchild的后继线索，直接返回77

77进入getNext();获取其右子树 66 ，一直遍历66的左子树部分，得到97，97的拥有rchild线索，得到66，没有线索，得到其右子树43，进入43，再继续遍历43的左子树部分，得到10,10拥有rchild线索,得到11，11没有线索，得到11的右子树74,没有左子树，直接返回，74拥有线索化43，最后直接得到43，至此，线索化遍历完毕

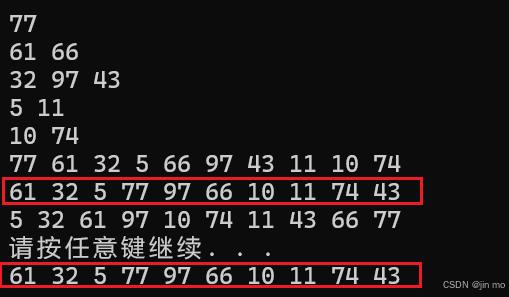
利用递归和线索化遍历结果相同，中序线索化完毕（遍历时无需递归或栈）

总结

中序线索化二叉树通过利用空指针存储遍历顺序信息，实现了：

• 空间优化：利用n+1个空指针
• 遍历效率：O(n)时间复杂度，O(1)空间复杂度
• 无需递归栈：线性遍历整个二叉树

适用于需要频繁进行中序遍历且对空间效率要求较高的场景。