二维数组前缀和
目录
一:题目链接
二:题目思路
如何初始化二维数组 dp 。
如何取得 dp 数组对应下标的值
三:代码实现
一:题目链接
二:题目思路
首先,我们最先想到的肯定是模拟实现来解决这道题,就是给出什么,我就求的一次答案,但是,题目给出查询次数多了,每次都暴力模拟,这样的方式肯定是超时了,所以要另想他法。
有一种前缀和的算法思想,对于这道题目来说,就是创建一个二维数组 dp ,dp 每一个元素大小代表 以原二维数组从 [ 1 , 1 ] 作为左上角,以原二维数组 [ (当前下标) , (当前下标) ] 作为右下角组成的矩形区间所有元素的总和。
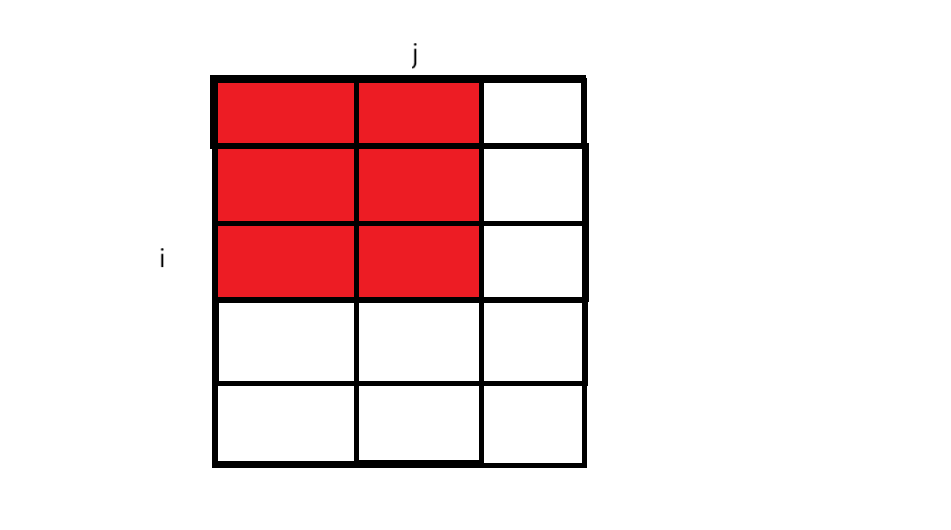
假设原二维数组如上图,如果当前二维数组 dp 的下标是 [ i ][ j ] ,那么 dp[ i ][ j ] = “原二维数组红色区域元素和”。
如何初始化二维数组 dp 。
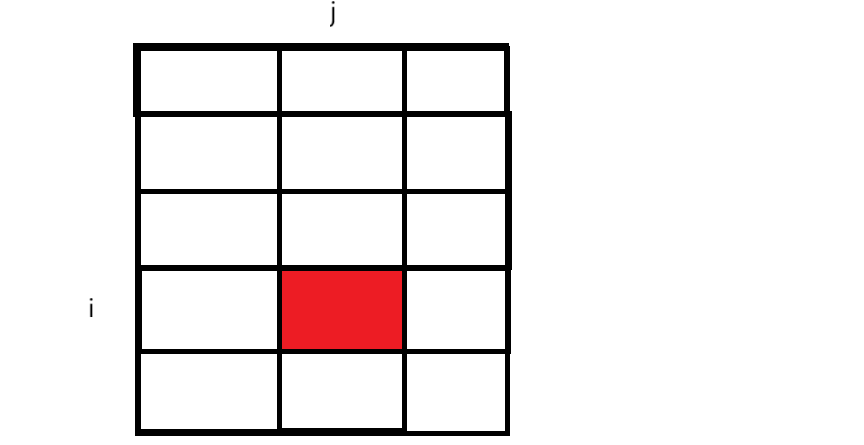
上图红色区域是我们要初始化 dp 的下标元素,假设原二维数组是 arr ,我们可以用公式:
dp[ i ][ j ] = arr[ i ][ j ] + dp[ i - 1 ][ j ] + dp[ i ][ j - 1 ] - dp[ i - 1 ][ j - 1 ],因为多加了一个蓝色区域元素,所以最后减去一个蓝色区域:
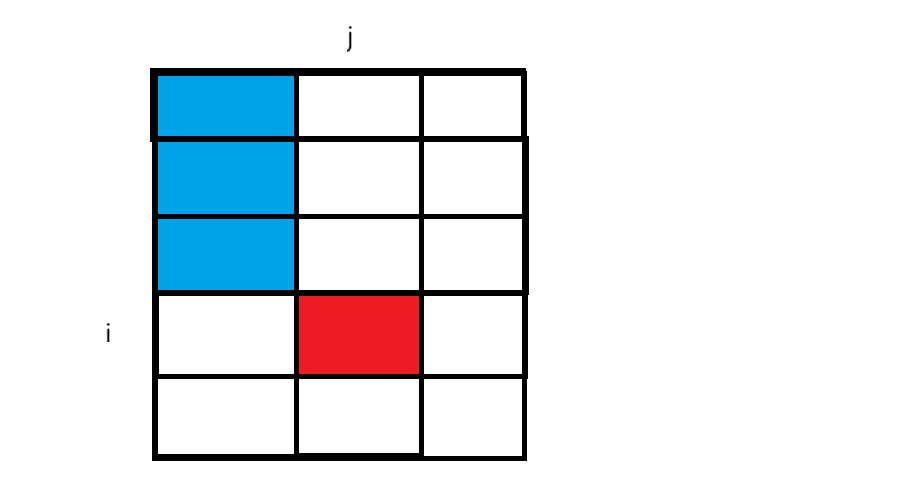
如何取得 dp 数组对应下标的值
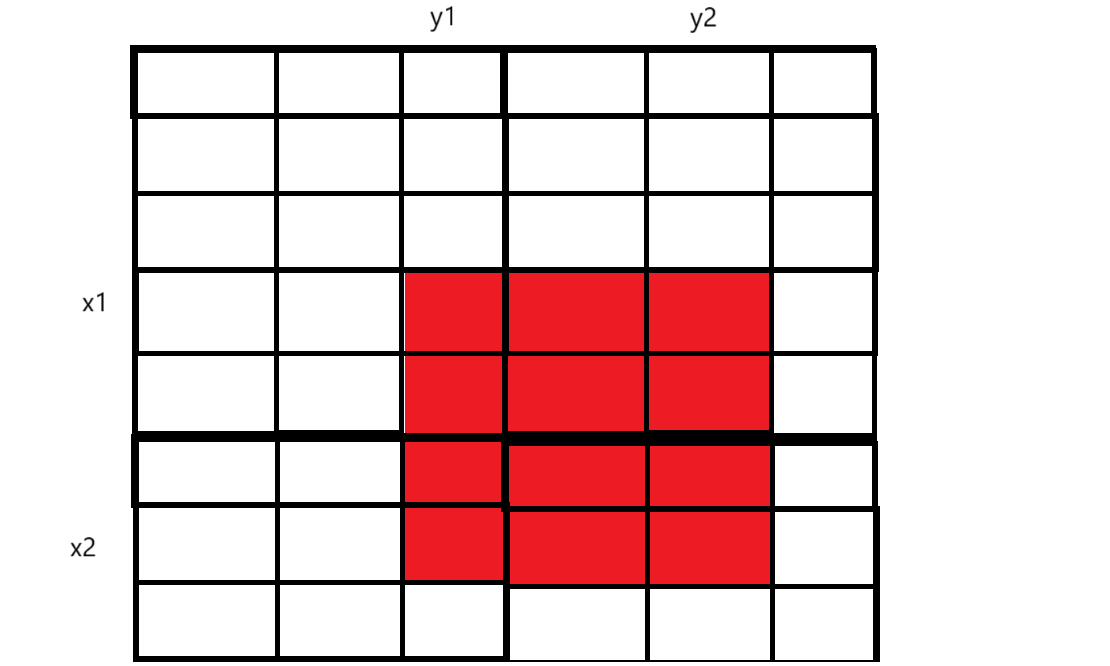
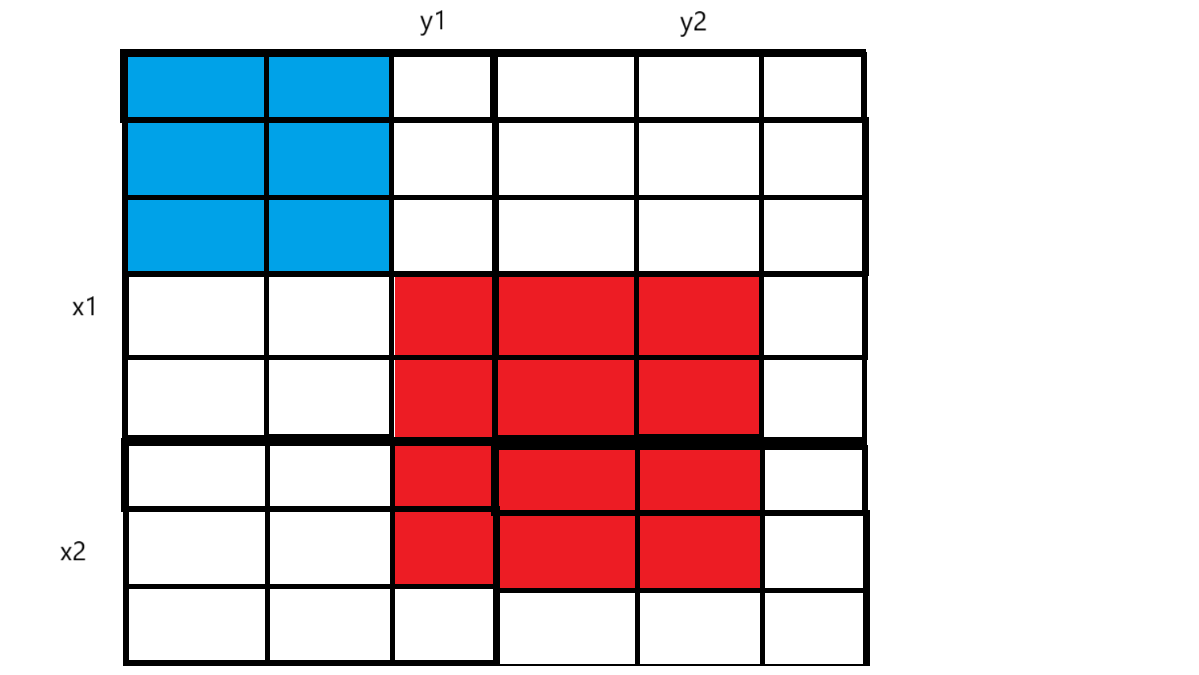
如上图,红色区域是我们所需的元素总和,利用之前初始化完成的二维数组 dp ,利用公式即可求得我们所需的: dp[ x2 ][ y2 ] - dp[ x2 ][ y1 - 1 ] - dp[ x1 - 1 ][ y2 ] + dp[ x1 - 1 ][ y1 - 1 ] ,因为多减了一个 蓝色区域,所以要加上一个蓝色区域:
三:代码实现
Scanner in = new Scanner(System.in);int n = in.nextInt();int m = in.nextInt();int q = in.nextInt();//原二维数组int[][] arr = new int[n + 1][m + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {arr[i][j] = in.nextInt();}}//初始化前缀和数组 dp long[][] dp = new long[n + 1][m + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {dp[i][j] = arr[i][j] + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];}}while (q > 0) {int i = 0;int x1 = in.nextInt();int y1 = in.nextInt();int x2 = in.nextInt();int y2 = in.nextInt();System.out.println(dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1]);q--;}