Python 数学公式构建海洋不明生物（好像是水母）动画 - 波浪起伏效果

Python 数学公式构建海洋不明生物（好像是水母）动画 - 波浪起伏效果

flyfish

Python 数学公式构建海洋不明生物（好像是水母）动画 - 简谐振动
效果展示与源码

可以先欣赏下海洋不明生物（好像是水母）的动画

代码绘制效果如下图

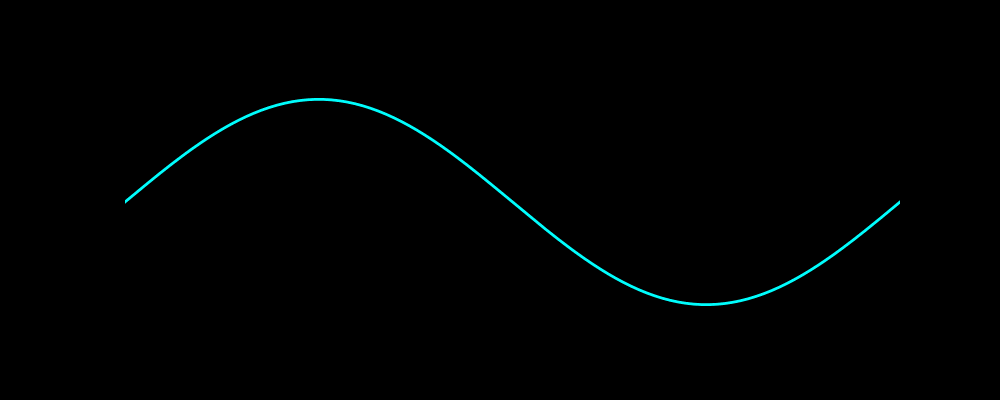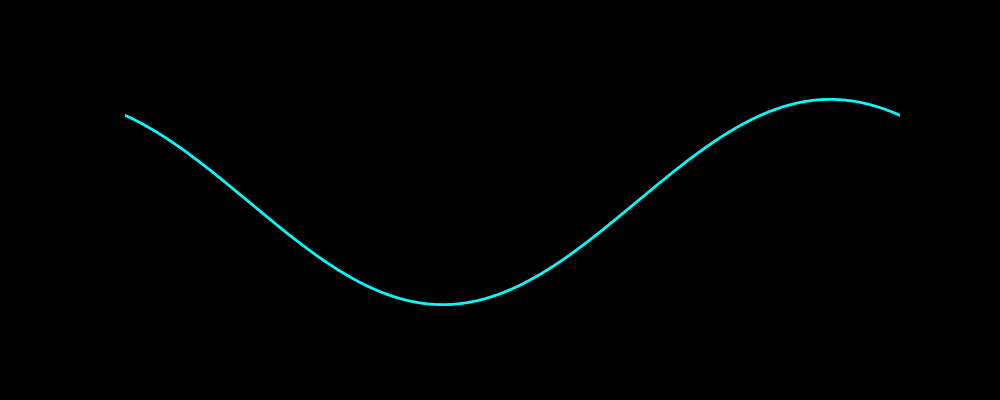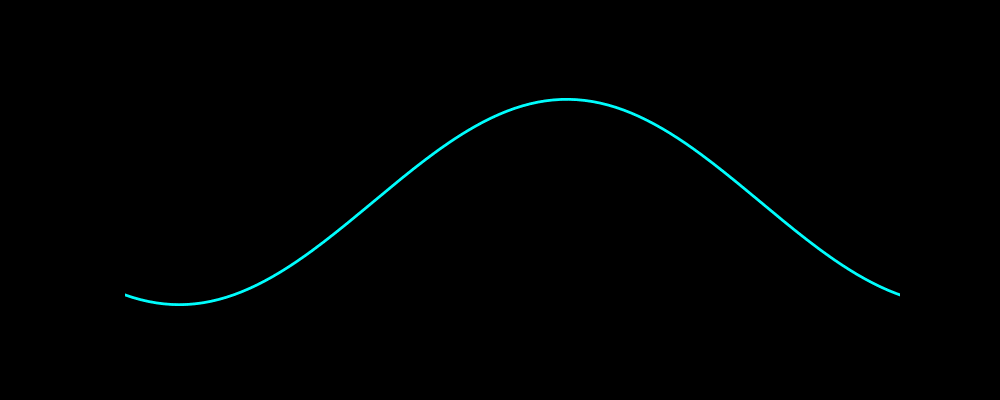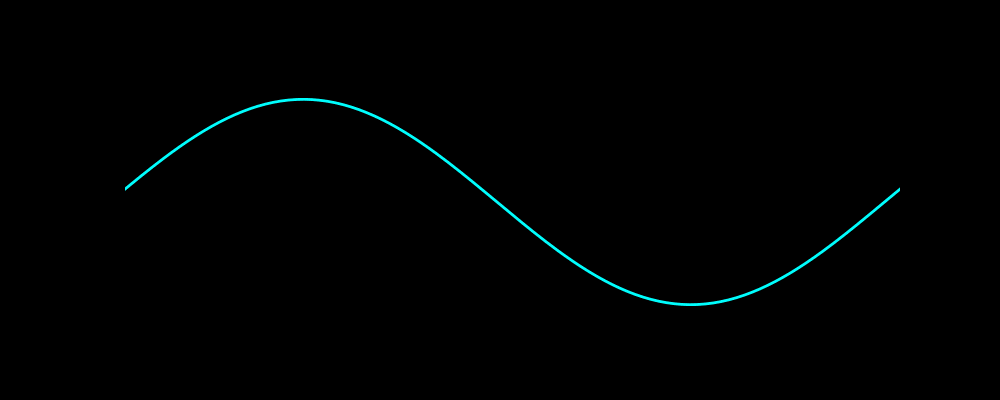
一、波

波浪起伏效果的本质是基于波的传播原理，尤其是对简谐波（harmonic waves） 的数学模拟。自然界中的水面波动、海浪起伏是无数介质粒子（如水分子）在局部做简谐振动，并通过介质传递能量形成的集体运动。

1. 简谐振动回顾

简谐振动是单个粒子（如水分子）的周期性往复运动，其位移随时间的变化遵循正弦函数规律，是构成波动的“基本单元”。

（1）核心公式

单个粒子的位移函数为：
$x(t)=A\sin (\omega t+\varphi )$

（2）参数解析

• $A$：振幅（Amplitude），粒子偏离平衡位置的最大距离，决定振动的“强度”。
• $\omega$：角频率（Angular Frequency），与频率$f$的关系为$\omega =2\pi f$，决定振动的“快慢”（$f$单位为Hz，即每秒振动次数）。
• $t$：时间（Time），振动随时间演化变量。
• $\varphi$：相位（Phase），初始时刻的角度偏移（取值范围$0$~$2\pi$），决定振动的“起始状态”。

（3）物理原理

简谐振动的产生源于线性恢复力，即恢复力与位移成正比且方向相反，遵循胡克定律：
$F=-kx$

根据牛顿第二定律（$F=ma$），可推导加速度与位移的关系：
$a=-\frac{k}{m}x$

该微分方程的解即为正弦函数形式，体现了“偏离平衡位置越远，恢复力越强”的特性。振动过程中，粒子的动能与势能相互转换，总能量守恒（理想无阻尼情况下），因此可维持周期性运动。

2. 波的形成

波动并非孤立粒子的振动，而是相邻粒子通过介质（如水）传递能量，形成的“空间协调的集体运动”。

（1）形成逻辑

1. 单个粒子的振动：以水面上某一点为例，它仅在垂直方向做简谐振动，位移随时间变化为：
   $y(t)=A\sin (\omega t)$
2. 粒子间的能量传递：当该粒子振动时，会通过水的张力“拉动”相邻粒子运动，但相邻粒子的振动存在时间延迟（能量传递需要时间）。
3. 空间波形的形成：随着延迟的累积，多个粒子的振动在空间上形成连续的“峰-谷”结构，即波形；能量沿传播方向传递，形成波动。

（2）波类型

根据波形是否移动，可分为两类基础波动：

• 行波（Traveling Wave）：波形随时间沿传播方向移动，能量同步传递，如海浪、声波。代码中实现的正是行波效果。
• 驻波（Standing Wave）：波形固定在空间中振荡，不随时间移动，能量不传递，如吉他弦振动、封闭管道中的声波（可通过两个反向传播的行波叠加实现）。

（3）波动方程

所有线性波动均满足波动方程，该方程描述了位移随时间和空间的变化关系：
$\frac{{\partial }^{2}y}{\partial t^2}=v^2\frac{{\partial }^{2}y}{\partial x^2}$

其中，$v$为波速（取决于介质特性，如水的密度、表面张力等），该方程的通解即为行波或驻波的数学表达式。

3. 行波公式

代码实现波浪效果是行波的数学模型，它融合了“时间演化”与“空间分布”，准确描述波形的传播过程。

（1）核心波函数

行波的位移函数同时依赖空间位置$x$和时间$t$，表达式为：
$y(x,t)=A\sin (kx-\omega t+\varphi )$

（2）参数解析

参数符号	名称	物理含义与代码关联
$A$	振幅	对应代码中的amplitude，控制波峰与波谷的高度差。
$k$	波数	$k=\frac{2\pi }{\lambda }$（$\lambda$为波长），波数越大，波长越短；代码中通过frequency间接控制（频率越高，波数越大）。
$x$	空间位置	波形在水平方向的坐标，对应代码中固定的空间数组。
$\omega$	角频率	$\omega =2\pi f$，控制粒子振动速度，与波的传播节奏相关。
$t$	时间	对应代码中随帧累积的时间变量，驱动波形动态传播。
$-\omega t$	传播方向项	负号表示波形沿$x$轴正方向传播（若改为$+\omega t$，则沿负方向传播）。
$\varphi$	初始相位	控制波形的初始位置，代码中可添加随机性避免波形单调。

（3）推导与关系

• 波速与频率、波长的关系：波速$v$是波形移动的速度，满足$v=\frac{\omega }{k}=\lambda f$，代码中通过wave_speed参数缩放时间变量$t$，直接控制波的传播速度。
• 从简谐振动到行波：行波公式可理解为“空间上的简谐振动叠加”——每个空间位置$x$处的粒子都在做简谐振动（$\sin (-\omega t+(kx+\varphi ))$），但不同位置的相位差为$kx$，因此形成连续的空间波形。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation, PillowWriter# 参数设置（可调整）
amplitude = 1.0      # 振幅（波浪高度）
frequency = 1.0      # 频率（波浪密集度）
wave_speed = 2.0     # 波速（传播速度）
num_points = 200     # x轴点数（分辨率）
animation_frames = 100  # 动画帧数
interval = 50        # 每帧间隔（ms）# 创建图形
fig, ax = plt.subplots(figsize=(10, 4), facecolor='black')
ax.set_facecolor('black')
ax.set_xlim(0, 2 * np.pi)
ax.set_ylim(-amplitude - 0.5, amplitude + 0.5)
ax.axis('off')  # 隐藏轴线，纯视觉效果# x 数据（固定）
x = np.linspace(0, 2 * np.pi, num_points)# 初始波浪数据（y = amplitude * sin(frequency * x)）
line, = ax.plot(x, amplitude * np.sin(frequency * x), color='cyan', lw=2)# 更新函数：每帧计算新波形（引入时间 t，实现行波）
def update(frame):t = frame * (2 * np.pi / animation_frames) * wave_speed  # 时间累积y = amplitude * np.sin(frequency * x - t)  # 行波公式：sin(kx - ωt)line.set_ydata(y)return line,# 创建动画
ani = FuncAnimation(fig, update, frames=animation_frames, interval=interval, blit=True)# 保存为 GIF（使用 PillowWriter）
writer = PillowWriter(fps=1000 / interval)
ani.save('wave_animation.gif', writer=writer, dpi=100)print("波浪动画已保存为 wave_animation.gif")
plt.close(fig)  # 关闭图形，释放资源

波浪起伏效果通过以下参数控制外观与动态

• amplitude：振幅，增大该值可使波浪的峰谷差更大（波浪更高）。
• frequency：频率，增大该值可使单位长度内的波峰/波谷数量更多（波浪更密集）。
• wave_speed：波速，增大该值可使波浪沿传播方向移动更快。

实现

（1）核心实现逻辑

1. 帧更新（Frame Update）：使用FuncAnimation函数，每间隔interval毫秒调用一次update函数，计算当前帧的波形数据（$y$坐标）。
2. 时间演化（Time Evolution）：定义时间变量$t=\text{frame}\times \text{step}$，其中frame为当前帧数，step为每帧的时间增量，模拟连续的时间流逝。
3. 效率优化：设置blit=True，仅更新画面中变化的部分（波形线条），而非重绘整个画布，大幅提升动画流畅度。

（2）视觉效果构建

• 波形呈现：通过matplotlib的plot函数绘制水平空间坐标$x$与动态垂直位移$y(x,t)$的关系，形成连续的波浪线条。
• 场景增强：采用黑色背景模拟“水体”环境，增强波形的视觉对比度，使起伏效果更明显。

（3）动画保存机制

• GIF格式：使用PillowWriter将帧序列编码为GIF文件，帧率设置为$\frac{1000}{\text{interval}}$（单位：fps），确保动画播放速度与计算速度匹配。

代码实现的是理想化的单频简谐波，而真实海浪等自然波动更为复杂。