当前位置：首页 > news >正文

Low-Overhead Sensing RS Design for Integrated Sensing and Communication (ISAC)

news 2025/9/28 8:32:41

摘要——感知与通信一体化 (ISAC) 是迈向第五代移动通信技术增强 (5G-Advanced) 和第六代移动通信技术 (6G) 最重要的研究课题之一。通过分析感知获得的测量结果，可以支持多样化的用例。测量需要参考信号 (RS)，其设计应旨在以低开销提供良好的感知性能。在 5G 新空口 (NR) 中为用户设备 (UE) 定位定义的定位参考信号 (PRS) 是一个很好的感知起点，其在估计精度和最大无模糊性能方面的表现已被验证是良好的。然而，NR PRS 的开销过高，限制了其在感知中的应用。

在本文中，受雷达系统中多重脉冲重复频率 (PRF) 方法的启发，我们提出了一种由具有互质梳齿尺寸（co-prime comb sizes）的多个梳状 RS 组成的新的感知 RS 模式。一方面，该梳状 RS 模式与通信系统具有良好的后向兼容性。另一方面，互质的梳齿尺寸可以有效消除由梳状 RS 模式引起的距离模糊。评估结果表明，所提出的感知 RS 模式可以达到与 NR PRS 相同的最大无模糊距离，但将开销从 7.14% 降低到了 2.21%。

索引术语——感知与通信一体化 (ISAC)，参考信号 (RS)，互质，梳状

文章目录

- I. INTRODUCTION
- II. SYSTEM MODEL AND DISTANCE AMBIGUITY
- - A. System model for sensing
  - B. Distance ambiguity and elimination method in radar
- III. ANALYSIS OF COMB RS AND NR PRS
- - A. Comb RS and sensing performance
  - B. NR PRS and sensing performance
- IV. PROPOSED SENSING RS
- - A. Proposed co-prime sensing RS pattern
  - B. Algorithm for co-prime sensing RS-based estimation

I. INTRODUCTION

最大无模糊性能和开销。在第一阶段，估计精度和分辨率是主要的研究焦点。现有的 5G 新空口 (NR) 中的 RS，如信道状态信息参考信号 (CSI-RS)、解调参考信号 (DMRS) 和定位参考信号 (PRS)，已被研究用于感知 [5] [6]。距离和速度的均方根误差 (RMSE) 结果显示了 NR RS 用于感知的可行性。然而，可能需要组合多个 NR RSs 来满足感知需求。

随着进一步的研究，最大无模糊性能以及开销成为感知 RS 设计的优化目标。在 [7] 中，研究了基于 PRS 的感知性能。结果显示了 PRS 在模糊函数以及距离和速度估计性能上的优越性。然而，NR PRS 所消耗的高开销限制了其使用。在 [8] 中，研究了感知 RS 的互质特性以增加最大无模糊距离和速度。在 [9] 中，提出了一种用于感知 RS 的多层结构化构造方法，并联合优化了峰旁比，该指标指示了最大无模糊性能和 RS 开销。然而，在 [8] [9] 中频域和时域上全新的非均匀 RS 模式设计与通常具有均匀模式的通信系统的 RS 不兼容。

在本文中，后向兼容性、开销和最大无模糊性能被共同考虑并设定为感知 RS 设计的研究目标。首先，为了良好的后向兼容性，我们提出了一种基于梳状 RS 模式的新型感知 RS。为了实现比 NR PRS 更低的开销，所提出的感知 RS 占用了更少的 OFDM 符号。为了在低开销下实现与 NR PRS 相同的最大无模糊距离，多个 OFDM 符号上的梳齿尺寸是互质的。分析和评估结果验证了在最大无模糊距离和开销方面的可行性和性能优越性。

在这里插入图片描述

II. SYSTEM MODEL AND DISTANCE AMBIGUITY

在本节中，我们介绍了用于感知的系统模型、距离模糊以及雷达系统中用于消除模糊的现有方法。¹

A. System model for sensing

本文的 RS 研究考虑了双基感知，例如基站 (BS) 到 BS 的双基感知、BS 到用户设备 (UE) 或 UE 到 BS 的双基感知等。为了一般性，以 BS 到 UE 的双基感知为例，其系统模型如图 1(a) 所示。需要注意的是，对于单基感知，由于感知发射机和接收机位于同一位置，随机的通信数据和感知 RS 都可以用于感知。

根据感知测量的要求，感知用例可分为多种类型，包括目标检测 (例如，目标存在性/目标数量等)、目标参数估计 (例如，距离/速度/角度估计)、识别和成像等。在本文中，目标检测和参数估计是研究的重点。关键性能指标 (KPI) 包括分辨率、精度和最大无模糊性能。此外，作为 RS 设计的通用 KPI，也应特别考虑 ISAC 系统中的 RS 开销，以减少对通信性能的影响。

正交频分复用 (OFDM) 波形在 ISAC 系统中被加以考虑，其估计性能由感知 RS 的资源和模式决定，如图 2 所示。得益于 OFDM 的优势，距离和速度可以分别在频域和时域中独立估计，这表明频域和时域中的 RS 模式可以分开设计。在本文中，我们专注于距离估计，其中速度或多普勒频移假定为零。

在这里插入图片描述

对于距离估计，占用带宽决定了分辨率和估计精度，这与系统配置有关。例如，NR 中支持最大 400 MHz 带宽，可实现 0.375 m 的分辨率。对于子载波间隔 (SCS) 为 $Δf\Delta f$ 的 OFDM 系统，梳齿尺寸为 $L$ 且消耗较低开销的稀疏 RS 将导致有效 SCS 为 $LΔfL\Delta f$ ，并将最大无模糊距离减小 $1L\frac{1}{L}$ 。通过以上分析，我们可以发现 RS 模式主要影响最大无模糊性能和 RS 开销，而分辨率和精度性能则更多地与系统配置和可用资源相关。因此，最大无模糊距离和 RS 开销是本文中感知 RS 模式设计的 KPI。

¹在本文中，感知 RS 和通信数据在正交的资源单元 (REs) 上进行复用，假设感知和通信之间没有干扰。因此，系统模型和 RS 设计仅关注感知部分。

B. Distance ambiguity and elimination method in radar

在雷达系统中，模糊也是一个重要的问题。为了便于理解，最大无模糊距离的定义如图 1(b) 所示。可以发现，脉冲重复间隔 (pulse
repetition interval，PRI) 将决定无模糊的最大延迟 (即距离)。当反射信号的延迟大于 PRI 时，感知接收机无法区分该信号是由第一个信号脉冲还是第二个信号脉冲反射的，从而导致模糊。

消除雷达系统中距离模糊的一种常用方法是多重脉冲重复频率 (multiple pulse repetition frequency，PRF) 传输。其基本原理是发射具有不同 PRF 的多个雷达脉冲。例如，对于 PRI 分别为 $T_1$ 和 $T_2$ 的两个脉冲，如图 3 所示，最大无模糊距离可由 $T_1$ 和 $T_2$ 的最小公倍数 (lcm) 决定，即 $PRF1=1T1\text{PRF}_1 = \frac{1}{T_1}$ 和 $PRF2=1T2\text{PRF}_2 = \frac{1}{T_2}$ 的最大公约数 (gcd)。当多个脉冲的 PRF，即 $PRF1\text{PRF}_1$ 和 $PRF2\text{PRF}_2$ 互质时，它们的最大公约数为 $1$ ，此时可以获得最大的无模糊距离。

III. ANALYSIS OF COMB RS AND NR PRS

为了更清晰地理解如何使用现有 RS 进行感知，本节分析了梳状 RS 和 NR PRS 的特性和感知性能。

A. Comb RS and sensing performance

在 OFDM 系统中，第 $m$ 个 OFDM 符号的连续时域信号可以表示为

$sm(t)=∑n=0Nm−1xm,nej2πfm,nt⋅rect(t−mTsTs)(1)s_m(t) = \sum_{n=0}^{N_m-1} x_{m,n} e^{j2\pi f_{m,n} t} \cdot \text{rect}\left(\frac{t-mT_s}{T_s}\right) \tag{1}$

其中 $x_{m,n}$ ( $\dots, N_m-1$ ) 表示长度为 $N_m$ 的 RS 序列， $f_{m,n}$ 表示第 $m$ 个 OFDM 符号上承载 RS 信号的第 $n$ 个子载波的频率， $Ts=1ΔfT_s = \frac{1}{\Delta f}$ 是一个 OFDM 符号的持续时间，且当 $\le x \le 1$ 时 $rect(x)\text{rect}(x)$ 为 1，否则为 0。

梳状 RS (Comb RS) 是通信系统中的一种常用 RS 模式，因此也是一种重要的候选 RS 模式，尤其适用于 ISAC (Integrated Sensing and Communication) 系统中的感知功能。对于第 $m$ 个 OFDM 符号上梳齿大小为 $L_m$ 且频率偏移为 $k_m$ 的梳状 RS，有 $fm,n=(nLm+km)Δff_{m,n} = (nL_m + k_m)\Delta f$ 。将其代入 (1)，可以推导出第 $m$ 个 OFDM 符号上的 $N$ 个采样点如下

$sm,i=sm(iTsN)=∑n=0Nm−1xm,nej2π(nLm+km)ΔfiTsN=(a)ej2πkmiN∑n=0Nm−1xm,nej2πnLmiN(2)s_{m,i} = s_m\left(\frac{iT_s}{N}\right) = \sum_{n=0}^{N_m-1} x_{m,n} e^{j2\pi(nL_m+k_m)\Delta f \frac{iT_s}{N}} \\ \stackrel{(a)}{=} e^{j2\pi k_m \frac{i}{N}} \sum_{n=0}^{N_m-1} x_{m,n} e^{j2\pi nL_m \frac{i}{N}} \tag{2}$

其中 $i=0,…,N−1i=0,\dots,N-1$ 并且 (a) 源于 $ΔfTs=1\Delta f T_s = 1$ 。通过将 $i=i'+lN_m$ （其中 $i′=0,…,Nm−1i'=0,\dots,N_m-1$ 且 $l=0,…,Lm−1l=0,\dots,L_m-1$ ）代入 (2)，我们可以推导出

$sm,i′+lNm=ej2πkmlLm⋅sm,i′(3)s_{m,i'+lN_m} = e^{j2\pi \frac{k_m l}{L_m}} \cdot s_{m,i'} \tag{3}$

这表明一个 OFDM 符号内的采样感知信号是第一个采样组（长度为 $N_m$ ）的循环重复，并带有相位旋转。采样组的数量与梳齿大小 $L_m$ 相等，每个采样组的相位旋转与频率偏移 $\le k_m \le L_m-1$ 相关，如图 4 所示，其中 $s0=[sm,0,…,sm,Lm−1]s_0 = [s_{m,0}, \dots, s_{m,L_m-1}]$ 表示第一组中的样本。由于这种重复性，感知信号的模糊函数会出现旁瓣（或者说等效的脉冲重复间隔 PRI 减小了），这将降低最大无模糊距离。

B. NR PRS and sensing performance

在这里插入图片描述

在 NR 中，PRS 是为 UE 定位而提出的。NR PRS 的设计基于三个步骤或原则。

首先，考虑使用梳状模式的 NR PRS 来支持如图 5(a) 所示的基于频分复用 (FDM) 的多端口。
其次，考虑到一个梳状 RS 的模糊问题，考虑了如图 5(b) 所示的具有不同频率偏移 $k_m$ 的多个交错梳状 RS。通过对多个带有交错梳状 RS 的符号进行联合估计，可以消除距离模糊 [7]。
第三，在要求低延迟的情况下，占用部分符号的 PRS 可用于在所有符号被接收之前进行位置估计。为了支持这类场景，即基于部分符号进行估计，交错梳状 RS 会被置换（permuted），并累积成更密集的符号，如图 5 $(c)$ 所示，这与 NR PRS 模式是一致的。交错梳状 RS 和 NR PRS 都可以提供等效于梳齿尺寸为 1 的 RS (或块状 RS)，但代价是因占用 $Ms≥LM_s \ge L$ 个符号而引起的高开销。

$Ms≥LM_s \ge L$ 是一个条件。它指出，为了让NR PRS能正常工作并消除模糊，所使用的OFDM符号数量（ $M_s$ ）必须大于或等于梳齿尺寸（L）。
为了支持这类场景，即基于部分符号进行估计，交错梳状 RS 会被置换，并累积成更密集的符号：这句话我感觉完全扯淡，不懂他在说什么

通过将梳齿尺寸 $L_m=L$ 和频率偏移 $k_m=m$ (对于 $M_s=L$ 个 OFDM 符号) 代入 (3)，我们可以得到 NR PRS 的表达式 $sm,i′+lNL=ej2πmlLsm,i′s_{m,i'+lN_L} = e^{j2\pi \frac{ml}{L}} s_{m,i'}$ ，其中 $NL=NLN_L = \frac{N}{L}$ ， $\le m,l \le L-1$ ，并且相位旋转因子由大小为 $L$ 的逆离散傅里叶变换 (IDFT) 矩阵确定。由于 IDFT 相位偏移的正交性，模糊函数中的旁瓣可以被消除，如图 6 所示。于是便可实现最大无模糊距离 $dmax=c2Δfd_{\text{max}} = \frac{c}{2\Delta f}$ 。

尽管 NR PRS 可以解决模糊问题，但由于最少需要 $L$ 个 OFDM 符号，其 RS 开销极高。因此，在不影响感知性能的前提下降低 RS 开销是研究的必要需求。

IV. PROPOSED SENSING RS

A. Proposed co-prime sensing RS pattern

雷达中的多重 PRF (multiple-PRF) 方法启发我们在 OFDM 系统的感知 RS 模式设计中引入互质特性。比较图 3 中的雷达脉冲和图 4 中 OFDM 的重复采样组，我们可以发现一个采样组可以被视为一个雷达脉冲。

为了验证基于 OFDM 信号模糊函数和雷达脉冲 PRI 的分析对于感知 RS 的最大无模糊性能是相同的，第 $m$ 个 OFDM 符号的模糊函数推导如下

$AFm(τ)=∫−∞∞sm(t)sm∗(t−τTs)dt=∑n1,n2=0Nm−1xm,n1xm,n2∗⋅∫−∞∞ej2πfn1te−j2πfn2(t−τTs)rect(t−mTsTs)rect(t−(m+τ)TsTs)dt=∑n1,n2=0Nm−1xm,n1xm,n2∗ej2π(n2Lm+km)τ∫(m+τ)Ts(m+1)Tsej2π(n1−n2)LmΔftdt=ej2πkmτ(1−τ)Ts∑n1,n2=0Nm−1xm,n1xm,n2∗ej2π(m+12τ)n1Lm⋅e−j2π(m+12τ)n2Lm⋅sinc((n1−n2)(1−τ)Lm),\begin{aligned} AF_m(\tau) &= \int_{-\infty}^{\infty} s_m(t)s_m^*(t - \tau T_s) dt = \sum_{n_1,n_2=0}^{N_m-1} x_{m,n_1} x_{m,n_2}^* \\ & \qquad \cdot \int_{-\infty}^{\infty} e^{j2\pi f_{n_1} t} e^{-j2\pi f_{n_2} (t-\tau T_s)} \text{rect}\left(\frac{t-mT_s}{T_s}\right) \text{rect}\left(\frac{t-(m+\tau)T_s}{T_s}\right) dt \\ &= \sum_{n_1,n_2=0}^{N_m-1} x_{m,n_1} x_{m,n_2}^* e^{j2\pi(n_2 L_m + k_m)\tau} \int_{(m+\tau)T_s}^{(m+1)T_s} e^{j2\pi(n_1-n_2)L_m \Delta f t} dt \\ &= e^{j2\pi k_m \tau} (1-\tau)T_s \sum_{n_1,n_2=0}^{N_m-1} x_{m,n_1} x_{m,n_2}^* e^{j2\pi\left(m+\frac{1}{2}\tau\right) n_1 L_m} \\ & \qquad \cdot e^{-j2\pi\left(m+\frac{1}{2}\tau\right) n_2 L_m} \cdot \text{sinc}\left((n_1-n_2)(1-\tau)L_m\right), \end{aligned}$

初始表达式与公因式提取

推导始于上一行末尾的表达式。首先，将与求和变量 $n_1, n_2$ 无关的项 $ej2πkmτe^{j2\pi k_m \tau}$ 提取到求和符号外部：

$e^{j2\pi k_m \tau} \sum_{n_1,n_2=0}^{N_m-1} x_{m,n_1} x_{m,n_2}^* e^{j2\pi n_2 L_m \tau} \int_{(m+\tau)T_s}^{(m+1)T_s} e^{j2\pi(n_1-n_2)L_m \Delta f t} dt$

求解核心积分项

令积分为 $I$ 。这是一个标准的指数积分。通过应用欧拉恒等式 $ejθ1−ejθ2=ejθ1+θ22⋅2jsin⁡(θ1−θ22)e^{j\theta_1} - e^{j\theta_2} = e^{j\frac{\theta_1+\theta_2}{2}} \cdot 2j \sin(\frac{\theta_1-\theta_2}{2})$ 并结合 $sinc\text{sinc}$ 函数的定义进行化简，可得其精确解为：

$T_s(1-\tau) \cdot \text{sinc}\left((n_1-n_2)(1-\tau)L_m\right) \cdot e^{j2\pi(n_1-n_2)L_m (m + \frac{1}{2} + \frac{\tau}{2})}$

代入积分结果并化简

将积分 $I$ 的解代回原式，并将与求和无关的系数 $Ts(1−τ)T_s(1-\tau)$ 提出：

$e^{j2\pi k_m \tau} T_s(1-\tau) \sum_{n_1,n_2} x_{m,n_1} x_{m,n_2}^* \text{sinc}(\dots) \cdot \left[ e^{j2\pi n_2 L_m \tau} \cdot e^{j2\pi(n_1-n_2)L_m (m+\frac{1}{2}+\frac{\tau}{2})} \right]$

合并指数项得到最终推导结果

合并求和符号 $∑\sum$ 内部的所有指数项，分别整理与 $n_1$ 和 $n_2$ 相关的部分，得到严格推导的最终表达式：

$e^{j2\pi k_m \tau} (1-\tau)T_s \sum_{n_1,n_2=0}^{N_m-1} x_{m,n_1} x_{m,n_2}^* \cdot e^{j2\pi n_1 L_m (m+\frac{1}{2}+\frac{\tau}{2})} \cdot e^{-j2\pi n_2 L_m (m+\frac{1}{2}-\frac{\tau}{2})} \cdot \text{sinc}(\dots)$

结论：与论文原文对比

将上述推导结果与论文给出的最终结果对比，可以发现两者在 sinc 部分和幅度项上完全一致，但在相位项上存在差异。这可能是原文在整理公式时出现的笔误，该差异不影响其关于模糊函数主旁瓣特性的核心结论。

推导相位: $ej2πn1Lm(m+12+τ2)⋅e−j2πn2Lm(m+12−τ2)e^{j2\pi n_1 L_m (m+\frac{1}{2}+\frac{\tau}{2})} \cdot e^{-j2\pi n_2 L_m (m+\frac{1}{2}-\frac{\tau}{2})}$
原文相位: $ej2πn1Lm(m+τ2)⋅e−j2πn2Lm(m+τ2)e^{j2\pi n_1 L_m (m+\frac{\tau}{2})} \cdot e^{-j2\pi n_2 L_m (m+\frac{\tau}{2})}$

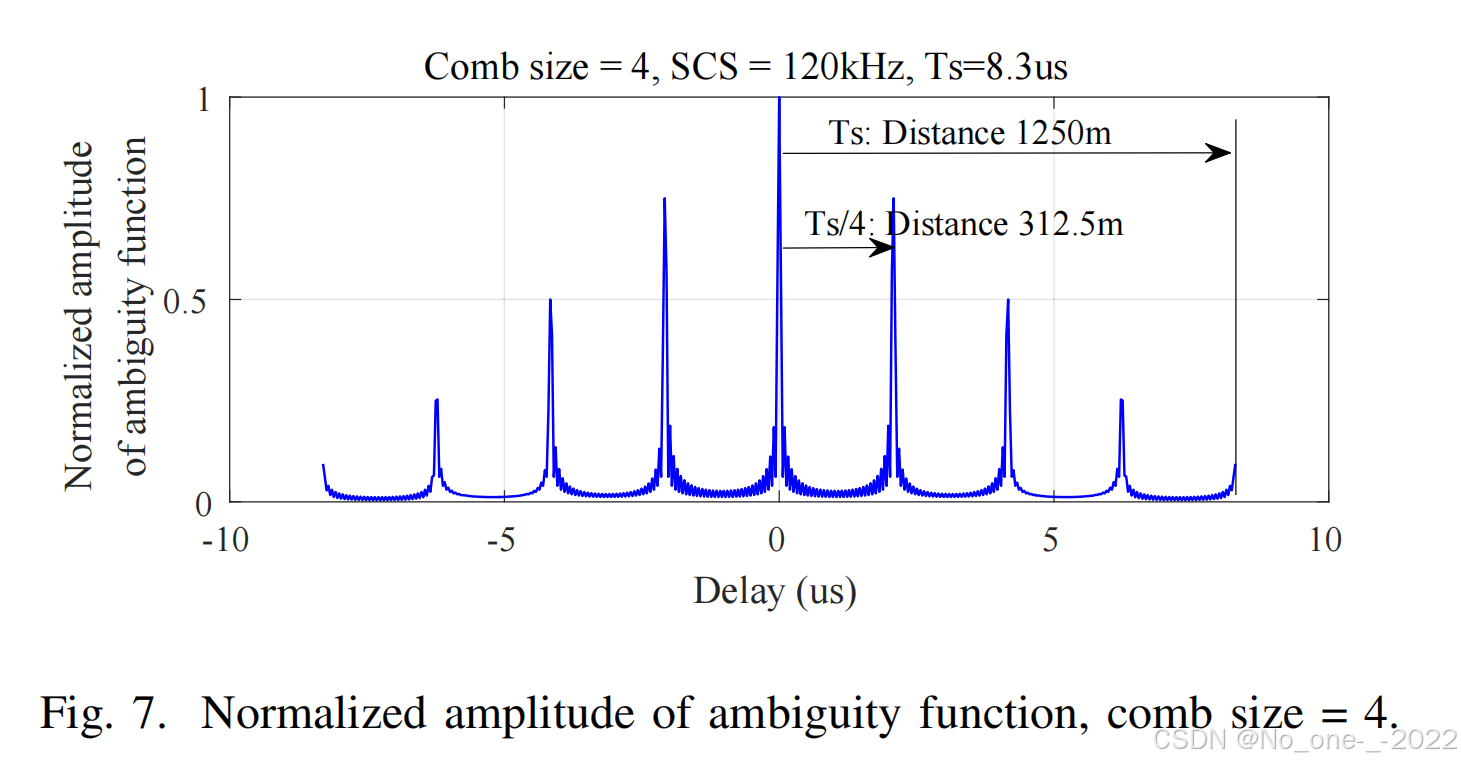
在这里插入图片描述

其中 $\le \tau \le 1$ 是由 $T_s$ 归一化的延迟，而 $sinc(x)=sin⁡(πx)πx\text{sinc}(x) = \frac{\sin(\pi x)}{\pi x}$ 是归一化的正弦函数。我们可以发现模糊函数的幅度仅由梳齿大小 $L_m$ 决定。 $^2$ 如图 7 所示，梳状模式会在模糊函数中位于 $TsLm\frac{T_s}{L_m}$ 处引起旁瓣。因此，最大无模糊距离由旁瓣决定，可以计算为 $dmax=Tsc2Lmd_{max} = \frac{T_s c}{2L_m}$ ，其中 $c$ 是光速，因子 2 来自往返延迟。

$^2$ RS 序列 $x_{m,n}$ 也会影响模糊函数，但这不是本文的研究重点。

具有梳齿大小 $L_m$ 的第 $m$ 个 OFDM 符号的 PRI 由一个采样组的持续时间决定。如第三节中所讨论的，一个 OFDM 符号中的重复次数等于 $L_m$ ，并且 PRI 计算为 $PRIm=TsLm\text{PRI}_m = \frac{T_s}{L_m}$ 。然后，最大无模糊距离由 PRI 决定，为 $dmax=PRImc2=Tsc2Lmd_{max} = \frac{\text{PRI}_m c}{2} = \frac{T_s c}{2 L_m}$ ，如图 1(b) 所示。我们可以发现，基于模糊函数和 PRI 分析可以获得相同的最大无模糊距离。第 $m$ 个 OFDM 符号的 PRF (脉冲重复频率) 可以推导为

$PRFm=1PRIm=LmTs=LmΔf(4)\text{PRF}_m = \frac{1}{\text{PRI}_m} = \frac{L_m}{T_s} = L_m \Delta f \tag{4}$

为了在 OFDM 系统中实现多重 PRF 方法，感知 RS 也应由 $M_s > 1$ 个具有不同梳齿大小 $L_m$ ( $m=0,⋯,Ms−1m=0,\cdots,M_s-1$ ) 的 OFDM 符号组成。等效 PRF 将由梳齿大小的最大公约数决定，如下所示

$LE=gcd(L0,⋯,LMs−1)(5)\text{PRF}_E = L_E \Delta f, \text{ 其中 } L_E = \text{gcd}(L_0, \cdots, L_{M_s-1}) \tag{5}$

最大无模糊距离为 $dmax=c2LEΔfd_{max} = \frac{c}{2 L_E \Delta f}$ 。

注记： 当梳齿大小互质时， $L_E = 1$ ，此时将实现最大的无模糊距离 $dmax=c2Δfd_{max} = \frac{c}{2\Delta f}$ ，这与 NR PRS (新空口定位参考信号) 的情况相同。实现梳齿大小互质所需的最小 OFDM 符号数为 2。

目标与基本关系

在多 PRF 系统中，首要目标是提升最大无模糊距离 $d_{max}$ 。根据距离公式 $dmax=PRI⋅c2d_{max} = \frac{\text{PRI} \cdot c}{2}$ ，这等效于最大化等效脉冲重复间隔 $PRIE\text{PRI}_E$ 。

从时间域确定等效周期 $PRIE\text{PRI}_E$

单个 OFDM 符号的脉冲重复间隔为 $PRIm=Ts/Lm\text{PRI}_m = T_s / L_m$ 。当组合多个具有不同 $PRIm\text{PRI}_m$ 的符号时，整个测量模式会形成一个新的、更长的重复周期。这个新的、能消除模糊的“超级周期” $PRIE\text{PRI}_E$ ，必须是所有单个周期的最小公倍数 (LCM)，因为只有这样才能保证整个模式第一次完整地重复。

$PRIE=LCM(PRI0,PRI1,…)=LCM(TsL0,TsL1,…)\text{PRI}_E = \text{LCM}(\text{PRI}_0, \text{PRI}_1, \dots) = \text{LCM}\left(\frac{T_s}{L_0}, \frac{T_s}{L_1}, \dots\right)$

转换为等效PRF并推导GCD关系

等效脉冲重复频率 $PRFE\text{PRF}_E$ 是等效重复间隔 $PRIE\text{PRI}_E$ 的倒数。利用这一关系以及数论倒数恒等式 $1LCM(1/a,1/b)=GCD(a,b)\frac{1}{\text{LCM}(1/a, 1/b)} = \text{GCD}(a,b)$ ，我们可以进行关键变换：

$PRFE=1PRIE=1LCM(TsL0,TsL1,…)=1Ts⋅LCM(1L0,1L1,…)\text{PRF}_E = \frac{1}{\text{PRI}_E} = \frac{1}{\text{LCM}\left(\frac{T_s}{L_0}, \frac{T_s}{L_1}, \dots\right)} = \frac{1}{T_s \cdot \text{LCM}\left(\frac{1}{L_0}, \frac{1}{L_1}, \dots\right)}$
应用倒数恒等式，上式变为：
$PRFE=1Ts⋅GCD(L0,L1,…)\text{PRF}_E = \frac{1}{T_s} \cdot \text{GCD}(L_0, L_1, \dots)$
由于 $Δf=1/Ts\Delta f = 1/T_s$ ，并定义 $LE=GCD(L0,L1,…)L_E = \text{GCD}(L_0, L_1, \dots)$ ，我们便得到了论文中的最终公式：
$PRFE=LEΔf\text{PRF}_E = L_E \Delta f$
这证明了：为了获得PRI的最小公倍数（最大化无模糊周期），我们必须对PRF对应的系数 $L_m$ 取最大公约数。

实例验证

假设有两个符号，其梳齿大小分别为 $L_0 = 6$ 和 $L_1 = 9$ 。

从时间域计算:
$PRIE=LCM(Ts6,Ts9)=Ts⋅LCM(16,19)=Ts⋅1GCD(6,9)=Ts3\text{PRI}_E = \text{LCM}\left(\frac{T_s}{6}, \frac{T_s}{9}\right) = T_s \cdot \text{LCM}\left(\frac{1}{6}, \frac{1}{9}\right) = T_s \cdot \frac{1}{\text{GCD}(6,9)} = \frac{T_s}{3}$
因此， $PRFE=1PRIE=3Ts=3Δf\text{PRF}_E = \frac{1}{\text{PRI}_E} = \frac{3}{T_s} = 3\Delta f$ 。

直接使用GCD公式:
$LE=GCD(6,9)=3L_E = \text{GCD}(6, 9) = 3$
因此， $PRFE=LEΔf=3Δf\text{PRF}_E = L_E \Delta f = 3\Delta f$ 。

两种方法结果一致。新的等效间隔 $PRIE=Ts/3\text{PRI}_E = T_s/3$ 比原来的 $T_s/6$ 和 $T_s/9$ 都长，成功增大了无模糊距离。

尽管所有满足互质条件的整数都可以被视为我们提出的感知 RS 模式中的梳齿大小，但下面将针对 2 个 OFDM 符号介绍两个特殊示例，它们具有易于定义的优点。

示例 1： 任何整数 $\ge 1$ 都与 1 互质。该感知 RS 模式由一个块状 RS (block RS) 和一个梳齿大小为 $L$ 的梳状 RS (comb RS) 组成，如图 8 所示。然而，块状 RS 会消耗很高的开销，并且不适用于占据整个带宽。因此，为了保持低开销，块状 RS 可以占据部分带宽，提供一个粗略的距离估计，但具有较大的最大无模糊距离。另一个梳状 RS 则可以跨越整个带宽，提供一个精确的距离估计，但最大无模糊距离较小。然后，通过基于所提出的感知 RS 模式的两步估计法，可以同时获得精确的估计和大的最大无模糊距离，如图 8 所示。

在这里插入图片描述

示例 2： 对于任何 $\ge 1$ ，整数 $L$ 和 $L + 1$ 都是互质的。该感知 RS 模式由两个梳齿大小分别为 $L$ 和 $L + 1$ 的梳状 RS 组成。例如，两个 OFDM 符号的梳齿大小可以是 {3, 4} 或 {6, 7} 等。考虑到对于梳齿大小为 { $L, L + 1$ } 的组合，开销是相似的，两个梳状 RS 都可以占据整个带宽以进行精确的距离估计。
其他示例： 对于任何奇数 $\ge 1$ ，奇数 $L$ 和 $L + 2$ 是互质的，或者任何奇数 $\ge 1$ 与 2 互质。

NR PRS 与所提出的感知 RS 之间存在两个区别。首先，对于所提出的感知 RS，OFDM 符号的数量独立于梳齿大小，仅要求大于 1，而在 NR PRS 中，它需要等于或大于梳齿大小 $L$ 。这表明所提出的 RS 具有低得多的 RS 开销。其次，在所提出的感知 RS 中，多个 OFDM 符号的梳齿大小应该是互质的，而在 NR PRS 中，所有符号都使用一个梳齿大小。尽管多个 OFDM 符号的梳齿大小不同，但在所提出的感知 RS 模式中，每个 OFDM 符号使用一个统一的梳齿大小，这表明其具有良好的后向兼容性。