AI时代大数据分布的深入洞察与应用

如何识别并利用大数据集的概率分布。揭示损失函数与概率分布之间深刻的内在联系，并提供一套在海量数据背景下的分布判断实践流程。

1 识别一个大数集服从什么分布有什么意义

在深度学习的浪潮下，一种观点认为，只要拥有足够大的模型和海量数据，模型就能“自动”学习一切，包括数据内在的复杂分布，从而使得传统的分布识别工作变得多余。这种看法忽略了问题的本质：理解数据分布的意义体现在三个层次。

首先，在工程实践层面，对分布的认知是构建高效、鲁棒模型的基石

例如，数据预处理中的标准化目的不止是统一量纲，更深层的认知是：大多数优化算法（如梯度下降）在“圆形”的损失等高面上效率最高，而标准化正是将不同尺度、不同分布的特征“塑造”成近似标准正态分布，从而优化了学习过程。

同样，对数变换的广泛应用，源于我们识别出许多现实世界数据（如收入、点击量）服从右偏的对数正态分布或幂律分布。这一操作将非线性的乘法关系转换为线性的加法关系，有效抑制了极端值对模型的过度影响。

此外，对分布的理解直接决定了我们如何界定“异常”，为无监督异常检测和构建模型的安全边界提供了理论依据，这在金融风控、自动驾驶等高风险领域至关重要。

其次，在模型设计层面，分布的理解是我们构建模型“世界观”的蓝图

无论是变分自编码器（VAE）还是扩散模型，它们的终极目标都是学习并复现训练数据的真实概率分布。例如，VAE的核心假设就是复杂的数据分布可以由一个简单的先验分布（通常是标准正态分布）通过神经网络映射生成。

扩散模型则巧妙地将数据分布逐步“退化”为一个已知的高斯噪声分布，再学习其逆过程。

如果我们对真实数据分布的几何特性（如多峰性、流形结构）有先验认知，便能设计出更合理的模型架构和采样策略。

最后，在认知科学的前沿，对分布的探索是AI从“相关性”迈向“因果推理”的阶梯。

当前的大模型是卓越的相关性学习者，但无法回答“如果……会怎样？”的因果问题。因果推断的数学框架，其核心就是将复杂的联合分布分解为一系列由因果机制决定的、更简单稳定的局部条件概率分布。识别并解构数据分布，是迈向因果理解的第一步。识别和重构数据的真实分布结构，是AI想从“统计模拟”跨越到“因果理解”的必要条件。

2 常见数据分布

离散型: 数据只能取有限个或可数个值

例子: 抛硬币的结果（正面/反面）、产品评论的星级、一天内网站的访问次数。

候选分布:

伯努利分布: 适用于只有两个可能结果的单次试验（如：用户是否点击广告）。

二项分布: n次独立伯努利试验中成功的次数。

泊松分布: 在固定时间/空间内，某事件发生的次数（如：每小时客服中心接到的电话数）。

多项分布: 类似于伯努利，但结果有k个（k>2）的单次试验（如：掷骰子的点数）。

连续型: 数据可以取某个区间内的任何值

例子: 人的身高、房屋的面积、传感器的温度读数。

候选分布:

均匀分布: 在一个区间内，所有值的可能性都相等。

正态分布: 自然界和工程中极其常见，呈钟形曲线。

指数分布: 描述独立事件发生的时间间隔（如：两次公交车到站的间隔时间）。

伽马分布 (Gamma) / 对数正态分布 (Log-Normal): 通常用于描述偏态数据，如收入水平、保险索赔金额。

3 损失函数的选择本质上是对数据分布的假设

在机器学习工作流中，每一个主流损失函数的选择，都等价于我们对数据生成过程做出了一个明确的概率分布假设。连接这两者之间的桥梁，正是最大似然估计。其核心思想是：调整模型参数，使得观测到的这组数据出现的概率（似然）最大化。而最小化损失函数，在数学上往往等价于最大化对数似然函数。理解了“损失函数即分布假设”这一核心思想，当模型效果不佳时，可以反思其损失函数所隐含的假设是否与真实数据特性相匹配。

最经典的例子是回归任务中的均方误差。当我们选择MSE作为损失函数时，我们隐含地假设了模型的误差项服从均值为0的正态分布（高斯分布）。这意味着，如果数据的残差确实近似正态分布，MSE便是最优选择。反之，如果数据中存在大量异常值，导致误差分布呈现“重尾”特性，MSE就会因为平方项的放大作用而惩罚过度，导致模型被异常值带偏。

当我们选择平均绝对误差时，我们实质上是在假设模型误差服从拉普拉斯分布。拉普拉斯分布形态上更高尖、尾部更厚，它认为出现极端值的概率比正态分布更高。由于其误差是线性增长的，MAE对异常值的敏感度远低于MSE，因此在数据噪声较大或存在异常值时，模型会更加鲁棒。

当我们为多类别分类任务选择交叉熵损失函数时，我们是在假设样本的标签y服从以模型输出概率为参数的多项分布。对于二分类问题，则是伯努利分布。最大化这种离散分布的对数似然函数，直接导出了交叉熵损失的形式。

4 给定一个大数据集 如何判断它服从什么分布

包含以下3个步骤。是以可视化分析为驱动，以参数估计和模型比较为决策依据的综合性方法。

第一步：基础探索，理解数据本质。 这是所有分析的起点。首先，必须明确变量是离散型（如用户评分、点击次数）还是连续型（如身高、温度）。这直接决定了我们的候选分布范围（如离散的泊松分布、二项分布；或连续的正态分布、指数分布）。随后，计算描述性统计量，包括均值、中位数、标准差、偏度和峰度。这些数值为我们提供了关于分布中心、离散度和形状的初步线索。例如，若均值与中位数高度接近且偏度接近0，则数据可能具有对称性，如正态分布。

第二步：可视化分析，直观洞察形态。 对于大数据集而言，可视化是最强大、最可靠的直觉来源。“一图胜千言”，通过图形我们可以捕捉到数字无法完全表达的细微差别。

• 直方图：这是观察数据整体形状的首选。我们可以清晰地看到分布是钟形的（可能为正态）、平坦的（可能为均匀）、还是带有长尾的（可能为对数正态或指数）。同时，也能发现分布是单峰还是多峰，后者可能暗示数据来自多个混合的子群体。

• Q-Q图：用于严谨地比较样本分位数与某个理论分布（通常是正态分布）的分位数。如果数据点紧密地落在对角线（y=x）上，则表明样本与该理论分布高度拟合。系统性的偏离，如S形曲线或两端翘起，则精确地揭示了样本在偏度或尾部厚度上与理论分布的差异。

第三步：模型比较，做出最终的选择。 没有完美的模型，我们的目标就是找到“最佳近似”。

1. 选择候选分布：基于前几步的分析，挑选几个最有可能的分布族（例如，正态分布、t分布、伽马分布）。
2. 参数估计：对每个候选分布，使用最大似然估计找到最能拟合当前数据的参数。例如，为正态分布找到最优的均值μ和标准差σ。
3. 模型评估：使用**赤池信息准则（AIC）或贝叶斯信息准则（BIC）**来比较这些已经“尽力”拟合数据的模型。AIC和BIC都基于最大化后的似然值，并对模型复杂度（参数数量）施加惩罚。
4. 决策：选择AIC或BIC值最低的那个分布模型。它是在拟合优度和模型简洁性之间达到最佳平衡的选择。

4 一个实际例子

通过一个实际的数据拟合案例，演示如何使用最大似然估计进行分布拟合，并用AIC/BIC来选择最优分布模型。我们以日访问网站的用户数量为例，这是一个常见的、非负整数型的业务数据。我们猜测它可能符合以下三种分布之一：

正态分布（Normal）
对数正态分布（Log-normal）
伽马分布（Gamma）

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats# 示例数据：网站30天的访问量
data = np.array([120, 135, 128, 141, 130, 150, 152, 147, 149, 151,160, 155, 158, 162, 159, 170, 172, 175, 169, 165,180, 182, 179, 178, 185, 190, 192, 188, 195, 200])# 拟合三种分布
# 正态分布
norm_params = stats.norm.fit(data)
loglik_norm = np.sum(stats.norm.logpdf(data, *norm_params))
aic_norm = -2 * loglik_norm + 2 * 2
bic_norm = -2 * loglik_norm + 2 * np.log(len(data))# 对数正态分布（限制 loc=0 以便可解释性更强）
lognorm_params = stats.lognorm.fit(data, floc=0)
loglik_lognorm = np.sum(stats.lognorm.logpdf(data, *lognorm_params))
aic_lognorm = -2 * loglik_lognorm + 2 * 3
bic_lognorm = -2 * loglik_lognorm + 3 * np.log(len(data))# 伽马分布（限制 loc=0）
gamma_params = stats.gamma.fit(data, floc=0)
loglik_gamma = np.sum(stats.gamma.logpdf(data, *gamma_params))
aic_gamma = -2 * loglik_gamma + 2 * 3
bic_gamma = -2 * loglik_gamma + 3 * np.log(len(data))# 汇总结果
results = pd.DataFrame({'Distribution': ['Normal', 'Log-normal', 'Gamma'],'Log-Likelihood': [loglik_norm, loglik_lognorm, loglik_gamma],'AIC': [aic_norm, aic_lognorm, aic_gamma],'BIC': [bic_norm, bic_lognorm, bic_gamma]
})# 可视化原始数据与分布拟合
x = np.linspace(min(data), max(data), 1000)
pdf_norm = stats.norm.pdf(x, *norm_params)
pdf_lognorm = stats.lognorm.pdf(x, *lognorm_params)
pdf_gamma = stats.gamma.pdf(x, *gamma_params)
# 修改图表配置，确保中文能正确显示
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体中文字体
matplotlib.rcParams['axes.unicode_minus'] = False   # 解决负号显示问题# 重新绘图
plt.hist(data, bins=10, density=True, alpha=0.4, label='直方图（原始数据）')
plt.plot(x, pdf_norm, label='正态分布拟合')
plt.plot(x, pdf_lognorm, label='对数正态分布拟合')
plt.plot(x, pdf_gamma, label='伽马分布拟合')
plt.xlabel("访问量")
plt.ylabel("概率密度")
plt.title("网站访问量分布拟合")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

📊 使用 scipy.stats 里的工具，可以对这三种分布做参数拟合，手动计算三种分布的 log-likelihood，然后计算 AIC 和 BIC，做可视化分析。

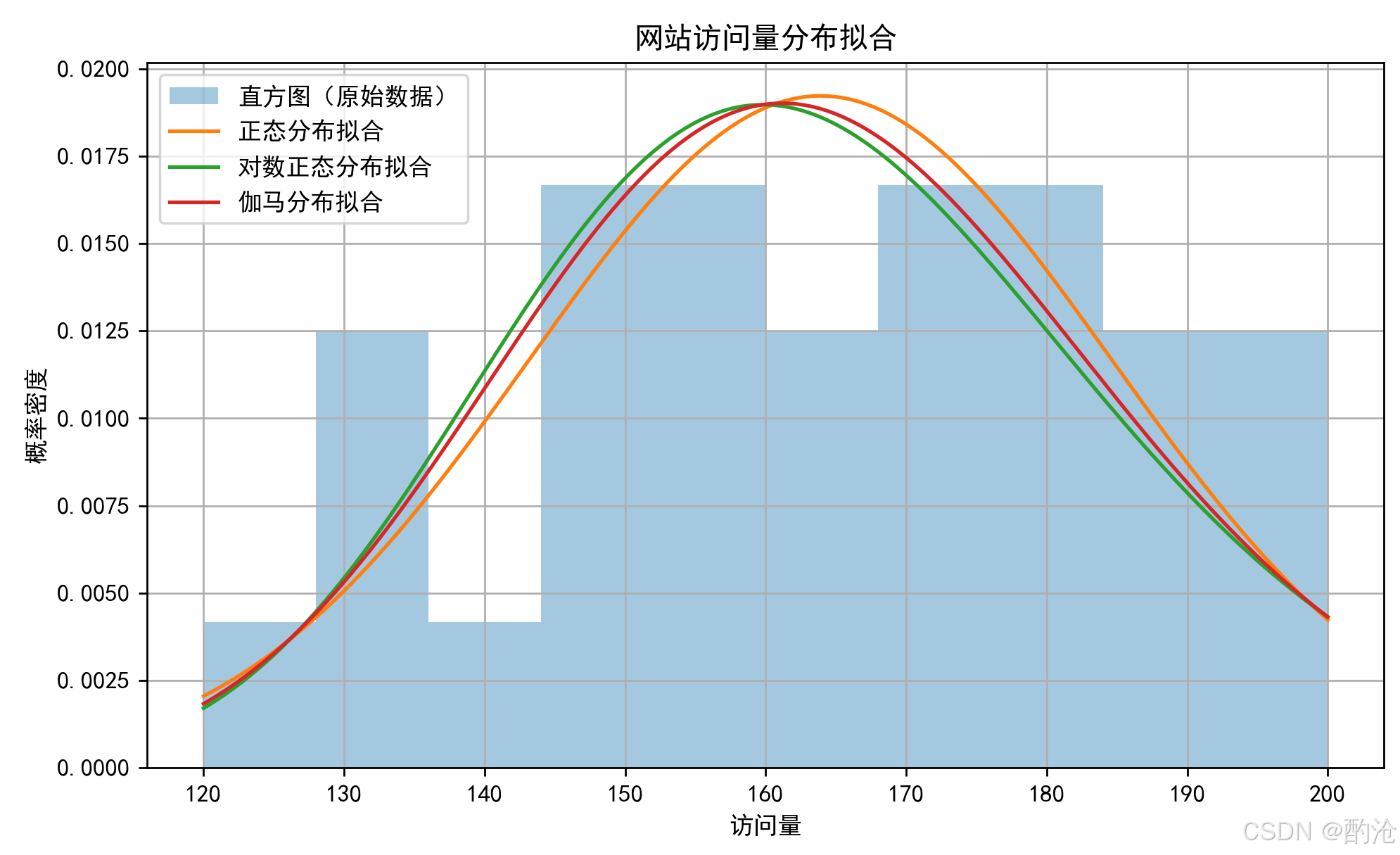
📊 我们观察到：正态分布（Normal）的 AIC最低，BIC也最低，所以，在这组访问量数据中，正态分布是最合适的拟合模型，它在拟合度和模型复杂度之间做到了最佳平衡。