当前位置：首页 > news >正文

Scikit-learn Python机器学习 - 聚类分析算法 - K-Means（K均值）

news 2025/9/28 7:47:01

锋哥原创的Scikit-learn Python机器学习视频教程：

https://www.bilibili.com/video/BV11reUzEEPH

课程介绍

本课程主要讲解基于Scikit-learn的Python机器学习知识，包括机器学习概述，特征工程(数据集，特征抽取，特征预处理，特征降维等)，分类算法(K-临近算法，朴素贝叶斯算法，决策树等)，回归与聚类算法(线性回归，欠拟合，逻辑回归与二分类，K-means算法)等。

Scikit-learn Python机器学习 - 聚类分析算法 - K-Means（K均值）

K-Means（K均值）聚类算法是一种常见的无监督学习算法，广泛用于数据挖掘和模式识别领域。其主要目标是将数据集分为多个簇（cluster），使得同一簇中的数据点相似度较高，而不同簇之间的数据点相似度较低。

K-Means 聚类的基本原理

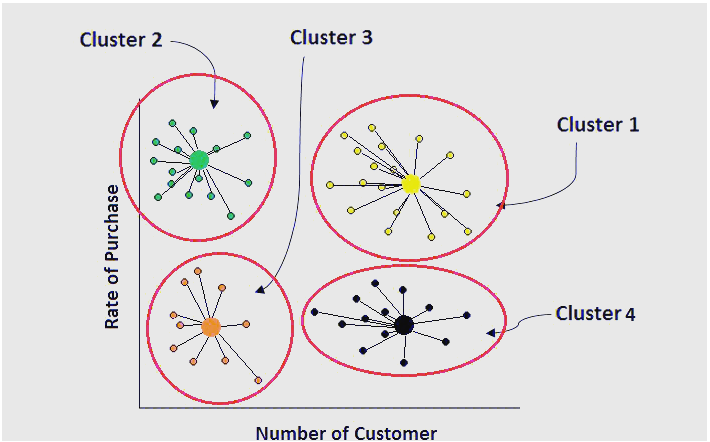
初始化： 随机选择K个数据点作为初始质心（centroid），其中K为预先设定的簇的数量。
分配步骤： 对于每个数据点，计算它与K个质心的距离，并将其分配到离它最近的质心所在的簇中。
更新步骤： 一旦所有数据点都被分配到簇中，重新计算每个簇的质心，即计算簇内所有点的均值，并将该均值作为新的质心。
重复： 重复执行分配和更新步骤，直到簇的质心不再发生显著变化或达到最大迭代次数为止。

K-Means（K均值）算法数学原理

1，K-Means 算法目标

2，K-Means 算法步骤

3，K-Means 算法的数学原理：优化目标

K-Means 算法的目标是通过迭代过程最小化目标函数（总误差平方和），这个目标函数即：

K-Means 聚类的优缺点

优点：

计算效率高： 对于大数据集，K-Means是非常高效的，时间复杂度是 O(n⋅k⋅t)，其中n是样本数，k是簇的个数，t是迭代次数。
简单易懂： K-Means算法的原理简单，易于实现。

缺点：

K值的选择： 需要事先指定簇的个数K，但K的选择并不容易，且过多或过少的簇数会导致聚类效果差。
容易受初始值影响： K-Means对初始质心非常敏感，容易陷入局部最优解。
不能处理非球形簇： K-Means假设每个簇是球形的，因此对于形状不规则的簇，K-Means可能效果不好。
对噪声敏感： 对异常值（outliers）比较敏感，可能影响聚类效果。

API介绍

在使用 Python 的 Scikit-Learn 库时，我们使用KMeans 类来实现K-Means聚类算法：

from sklearn.cluster import KMeansmodel = KMeans(n_clusters=8,init='k-means++',n_init=10,max_iter=300,random_state=42
)

核心参数：

n_clusters（最重要的参数）:
- 含义：要形成的簇数，也就是 K 值。
- 说明：这是你必须指定的参数，因为算法无法自动知道数据应该分成几类。K 值的选择对结果影响巨大，通常需要使用肘部法则或轮廓系数等方法来辅助确定最佳 K 值。
init（初始化方法）:
- 含义：初始化质心的策略。
- 选项：
  - ‘k-means++’（默认）：一种智能初始化方法，能有效加速收敛，并降低陷入局部最优解的风险。通常推荐使用这个。
  - ‘random’：完全随机选择 K 个初始质心。
  - ndarray：可以手动指定一个包含初始质心坐标的数组。
n_init:
- 含义：算法用不同的质心种子运行的次数。
- 说明：由于 K-Means 的结果受初始质心影响很大，可能会陷入局部最优。因此，算法会运行 n_init 次（每次使用不同的随机初始质心），并最终选择总簇内平方和（ inertia）最小的那次作为最终结果。
max_iter:
- 含义：单次运行中的最大迭代次数。
- 说明：如果算法在达到 max_iter 之前已经收敛（质心稳定），则会提前停止。300 通常已经足够。
random_state:
- 含义：随机数种子。
- 说明：指定一个整数可以使每次运行的结果保持一致，便于复现实验。如果不指定，每次运行结果可能略有不同。

具体示例

import numpy as np
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt# 生成一些样本数据
X = np.random.rand(100, 2)  # 100个2维数据点
# 创建KMeans模型，设定簇的个数K=3
kmeans = KMeans(n_clusters=3, random_state=0)# 训练KMeans模型
kmeans.fit(X)# 获取每个数据点的簇标签
labels = kmeans.labels_# 获取簇的质心
centroids = kmeans.cluster_centers_
print(centroids)
# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')  # 根据簇标签着色
plt.scatter(centroids[:, 0], centroids[:, 1], marker='*', color='red')  # 绘制质心
plt.show()

运行结果：

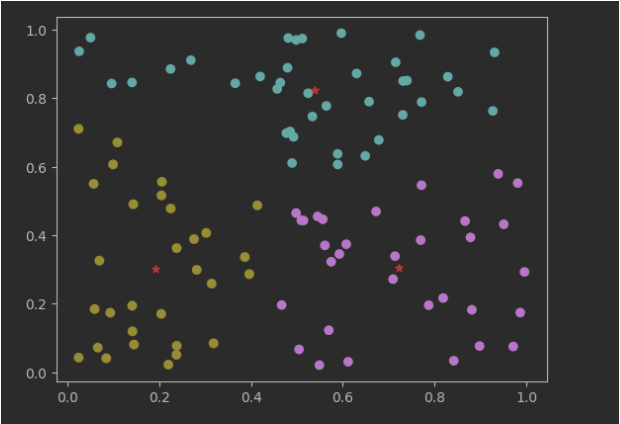
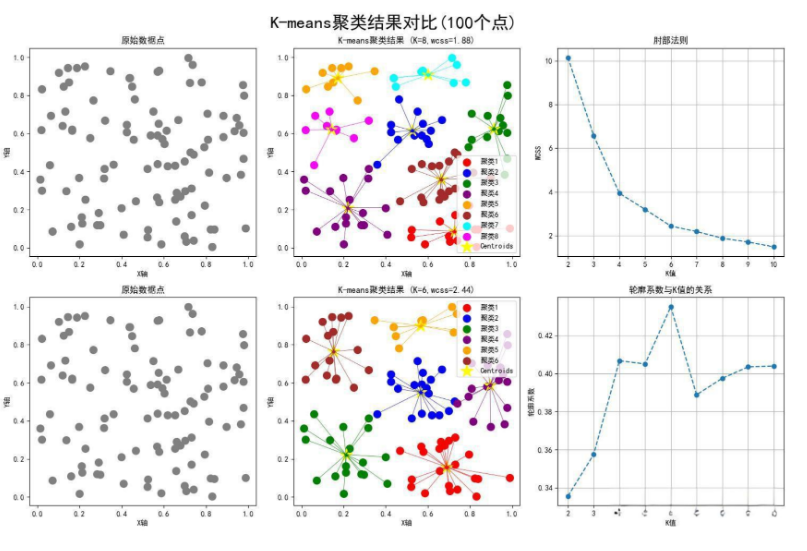
如何选择合适的K值

选择K值是K-Means聚类中的一个关键问题，常用的两种方法是：1，肘部法则（Elbow Method）2，轮廓系数（Silhouette Score）

1，肘部法则（Elbow Method）

通过计算不同K值下的聚类误差平方和（SSE，Sum of Squared Errors），绘制出K值与SSE的关系图。当K值增加时，SSE会逐渐减小，但当K达到某个值时，SSE的下降速率会显著变缓，这个拐点就是理想的K值（"肘部"）。

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
sse = []
for k in range(1, 11):kmeans = KMeans(n_clusters=k, random_state=0)kmeans.fit(X)sse.append(kmeans.inertia_)plt.plot(range(1, 11), sse)
plt.xlabel('K值')
plt.ylabel('SSE值')
plt.title('肘部法则选K值')
plt.show()

运行结果：

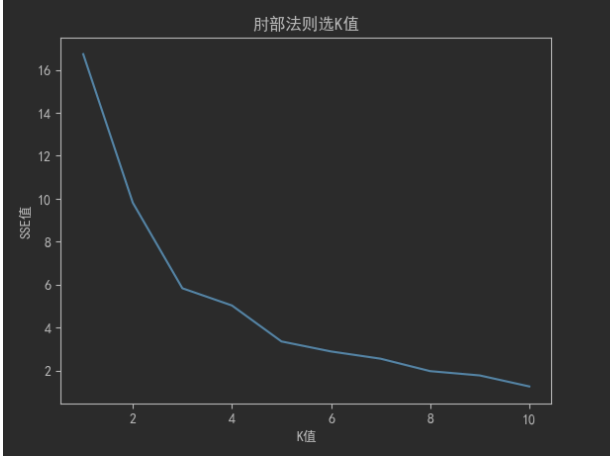
kmeans.inertia_ 是 KMeans 聚类算法中的一个属性，它表示聚类结果的 惯性（inertia）。简单来说，惯性是所有样本点与其所属簇的质心之间的平方距离的总和。惯性值越小，说明聚类结果越紧凑。

具体来说，kmeans.inertia_ 计算的是以下公式的总和：

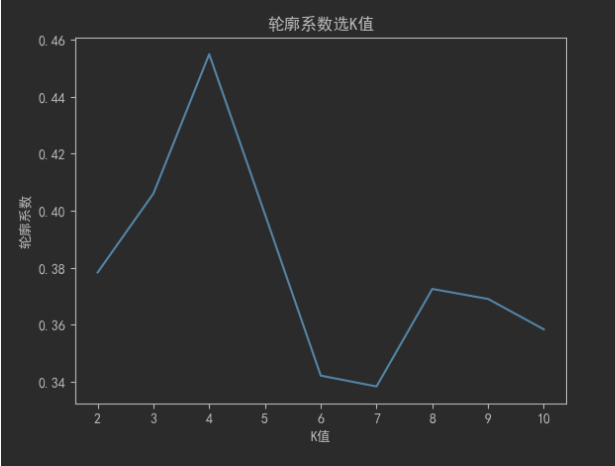
2，轮廓系数（Silhouette Score）

通过计算轮廓系数来评估不同K值的聚类效果，轮廓系数介于-1和1之间，值越大表示聚类效果越好。

from sklearn.metrics import silhouette_score# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
silhouette_scores = []
for k in range(2, 11):  # 至少需要2个簇kmeans = KMeans(n_clusters=k, random_state=0)kmeans.fit(X)score = silhouette_score(X, kmeans.labels_)silhouette_scores.append(score)plt.plot(range(2, 11), silhouette_scores)
plt.xlabel('K值')
plt.ylabel('轮廓系数')
plt.title('轮廓系数选K值')
plt.show()

项目运行截图：