当前位置：首页 > news >正文

LeetCode 0812.最大三角形面积：三角形面积公式考察

news 2025/9/28 5:17:35

【LetMeFly】812.最大三角形面积：三角形面积公式考察

力扣题目链接：https://leetcode.cn/problems/largest-triangle-area/

给你一个由 X-Y 平面上的点组成的数组 points ，其中 points[i] = [x_i, y_i] 。从其中取任意三个不同的点组成三角形，返回能组成的最大三角形的面积。与真实值误差在 10^-5 内的答案将会视为正确答案。

示例 1：

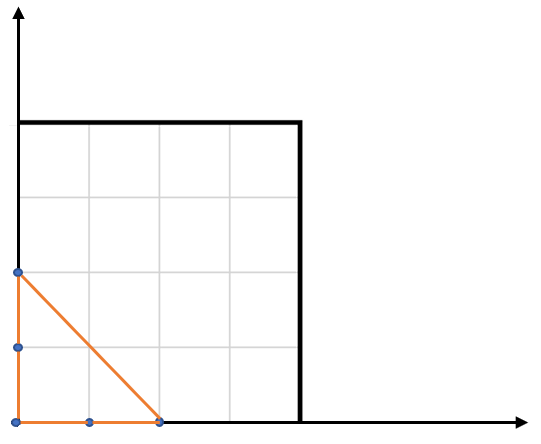
输入：points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
输出：2.00000
解释：输入中的 5 个点如上图所示，红色的三角形面积最大。

示例 2：

输入：points = [[1,0],[0,0],[0,1]]
输出：0.50000

提示：

3 <= points.length <= 50
-50 <= x_i, y_i <= 50
给出的所有点 互不相同

解题方法：暴力

三角形面积公式怎么算，有这些方法：

假设二维平面三角形三个顶点的坐标 $A(x_1, y_1), B(x_2, y_2), C(x_3, y_3)$ ，

行列式公式（Shoelace公式）： $\frac{1}{2} | x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) |$
向量叉积公式：设 $AB⃗=(x2−x1,y2−y1),AC⃗=(x3−x1,y3−y1)\vec{AB} = (x_2-x_1, y_2-y_1), \vec{AC} = (x_3-x_1, y_3-y_1)$ ，则
$\frac{1}{2} | \vec{AB} \times \vec{AC} | = \frac{1}{2} | (x_2-x_1)(y_3-y_1) - (x_3-x_1)(y_2-y_1) |$
海伦公式（已知三边长 $a, b, c$ ）： $\sqrt{(x_2-x_3)^2 + (y_2-y_3)^2},\ b = \sqrt{(x_1-x_3)^2 + (y_1-y_3)^2},\ c = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}$
$\frac{a+b+c}{2},\ S = \sqrt{s(s-a)(s-b)(s-c)}$

时间复杂度 $O(len(points)^3)$
空间复杂度 $O (1)$

AC代码

C++

/** @Author: LetMeFly* @Date: 2025-09-27 12:53:08* @LastEditors: LetMeFly.xyz* @LastEditTime: 2025-09-27 15:10:05*/
class Solution {
private:inline int calc(vector<vector<int>>& points, int i, int j, int k) {int x1 = points[i][0], y1 = points[i][1];int x2 = points[j][0], y2 = points[j][1];int x3 = points[k][0], y3 = points[k][1];return abs((x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1));}
public:double largestTriangleArea(vector<vector<int>>& points) {int ans = 0;for (int i = 0; i < points.size(); i++) {for (int j = i + 1; j < points.size(); j++) {for (int k = j + 1; k < points.size(); k++) {ans = max(ans, calc(points, i, j, k));}}}return double(ans) / 2;}
};

Python

'''
Author: LetMeFly
Date: 2025-09-27 12:53:08
LastEditors: LetMeFly.xyz
LastEditTime: 2025-09-27 15:15:55
'''
from typing import List
from itertools import combinationsclass Solution:def largestTriangleArea(self, points: List[List[int]]) -> float:ans = 0for p1, p2, p3 in combinations(points, 3):x1, y1 = p2[0] - p1[0], p2[1] - p1[1]x2, y2 = p3[0] - p1[0], p3[1] - p1[1]ans = max(ans, abs(x1 * y2 - y1 * x2))  # 记得absreturn ans / 2

Python一行版

'''
Author: LetMeFly
Date: 2025-09-27 12:53:08
LastEditors: LetMeFly.xyz
LastEditTime: 2025-09-27 15:17:57
'''
from typing import List
from itertools import combinationsclass Solution:def largestTriangleArea(self, points: List[List[int]]) -> float:return max(abs((p2[0] - p1[0]) * (p3[1] - p1[1]) - (p2[1] - p1[1]) * (p3[0] - p1[0])) for p1, p2, p3 in combinations(points, 3)) / 2