CVPR2024 | ANDA | 通过集成渐近正态分布学习实现强可迁移对抗攻击
Strong Transferable Adversarial Attacks via Ensembled Asymptotically Normal Distribution Learning
- 摘要-Abstract
- 引言-Introduction
- 相关工作和预备知识-Related Work and Preliminaries
- 提出的方法-Proposed Methodg
- 随机BIM的渐近正态性-Asymptotic Normality of Stochastic BIM
- 渐近正态分布攻击-Asymptotically Normal Distribution Attack
- Multiple Implementations of ANDA-MultiANDA
- 实验-Experiments
- 结论与展望-Conclusion and Perspectives
论文链接
本文 “Strong Transferable Adversarial Attacks via Ensembled Asymptotically Normal Distribution Learning” 提出了一种名为 Multiple Asymptotically Normal Distribution Attacks(MultiANDA)的方法,旨在通过学习对抗扰动的分布来生成具有强转移性的对抗样本,以评估和增强深度神经网络的鲁棒性。
摘要-Abstract
Strong adversarial examples are crucial for evaluating and enhancing the robustness of deep neural networks. However, the performance of popular attacks is usually sensitive, for instance, to minor image transformations, stemming from limited information — typically only one input example, a handful of white-box source models, and undefined defense strategies. Hence, the crafted adversarial examples are prone to overfit the source model, which hampers their transferability to unknown architectures. In this paper, we propose an approach named Multiple Asymptotically Normal Distribution Attacks (MultiANDA) which explicitly characterize adversarial perturbations from a learned distribution. Specifically, we approximate the posterior distribution over the perturbations by taking advantage of the asymptotic normality property of stochastic gradient ascent (SGA), then employ the deep ensemble strategy as an effective proxy for Bayesian marginalization in this process, aiming to estimate a mixture of Gaussians that facilitates a more thorough exploration of the potential optimization space. The approximated posterior essentially describes the stationary distribution of SGA iterations, which captures the geometric information around the local optimum. Thus, MultiANDA allows drawing an unlimited number of adversarial perturbations for each input and reliably maintains the transferability. Our proposed method outperforms ten state-of-the-art black-box attacks on deep learning models with or without defenses through extensive experiments on seven normally trained and seven defense models.
强对抗样本对于评估和增强深度神经网络的鲁棒性至关重要。然而,常见攻击方法的性能通常较为敏感,例如,对微小的图像变换就会有明显反应,这源于其信息有限——通常只有一个输入示例、少数几个白盒源模型,以及不明确的防御策略。因此,精心构造的对抗样本容易过度拟合源模型,这就阻碍了它们对未知架构的迁移能力。在本文中,我们提出了一种名为多重渐近正态分布攻击(MultiANDA)的方法,该方法通过学习到的分布来明确表征对抗扰动。具体而言,我们利用随机梯度上升(SGA)的渐近正态性来近似扰动的后验分布,然后在这个过程中采用深度集成策略作为贝叶斯边缘化的有效替代方法,旨在估计一个高斯混合模型,以便更全面地探索潜在的优化空间。近似后的后验本质上描述了SGA迭代的平稳分布,它捕捉了局部最优解周围的几何信息。因此,MultiANDA允许为每个输入生成无限数量的对抗扰动,并且能够可靠地保持其迁移性。通过在七个正常训练模型和七个防御模型上进行的大量实验,我们提出的方法在攻击有防御或无防御的深度学习模型时,性能优于十种最先进的黑盒攻击方法。
引言-Introduction
该部分主要阐述研究背景、问题以及提出的方法和贡献。
- 研究背景:深度神经网络(DNNs)在诸多领域表现出色,但易受对抗攻击,研究如何创建强大的对抗样本有助于评估和增强DNN的鲁棒性。
- 现有问题:当前基于黑盒和迁移的对抗攻击算法生成的对抗样本,易过度拟合替代模型,难以攻击其他模型,且对微小变换敏感。虽有数据增强和改进的优化方法,但在未知DNN架构,特别是有防御策略的模型上,泛化能力仍有限。
- 提出方法:提出Multiple Asymptotically Normal Distribution Attacks(MultiANDA),利用随机梯度上升(SGA)的渐近正态性学习对抗扰动的真实最优后验分布,并通过深度集成策略设计高斯混合模型,以提高攻击的泛化性能。
- 主要贡献:提出MultiANDA实现基于迁移的对抗攻击,通过学习扰动分布提升对抗样本的泛化性;设计随机对抗攻击过程,利用SGA的渐近正态性和深度集成策略准确高效地估计扰动的后验分布;从学习的扰动分布中可生成无限数量的对抗样本,实验证明其在防御模型上也有较高攻击成功率;大量实验表明,MultiANDA优于十种最先进的黑盒攻击方法,在攻击先进防御模型时更具优势。

图1. 由ANDA/MultiANDA生成的对抗样本的扰动可视化结果,这些对抗样本成功欺骗了所有选定的正常训练模型(第一行)和防御模型(第二行)。
相关工作和预备知识-Related Work and Preliminaries
该部分聚焦黑盒和基于迁移的威胁模型,介绍相关研究及预备知识,为后续提出的方法做铺垫,具体内容如下:
- 黑盒对抗攻击:黑盒对抗攻击算法旨在通过最大化损失函数(如分类任务中的交叉熵损失),在 l ∞ l_{\infty} l∞ 范数约束下搜索对抗样本。早期的 FGSM 和 BIM 方法在白盒场景有效,但易于过拟合,难以迁移到未知架构。为提升对抗样本的转移性,现有方法可分为三类:第一类改进迭代优化过程,如考虑动量、Nesterov加速梯度和方差减少等;第二类攻击中间层,破坏关键的目标感知特征;第三类采用常用的泛化技术引入多样性,包括数据增强和其他集成增强策略 。此外,一些方法尝试确定明确的对抗分布,但存在局限性,如 PGD 样本分布密集,Nattack 基于查询且可扩展性弱,ADT 以自然输入为中心生成对抗样本,与本文方法应用场景不同。
- SGD的渐近正态性:Maddox等人指出SGD的轨迹可视为待优化随机变量的贝叶斯后验分布,基于此提出SWAG方法用于模型校准或不确定性量化。Mandt等人进一步分析了具有恒定学习率的SGD迭代的平稳分布,即SGD的渐近正态性。受深度集成启发,Wilson和Izmailov通过实证研究表明,使用多个随机初始化模型的SWAG可显著提升模型性能,这得益于混合高斯分布的多模态效应。本文借鉴这些理论对扰动的后验分布进行建模,以寻找强大的对抗样本。
提出的方法-Proposed Methodg
随机BIM的渐近正态性-Asymptotic Normality of Stochastic BIM
该部分主要围绕随机 BIM 的渐近正态性展开研究,通过理论依据、实验验证、优化目标设定三个方面,为后续 ANDA 和 MultiANDA 攻击方法的提出做了充分铺垫,具体内容如下:
- 理论依据:在特定条件下,随机梯度下降(SGD)会渐近收敛到以局部最优为中心的高斯分布。Mandt等人进一步证明,在一定假设下,学习率恒定且足够小的SGD在最终搜索阶段会收敛到平稳分布,该阶段的迭代可近似优化变量的后验分布,而训练批次随机性引入的梯度噪声对形成该分布起到关键作用。
- 实验验证:标准 BIM 优化过程是确定性梯度上升,与标准 SGA 不同。为模拟高斯极限分布,在 BIM 的每次迭代步骤中集成随机数据增强技术 AUG,引入随机梯度噪声,公式为
x
a
d
v
(
t
+
1
)
=
Φ
(
x
a
d
v
(
t
)
+
α
⋅
s
i
g
n
(
∇
x
L
(
A
U
G
(
x
a
d
v
(
t
)
)
,
y
)
⏟
δ
(
t
)
)
)
x_{a d v}^{(t+1)}=\Phi\left(x_{a d v}^{(t)}+\alpha \cdot sign(\underbrace{\nabla_{x} \mathcal{L}\left(AUG\left(x_{a d v}^{(t)}\right), y\right)}_{\delta^{(t)}})\right)
xadv(t+1)=Φ
xadv(t)+α⋅sign(δ(t)
∇xL(AUG(xadv(t)),y))
。采用小常数学习率策略(
α
=
ϵ
/
T
\alpha=\epsilon / T
α=ϵ/T ),推测改进后的随机BIM可作为近似贝叶斯推理算法。利用 t-SNE 技术可视化对抗扰动
δ
(
t
)
\delta^{(t)}
δ(t),对300次迭代的3张随机抽取的ImageNet图像的实验结果显示,其呈现高斯分布,验证了随机BIM算法渐近正态性的猜想。同时,观察到优化轨迹上梯度噪声明显增加,但不影响扰动收敛,且前10步收敛时协方差紧密,表明在该任务中,较小的
T
T
T 值(非针对性攻击中常为10)和重要的第一步(如FGSM的强攻击性能)使得早期迭代接近局部最优。

图2. 随机BIM(a)和本文提出的方法(b)生成的对抗扰动迭代轨迹的渐近正态分布示例。 - 优化目标设定:受上述实证研究结果启发,提出使用
n
n
n 个图像变换
A
U
G
i
(
⋅
)
AUG _{i}(\cdot)
AUGi(⋅) 形成小批量进行对抗攻击,以增强随机性,此时优化目标为
m
a
x
x
a
d
v
∑
i
=
1
n
L
(
A
U
G
i
(
x
a
d
v
)
,
y
)
s
.
t
.
∥
x
a
d
v
−
x
∥
∞
≤
ε
max _{x_{a d v}} \sum_{i=1}^{n} \mathcal{L}\left(AUG_{i}\left(x_{a d v}\right), y\right) \ \ \ s.t. \left\| x_{a d v}-x\right\| _{\infty} \leq \varepsilon
maxxadv∑i=1nL(AUGi(xadv),y) s.t.∥xadv−x∥∞≤ε.
进一步地,为更充分地探索高维潜在扰动空间,提高对抗样本对未知架构的可转移性,通过分布 ( Π δ ) (\Pi_{\delta}) (Πδ) 对对抗扰动进行显式建模,优化目标形式化为 m a x Π δ E δ ∼ Π δ ∑ i = 1 n L ( A U G i ( x + δ ) , y ) , s . t . ∥ δ ∥ ∞ ≤ ε max _{\Pi_{\delta}} \mathbb{E}_{\delta \sim \Pi_{\delta}} \sum_{i=1}^{n} \mathcal{L}\left(AUG_{i}(x+\delta), y\right) , s.t. \| \delta\| _{\infty} \leq \varepsilon maxΠδEδ∼Πδ∑i=1nL(AUGi(x+δ),y),s.t.∥δ∥∞≤ε .
此目标是上述目标的广义版本,有望为生成可转移的对抗样本表征足够的扰动信息。
渐近正态分布攻击-Asymptotically Normal Distribution Attack
该部分主要介绍了渐近正态分布攻击(ANDA)方法,这是一种利用随机梯度上升(SGA)的渐近正态性来近似对抗扰动后验分布的攻击方法,具体内容如下:
- 优化问题求解思路:为更好地解决前文中提出的优化问题,ANDA方法利用SGA的渐近正态性,类似迭代搜索对抗样本的方式进行求解。在求解过程中,省略投影函数 Φ ( ⋅ ) \Phi(\cdot) Φ(⋅) 和 s i g n ( ) sign() sign() 函数,因为它们不影响SGA的渐近正态性。
- 计算梯度与假设分布:计算每次变换后的对抗样本梯度,并将其记为增强感知扰动 δ i ( t ) \delta_{i}^{(t)} δi(t). 假设在每次迭代中增强的样本集合为 S S S,根据中心极限定理,随机梯度 δ ^ S \hat{\delta}_{S} δ^S 可看作样本 z ∈ S z \in S z∈S 的函数,即 δ ^ S ( z ) ≈ δ ( z ) + 1 n Δ δ ( z ) \hat{\delta}_{S}(z) \approx \delta(z)+\frac{1}{\sqrt{n}} \Delta \delta(z) δ^S(z)≈δ(z)+n1Δδ(z),其中梯度噪声 Δ δ ( z ) \Delta \delta(z) Δδ(z) 服从均值为0、协方差为 C ( z ) C(z) C(z) 的高斯分布,即 Δ δ ( z ) ∼ N ( 0 , C ( z ) ) \Delta \delta(z) \sim \mathcal{N}(0, C(z)) Δδ(z)∼N(0,C(z)),进而 δ ^ S ( z ) ∼ N ( δ ( z ) , 1 n C ( z ) ) \hat{\delta}_{S}(z) \sim \mathcal{N}\left(\delta(z), \frac{1}{n} C(z)\right) δ^S(z)∼N(δ(z),n1C(z))。由此可知,每次迭代中对抗扰动的先验分布自然是高斯分布。
- 近似后验分布:得益于SGD的渐近正态性,ANDA通过估计随机梯度上升在优化过程中平稳分布的均值和协方差矩阵,来近似对抗扰动的后验分布。采用迭代平均的方式,利用随机梯度序列近似对抗扰动的均值,公式为 δ ‾ ( t + 1 ) = ( t × n ) δ ‾ ( t ) + ∑ i = 1 n δ i ( t ) ( t + 1 ) × n \overline{\delta}^{(t+1)}=\frac{(t × n) \overline{\delta}^{(t)}+\sum_{i=1}^{n} \delta_{i}^{(t)}}{(t+1) × n} δ(t+1)=(t+1)×n(t×n)δ(t)+∑i=1nδi(t),最终 δ ˉ = δ ˉ ( T ) \bar{\delta}=\bar{\delta}^{(T)} δˉ=δˉ(T)。通过考虑迭代过程中的所有随机梯度,估计后验分布的协方差矩阵,公式为 σ = D D T n × T − 1 \sigma=\frac{D D^{T}}{n × T-1} σ=n×T−1DDT,其中 D D D 为偏差矩阵。
- 生成对抗样本:通过上述步骤,ANDA可以通过从估计的分布
N
(
δ
ˉ
,
σ
)
N(\bar{\delta}, \sigma)
N(δˉ,σ) 中采样扰动,为一个输入生成一个或无限个对抗样本。完整的ANDA方法流程如算法1所示。对多次数据增强的10次迭代扰动进行可视化,结果验证了ANDA方法的有效性。

Multiple Implementations of ANDA-MultiANDA
该部分主要介绍了ANDA的多重实现方法MultiANDA,通过改进ANDA,提升了对抗样本的多样性和攻击性能,具体内容如下:
- 提出原因:虽然ANDA能够近似以最优 x a d v ∗ x_{a d v}^{*} xadv∗ 为中心的真实后验分布,但仅探索单峰优化空间,限制了生成对抗样本的多样性。为解决这一问题,借助深度集成策略近似贝叶斯边缘化的优良泛化能力,提出MultiANDA方法。
- 实现方式:MultiANDA通过对ANDA进行多次(例如 K K K 次)重复,并在原始样本 x x x 上添加随机初始值来实现。在每次ANDA过程中,独立运行并得到相应的对抗扰动 δ ˉ k \bar{\delta}_{k} δˉk,之后对这些对抗扰动求平均,得到 δ ˉ m e a n = 1 K ∑ k = 0 K − 1 δ ˉ k \bar{\delta}_{mean }=\frac{1}{K} \sum_{k=0}^{K-1} \bar{\delta}_{k} δˉmean=K1∑k=0K−1δˉk,以此实现高斯混合分布的多峰边缘化。
- 对抗样本生成与效果:与ANDA类似,MultiANDA也能通过公式迭代获得对抗样本。并且,它可以从每个近似的高斯分布 N ( δ ˉ k , σ k ) N(\bar{\delta}_{k}, \sigma_{k}) N(δˉk,σk) 中采样,高效生成无限个对抗样本。在后续的实验中表明,MultiANDA在攻击能力上有显著提升,特别是在攻击防御模型时效果更为突出。
实验-Experiments
这部分主要通过一系列实验验证了MultiANDA和ANDA方法的性能,具体内容如下:
- 实验设置:使用ImageNet1k数据集,包含从ImageNet中随机抽取的1000张图像。评估模型分为两类,即7个正常训练模型(如Inception-v3、ResNet-50等)和7个先进防御模型(包括对抗训练模型、HGD、NRP等)。将三类基于迁移的攻击方法作为基线,包括聚焦数据增强的方法(如DIM、TIM等)、考虑特征重要性的FIA以及优化增强方法(如BIM及其变体等) 。
- 攻击正常训练模型:在选定的源模型和目标模型上生成并测试对抗样本,结果显示ANDA和MultiANDA在几乎所有情况下显著优于其他方法,无论是白盒还是黑盒设置。以ResNet-50为源模型生成的对抗样本进行进一步研究,发现ANDA和MultiANDA生成的对抗样本能成功欺骗更多目标模型,且可视化结果表明其扰动更集中在物体的语义区域,主导预测模型的决策。

表1. 所提攻击方法和基线攻击方法对五个正常训练模型的成功率(%)。“Sign”表示在白盒源模型上的结果。最佳/次佳结果以粗体/下划线显示。由于篇幅限制,此处仅展示对五个目标模型的性能。七个目标模型的完整结果见附录。
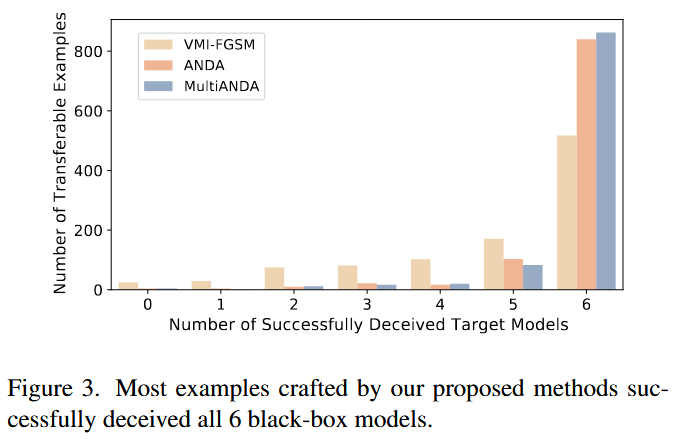
图3. 我们提出的方法生成的大多数样本成功欺骗了所有6个黑盒模型。 - 攻击防御模型:针对选定的先进防御模型评估方法性能,ANDA和MultiANDA在大多数情况下成功率显著提高,相比其他攻击方法有明显优势,尤其在以ResNet-50为源模型时达到总体最优成功率。同时发现,以VGG-19为源模型时,所有基线方法性能波动大且有效性普遍降低,凸显源模型选择对攻击转移性的关键作用。可视化结果再次表明,本文方法生成的扰动更集中在图像的关键信息区域。

表2. 所提方法和基线攻击方法对五个防御模型的攻击成功率(%)。最佳/次佳结果以粗体/下划线显示。由于篇幅限制,此处仅展示对五个目标模型的攻击性能。七个目标模型的完整结果见附录。 - 采样对抗样本的攻击性能:ANDA和MultiANDA可从学习的扰动分布中采样生成多个对抗样本。实验抽取20个对抗样本(
M
=
20
M = 20
M=20)并分析攻击成功率,结果显示采样得到的对抗样本与单个最优对抗样本相比,在攻击成功率上具有竞争力,即使在防御模型上也是如此,证实了扰动分布近似的有效性以及该方法在对抗训练或防御模型设计中的潜力。

图4. 由ANDA和MultiANDA生成的单个对抗样本 { δ ‾ } \{\overline \delta\} {δ}、多个对抗样本 { δ m } m = 1 20 \{\delta_{m}\}_{m = 1}^{20} {δm}m=120 (从学习到的扰动分布中为每个输入图像采样得到的20个对抗样本 )以及成功对抗样本 S u c . δ m m = 1 20 Suc. {\delta_{m}}_{m = 1}^{20} Suc.δmm=120(对应单个对抗样本攻击成功的输入图像所采样的20个对抗样本)的攻击成功率。
结论与展望-Conclusion and Perspectives
该部分对研究成果进行总结,并对未来研究方向提出展望,具体内容如下:
- 研究成果总结:提出多重渐近正态分布攻击(MultiANDA)方法来生成可转移的对抗样本,主要目标是通过高效近似对抗扰动的后验分布,实现对未知深度学习模型更好的泛化能力。利用优化轨迹上的梯度统计信息估计扰动的平稳分布,借助该学习到的分布,MultiANDA能显著提升对抗样本对黑盒目标模型的可转移性。大量实验表明,MultiANDA优于流行的和近期提出的黑盒及基于转移的攻击方法,这进一步凸显了当前防御技术的不足。同时,ANDA和MultiANDA的计算开销与类似基线方法相当,主要取决于增强时的批量样本数量,相比这些算法可能被滥用带来的潜在风险,其计算成本相对较低。
- 未来研究展望:倡导开发更符合人类视觉偏好的先进深度学习模型,以此避免现代模型中存在的基本缺陷,从根本上提升模型的安全性和鲁棒性,减少对抗攻击对模型的威胁。
