当前位置：首页 > news >正文

LeetCode刷题记录----62.不同路径（Medium）

news 2025/9/27 10:20:20

2025/9/26

题目（Medium）：

62.不同路径（Medium）

我的思路：

模式识别：要走到[m-1,n-1]就需要先走到[m-2,n-1]或者[m-1,n-2]的位置，而走到上述两个位置也需要同样往前推导，因此主问题和子问题有相同的结构和状态含义 --> 动态规划

因为是动态规划，所以我们要考虑各个状态以及状态的转移方程

显然需要对每个格子记录状态，所以我们用二维数组：

dp[i, j]：到达[i, j]位置的不同路径数

状态转移方程：dp[i, j] = dp[i-1, j] + dp[i, j-1] 【因为每次从左边或者上边的格子到达[i,j]一定只有一种方法】

初始状态：现在到达第一行或者第一列的格子都一定只有一条路径，所以都初始化为1

具体代码如下：

public class Solution {public int UniquePaths(int m, int n) {//第一行/第一列的格子显然都只有一种方式到达int[,] dp = new int[m, n];for(int j = 0; j < n; j++)dp[0, j] = 1;for(int i = 0; i < m; i++)dp[i, 0] = 1;//其他格子要到达，就一定要先到达她的左边，或者上边的格子。for(int i = 1; i < m; i++){for(int j = 1; j < n; j++){dp[i, j] = dp[i-1, j] + dp[i, j-1];}}return dp[m-1, n-1];}
}

时间复杂度：O（MN）

空间复杂度：O（MN）

优化思路：

１.压缩为一维动态规划

在上面的转移方程：dp[i, j] = dp[i-1, j] + dp[i, j-1] 中，我们可以看出来当前第 i 行，第j列的dp值只和它这一行的j-1列，以及上一行的j列元素有关。

因此我们可以考虑把他压缩为一维的，这样每次在计算新dp[j]的时候，都是计算最新一行的dp[j]值，同时对于还没计算的位置相当于保留了上一行的dp[j]的值。

新转移方程：dp[j] = dp[j] + d[j-1]

初始化：全部为1，因为第一行全部为1

翻译：当前行的dp[j] = 上一行的dp[j] + 当前行的dp[j-1]

具体代码如下：

public class Solution {public int UniquePaths(int m, int n) {//第一行/第一列的格子显然都只有一种方式到达int[] dp = new int[n];Array.Fill(dp, 1);//其他格子要到达，就一定要先到达她的左边，或者上边的格子。for(int i = 1; i < m; i++){for(int j = 1; j < n; j++){//dp[i, j] = dp[i-1, j] + dp[i, j-1];dp[j] += dp[j-1];       //可以压缩为一维的，因为可以看到每一行的状态只与这一行以及她的上一行有关}}return dp[n-1];}
}

时间复杂度：O（MN）

空间复杂度：O（N）

２.组合数

我们还可以通过数学原理，要到达m行，n列的位置，一共需要移动的次数为m+n-2次。其中需要向下移动的次数是m-1次，而题目要求的相当于就是在这m+n -2次中，选取m-1种不同的下移方案。

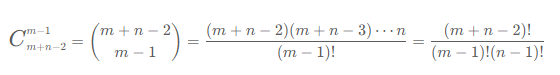
因此可以用该组合数公式来进行计算（公式图片来自于LeetCode官方题解）

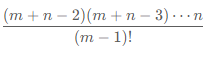
其中我们通过这里来下手，进行累乘计算（下面展示部分累乘过程）

n/1 ，(n /1) * (n+1/2)，（n/1) * (n+1/2) * (n+2/3) ...以此类推到最终答案值

因此我们可以用变量 x表示范围n ~ n + m -2 的分子，用变量y 表示范围1 ~ m-1的分母

具体代码如下：

public class Solution {public int UniquePaths(int m, int n) {//还可以计算组合数//一共要移动m+n-2次，其中存在m-1种往下移动的次数long ans = 1;long x, y; for(x = n, y = 1; y < m; x++, y++){ans = ans * x/ y;       //存在一个推导公式}return (int)ans;}
}

时间复杂度：O（M）

空间复杂度：O（1）