基于三角测量拓扑聚合优化的LSTM深度学习网络模型(TTAO-LSTM)的一维时间序列预测算法matlab仿真
目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.部分程序
4.算法理论概述
4.1 TTAO优化算法理论
4.2 TTAO优化LSTM网络模型
5.完整程序
1.程序功能描述
三角测量拓扑聚合优化的LSTM(TTAO-LSTM)模型,通过引入“三角测量拓扑聚合” 机制,将时间序列的局部特征与全局依赖进行结构化融合,同时优化LSTM的网络层数量,实现对复杂一维时间序列的高精度预测。
2.测试软件版本以及运行结果展示
MATLAB2022A/MATLAB2024B版本运行
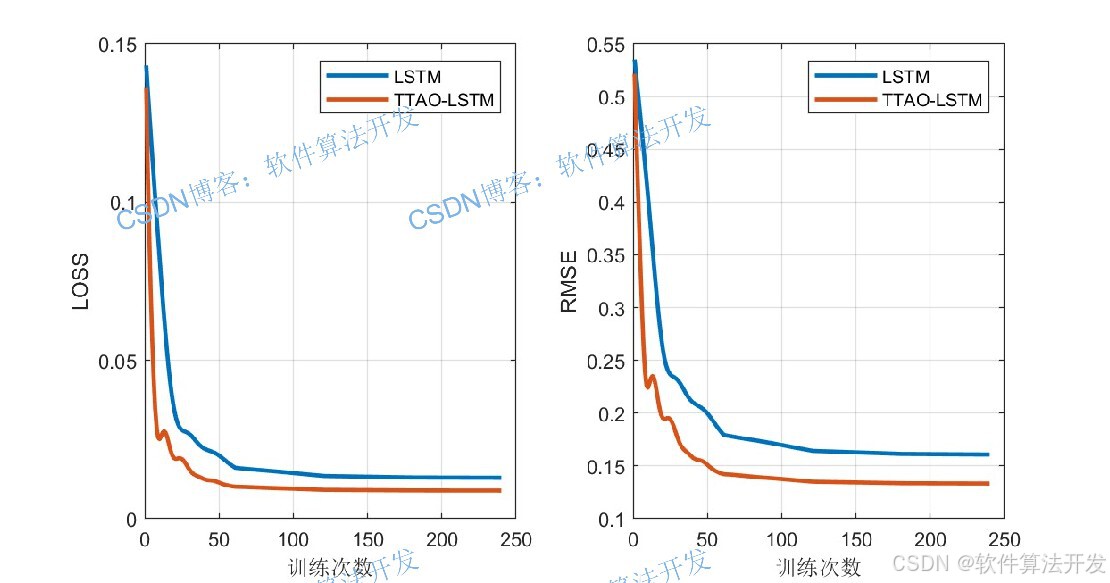
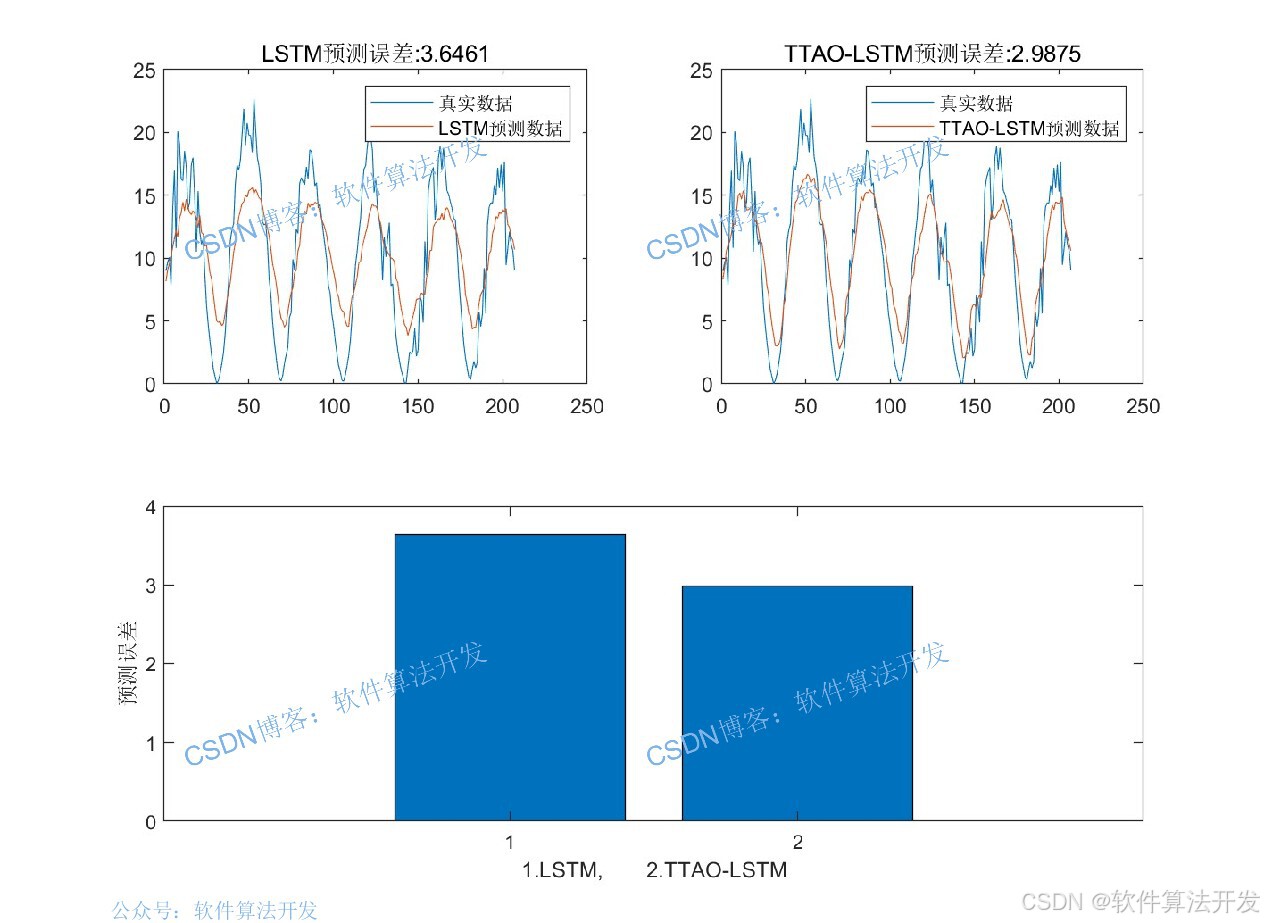
3.部分程序
% 定义全局变量,用于存储训练和测试数据及相关参数
global T_train; % 训练目标数据(原始尺度)
global T_test; % 测试目标数据(原始尺度)
global Pxtrain; % 训练输入数据
global Txtrain; % 训练目标数据(归一化后)
global Pxtest; % 测试输入数据
global Txtest; % 测试目标数据(归一化后)
global Norm_I; % 输入数据归一化参数(用于反归一化)
global Norm_O; % 输出数据归一化参数(用于反归一化)
global indim; % 输入数据维度
global outdim; % 输出数据维度% 加载数据文件data.mat,该文件包含原始数据集
load data.mat
% 调用数据处理函数,对原始数据进行预处理
% 包括划分训练集和测试集、数据归一化等操作
[T_train,T_test,Pxtrain,Txtrain,Pxtest,Txtest,Norm_I,Norm_O,indim,outdim]=func_process(dat);% 定义优化算法的参数范围
low = 5; % 搜索空间下界(优化参数最小值)
high = 100; % 搜索空间上界(优化参数最大值)
dim = 1; % 优化维度(待优化参数的数量)
Tmax = 25; % 最大迭代次数
Npop = 10; % 种群大小(每次迭代的个体数量)N=floor(Npop/3); % Initialize N/3 individuals.
X1=rand(N,dim).*(high-low)+low;
..................
1144.算法理论概述
4.1 TTAO优化算法理论
三角测量拓扑特征提取的核心思想是:将一维时间序列划分为多个局部窗口,通过“三角测量” 机制计算每个窗口内数据点的相对关联度,构建局部拓扑关系图,再从拓扑图中提取表征局部波动、趋势的特征向量。该模块突破传统LSTM仅依赖时序顺序提取特征的局限,通过拓扑结构量化数据点间的非线性关联,增强对局部特征的刻画能力。
拓扑聚合优化模块的作用是:将局部拓扑特征矩阵F中的分散特征,按时间序列的全局拓扑关系(如相邻窗口的特征关联性、全局趋势一致性)进行聚合,生成全局拓扑特征向量,避免传统 LSTM中局部特征孤立传递导致的信息丢失问题。该模块采用 “分层注意力聚合” 机制,先计算窗口间的关联权重,再通过加权求和实现特征融合。
4.2 TTAO优化LSTM网络模型
通过动态调整网络层数(M=2~100),并在各层融入拓扑聚合特征,优化门控机制与细胞状态更新逻辑。层数自适应规则:序列复杂度越高(如波动频率高、非线性强),层数越多;序列平稳时采用较少层数。
以LSTM在训练集上的预测误差作为适应度函数,采用均方根误差,公式为:
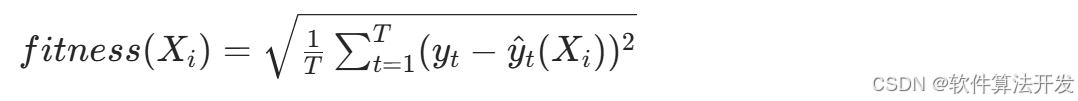
其中,T为训练集样本数, yt为t时刻真实值, y^ t (Xi ) 为基于个体 Xi的LSTM预测值。
TTAO-LSTM以“LSTM预测误差最小”为目标,通过TTAO优化LSTM的关键超参数(如隐藏层神经元数n)。
5.完整程序
VVV
关注后手机上输入程序码:114
