当前位置：首页 > news >正文

LeetCode算法日记 - Day 54: 二叉树的所有路径、全排列

news 2025/9/27 7:31:04

1. 二叉树的所有路径

1.1 题目解析

1.2 解法

1.3 代码实现

2. 全排列

2.1 题目解析

2.2 解法

2.3 代码实现

1. 二叉树的所有路径

https://leetcode.cn/problems/binary-tree-paths/description/

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

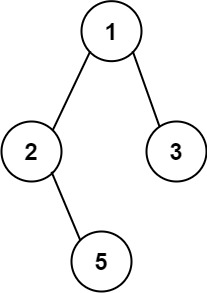
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

提示：

树中节点的数目在范围 [1, 100] 内
-100 <= Node.val <= 100

1.1 题目解析

题目本质
枚举“根 → 叶”的所有路径，并按 "a->b->c" 格式输出。本质是 DFS 路径遍历 + 路径字符串构建。

常规解法
DFS 过程中维护一条“当前路径”。到达叶子就把当前路径收集起来。

问题分析：

共享一个可变缓冲（StringBuilder）需要配合回溯（setLength），否则左右子树会串路径。
每次递归时基于当前前缀新建一个缓冲拷贝，避免回溯。增加对象创建，但本题 N≤100 完全可接受。

思路转折：“复制法”的写法更直观、能避免回溯细节：每层构造本层专属的 StringBuilder 拷贝，子调用只读/追加自己的那份。

1.2 解法

算法思想

• DFS自顶向下；到达节点 u 时基于父层路径 path 创建 cur = new StringBuilder(path)，再 cur.append(u.val)。
• 若 u 是叶子，收集 cur.toString()；否则 cur.append("->") 后递归左右子树。
• 不共享缓冲，不需要回溯。

i）维护结果列表 List<String> ans。

ii）递归 dfs(node, path)：path 表示进入 node 前的前缀。

iii）构造 StringBuilder cur = new StringBuilder(path)，并 cur.append(node.val)。

iv）若 node 为叶子：ans.add(cur.toString()) 返回。

v）否则 cur.append("->")，分别调用 dfs(node.left, cur) 与 dfs(node.right, cur)。

易错点

末尾多一个 ->：只在非叶子时追加箭头。
用 cur = path 只是引用赋值，不是拷贝，必须 new StringBuilder(path)。

1.3 代码实现

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {private List<String> ans = new ArrayList<>();public List<String> binaryTreePaths(TreeNode root) {if (root == null) return ans;dfs(root, new StringBuilder());return ans;}private void dfs(TreeNode node, StringBuilder path) {if (node == null) return;// 基于父层前缀复制一份本层专用缓冲StringBuilder cur = new StringBuilder(path);cur.append(node.val);if (node.left == null && node.right == null) {ans.add(cur.toString());return; // 无需回溯}cur.append("->");dfs(node.left, cur);dfs(node.right, cur);}
}

复杂度分析

时间复杂度：O(N + L)，N 为节点数，L 为所有输出路径的字符总长度。
空间复杂度：递归栈 O(H)，同时由于复制法会在每层创建新缓冲，均摊仍受输出规模 L 主导（结果本身不计入临时空间）。

2. 全排列

https://leetcode.cn/problems/permutations/

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同

2.1 题目解析

题目本质
在长度为 n 的互异元素集合上，枚举所有“位置 → 取值”的映射；也就是求 n 个不同数的全排列（规模约 n!），并输出每条长度为 n 的选择序列。

常规解法
逐层确定第 k 个位置：在未使用的元素里任选一个放入路径，直到路径长度为 n。典型做法是 DFS + 回溯，或用字典序 next_permutation 迭代生成。

问题分析：

若不记录“已用元素”，会出现重复或无效分支，复杂度会膨胀到近似 nnn^nnn。
正确做法是“只在未使用元素中搜索”，使搜索树规模精确为 n! 条叶子。
由于每次命中叶子要拷贝一整条路径，整体时间 ≈ 叶子数 × O(n) = O(n·n!)。

思路转折
想要“既不重复也不漏”且高效 → 必须显式维护已使用标记（vis）并回溯保持不变量：返回父层时，path 与 vis 恢复到进入该层前的状态。节奏就是：选它 → 递归 → 撤销（push→dfs→pop；mark→unmark）。

2.2 解法

算法思想

• 第 k 层代表“正在决定第 k 个位置”的取值；
• 在所有 vis[i]==false 的索引 i 中尝试：push(nums[i]); vis[i]=true; 递归到下一层；
• 若 path.size()==n，把 path 的拷贝加入结果；
• 递归返回时 pop 并 unmark，保证状态回到进入本层前。

i）准备：result（答案），path（当前路径），vis[n]（已用标记）。

ii）入口：调用 dfs()，当 path.size()==n 时收集答案并返回。当 path.size()==n 成立时，相当于遍历到了二叉树的叶子结点。

iii）枚举：循环 i=0..n-1，跳过 vis[i]==true。

iv）选择：path.add(nums[i])，vis[i]=true。

v）下潜：递归 dfs() 决定下一位置。

vi）撤销：path.remove(path.size()-1)，vis[i]=false。

易错点

叶子处必须拷贝：new ArrayList<>(path)，否则后续回溯会改掉已加入的结果。
remove 按下标删除：remove(path.size()-1)，避免与按值删除重载混淆。
vis[i]=true/false 的顺序要与 add/pop 对应，返回时状态必须完全还原。
若存在重复数字需去重（本题已保证互异，否则要排序 + 同层去重）。

2.3 代码实现

class Solution {List<List<Integer>> result;List<Integer> path;boolean[] vis;public List<List<Integer>> permute(int[] nums) {int n = nums.length;result = new ArrayList<>();path = new ArrayList<>(n);vis = new boolean[n];dfs(nums);return result;}private void dfs(int[] nums) {if (path.size() == nums.length) {           // 命中叶子：收集一条排列result.add(new ArrayList<>(path));      // 一定要拷贝return;}for (int i = 0; i < nums.length; i++) {if (vis[i]) continue;                   // 已用跳过path.add(nums[i]);                      // 选择vis[i] = true;                          // 占用dfs(nums);                              // 下探下一位置path.remove(path.size() - 1);           // 撤销选择vis[i] = false;                         // 释放占用}}
}

复杂度分析