当前位置：首页 > news >正文

代码随想录第16天|找树左下角的值、路径总和

news 来源：原创 2025/5/20 6:35:05

参考资料：代码随想录

513.找树左下角的值

力扣题目链接(opens new window)

给定一个二叉树，在树的最后一行找到最左边的值。

示例 1:

513.找树左下角的值

示例 2:

513.找树左下角的值1

思路分析

答案如下

class Solution {
public:
    // 递归怎么去设计
    int maxDepth = INT_MIN;
    int result;
    void traversal(TreeNode* root, int depth) { // 递归函数，用于遍历二叉树
        if(root -> left == NULL && root ->right == NULL) { 
            if(depth > maxDepth) { 
                maxDepth = depth;
                result = root -> val;
            }
            return; // 返回上一层递归
        }
        if(root -> left) { 
            depth++;
            traversal(root -> left, depth);
            depth--; // 回溯
        }
  
        if(root -> right) { 
            depth++;
            traversal(root->right, depth);
            depth--; // 回溯
        }
        return;
    }
    int findBottomLeftValue(TreeNode* root) {
        // 首先判断是不是最底层，然后判断是不是最左边。
        // 假设二叉树至少有一个节点。
        traversal(root , 0);
        return result;
    }
};

怎么理解这段代码

        if(root -> right) { 
            depth++;
            traversal(root->right, depth);
            depth--; // 回溯
        }

depth++;发现存在右子节点后，深度+1
traversal(root->right, depth);depth--; // 回溯右子树递归调用返回时，说明已经完成了对右子树的遍历。所以深度需要-1来回溯到上一次，便于处理其他部分，比如左子树。

用层序遍历实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {//接收一个指向树节点（TreeNode）的指针 root，返回值类型为 int。
        queue<TreeNode*> que;
        if(root != NULL) que.push(root);
        int result = 0;
        while(!que.empty()) { 
            int size = que.size();
            for(int i = 0; i < size; i++) {  // 为什么这里size不用-1 -- size表示当前层的所有节点
                TreeNode* node = que.front(); // 获取队列（queue）的队首元素
                que.pop();
                if( i == 0) result = node -> val; // 如果是当前层的第一个节点，就将其赋给result,因为按层次遍历顺序，每层第一个节点就是最左边的节点。
                if(node -> left) que.push(node -> left);
                if(node -> right) que.push(node -> right);
            }
        }
        return result;
    }
};

112. 路径总和

力扣题目链接(opens new window)

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例: 给定如下二叉树，以及目标和 sum = 22，

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

第一次写的问题

为什么要用bool值来返回？

因为要判断当前target的值是否存在。

代码实现

class Solution {
private:
// 为什么递归函数的返回值要用布尔值。
    bool traversal(TreeNode* cur, int count) {
        if(!cur->left && !cur->right && count == 0) return true;
        if(!cur->left  && !cur->right) return false; // 遇到叶子节点直接返回，叶子节点的特点是没有左右节点。

        if(cur->left) { 
            count -= cur->left->val; // 递归
            if(traversal(cur -> left, count)) return true;
            count+= cur -> left -> val;
        }
        if(cur ->right) { 
            count -= cur -> right -> val;
            if(traversal(cur -> right, count)) return true;
            count+=  cur ->right -> val;
        }
        return false;
    }
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == NULL) return false;
        return traversal(root, targetSum - root->val);
    }
};

// 求和和前序遍历/递归有什么关系?

写完代码后有几个问题

如何确认终止条件？
- 让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。如果cout == 0 且找到目标值的话说明找到了目标和。
- 如果遍历到了叶子节点，count不为0，就是没找到。

113路径总和||

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

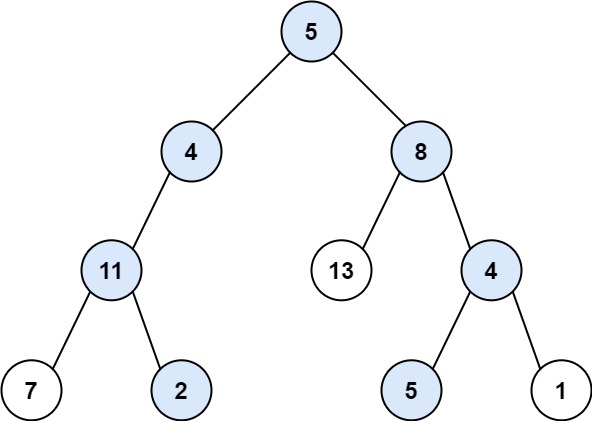
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

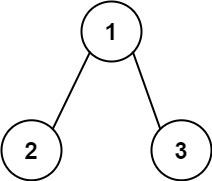
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

第一次写的问题

使用的是一个二维数组来写的，需要去返回路径，那递归函数的返回值和参数是什么呢
- 递归函数的返回值通常设为 void，因为我们的目的是在遍历过程中收集满足条件的路径并存储到结果数组中，而不是通过返回值传递信息。返回的参数有当前节点指针，剩余的目标和，当前路径，结果二维数组。void dfs(TreeNode* node, int remainingSum, vector<int>& path, vector<vector<int>>& result)

结束条件写什么？

if(node == nullptr) { 
            return;
        }

题目解析

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    void dfs(TreeNode* node, int remainingSum, vector<int>& path, vector<vector<int>>& result) { 
        if(node == nullptr) { 
            return;
        }
        path.push_back(node -> val);
        // 更新剩余的和
        remainingSum -= node -> val;
        if(node->left == nullptr && node ->right == nullptr && remainingSum == 0) { 
            result.push_back(path);
        }
        // 递归左子树
        dfs(node ->left, remainingSum, path, result);
        dfs(node -> right, remainingSum, path, result);

        path.pop_back();
    }
public:
    
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        vector<vector<int>> result;
        vector<int> path;
        dfs(root, targetSum, path ,result);
        return result;
    }
};

看完解析后的问题

这些参数dfs(TreeNode* node, int remainingSum, vector<int>& path, vector<vector<int>>& result) 的设置有什么讲究吗？
- 通过传递节点指针，递归函数可以方便的访问左右节点，实现对整个二叉树的遍历。node为空的时候，表示已经达到空节点，递归终止。
- 维护 remainingSum，可以在遍历到叶子节点时，快速判断当前路径上的节点值之和是否等于目标和，如果怕remainingSum为0,说明满足条件。
- 引用传递 path 可以避免在递归调用过程中频繁复制路径数组，提高性能。通过动态更新 path，可以方便地记录和回溯路径
- vector<vector<int>>& result递归函数可以直接修改外部的结果数组，将满足条件的路径添加到其中