栈的学习——逆波兰表达式(RPN)
逆波兰表达式
地址:https://leetcode.cn/problems/evaluate-reverse-polish-notation/
为了让打大家好理解一点,博主这里选择与普通算式做一个对比,来方便大家理解。
逆波兰表达式
前缀表达式(Polish Notation, PN):运算符写在操作数前面。
例:中缀 3 + 4 → 前缀 + 3 4
后缀表达式(Reverse Polish Notation, RPN):运算符写在操作数后面。
例:中缀 3 + 4 → 后缀 3 4 +
中缀表达式:运算符写在两个操作数中间。
例:3 + 4
👉 名字来源:最早由波兰逻辑学家 卢卡西维茨 (Lukasiewicz) 提出,波兰表示法是前缀运算(+ 3 4),逆波兰就是后缀(3 4 +)。
2️⃣ 三种表达式对照示例
示例 1
中缀:3 + 4 * 5
前缀:+ 3 * 4 5
后缀:3 4 5 * +
示例 2
中缀:(a + b) * (c - d)
前缀:* + a b - c d
后缀:a b + c d - *
示例 3
中缀:a + b * c - d / e
前缀:- + a * b c / d e
后缀:a b c * + d e / -

选择题快速计算方法
后缀表达式:
-
你根据加减乘除的算法顺序,在每一个要计算的表达式加上括号
-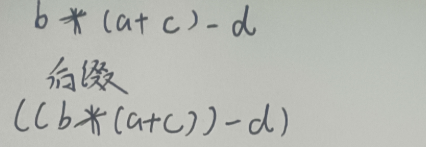
-
然后你把这个每一个括号里的运算符往后一个要计算的运算括号外的右边移动
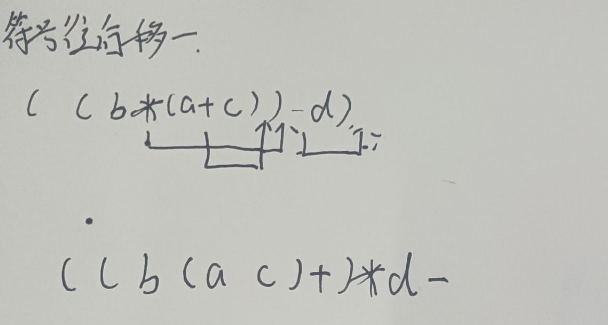
-
最后,把括号去掉就是中缀表达式转换为后缀表达式
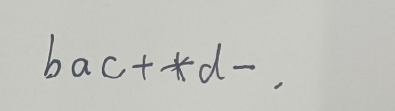
前缀表达式: -
你根据加减乘除的算法顺序,在每一个要计算的表达式加上括号
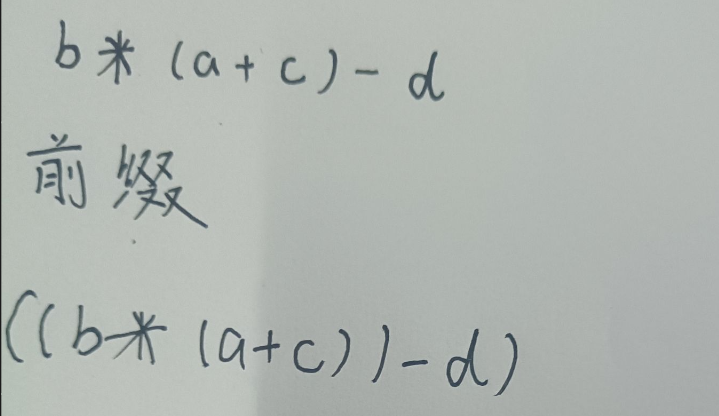
-
然后你把这个每一个括号里的运算符往前一个要计算的运算括号里移动到左边去,比如-b 这个运算括号区域内是最外侧,所以把这个-号移动到最外侧的括号的外边,也就是现在第一个的字符
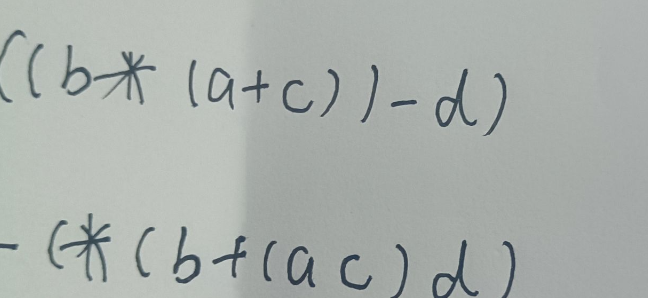
-
最后,把括号去掉就是中缀表达式转换为前缀表达式
从代码层面解决这个问题
思路讲解
-
用一个栈保存“尚未参与计算的操作数”。
-
从左到右遍历 tokens:
- 遇到数字:压栈(先不算)。
-遇到运算符:
-先 pop 出右操作数 p1,再 pop 出左操作数 p2;
-计算 p2 op p1;
-把结果转成字符串压回栈。
- 遇到数字:压栈(先不算)。
-
遍历结束后,栈中只剩最后一个字符串数字,把它 parseInt 返回。
-
关键:RPN 的“谁先算”由位置决定,不用括号;出栈顺序固定保证了非交换运算(减、除)的方向正确。
1.判断是否是运算符
2.判断完完后,如果是运算符,我们取栈里顶部的数字,根据不同的运算符进行计算,然后在把这个进行完计算的数,把这个获取的数重新压入栈中。
3.如果不是运算符的话,说明是数字,我们直接压入栈中,等待计算即可
4.循环下去,我们就可以得到最后一个结果,最后留下来的就是计算的结果
这个方法是用的字符串的,这个是我第一次做出来思路,不过给复杂化了,思路没有问题
//这个方法是用的字符串的,这个是我第一次做出来思路,不过给复杂化了,思路没有问题
class Solution {public int evalRPN(String[] tokens) {Stack<String> stack = new Stack<>();//首先创建一个栈for(String x : tokens) {
if(isOperator(x)){//true 说明是运算符//注意:先弹出的是要放发到右运算位的Integer p1 = Integer.valueOf(stack.pop());//右操作数Integer p2 = Integer.valueOf(stack.pop());//左操作数//切记先出栈的要放到右运算位Integer p3 = 0;switch (x) {case "+":p3 = p2+p1;break;case "-":p3 =p2 - p1;break;case "*":p3 =p2 * p1;break;case "/" :p3 =p2 / p1;break;}stack.push(String.valueOf(p3));}else {//如果说是数字stack.push(x);}}return Integer.parseInt(stack.pop());}public boolean isOperator(String x) {if(x.equals("+" ) || x.equals ("-") || x.equals("/") || x.equals( "*")){return true;}return false;}
}
接下来我给大家在来一个 用Integer 的方法,刚刚那个方法一直在来回转换,博主没有转过这个弯,希望对大家有所帮助。
for (String x : tokens) {if (isOperator(x)) {Integer p1 = Integer.valueOf(stack.pop()); // 右操作数Integer p2 = Integer.valueOf(stack.pop()); // 左操作数Integer p3 = 0;switch (x) {case "+": p3 = p2 + p1; break;case "-": p3 = p2 - p1; break; // 左 - 右case "*": p3 = p2 * p1; break;case "/": p3 = p2 / p1; break; // 左 / 右(int 向0取整)}stack.push(String.valueOf(p3));} else {stack.push(x); // 数字先存着}
}
return Integer.parseInt(stack.pop());//方法:判断是不是运算符
public boolean isOperator(String x) {return x.equals("+") || x.equals("-") || x.equals("/") || x.equals("*");
}1.同样是判断是否是运算符
2.判断完完后,如果是运算符,我们取栈里顶部的数字,根据不同的运算符进行计算,然后在把这个进行完计算的数,把这个获取的数重新压入栈中。
3.如果不是运算符的话,说明是数字,我们直接压入栈中,等待计算即可
4.循环下去,我们就可以得到最后一个结果,最后留下来的就是计算的结果
