当前位置：首页 > news >正文

离散时间信号和系统的频域分析

news 2025/9/26 14:08:13

离散时间信号和系统的频域分析

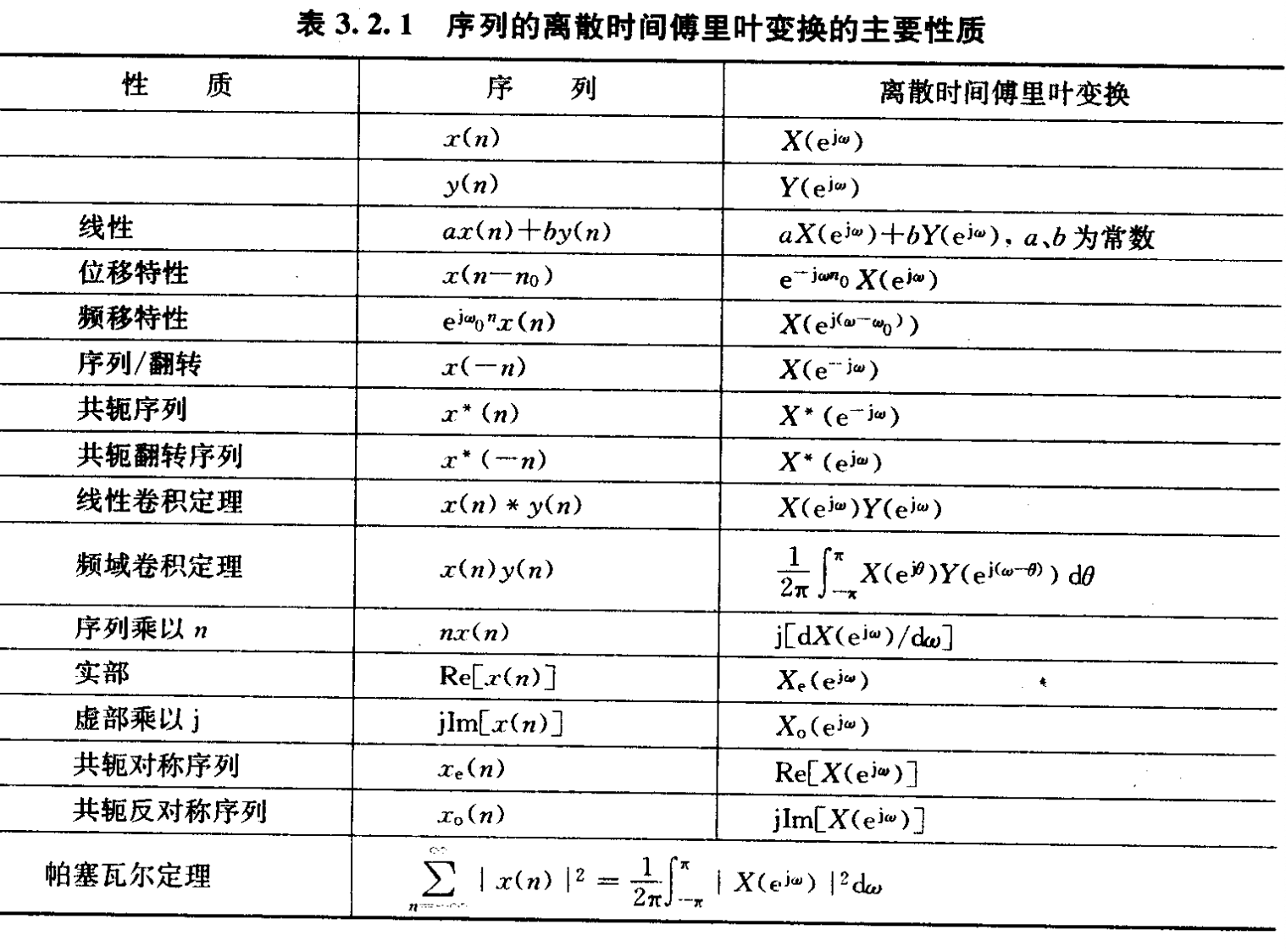
序列的离散时间傅里叶变换

DTFT 的结果就是一个以 连续频率变量 ω 为自变量的 连续函数：

$X(e^{j\omega})=\sum_{n=-\infty}^{\infty} x[n]\,e^{-j\omega n},\quad \omega\in\mathbb{R}$

定义域：整个实轴 ( \omega \in (-\infty,\infty) )
值域：复数域 ( \mathbb{C} )
周期性：( X(e^{{j(\omega+2\pi)})=X(e}{j\omega}) )，所以通常只画 ( [0,2\pi) ) 或 ( [-\pi,\pi) ) 区间

因此，DTFT 把离散时域信号映射成一条连续的“频谱曲线”。

IDTFT（离散时间傅里叶逆变换）同样工作在连续频域：

$x[n]=\frac{1}{2\pi}\int_{-\pi}^{\pi}X(e^{j\omega})\,e^{j\omega n}\,d\omega,\quad n\in\mathbb{Z}$

输入：连续周期函数 (X(e^{j\omega}))
输出：离散序列 (x[n])

所以 IDTFT 的积分变量 ω 是连续的，结果才是离散的时域样本。
一句话：IDTFT 把“连续频谱”变回“离散时域”。

DTFT 的常用性质

统一记号：
$x[n]\;\xleftrightarrow{\text{DTFT}}\;X\!\left(e^{j\omega}\right)$
所有性质均直接由定义式
$X\!\left(e^{j\omega}\right)=\sum_{n=-\infty}^{\infty}x[n]\,e^{-j\omega n}$

周期性（Periodicity）
$X\!\left(e^{j(\omega+2\pi)}\right)=X\!\left(e^{j\omega}\right)$
记忆：离散时域 → 频域必然 2π 周期。

线性（Linearity）
$a\,x_{1}[n]+b\,x_{2}[n]\;\xleftrightarrow{\text{DTFT}}\;a\,X_{1}\!\left(e^{j\omega}\right)+b\,X_{2}\!\left(e^{j\omega}\right)$
记忆：变换是求和与积分，自然满足叠加。

时移（Time Shift）
$x[n-n_{0}]\;\xleftrightarrow{\text{DTFT}}\;e^{-j\omega n_{0}}\,X\!\left(e^{j\omega}\right)$
记忆：延迟 n₀ 只在频域乘一个“线性相位”因子。

频移（Frequency Shift / Modulation）
$e^{j\omega_{0}n}\,x[n]\;\xleftrightarrow{\text{DTFT}}\;X\!\left(e^{j(\omega-\omega_{0})}\right)$
记忆：时域乘复指数 = 频谱整体搬移 ω₀。

序列乘以 n（频域微分）
$n\,x[n]\;\xleftrightarrow{\text{DTFT}}\;j\,\frac{dX\!\left(e^{j\omega}\right)}{d\omega}$
记忆：n 相当于“对 ω 求导”再乘 j。

共轭序列（Conjugation）
$x^{*}[n]\;\xleftrightarrow{\text{DTFT}}\;X^{*}\!\left(e^{-j\omega}\right)$
记忆：时域共轭 → 频域共轭并“反转频率”。

反转（Time Reversal）
$x[-n]\;\xleftrightarrow{\text{DTFT}}\;X\!\left(e^{-j\omega}\right)$

卷积（Convolution）
$x[n]*h[n]\;\xleftrightarrow{\text{DTFT}}\;X\!\left(e^{j\omega}\right)H\!\left(e^{j\omega}\right)$

DTFT 的对称性（Symmetry Properties）
把序列拆成共轭对称/反对称部分：

共轭对称序列：
$x_{\text{cs}}[n]=\tfrac{1}{2}\bigl(x[n]+x^{*}[-n]\bigr) \;\xleftrightarrow{\text{DTFT}}\; \text{Re}\!\left\{X\!\left(e^{j\omega}\right)\right\}$

共轭反对称序列：
$x_{\text{ca}}[n]=\tfrac{1}{2}\bigl(x[n]-x^{*}[-n]\bigr) \;\xleftrightarrow{\text{DTFT}}\; j\,\text{Im}\!\left\{X\!\left(e^{j\omega}\right)\right\}$

特别地，若 x[n] 为实序列，则

实部偶对称： $Re{X(ejω)}=Re{X(e−jω)}\text{Re}\{X(e^{j\omega})\}=\text{Re}\{X(e^{-j\omega})\}$
虚部奇对称： $Im{X(ejω)}=−Im{X(e−jω)}\text{Im}\{X(e^{j\omega})\}=-\text{Im}\{X(e^{-j\omega})\}$
幅度偶对称： $∣X(ejω)∣=∣X(e−jω)∣|X(e^{j\omega})|=|X(e^{-j\omega})|$
相位奇对称： $arg⁡{X(ejω)}=−arg⁡{X(e−jω)}\arg\{X(e^{j\omega})\}=-\arg\{X(e^{-j\omega})\}$

记忆：实信号 ⇨ 频谱“共轭对称”。

时域卷积定理（Convolution in Time）
$x[n]*h[n]=\sum_{k=-\infty}^{\infty}x[k]\,h[n-k]\;\xleftrightarrow{\text{DTFT}}\;X\!\left(e^{j\omega}\right)H\!\left(e^{j\omega}\right)$
记忆：时域卷积 ⇨ 频域相乘（最常用，滤波器设计核心）。

频域卷积定理（Convolution in Frequency / 调制定理）
$x[n]\,h[n]\;\xleftrightarrow{\text{DTFT}}\;\frac{1}{2\pi}\Bigl[X\!\left(e^{j\omega}\right)\circledast H\!\left(e^{j\omega}\right)\Bigr]=\frac{1}{2\pi}\int_{-\pi}^{\pi}X\!\left(e^{j\theta}\right)H\!\left(e^{j(\omega-\theta)}\right)d\theta$
记忆：时域相乘 ⇨ 频域做周期卷积并除以 2π（调制/窗函数必用）。

帕塞瓦尔定理（Parseval / 能量守恒）
$\sum_{n=-\infty}^{\infty}x[n]\,y^{*}[n]=\frac{1}{2\pi}\int_{-\pi}^{\pi}X\!\left(e^{j\omega}\right)Y^{*}\!\left(e^{j\omega}\right)d\omega$
特别地，当 y[n]=x[n] 时，得到能量公式
$E_{x}=\sum_{n=-\infty}^{\infty}|x[n]|^{2}=\frac{1}{2\pi}\int_{-\pi}^{\pi}\bigl|X\!\left(e^{j\omega}\right)\bigr|^{2}d\omega$
记忆：时域能量 = 频域能量（只差 2π 归一化），|X(e^{jω})|² 称为能量谱密度。