当前位置：首页 > news >正文

力扣995. K 连续位的最小翻转次数

news 2025/9/26 7:11:57

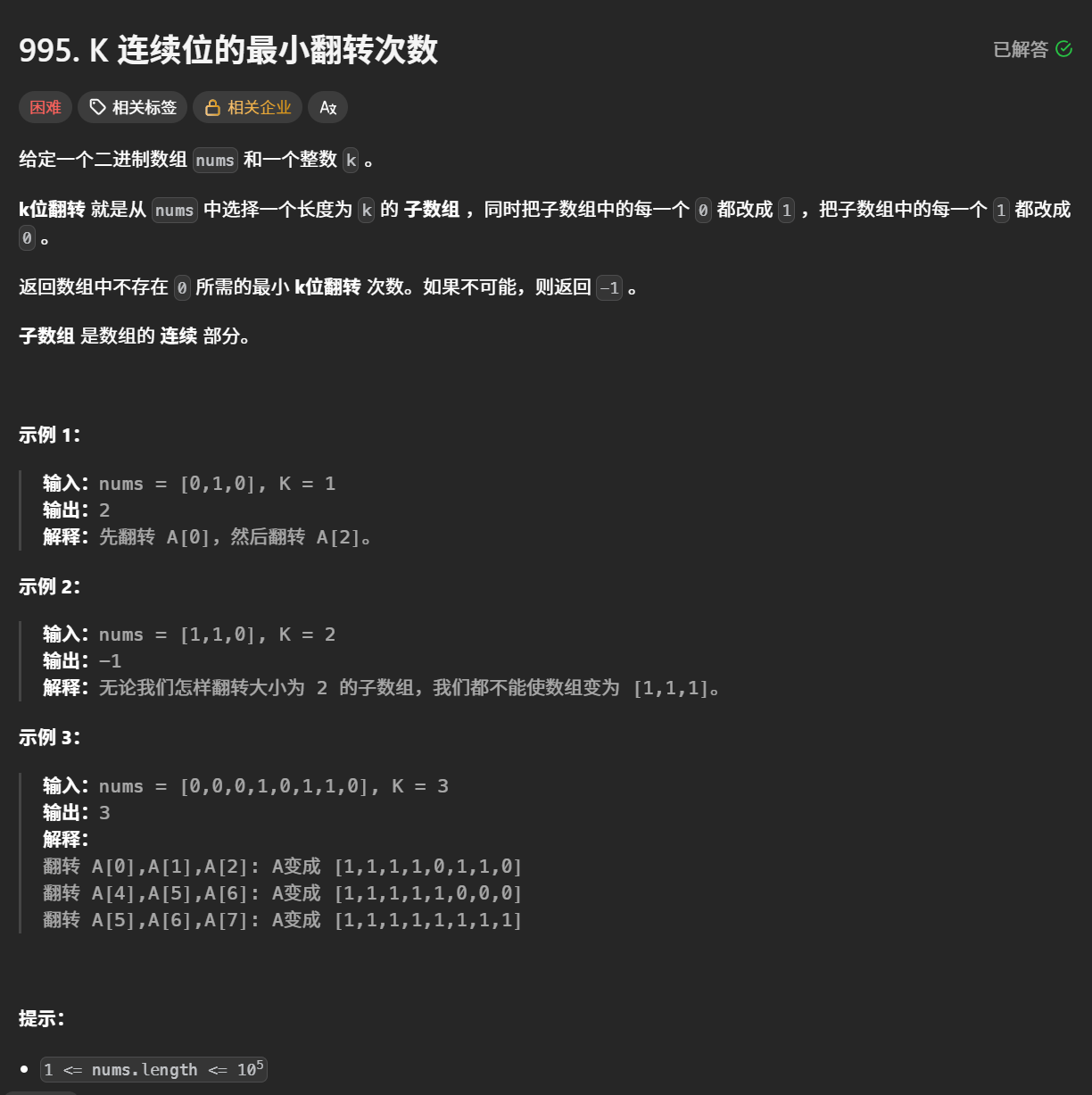
在这里插入图片描述

题目大意是给出了一个都是01的数组，现在让我们反转它的长度为k的子数组，使得所有的数组中都是1，找出最小的反转次数。
首先，我们要想的是，怎么样反转，才会使反转次数最小呢，我们可以选择每一次反转一个k长度的子数组，其中尽可能多的包含0元素，但不可避免的会反转错误的元素，比如一个子数组中既有0，又有1，我们反转的时候不可避免的错误的把1反转为0，那么我们还要把误反转的改回来，这毫无疑问会增加反转次数，特别是1在0的前面，因此我们最好的是在反转的子数组中0是处于第一个位置，这样即使子数组中有1的存在，我们也会往后继续走，把误反转的当作本身是0的，继续反转，因此，我们发现，每遇到0就进行以该位置（i）为起点（i，i+k-1）进行反转，即使有1被翻了，可以继续把把误反转的当作本身是0的这种贪心的翻法是最优的。
如果我们不是用这种贪心的翻法，而是把1放在子数组的前面位置，那么即使子数组后面成功的把0反转为1，我们还要回过头来再去修改被误翻的元素，而在处理误翻的元素的时候又有可能处理到原来已经翻好的元素，这毫无疑问不是最优的。
一句话就是：遇到 0 就翻从它开始的 k 位，这是最优策略，因为误翻的 1 可以顺序修正，而不必回头重复翻已经处理过的元素。
因此，我们选择了一遇到0，就把该位置（i）为起点（i，i+k-1）进行反转，但这样暴力的枚举的时间复杂度是O（n*k）超过10^8，需要想办法进行优化，
我们发现对该位置（i）为起点（i，i+k-1）进行反转这种是对区间进行连续操作，因此可以用差分来优化。
即当翻到一个0的时候，对该位置进行差分标记，表示在i，i+k-1的所有位置都进行了一次反转，一个位置的元素值+反转的次数如果是偶数，那么就会变成0，如果是奇数就为1.
完整代码如下：

class Solution {
public:int minKBitFlips(vector<int>& nums,int k) {int n=nums.size();int ans=0;int f=0;vector<int> d(n+1,0);for(int i=0;i<nums.size();i++){//更新反转次数f+=d[i];if((nums[i]+f)%2==0){if(i+k>n){return -1;}ans++;f++;d[i+k]--;} }return ans;}
};