【Leetcode hot 100】124.二叉树中的最大路径和

问题链接

124.二叉树中的最大路径和

问题描述

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

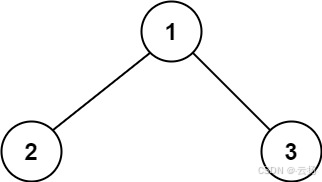
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

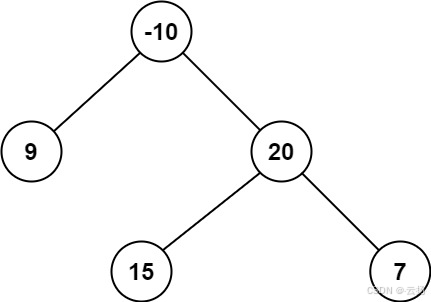
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

• 树中节点数目范围是 [1, 3 * 10^4]
• -1000 <= Node.val <= 1000

问题解答

核心思路

二叉树的最大路径和问题，关键在于区分两种路径贡献：

1. 可向上传递的贡献：以当前节点为终点，路径只能延伸到父节点（即只能选左子树或右子树中的一条支路，避免路径分叉）。
2. 不可向上传递的路径：以当前节点为中间节点，路径覆盖左子树、当前节点、右子树（这种路径无法延伸到父节点，但可能是全局最大路径）。

解决方案采用 深度优先搜索（DFS）：

• 用递归计算每个节点的「可向上传递贡献」。
• 用一个全局变量记录遍历过程中遇到的「不可向上传递路径」的最大值。

完整Java代码

class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {// 全局变量：记录最大路径和（初始化为最小整数，应对全负节点场景）private int maxSum = Integer.MIN_VALUE;public int maxPathSum(TreeNode root) {// 启动DFS，计算每个节点的贡献dfs(root);// 返回全局最大路径和return maxSum;}/*** 递归函数：计算以当前节点为终点的「可向上传递贡献」* @param node 当前遍历的节点* @return 以当前节点为终点，向上传递的最大贡献值*/private int dfs(TreeNode node) {// 边界条件：空节点无贡献，返回0if (node == null) {return 0;}// 计算左子树的贡献：若为负数则舍弃（取max(0, 左贡献)）int leftGain = Math.max(0, dfs(node.left));// 计算右子树的贡献：同理舍弃负数int rightGain = Math.max(0, dfs(node.right));// 计算「不可向上传递的路径和」（左+当前+右），更新全局最大值int currentPathSum = leftGain + rightGain + node.val;maxSum = Math.max(maxSum, currentPathSum);// 返回「可向上传递的贡献」（选左或右中较大的支路 + 当前节点值）return Math.max(leftGain, rightGain) + node.val;}
}

代码解释

1. 全局变量 maxSum：

   • 初始值设为 Integer.MIN_VALUE，因为节点值可能全为负数（如单节点 -5，最大路径和就是 -5，而非 0）。
   • 每次计算「左+当前+右」的路径和时，与 maxSum 比较并更新。

2. DFS 递归函数 dfs(node)：

   • 空节点处理：返回 0，表示空节点对父节点无贡献。
   • 左/右子树贡献计算：用 Math.max(0, ...) 过滤负贡献（若子树贡献为负，不如不选该子树）。
   • 当前节点的局部最大路径：leftGain + rightGain + node.val，对应「左子树→当前节点→右子树」的路径，无法向上传递，但需参与全局最大值竞争。
   • 返回可传递贡献：Math.max(leftGain, rightGain) + node.val，对应「父节点→当前节点→左子树」或「父节点→当前节点→右子树」的路径，可继续向上延伸。

复杂度分析

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每个节点仅遍历一次。
• 空间复杂度：O(h)，其中 h 是二叉树的高度。递归栈的深度取决于树的高度，平衡树为 O(logn)，链状树为 O(n)。