南京大学 LLM开发基础（二）大语言模型解析 -- 基于HF LlaMA实现的讲解

https://njudeepengine.github.io/llm-course-lecture/2025/lecture4.html#1

嵌入 + 位置掩码 + RMSNorm + 前馈神经网络FFN

作业：手搓多头注意力

目录

1. Input / Positional Embedding

Sinusoidal PE 绝对位置编码

旋转位置编码（Rotary PE）

2. Pytorch 中 tensor 的函数操作

3. Normalization

4. 前馈神经网络 FFN & SwiGLU模块

经典激活函数

Task1 多头注意力 - 多头乘法

1. 输入输出形状：

2. 计算步骤：

3. 代码实现

Task2 多头注意力 - 只算重要性高的 + 梯度

1. 题目要求

2. 重要性筛选 [b, s] -> t

3. 梯度计算

---

1. Input / Positional Embedding

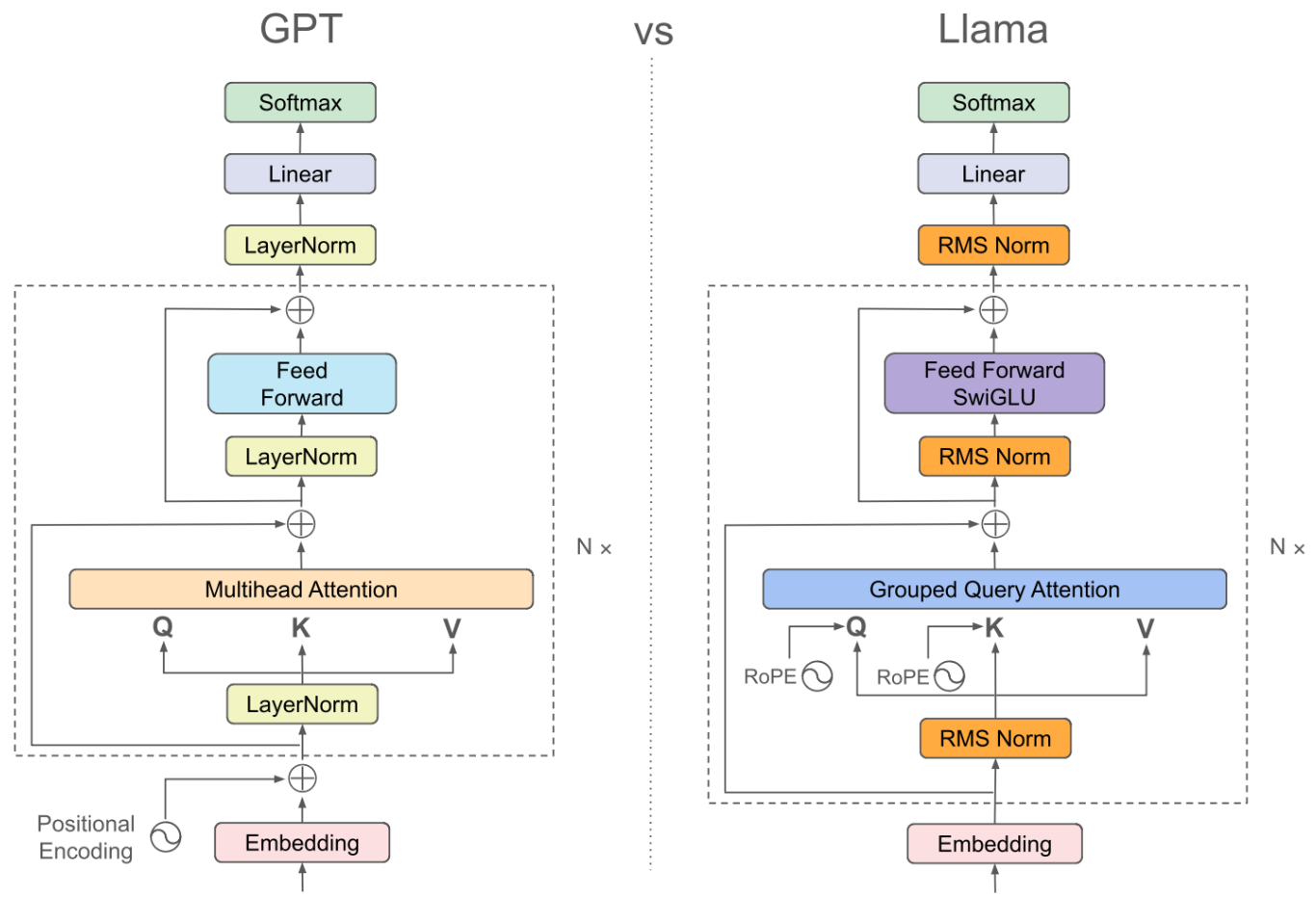
https://tiktokenizer.vercel.app/  不同分词器 embedding后

from transformers import AutoTokenizer
tokenizer = AutoTokenizer.from_pretrained(model_id)

Sinusoidal PE 绝对位置编码

直接在每个token的 embedding 上线性叠加位置编码 xi+pi ，其中pi 为可训练的向量。

经典例：正弦余弦位置编码 第t个词的第i个维度。

不同的维度 根据奇偶正余弦，不同的周期。 不同的 t 对应正余弦值不同 体现位置。

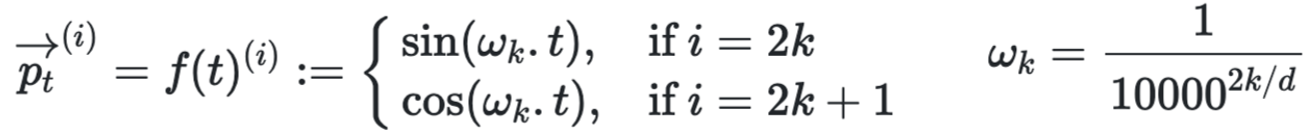
旋转位置编码（Rotary PE）

为每个 “维度对”旋转特定夹角   以下为 2维旋转&n维旋转

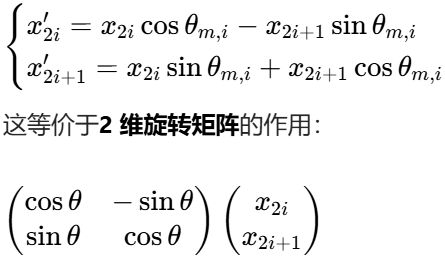
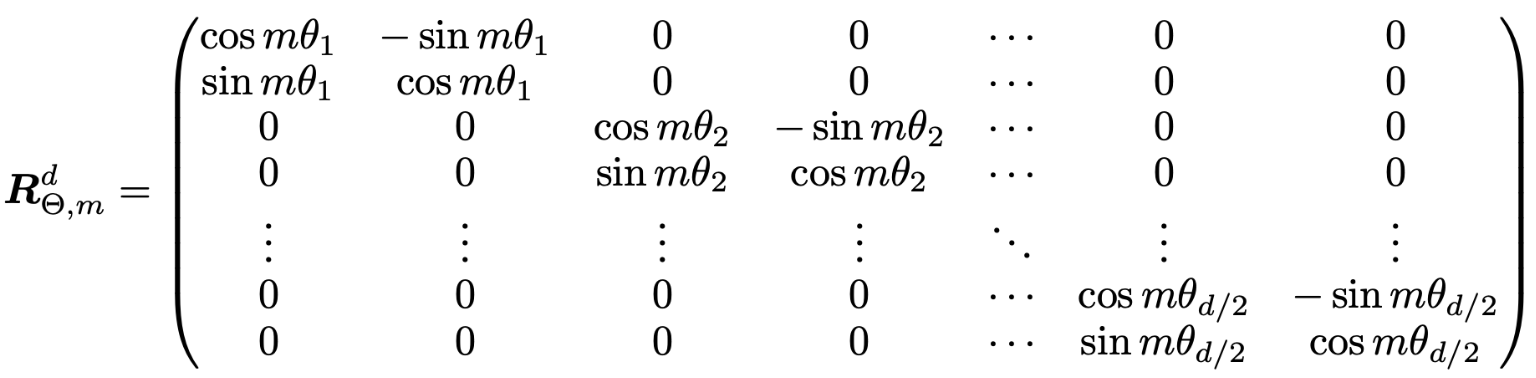
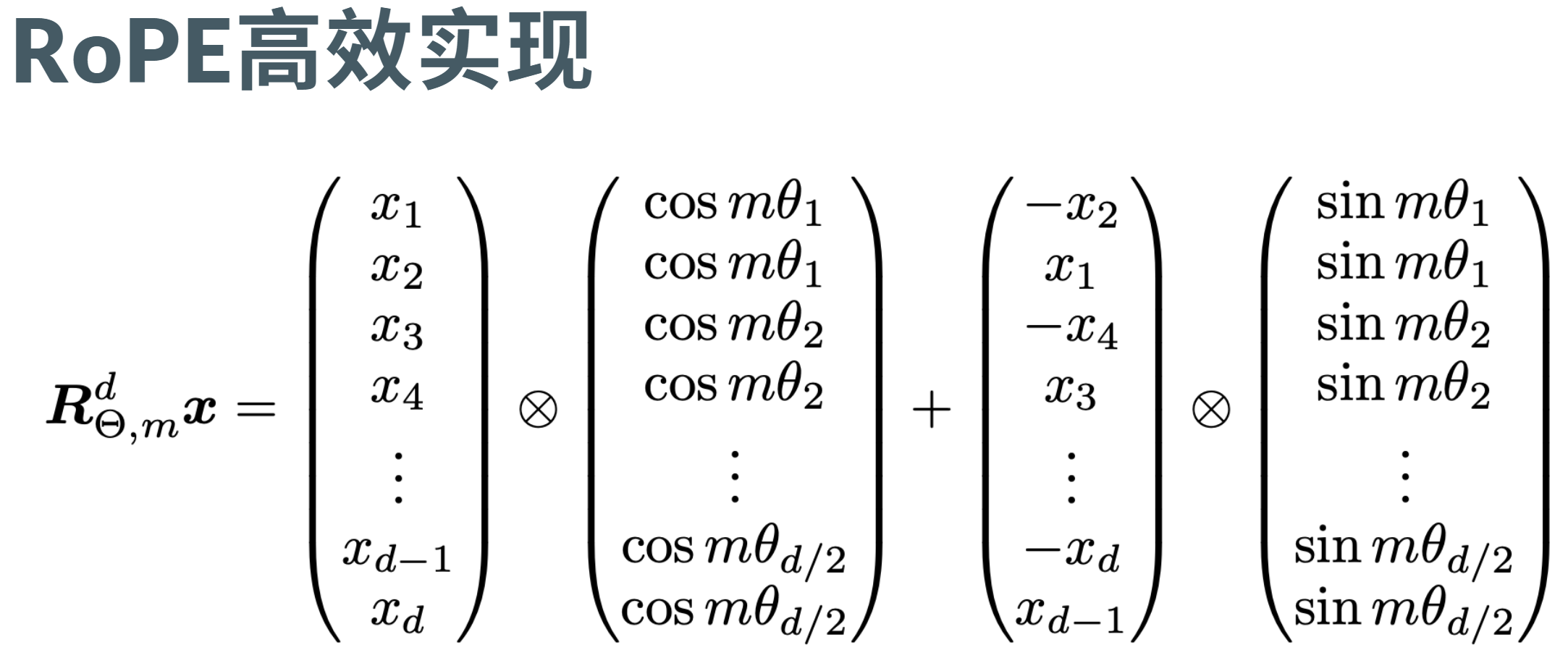
分半 取反 拼接； 变成右边 (-x2, x1, -x4, x3, ...)

def rotate_half(x):"""Rotates half the hidden dims of the input."""x1 = x[..., : x.shape[-1] // 2]  # 取前一半维度 (x1, x3, x5, ...)x2 = x[..., x.shape[-1] // 2 :]  # 取后一半维度 (x2, x4, x6, ...)return torch.cat((-x2, x1), dim=-1)  # 交换并取负：(-x2, x1, -x4, x3, ...)

def apply_rotary_pos_emb(q, k, cos, sin):cos = cos.unsqueeze(unsqueeze_dim)  # 扩展维度以便广播sin = sin.unsqueeze(unsqueeze_dim)  # 扩展维度以便广播# RoPE 核心计算q_embed = (q * cos) + (rotate_half(q) * sin)k_embed = (k * cos) + (rotate_half(k) * sin)

2. Pytorch 中 tensor 的函数操作

https://njudeepengine.github.io/llm-course-lecture/2025/lecture4.html#29

pytorch - tensor-operations

转置 / 维度交换操作

transpose() - 交换两个维度

x = torch.randn(2, 3, 4, 5)
y = x.transpose(1, 3)  # 交换维度1和3
print(x.shape)  # torch.Size([2, 3, 4, 5])
print(y.shape)  # torch.Size([2, 5, 4, 3])

permute() - 按制定顺序 重新排列所有维度

上两者操作会导致 张量不连续；可通过 .contiguous() 恢复连续性。

x = torch.randn(2, 3, 4, 5)
y = x.permute(0, 3, 1, 2)  # 重新排列维度
print(x.shape)  # torch.Size([2, 3, 4, 5])
print(y.shape)  # torch.Size([2, 5, 3, 4])x_contiguous = x_t.contiguous()

形状变换操作：view vs reshape

reshape() 相当于检查连续性版本的 view()

x = torch.randn(2, 3, 4)  # 形状：2×3×4
y = x.view(6, 4)          # 成功：2×3=6x_transposed = x.transpose(0, 1)  # 形状变为：3×2×4y = xx_transposed.view(12, 2) # 报错，因为转置后不连续 if x_transposed.is_contiguous():result = x_transposed.view(12, 2)
else:result = x_transposed.contiguous().view(12, 2)  # 先复制再reshape

移除 / 添加 大小为1的维度

squeeze() - 移除大小为1的维度

x = torch.randn(1, 3, 1, 4)
y = x.squeeze()  # 移除所有大小为1的维度
z = x.squeeze(0)  # 只移除第0维
print(x.shape)  # torch.Size([1, 3, 1, 4])
print(y.shape)  # torch.Size([3, 4])
print(z.shape)  # torch.Size([3, 1, 4])

unsqueeze() - 在指定位置插入大小为1的维度

x = torch.randn(3, 4)
y = x.unsqueeze(0)  # 在第0维插入
z = x.unsqueeze(-1)  # 在最后一维插入
print(x.shape)  # torch.Size([3, 4])
print(y.shape)  # torch.Size([1, 3, 4])
print(z.shape)  # torch.Size([3, 4, 1])

乘法

• torch.matmul() / @: 通用矩阵乘法，支持广播
• torch.bmm(): 批量矩阵乘法，专门用于3D tensor
• torch.mm(): 2D矩阵乘法

• torch.einsum 爱因斯坦求和约定  通过字符串要求格式

        如后面多头中用到的  output = torch.einsum('bshd,hde->bshe', input, weight)

gather 拿 scatter 插

torch.gather() - 按索引收集元素      把对应位置的拿出来

x = torch.tensor([[1, 2, 3],[4, 5, 6],[7, 8, 9]])indices = torch.tensor([[0, 1],[1, 2], [0, 2]])y = torch.gather(x, 1, indices) # 1代表处理每行
# 结果：每行按索引选取对应列的元素
# [[1, 2],   # 第0行：列0=1, 列1=2
#  [5, 6],   # 第1行：列1=5, 列2=6  
#  [7, 9]]   # 第2行：列0=7, 列2=9

torch.scatter_() - 将元素分散到指定位置    插到对应位置

x = torch.zeros(3, 4)
values = torch.randn(3, 2)
indices = torch.tensor([[0, 2], [1, 3], [0, 1]])
x.scatter_(1, indices, values)

detach() 函数：从计算图中分离张量，阻止梯度传播

3. Normalization

使得梯度下降的时候 加速收敛，降低过拟合(overfitting)，增强泛化(generalization)

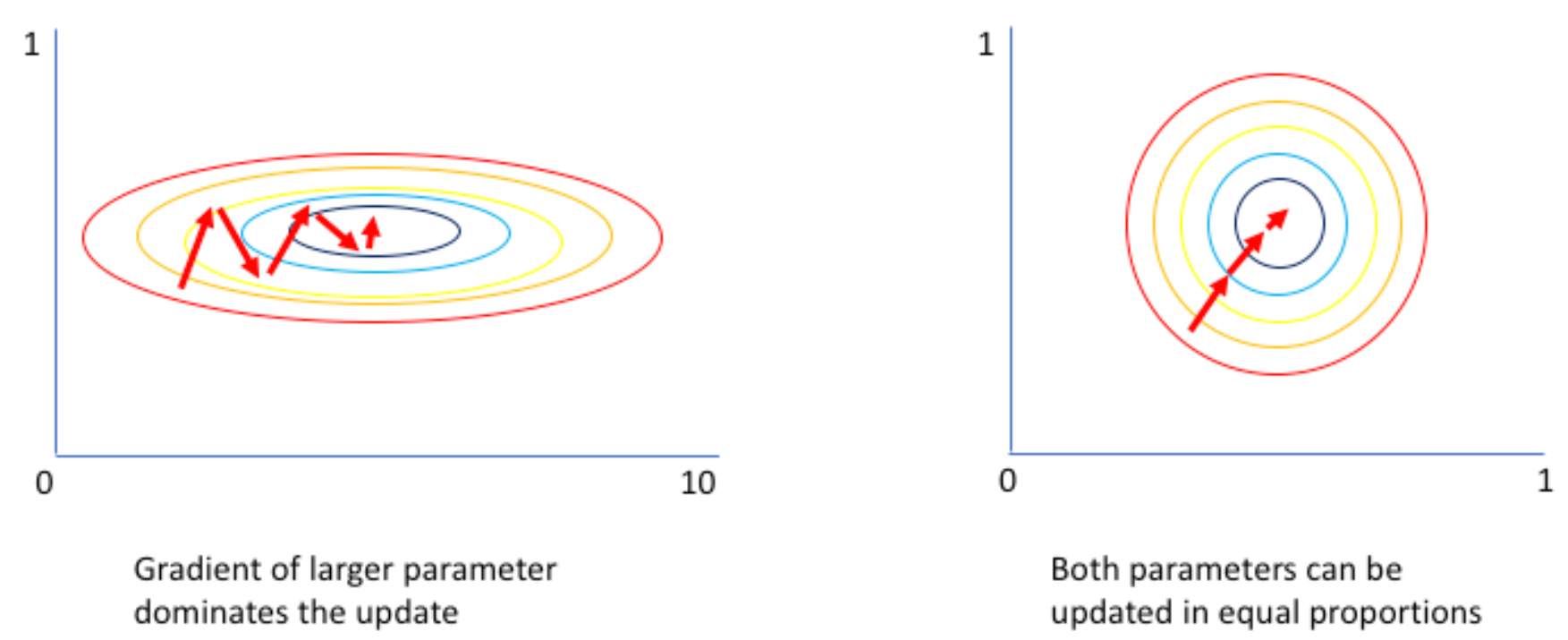
在大模型中，调整数据分布。

• Batch Norm（批归一化）：对每个通道，在整个批次的空间维度（如图像的高、宽）上统计均值和方差。类比：全班学生（批量）的某一门科目（通道）成绩整体归一化。（依赖于batch长度 足够多的batch才能进行 批归一化）

• Layer Norm（层归一化）：对单个样本的所有通道和空间维度统计均值和方差。类比：单个学生的所有科目成绩整体归一化。

• 两个可学习参数 灵活性；但进行求和比较麻烦。

        

             

• Group Normalization（组归一化）：将通道分成若干组，对每个组内的通道在单个样本的空间维度上统计均值和方差。类比：把科目分成 “文科组”“理科组”，对每个组内的科目成绩归一化。

RMSNorm -- Root Mean Square Layer Normalization

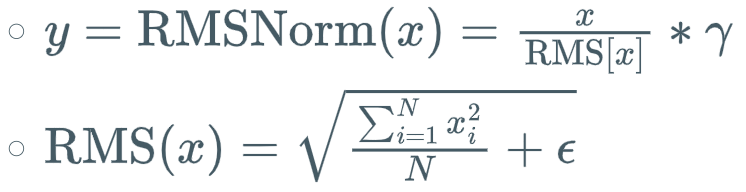
手搓

input =input.to(torch.float32)
variance =input.pow(2).mean(-1,keepdim=True)
hidden_states =input * torch.rsqrt(variance + variance_epsilon)

直接调用 nn.RMSNorm

rms_norm = nn.RMSNorm(normalized_shape=512)# 随机生成一个输入张量 (batch_size=2, seq_len=10, feature_dim=512)
x = torch.randn(2, 10, 512)# 应用RMSNorm
output = rms_norm(x)

4. 前馈神经网络 FFN & SwiGLU模块

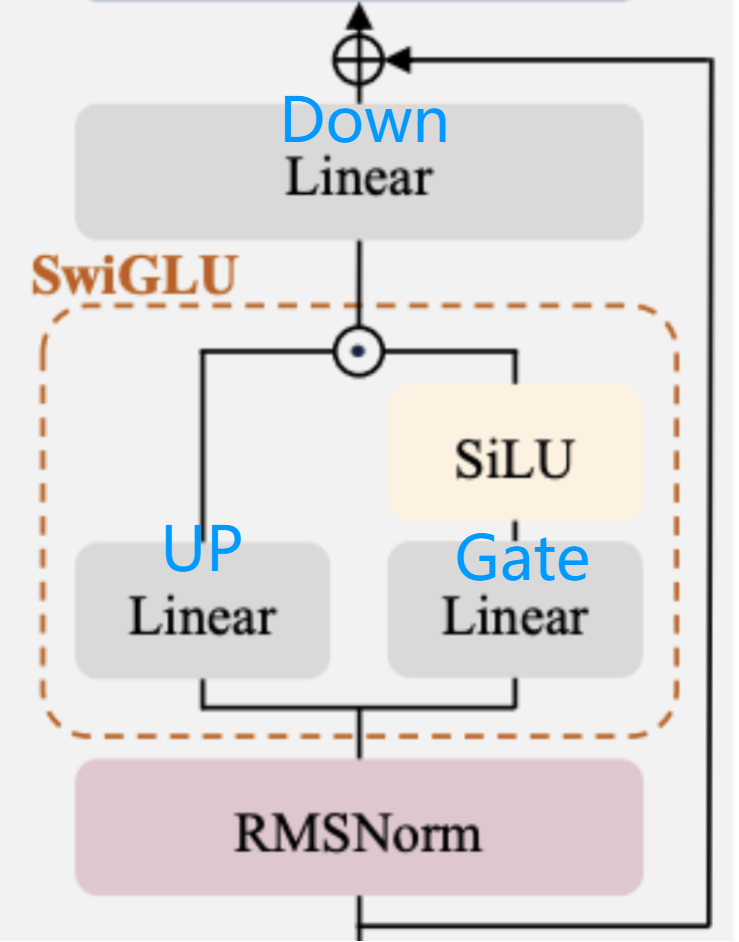    2048  ->  8192  -> 2048

(mlp): LlamaMLP((gate_proj): Linear(in_features=2048, out_features=8192, bias=False)(up_proj): Linear(in_features=2048, out_features=8192, bias=False)(down_proj): Linear(in_features=8192, out_features=2048, bias=False)(act_fn): SiLU()
)

pytorch - SiLU激活函数

上采样 * 门控&激活  -> 下采样 维度回投

down_proj = self.down_proj (self.act_fn(self.gate_proj(x)) * self.up_proj(x) )

经典激活函数

增加模型非线性能力

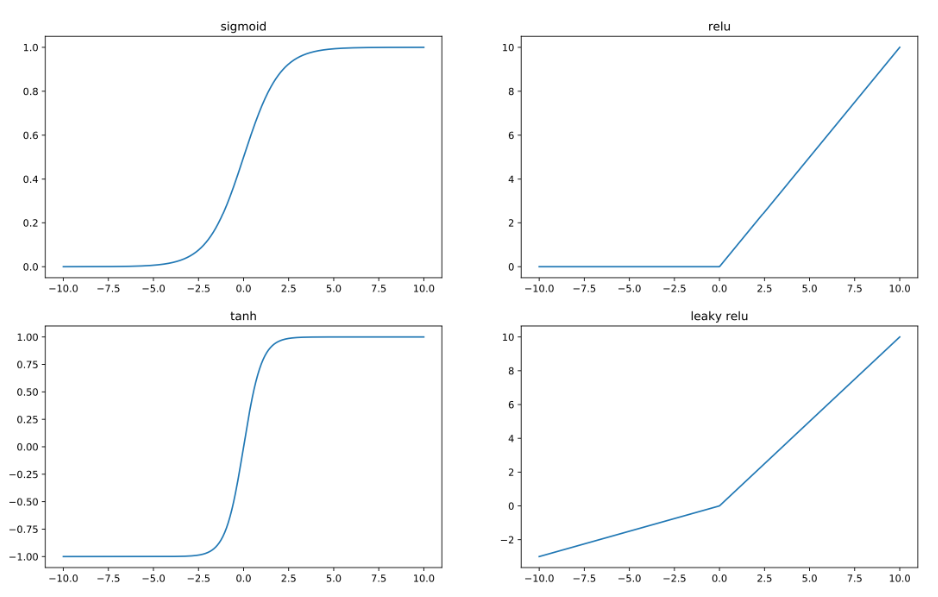
Task1 多头注意力 - 多头乘法

        朴素的矩阵乘法仅对 A1 中 batch_size 维度，针对每个序列索引i，都执行 O1[i] = A1[i] @ W1 计算，从而得到形状为 [b, s, e] 的张量 O1。

        在多头矩阵乘法中，我们首先将输入张量 A1 和权重张量 W1 的 h 维度均分为 num_heads 个子维度（记为 nh，表示头的数量），由此得到形状为 [b, s, nh, hd] 的四维张量 A2 和形状为 [nh, hd, e] 的三维张量 W2。

        接下来，对于 A2 中 batch_size 维度下的每个序列，遍历其 num_heads 维度上的每个 [s, hd] 矩阵，并将其与 W2 中 num_heads 维度下对应的 [hd, e] 矩阵进行乘法运算。通过多头并行计算，最终输出一个形状为 [b, s, nh, e] 的四维张量 O2。

1. 输入输出形状：

• 输入A1: [b, s, h] = [batch_size, seq_len, hidden_size]

• 权重W1: [h, e] = [hidden_size, embed_size]

• 输出O2: [b, s, nh, e] = [batch_size, seq_len, num_heads, embed_size]

2. 计算步骤：

1. 维度分割：

   • 将 h 维度分割为 nh 个头，每个头维度为 hd = h / nh

   • A1 重塑为 [b, s, nh, hd]

   • W1 重塑为 [nh, hd, e]

2. 并行矩阵乘法：

   • 对于每个头 i (0 ≤ i < nh)：

     • 取 A1 的 [:, :, i, :] 形状为 [b, s, hd]

     • 取 W1 的 [i, :, :] 形状为 [hd, e]

     • 计算矩阵乘法：[b, s, hd] @ [hd, e] = [b, s, e]

3. 组合结果：

   • 将所有头的输出堆叠在维度2，得到 [b, s, nh, e]

 

3. 代码实现

Args: input (torch.Tensor):                      # TODO中的输入输出规约

input tensor in the range of [-1, 1], with shape: [batch_size, seq_len, hidden_size]

weight (torch.Tensor): weight tensor in the range of [-1, 1], with shape: [hidden_size, embed_size]

num_heads (int): number of heads to split hidden_size

Returns: output (torch.Tensor): output tensor, with shape: [batch_size, seqlen, num_heads, embed_size]

def matmul_with_multi_head(input: torch.Tensor,weight: torch.Tensor,num_heads: int = 1,
) -> torch.Tensor:# 获取输入形状batch_size, seq_len, hidden_size = input.shapeembed_size = weight.shape[1]# 检查hidden_size是否能被num_heads整除if hidden_size % num_heads != 0:raise ValueError(f"hidden_size ({hidden_size}) must be divisible by num_heads ({num_heads})")# 计算每个头的维度head_dim = hidden_size // num_heads# 重塑输入张量: [b, s, h] -> [b, s, nh, hd]input_reshaped = input.view(batch_size, seq_len, num_heads, head_dim)# 重塑权重张量: [h, e] -> [nh, hd, e]weight_reshaped = weight.view(num_heads, head_dim, embed_size)# 使用einsum进行批量矩阵乘法# b: batch_size, s: seq_len, h: head_index, d: head_dim, e: embed_sizeoutput = torch.einsum('bshd,hde->bshe', input_reshaped, weight_reshaped)return output

Task2 多头注意力 - 只算重要性高的 + 梯度

1. 题目要求

        在多头矩阵乘法的基础上，我们引入一个表示“重要性”的概率张量 P，其形状为 [b, s]。P 中的每个元素表示 A1 中对应位置的元素的重要程度。基于这个重要性概率，我们的目标是只对每个序列中的 “重要” 元素执行矩阵乘法运算。

        （ [b, s] -> t）重要元素总共有t 个，计算结果收集到输出张量 O3 中，形状为 [t, nh, e]。

        如果提供了输出张量的可选梯度（记为 dO3，其形状与 O3 相同），我们还需要计算输入张量的梯度（记为 dA1，形状与 A1 相同）和权重张量的梯度（记为 dW1，形状与 W1 相同）。否则均返回 None。

2. 重要性筛选 [b, s] -> t

weight_reshaped 同Task1 分为多头；

def matmul_with_importance(input: torch.Tensor,weight: torch.Tensor,probs: torch.Tensor,grad_output: Optional[torch.Tensor] = None,num_heads: int = 1,top_p: float = 1.0,top_k: Optional[int] = None,
) -> Tuple[torch.Tensor, Optional[torch.Tensor], Optional[torch.Tensor]]:batch_size, seq_len, hidden_size = input.shapeembed_size = weight.shape[1]# 检查hidden_size是否能被num_heads整除if hidden_size % num_heads != 0:raise ValueError(f"hidden_size ({hidden_size}) must be divisible by num_heads ({num_heads})")head_dim = hidden_size // num_heads# 重塑权重张量: [h, e] -> [nh, hd, e]weight_reshaped = weight.view(num_heads, head_dim, embed_size)

进行矩阵的与&操作，进行重要性高的筛选。

torch.topk 返回前k大的值和对应索引。   

    # 筛选重要的元素mask = torch.ones_like(probs, dtype=torch.bool)# 应用top-p筛选 (保留大于等于top_p的概率)if top_p < 1.0:top_p_mask = probs >= top_pmask = mask & top_p_mask # 矩阵与&一下# 应用top-k筛选if top_k is not None and top_k < seq_len:# 获取每个batch中top_k的概率索引_, topk_indices = torch.topk(probs, top_k, dim=1) # indices 前k的索引topk_mask = torch.zeros_like(probs, dtype=torch.bool)for i in range(batch_size):topk_mask[i, topk_indices[i]] = True # 把前k的索引位置置为Truemask = mask & topk_mask # 矩阵与&一下

特判如果没有重要元素，返回空张量；要返回梯度 就返回0张量。

    # 如果没有重要元素，返回空张量if len(batch_indices) == 0:empty_output = torch.empty(0, num_heads, embed_size,device=input.device, dtype=input.dtype)if grad_output is not None: # Task 3 要返回梯度 都零张量empty_grad_input = torch.zeros_like(input)empty_grad_weight = torch.zeros_like(weight)return empty_output, empty_grad_input, empty_grad_weightelse:return empty_output, None, None

torch.where 返回符合重要性的(b,s) 位置索引。

把索引对应的元素拿出来，拼成 t 个元素。再进行多头乘法。

    # 获取筛选后的二维索引 (b,s) 对应非零位置 batch_indices, seq_indices = torch.where(mask)# 收集筛选后的输入selected_input = input[batch_indices, seq_indices]  # [t, h]# 重塑输入: [t, h] -> [t, nh, hd]selected_input_reshaped = selected_input.view(-1, num_heads, head_dim)# 多头矩阵乘法: [t, nh, hd] @ [nh, hd, e] -> [t, nh, e]output = torch.einsum('tnh,nhd->tnd', selected_input_reshaped, weight_reshaped)# Task2: 如果没有梯度输出，直接返回结果if grad_output is None:return output, None, None

3. 梯度计算

多头乘法算梯度

grad_input_selected = grad_output @ weight_reshaped^T维度：
grad_output:    [t, nh, e]
weight_reshaped^T: [nh, e, hd]  （对最后两个维度转置）
结果：          [t, nh, hd]

    # Task3: 如果有梯度输出，计算梯度# 检查grad_output形状是否正确expected_shape = (len(batch_indices), num_heads, embed_size)if grad_output.shape != expected_shape:raise ValueError(f"grad_output shape {grad_output.shape} doesn't match expected shape {expected_shape}")# 初始化梯度张量grad_input = torch.zeros_like(input)# 1. 计算输入梯度 (grad_input)# 原理: ∂L/∂input = ∂L/∂output * ∂output/∂input = grad_output * weight^T# weight_reshaped: [nh, hd, e] -> 转置为 [nh, e, hd]weight_T = weight_reshaped.transpose(1, 2)  # [nh, e, hd]# 计算筛选位置的梯度: [t, nh, hd] = [t, nh, e] @ [nh, e, hd]grad_input_selected = torch.einsum('tne,neh->tnh', grad_output, weight_T)# 重塑为原始hidden_size维度: [t, nh, hd] -> [t, h]grad_input_selected_flat = grad_input_selected.reshape(-1, hidden_size)# 将梯度放回原始位置（只对筛选出的位置有梯度）grad_input[batch_indices, seq_indices] = grad_input_selected_flat

# 2. 计算权重梯度 (grad_weight)
# 原理: ∂L/∂weight = ∂L/∂output * ∂output/∂weight = input^T * grad_output
# 计算每个头的权重梯度: [nh, hd, e] = [t, nh, hd]^T @ [t, nh, e]

    # 2. 计算权重梯度 (grad_weight)# 原理: ∂L/∂weight = ∂L/∂output * ∂output/∂weight = input^T * grad_output# 计算每个头的权重梯度: [nh, hd, e] = [t, nh, hd]^T @ [t, nh, e]grad_weight_reshaped = torch.einsum('tnh,tne->nhe', selected_input_reshaped, grad_output)# 重塑回原始权重形状: [nh, hd, e] -> [h, e]grad_weight = grad_weight_reshaped.reshape(hidden_size, embed_size)return output, grad_input, grad_weight