育苗盘补苗路径规划研究_2.5

第一个代码

“自动移栽（取苗-放苗）”的模拟过程，包含目标盘（Target Plate）和供苗盘（Source Plate），

并采用 按列固定顺序取苗的算法。

---

代码整体逻辑

1. 参数设定

   • 定义了孔径、行列数、盘子间距、盘子尺寸等基础参数。
   • 每个盘子就是一个带有行、列坐标的孔阵列。

2. 生成盘子函数

   • generate_plate_positions：生成一个盘的所有孔坐标，并标记状态（默认 "Normal"）。
   • initialize_target_plate：生成目标盘，并随机挑选 10~15 个孔设为 "Empty"（需要填充）。
   • initialize_source_plate：生成供苗盘，并随机挑选 10~15 个孔设为 "Empty"（没有苗）。

3. 固定列顺序算法（核心）

   • 一次性初始化 供苗盘。

   • 按照“列优先，列内从下到上”的顺序，生成一个全局的取苗序列。

   • 不断生成新的目标盘：

     • 找到目标盘上所有 "Empty" 的孔（需要填充），排序（按行列）。

     • 对每个空孔：

       1. 从供苗盘取出一个 "Normal" 苗（按列顺序）。
       2. 走到供苗孔 → 再走到目标孔，完成移栽。
       3. 更新状态（供苗孔变 "Taken"，目标孔变 "Filled"）。

     • 每个目标盘填完后，路径回到起点 (0,0)。

   • 重复直到供苗盘没有苗可用。

4. 路径与统计

   • 记录每次移动的路径、累计的移动距离和耗时（简单用 time.time() 模拟）。
   • 统计完成的目标盘数量和剩余苗数。

5. 可视化

   • plot_result：绘制供苗盘和目标盘的孔分布、路径和状态变化。
   • 空孔、填充孔、取走孔都用不同颜色和标记区分。

6. 输出结果

   • 打印总路径距离、总耗时、完成目标盘数量、剩余苗数。

---

代码模拟了一个 移栽机器人 的工作过程：

• 从供苗盘中 按列顺序取苗，
• 将苗移植到目标盘的 空孔，
• 计算并绘制路径，统计总距离、耗时和完成情况。

---

import time
import matplotlib.pyplot as plt
import numpy as np
import random# -------------------------
# Base Parameters
# -------------------------
hole_diameter = 32       # Diameter of each hole
num_cols = 8             # Number of holes per row
num_rows = 16            # Number of rows
plate_spacing = 100      # Spacing between plates
plate_width = num_cols * hole_diameter
plate_height = num_rows * hole_diameter# -------------------------
# Generate Plate Positions
# -------------------------
def generate_plate_positions(x0, y0, rows, cols, plate_name):"""Generate coordinates for the holes on the plate, with x and y values."""positions = []for i in range(rows):for j in range(cols):positions.append({"plate": plate_name,"row": i + 1,"col": j + 1,"x": x0 + j * hole_diameter + hole_diameter / 2,"y": y0 + i * hole_diameter + hole_diameter / 2,"status": "Normal"})return positions# -------------------------
# Initialize Target Plate
# -------------------------
def initialize_target_plate(x0, y0, rows, cols):"""Initialize target plate, randomly fill 10-15 empty positions."""target_plate = generate_plate_positions(x0, y0, rows, cols, "Target Plate")# Randomly generate 10-15 empty holesnum_empty = random.randint(10, 15)empty_holes = sorted(random.sample(target_plate, num_empty), key=lambda k: (k["row"], k["col"]))# Mark these holes as "Empty"for hole in empty_holes:hole["status"] = "Empty"return target_plate, empty_holes# -------------------------
# Initialize Source Plate
# -------------------------
def initialize_source_plate(x0, y0, rows, cols):"""Initialize source plate, randomly fill 10-15 empty positions."""source_plate = generate_plate_positions(x0, y0, rows, cols, "Source Plate")# Randomly generate 10-15 empty holesnum_empty = random.randint(10, 15)empty_holes = sorted(random.sample(source_plate, num_empty), key=lambda k: (k["row"], k["col"]))# Mark these holes as "Empty"for hole in empty_holes:hole["status"] = "Empty"return source_plate, empty_holes# -------------------------
# Fixed Order Algorithm
# -------------------------
def fixed_order_algorithm():total_distance = 0total_time = 0completed_plates = 0last_plate_incomplete = 0current_pos = np.array([0, 0])# 初始化供苗盘（只生成一次）source_plate, empty_holes_source = initialize_source_plate(30 + plate_width + plate_spacing, 30, num_rows, num_cols)while True:# 每次循环只重新生成目标盘target_plate, empty_holes_target = initialize_target_plate(30, 30, num_rows, num_cols)empty_indices_target = [(h["row"], h["col"]) for h in empty_holes_target]fixed_empty_holes = []for hole in target_plate:if (hole["row"], hole["col"]) in empty_indices_target:hole["status"] = "Empty"fixed_empty_holes.append(hole)# 按行列排序fixed_empty_holes.sort(key=lambda h: (h["row"], h["col"]))# 供苗盘可用苗（Normal 才能取，Empty 和 Taken 不能用）seedlings_by_row = {r: [] for r in range(1, num_rows + 1)}for s in source_plate:if s["status"] == "Normal":seedlings_by_row[s["row"]].append(s)for r in seedlings_by_row:seedlings_by_row[r].sort(key=lambda s: s["col"])path = [(0, 0)]start_time = time.time()# 填充目标盘for hole in fixed_empty_holes:row = hole["row"]if seedlings_by_row[row]:seedling = seedlings_by_row[row].pop(0)else:last_plate_incomplete = rowbreak# current -> seedlingpath.append((seedling["x"], seedling["y"]))total_distance += np.linalg.norm(current_pos - np.array([seedling["x"], seedling["y"]]))seedling["status"] = "Taken"# seedling -> holepath.append((hole["x"], hole["y"]))total_distance += np.linalg.norm(np.array([seedling["x"], seedling["y"]]) - np.array([hole["x"], hole["y"]]))hole["status"] = "Filled"current_pos = np.array([hole["x"], hole["y"]])# 回到起点path.append((0, 0))total_distance += np.linalg.norm(current_pos - np.array([0, 0]))end_time = time.time()total_time += end_time - start_timecompleted_plates += 1plot_result(path,target_plate,source_plate,f"Fixed Order Algorithm (Distance={total_distance:.2f}, Time={total_time:.10f}s)")if last_plate_incomplete > 0:breakremaining_seedlings = sum([1 for s in source_plate if s["status"] == "Normal"])return path, total_distance, total_time, completed_plates, last_plate_incomplete, remaining_seedlings, target_plate, source_plate# -------------------------
# Plotting Function
# -------------------------
def plot_result(path, target_plate, source_plate, title):"""Plot the allocation of target and source plates, display the path and status."""fig, ax = plt.subplots(figsize=(12, 8))ax.set_aspect('equal')# Plot target platefor hole in target_plate:if hole["status"] == "Empty":ax.text(hole["x"], hole["y"], "X", color="blue", fontsize=12, ha="center", va="center")elif hole["status"] == "Filled":ax.scatter(hole["x"], hole["y"], s=80, c="red", marker="o")else:ax.scatter(hole["x"], hole["y"], s=40, facecolors='none', edgecolors='blue')# Plot source platefor hole in source_plate:if hole["status"] == "Taken":ax.text(hole["x"], hole["y"], "X", color="red", fontsize=12, ha="center", va="center")elif hole["status"] == "Empty":ax.scatter(hole["x"], hole["y"], s=150, c="red", marker="o")  # 初始空位 -> 大红点else:ax.scatter(hole["x"], hole["y"], s=40, facecolors='none', edgecolors='red')# Plot pathfor i in range(len(path) - 1):ax.annotate('', xy=path[i + 1], xytext=path[i],arrowprops=dict(arrowstyle="->", color='green', lw=1.5))# Start point markerax.scatter(0, 0, s=100, c="black", marker="*", label="Start (0,0)")# Set plot parametersax.set_xlim(-50, plate_width * 2 + plate_spacing + 100)ax.set_ylim(-50, plate_height + 100)ax.set_xlabel("X / mm")ax.set_ylabel("Y / mm")ax.set_title(title)ax.legend()plt.tight_layout()plt.show()# -------------------------
# Main Program
# -------------------------
path_fixed, dist_fixed, time_fixed, completed_plates, last_plate_incomplete, remaining_seedlings, tp_fixed, sp_fixed = fixed_order_algorithm()# Output results
print("Total Path Distance =", dist_fixed)
print("Total Time =", time_fixed)
print("Completed Plates =", completed_plates)
print("Last Incomplete Row =", last_plate_incomplete)
print("Remaining Seedlings =", remaining_seedlings)

第二个代码

对比两种移栽算法：固定列顺序算法 vs 贪心算法。

---

代码逻辑摘要

1. 基础参数

• 定义孔径、行数、列数、盘子间距和盘子大小。
• 一个“盘”就是带有行列坐标的孔阵列，每个孔有状态（Normal / Empty / Taken / Filled）。

---

2. 盘子生成与初始化

• generate_plate_positions()：生成某个盘所有孔的坐标和状态（默认 "Normal"）。
• initialize_plate()：初始化盘子，随机挑出 10~15 个空孔，标记为 "Empty"；也可以传入固定的空孔索引。

---

3. 固定列顺序算法 (fixed_order_algorithm)

• 生成供苗盘的 全局顺序：按列，从下到上。

• 循环生成目标盘：

  1. 找出所有空孔，按行列排序。
  2. 按照全局顺序依次取苗，填充目标盘的空孔。
  3. 路径计算：当前点 → 取苗孔 → 移栽孔 → 更新状态。
  4. 每个目标盘完成后回到 (0,0)。

• 统计总路径长度、耗时、完成的目标盘数量。

---

4. 贪心算法 (greedy_algorithm)

• 在每一步：

  1. 找到 离当前位置最近的苗。
  2. 从该苗出发，找 离它最近的空孔。
  3. 移栽并更新状态。

• 不断重复，直到所有苗或空孔用完。

• 同样统计总路径长度、耗时、完成的目标盘数量。

---

5. 绘图函数

• plot_result()：画出供苗盘、目标盘和路径：

  • 不同状态的孔用不同颜色/标记表示。
  • 箭头显示路径。
  • 起点 (0,0) 用黑色星号标记。

---

6. 主程序对比 (run_comparison())

1. 初始化相同的供苗盘和目标盘空孔（保证公平比较）。

2. 拷贝数据，分别交给 固定列顺序算法 和 贪心算法。

3. 输出对比结果：

   • 总路径距离
   • 总耗时
   • 完成的目标盘数

---

这段代码模拟了一个移栽机器人，用 两种策略把供苗盘的苗移植到目标盘的空孔里：

• 固定列顺序：按列逐个搬运，规则简单。
• 贪心算法：每次选择最近的苗和最近的孔，路径更短。

最后通过绘图和数据统计对比两种算法的效率（距离、时间、完成盘数）。

---

import time
import matplotlib.pyplot as plt
import numpy as np
import random
import copy# -------------------------
# Base Parameters
# -------------------------
hole_diameter = 32
num_cols = 8
num_rows = 16
plate_spacing = 100
plate_width = num_cols * hole_diameter
plate_height = num_rows * hole_diameter# -------------------------
# Generate Plate Positions
# -------------------------
def generate_plate_positions(x0, y0, rows, cols, plate_name):positions = []for i in range(rows):for j in range(cols):positions.append({"plate": plate_name,"row": i + 1,"col": j + 1,"x": x0 + j * hole_diameter + hole_diameter / 2,"y": y0 + i * hole_diameter + hole_diameter / 2,"status": "Normal"})return positions# -------------------------
# Initialize Plate with Fixed Empty Holes
# -------------------------
def initialize_plate(x0, y0, rows, cols, plate_name, empty_indices=None):plate = generate_plate_positions(x0, y0, rows, cols, plate_name)if empty_indices is None:num_empty = random.randint(10, 15)empty_holes = random.sample(range(len(plate)), num_empty)else:empty_holes = empty_indicesfor idx in empty_holes:plate[idx]["status"] = "Empty"return plate, empty_holes# -------------------------
# Fixed Column-Order Algorithm (Multi Plates)
# -------------------------
def fixed_order_algorithm(source_plate, empty_indices_target):total_distance = 0total_time = 0completed_plates = 0current_pos = np.array([0, 0])path = []# 全局顺序：按列，从下到上column_order = []for c in range(1, num_cols + 1):col_seeds = [s for s in source_plate if s["col"] == c and s["status"] == "Normal"]col_seeds.sort(key=lambda s: s["row"])column_order.extend(col_seeds)seed_index = 0while seed_index < len(column_order):target_plate, _ = initialize_plate(30, 30, num_rows, num_cols, "Target Plate", empty_indices_target)fixed_empty_holes = [h for h in target_plate if h["status"] == "Empty"]fixed_empty_holes.sort(key=lambda h: (h["row"], h["col"]))local_path = [(0, 0)]start_time = time.time()for hole in fixed_empty_holes:if seed_index >= len(column_order):breakseedling = column_order[seed_index]while seed_index < len(column_order) and seedling["status"] != "Normal":seed_index += 1if seed_index < len(column_order):seedling = column_order[seed_index]if seed_index >= len(column_order):break# current -> seedlinglocal_path.append((seedling["x"], seedling["y"]))total_distance += np.linalg.norm(current_pos - np.array([seedling["x"], seedling["y"]]))seedling["status"] = "Taken"# seedling -> holelocal_path.append((hole["x"], hole["y"]))total_distance += np.linalg.norm(np.array([seedling["x"], seedling["y"]]) - np.array([hole["x"], hole["y"]]))hole["status"] = "Filled"current_pos = np.array([hole["x"], hole["y"]])seed_index += 1# 回到起点local_path.append((0, 0))total_distance += np.linalg.norm(current_pos - np.array([0, 0]))end_time = time.time()total_time += end_time - start_timecompleted_plates += 1path.append(local_path)# 绘制每个目标盘结果plot_result(local_path, target_plate, source_plate,f"Fixed Order Plate {completed_plates} (Dist={total_distance:.2f}, Time={total_time:.5f}s)")return path, total_distance, total_time, completed_plates# -------------------------
# Greedy Algorithm (Multi Plates)
# -------------------------
def greedy_algorithm(source_plate, empty_indices_target):total_distance = 0total_time = 0completed_plates = 0current_pos = np.array([0, 0])path = []available_seedlings = [s for s in source_plate if s["status"] == "Normal"]while available_seedlings:target_plate, _ = initialize_plate(30, 30, num_rows, num_cols, "Target Plate", empty_indices_target)available_holes = [h for h in target_plate if h["status"] == "Empty"]local_path = [(0, 0)]start_time = time.time()while available_seedlings and available_holes:# 找到最近的苗nearest_seedling = min(available_seedlings,key=lambda s: np.linalg.norm(current_pos - np.array([s["x"], s["y"]])))local_path.append((nearest_seedling["x"], nearest_seedling["y"]))total_distance += np.linalg.norm(current_pos - np.array([nearest_seedling["x"], nearest_seedling["y"]]))# 找最近的空穴nearest_hole = min(available_holes,key=lambda h: np.linalg.norm(np.array([nearest_seedling["x"], nearest_seedling["y"]]) - np.array([h["x"], h["y"]])))local_path.append((nearest_hole["x"], nearest_hole["y"]))total_distance += np.linalg.norm(np.array([nearest_seedling["x"], nearest_seedling["y"]]) - np.array([nearest_hole["x"], nearest_hole["y"]]))nearest_seedling["status"] = "Taken"nearest_hole["status"] = "Filled"current_pos = np.array([nearest_hole["x"], nearest_hole["y"]])available_seedlings = [s for s in source_plate if s["status"] == "Normal"]available_holes = [h for h in target_plate if h["status"] == "Empty"]# 回到起点local_path.append((0, 0))total_distance += np.linalg.norm(current_pos - np.array([0, 0]))end_time = time.time()total_time += end_time - start_timecompleted_plates += 1path.append(local_path)plot_result(local_path, target_plate, source_plate,f"Greedy Plate {completed_plates} (Dist={total_distance:.2f}, Time={total_time:.5f}s)")return path, total_distance, total_time, completed_plates# -------------------------
# Plotting Function
# -------------------------
def plot_result(path, target_plate, source_plate, title):fig, ax = plt.subplots(figsize=(12, 8))ax.set_aspect('equal')# Target platefor hole in target_plate:if hole["status"] == "Empty":ax.text(hole["x"], hole["y"], "X", color="blue", fontsize=12, ha="center", va="center")elif hole["status"] == "Filled":ax.scatter(hole["x"], hole["y"], s=80, c="red", marker="o")else:ax.scatter(hole["x"], hole["y"], s=40, facecolors='none', edgecolors='blue')# Source platefor hole in source_plate:if hole["status"] == "Taken":ax.text(hole["x"], hole["y"], "X", color="red", fontsize=12, ha="center", va="center")elif hole["status"] == "Empty":ax.scatter(hole["x"], hole["y"], s=150, c="red", marker="o")else:ax.scatter(hole["x"], hole["y"], s=40, facecolors='none', edgecolors='red')# Pathfor i in range(len(path) - 1):ax.annotate('', xy=path[i + 1], xytext=path[i],arrowprops=dict(arrowstyle="->", color='green', lw=1.5))ax.scatter(0, 0, s=100, c="black", marker="*", label="Start (0,0)")ax.set_xlim(-50, plate_width * 2 + plate_spacing + 100)ax.set_ylim(-50, plate_height + 100)ax.set_xlabel("X / mm")ax.set_ylabel("Y / mm")ax.set_title(title)ax.legend()plt.tight_layout()plt.show()# -------------------------
# Main Program
# -------------------------
def run_comparison():# 生成相同的随机空位source_plate, empty_indices_source = initialize_plate(30 + plate_width + plate_spacing, 30, num_rows, num_cols, "Source Plate")_, empty_indices_target = initialize_plate(30, 30, num_rows, num_cols, "Target Plate")# 深拷贝，保证两个算法用相同数据source_plate_fixed = copy.deepcopy(source_plate)source_plate_greedy = copy.deepcopy(source_plate)# 固定列序算法_, dist_fixed, time_fixed, completed_fixed = fixed_order_algorithm(source_plate_fixed, empty_indices_target)# 贪心算法_, dist_greedy, time_greedy, completed_greedy = greedy_algorithm(source_plate_greedy, empty_indices_target)print("=== Result Comparison ===")print(f"Fixed Order -> Distance: {dist_fixed:.2f}, Time: {time_fixed:.5f}s, Plates: {completed_fixed}")print(f"Greedy      -> Distance: {dist_greedy:.2f}, Time: {time_greedy:.5f}s, Plates: {completed_greedy}")if __name__ == "__main__":run_comparison()

对比

移栽路径规划对比实验，比较 固定列序算法 和 贪心算法

核心内容摘要：

1. 实验背景

   • 模拟苗盘（Source Plate）和目标盘（Target Plate），每个盘有固定的孔洞阵列。
   • 孔洞里有的空、有的正常，有苗的孔需要被移到目标盘的空孔中。

2. 算法设计

   • 固定列序算法（Fixed Order）：按固定顺序（逐列，从下到上）依次取苗并填充目标盘空位。
   • 贪心算法（Greedy）：每次选择距离当前位置最近的苗孔，再将其放到距离最近的目标空孔。

3. 指标统计

   • 累计路径长度（total distance）：机器人臂在取苗、移苗、回归起点过程中的移动距离总和。
   • 完成目标盘数量与对应的累计路径长度。

4. 实验流程

   • 多次随机生成供苗盘和目标盘（含随机空孔位置）。
   • 运行两种算法，记录每完成一个目标盘后的累计路径长度。
   • 汇总 20 次实验结果，计算均值和标准差。

5. 结果输出

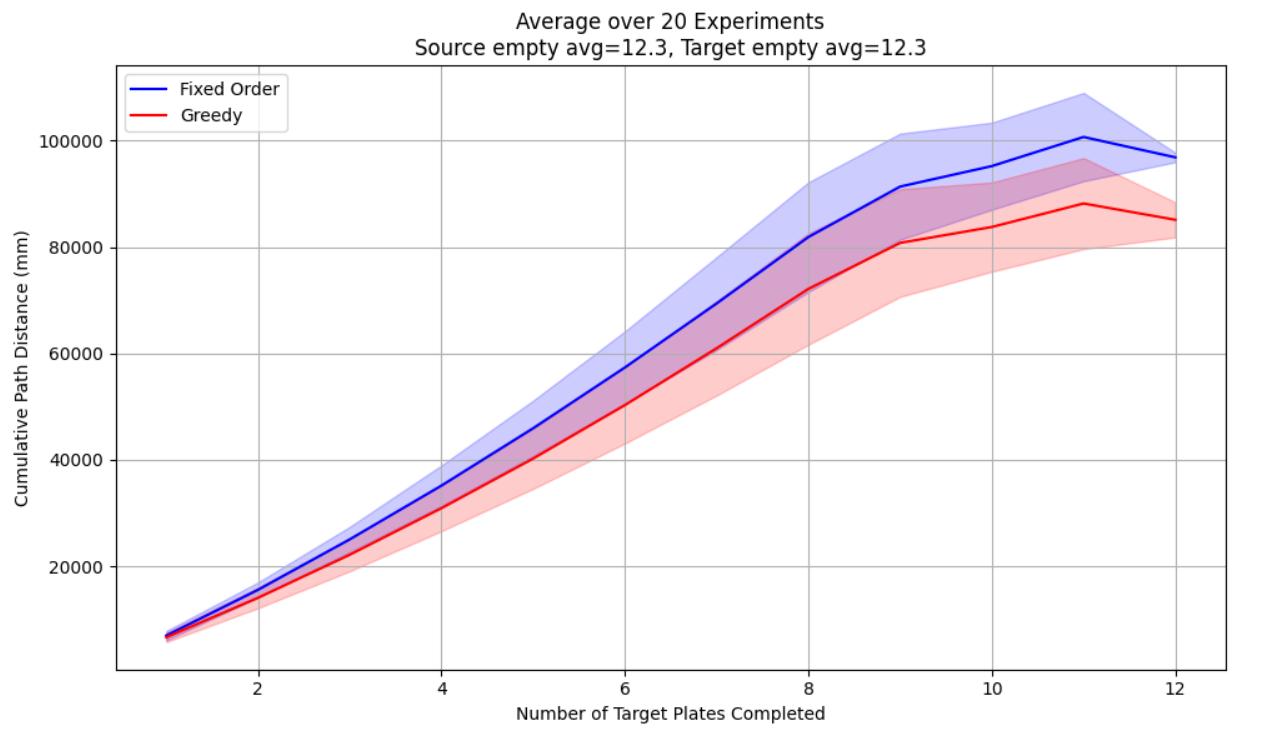
   • 绘制折线图，横轴为“完成的目标盘数”，纵轴为“累计路径长度”。
   • 曲线包含 均值 ± 标准差，便于比较两种算法的稳定性与效率。
   • 标题中还显示了源盘和目标盘的平均空孔数。

👉 总体来说，这个程序用于验证 固定顺序搬运 vs 贪心搬运 的效率差异，并可视化对比实验结果。

import time
import matplotlib.pyplot as plt
import numpy as np
import random
import copy# -------------------------
# Base Parameters
# -------------------------
hole_diameter = 32
num_cols = 8
num_rows = 16
plate_spacing = 100
plate_width = num_cols * hole_diameter
plate_height = num_rows * hole_diameter# -------------------------
# Generate Plate Positions
# -------------------------
def generate_plate_positions(x0, y0, rows, cols, plate_name):positions = []for i in range(rows):for j in range(cols):positions.append({"plate": plate_name,"row": i + 1,"col": j + 1,"x": x0 + j * hole_diameter + hole_diameter / 2,"y": y0 + i * hole_diameter + hole_diameter / 2,"status": "Normal"})return positions# -------------------------
# Initialize Plate
# -------------------------
def initialize_plate(x0, y0, rows, cols, plate_name, empty_indices=None):plate = generate_plate_positions(x0, y0, rows, cols, plate_name)if empty_indices is None:num_empty = random.randint(10, 15)empty_holes = random.sample(range(len(plate)), num_empty)else:empty_holes = empty_indicesfor idx in empty_holes:plate[idx]["status"] = "Empty"return plate, empty_holes# -------------------------
# Fixed Column-Order Algorithm (Multi Plates)
# -------------------------
def fixed_order_algorithm(source_plate, empty_indices_target):total_distance = 0completed_plates = 0current_pos = np.array([0, 0])dist_progress = []# 全局顺序：按列，从下到上column_order = []for c in range(1, num_cols + 1):col_seeds = [s for s in source_plate if s["col"] == c and s["status"] == "Normal"]col_seeds.sort(key=lambda s: s["row"])column_order.extend(col_seeds)seed_index = 0while seed_index < len(column_order):target_plate, _ = initialize_plate(30, 30, num_rows, num_cols, "Target Plate", empty_indices_target)fixed_empty_holes = [h for h in target_plate if h["status"] == "Empty"]fixed_empty_holes.sort(key=lambda h: (h["row"], h["col"]))for hole in fixed_empty_holes:if seed_index >= len(column_order):breakseedling = column_order[seed_index]while seed_index < len(column_order) and seedling["status"] != "Normal":seed_index += 1if seed_index < len(column_order):seedling = column_order[seed_index]if seed_index >= len(column_order):break# 移动 current -> seedlingtotal_distance += np.linalg.norm(current_pos - np.array([seedling["x"], seedling["y"]]))seedling["status"] = "Taken"# 移动 seedling -> holetotal_distance += np.linalg.norm(np.array([seedling["x"], seedling["y"]]) - np.array([hole["x"], hole["y"]]))hole["status"] = "Filled"current_pos = np.array([hole["x"], hole["y"]])seed_index += 1# 回到起点total_distance += np.linalg.norm(current_pos - np.array([0, 0]))current_pos = np.array([0, 0])completed_plates += 1dist_progress.append(total_distance)return dist_progress# -------------------------
# Greedy Algorithm (Multi Plates)
# -------------------------
def greedy_algorithm(source_plate, empty_indices_target):total_distance = 0completed_plates = 0current_pos = np.array([0, 0])dist_progress = []available_seedlings = [s for s in source_plate if s["status"] == "Normal"]while available_seedlings:target_plate, _ = initialize_plate(30, 30, num_rows, num_cols, "Target Plate", empty_indices_target)available_holes = [h for h in target_plate if h["status"] == "Empty"]while available_seedlings and available_holes:nearest_seedling = min(available_seedlings,key=lambda s: np.linalg.norm(current_pos - np.array([s["x"], s["y"]])))total_distance += np.linalg.norm(current_pos - np.array([nearest_seedling["x"], nearest_seedling["y"]]))nearest_hole = min(available_holes,key=lambda h: np.linalg.norm(np.array([nearest_seedling["x"], nearest_seedling["y"]]) - np.array([h["x"], h["y"]])))total_distance += np.linalg.norm(np.array([nearest_seedling["x"], nearest_seedling["y"]]) - np.array([nearest_hole["x"], nearest_hole["y"]]))nearest_seedling["status"] = "Taken"nearest_hole["status"] = "Filled"current_pos = np.array([nearest_hole["x"], nearest_hole["y"]])available_seedlings = [s for s in source_plate if s["status"] == "Normal"]available_holes = [h for h in target_plate if h["status"] == "Empty"]# 回到起点total_distance += np.linalg.norm(current_pos - np.array([0, 0]))current_pos = np.array([0, 0])completed_plates += 1dist_progress.append(total_distance)return dist_progress# -------------------------
# Single Experiment
# -------------------------
def run_single_experiment():# 生成供苗盘 & 目标盘空位source_plate, empty_indices_source = initialize_plate(30 + plate_width + plate_spacing, 30, num_rows, num_cols, "Source Plate")_, empty_indices_target = initialize_plate(30, 30, num_rows, num_cols, "Target Plate")# 记录空位数量source_empty_count = len(empty_indices_source)target_empty_count = len(empty_indices_target)# 固定列序fixed_progress = fixed_order_algorithm(copy.deepcopy(source_plate), empty_indices_target)# 贪心greedy_progress = greedy_algorithm(copy.deepcopy(source_plate), empty_indices_target)return fixed_progress, greedy_progress, source_empty_count, target_empty_count# -------------------------
# Multiple Experiments with Averaging
# -------------------------
def run_multiple_experiments(n=20):all_fixed = []all_greedy = []source_empty_counts = []target_empty_counts = []for _ in range(n):fixed_prog, greedy_prog, src_empty, tgt_empty = run_single_experiment()all_fixed.append(fixed_prog)all_greedy.append(greedy_prog)source_empty_counts.append(src_empty)target_empty_counts.append(tgt_empty)# 对齐长度max_len = max(max(len(f) for f in all_fixed), max(len(g) for g in all_greedy))fixed_array = np.full((n, max_len), np.nan)greedy_array = np.full((n, max_len), np.nan)for i in range(n):fixed_array[i, :len(all_fixed[i])] = all_fixed[i]greedy_array[i, :len(all_greedy[i])] = all_greedy[i]# 均值和标准差fixed_mean = np.nanmean(fixed_array, axis=0)fixed_std = np.nanstd(fixed_array, axis=0)greedy_mean = np.nanmean(greedy_array, axis=0)greedy_std = np.nanstd(greedy_array, axis=0)# 绘制均值 ± 标准差曲线plt.figure(figsize=(10,6))x = np.arange(1, max_len+1)plt.plot(x, fixed_mean, label="Fixed Order", color="blue")plt.fill_between(x, fixed_mean-fixed_std, fixed_mean+fixed_std, color="blue", alpha=0.2)plt.plot(x, greedy_mean, label="Greedy", color="red")plt.fill_between(x, greedy_mean-greedy_std, greedy_mean+greedy_std, color="red", alpha=0.2)plt.xlabel("Number of Target Plates Completed")plt.ylabel("Cumulative Path Distance (mm)")plt.title(f"Average over {n} Experiments\n"f"Source empty avg={np.mean(source_empty_counts):.1f}, "f"Target empty avg={np.mean(target_empty_counts):.1f}")plt.legend()plt.grid(True)plt.tight_layout()plt.show()# -------------------------
# Run
# -------------------------
if __name__ == "__main__":run_multiple_experiments(n=20) 

贪心算法相较于固定列顺序算法的优点

路径更短

固定列顺序可能会“绕远路”，因为它严格按列走。

贪心会优先选择最近的苗孔/目标孔，减少不必要的移动。

效率更高

因为路径缩短，累计距离和时间消耗更小。

更贴近实际自动化机械臂/机器人需要的“节能”操作。

自适应性强

固定顺序不考虑孔的实际分布（比如供苗孔正好在目标孔旁边，仍要等到顺序轮到）。

贪心可以动态调整，随时根据当前坐标选择最优。

利用资源更均衡

固定顺序可能导致某些供苗盘区域很快被取空，导致后续操作都要跨大范围移动。

贪心倾向于“就近取苗”，自然会让供苗区域消耗得更均匀。

未来算法比较

算法	核心思路	优点	缺点	适用场景
固定列顺序	按列优先、列内自下而上依次取苗、填孔	简单、可预测、实现容易	路径可能很长、效率低、不能适应随机空孔	规则化实验、对效率要求不高的情况
贪心 (Greedy)	每次选择最近的供苗孔，再选择最近的目标孔	路径更短，效率比固定顺序高，自适应性强	只考虑局部最优，可能导致整体路径不优	动态目标盘、需要一定效率的情况
批量规划 (TSP简化版)	一次选定多个目标孔，按近似最短路径顺序完成	路径更顺滑，减少来回跑，全局效率高	算法复杂度高，需批次划分逻辑	任务量大、对效率要求极高的自动化
启发式贪心 (A*思路)	选择时考虑“当前位置→苗孔+苗孔→目标孔+未来代价”	兼顾当前与未来，避免局部最优，实时性好	启发函数需要设计，仍非绝对最优	动态任务、需要平衡效率与计算成本

加模拟退火算法

启发式贪心 + 模拟退火（SA）就是 实时性 + 全局优化 的组合，可以写成这样：

---

混合算法框架

1. 启发式贪心阶段

   • 根据当前位置、苗孔 → 目标孔距离 + 启发式“未来代价”
   • 快速生成一条“可行路径”
   • 保证实时性（系统马上能用）

2. 模拟退火阶段

   • 以启发式贪心的结果作为初始解
   • 在后台运行，尝试局部交换路径（比如调整访问顺序）
   • 温度逐渐下降，少量接受“更差解”，避免局部最优
   • 得到更短的路径

3. 动态更新

   • 如果 SA 找到更优解 → 更新给执行系统
   • 如果来不及优化 → 继续用原来的启发式贪心路径，保证不会卡住

---

对比指标

我们可以比较三方面：

1. 路径长度

   • 固定列顺序（基线，最差）
   • 贪心（改进）
   • 启发式贪心（更好）
   • 启发式贪心 + 模拟退火（最优或接近最优）

2. 算法运行时间

   • 固定列顺序：O(n)，非常快
   • 贪心：O(n²) 左右（找最近点）
   • 启发式贪心：O(n²)，但比单纯贪心更聪明
   • 启发式贪心 + SA：O(n²) + O(iter × swap)，取决于迭代次数

3. 实时性 vs 全局性

   • 启发式贪心：实时可用
   • SA：慢，但后台可优化
   • 混合策略：前台保证可执行，后台逐步改进

---

启发式贪心 + 模拟退火：

• 优点：路径最短（接近全局最优），实时性好
• 缺点：计算时间更长（但后台可容忍）
• 创新点：把实时启发式和全局优化结合，兼顾速度与质量，非常适合论文/项目展示

---

启发式贪心算法 和 启发式贪心 + 模拟退火 的原理和公式

---

---

# 1. 启发式贪心 (Heuristic Greedy)

原理

• 普通贪心只看 当前位置 → 候选点的距离，容易陷入局部最优。

• 启发式贪心引入“未来代价”估计，即：

  不仅考虑当前位置到候选点的距离，还考虑候选点继续走向其他未访问点的潜在开销。实际是一种全局算法

---

公式推导

设：

• 当前点：$c$
• 候选点集（未访问）：U={q1,q2,…,qm}U = \{q_1, q_2, \dots, q_m\}U={q1​,q2​,…,qm​}
• 距离函数：

$$d(p,q)=\sqrt{(x_p-x_q{)}^2+(y_p-y_q{)}^2}$$

启发式代价函数：

h(c,q)=d(c,q)+min⁡r∈U∖{q}d(q,r)h(c, q) = d(c, q) + \min_{r \in U \setminus \{q\}} d(q, r) h(c,q)=d(c,q)+r∈U∖{q}min​d(q,r)

解释：

• $d(c,q)$：当前位置到候选点的即时开销
• min⁡r∈U∖{q}d(q,r)\min_{r \in U \setminus \{q\}} d(q, r)minr∈U∖{q}​d(q,r)：候选点到未来最近点的估计开销

选择规则：

$$q^{\ast }=\arg \underset{q\in U}{\min }h(c,q)$$

总代价（路径长度）：

$$L_{\text{heur}}=\sum _{i=0}^{|\pi |-2}d({\pi }_i,{\pi }_{i+1})$$

其中 $\pi =[p_0,q_1,q_2,\dots ,q_m,p_0]$ 表示完整路径。

---

# 2. 启发式贪心 + 模拟退火 (Heuristic Greedy + SA)

原理

• 启发式贪心生成一条“较优”的初始解 ${\pi }_0$。
• 模拟退火 (SA) 在邻域中搜索，通过“有概率接受坏解”的机制跳出局部最优，逐步接近全局最优。

---

公式推导

1. 初始解

$${\pi }_0=\text{HeuristicGreedy}(p_0,U)$$

2. 邻域生成
   随机交换路径中两个位置 $i,j$，得到新路径 ${\pi }^{\prime }$。

3. 代价差

$$\Delta E=L({\pi }^{\prime })-L(\pi )$$

4. 接受概率

$$P(\pi \to {\pi }^{\prime })=\{\begin{array}{ll}1,& \Delta E\le 0\\ \exp \left(-\frac{\Delta E}{T}\right),& \Delta E>0\end{array}$$

5. 温度更新

$$T_{k+1}=\alpha \cdot T_k(0<\alpha <1)$$

6. 终止条件
   当温度 $T<T_{\min }$ 或迭代次数达到上限时停止，输出当前最优解 ${\pi }^{\ast }$。

---

总代价

$$L_{\text{SA}}=\sum _{i=0}^{|{\pi }^{\ast }|-2}d({\pi }_i^{\ast },{\pi }_{i+1}^{\ast })$$

---

# 总结对比

算法	选择公式	特点
启发式贪心	q∗=arg⁡min⁡q∈U{d(c,q)+min⁡rd(q,r)}q^* = \arg\min_{q \in U} \{ d(c,q) + \min_{r} d(q,r) \}q∗=argminq∈U​{d(c,q)+minr​d(q,r)}	快速、实时性好，优于单纯贪心
启发式贪心 + SA	以启发式贪心路径为初始解，用 SA 改进	路径最优或接近全局最优，代价是计算时间增加

---

代码见代码仓库