MATLAB7-数值微积分-台大郭彦甫
目录
多项式的积分和微分
多项式的微分
polyval
polyder 求解导数
exercise
多项式的积分
polyint
数值的积分和微分
数值微分
diff()
exercise
如何找0 2*pi区间的f'呢?
various step size
二次微分和三次微分
数值积分
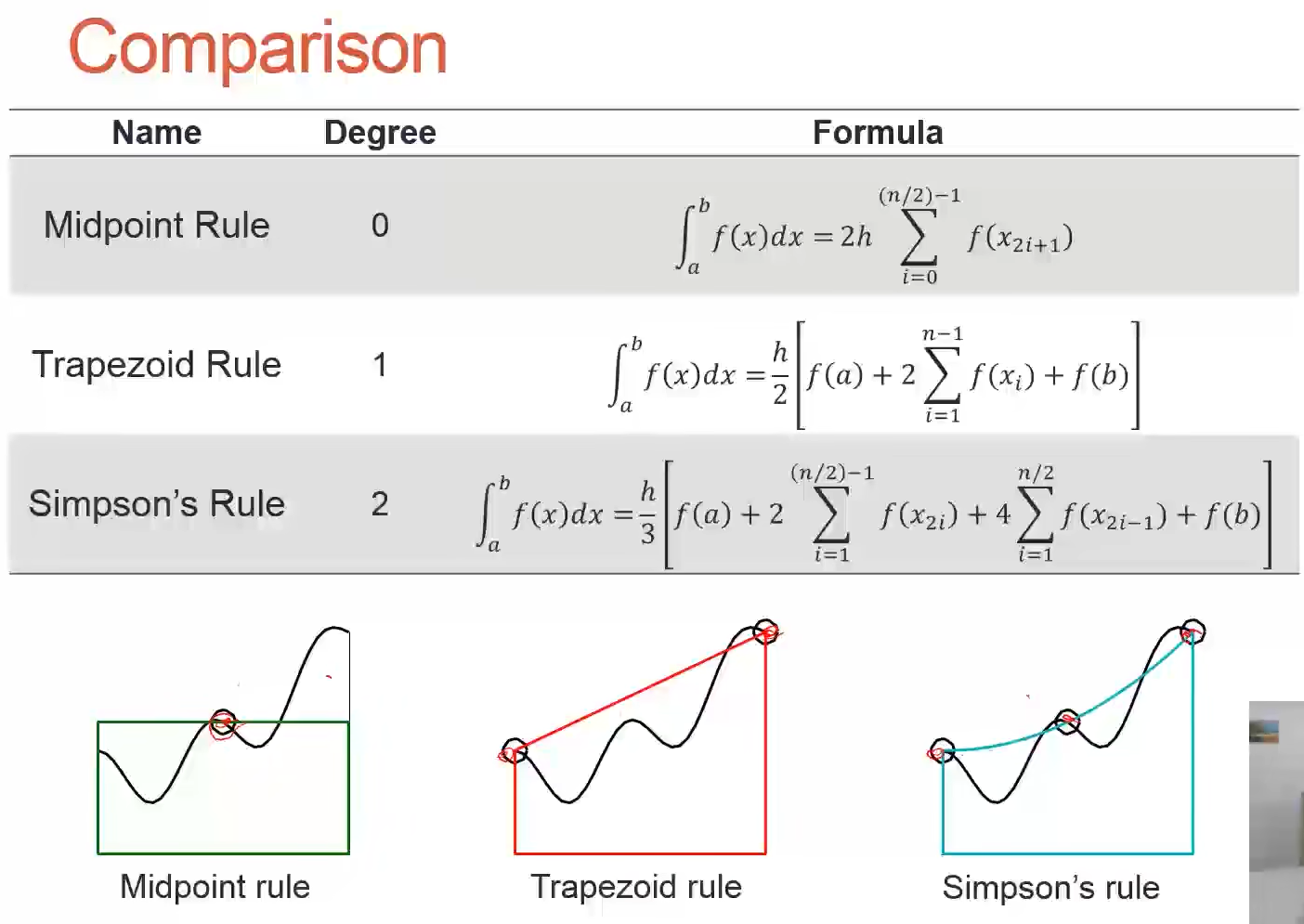
Midpoint Rule中点法则
Trapezoid Rule梯形法则
辛普森公式simpson’s Rule
comparison
匿名函数传递
integral
双重积分double和三重积分integrals
多项式的积分和微分
多项式的微分
就是切线的斜率
polyval
计算多项式的结果
例如求解:f = x^3-2x-5
代码:
%多项式的微分
%多项式的表示f = x^3-2x-5;
%p = [1 0 -2 -5];%f = 9x^3-5x^2+3x+7
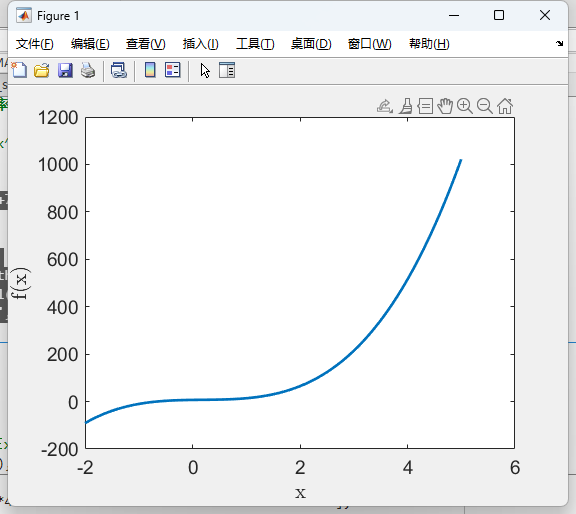
p = [9 -5 3 7];
x = -2:0.1:5;
f = polyval(p,x);
plot(x,f,'LineWidth',2);%绘制多项式曲线,线宽为2
xlabel('x');ylabel('f(x)');
set(gca,'FontSize',14);%设置坐标轴刻度和标签字体大小为14结果:
polyder 求解导数
f = 5x^4-2x^2+1的导数f‘显然是f’=20x^3-4x
代码:
%% polyder
%f = 5x^4-2x^2+1
p = [5 0 -2 0 1];
polyder(p)结果: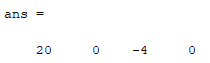
如果想知道f(7)'呢?
polyval(polyder(p),7)
exercise
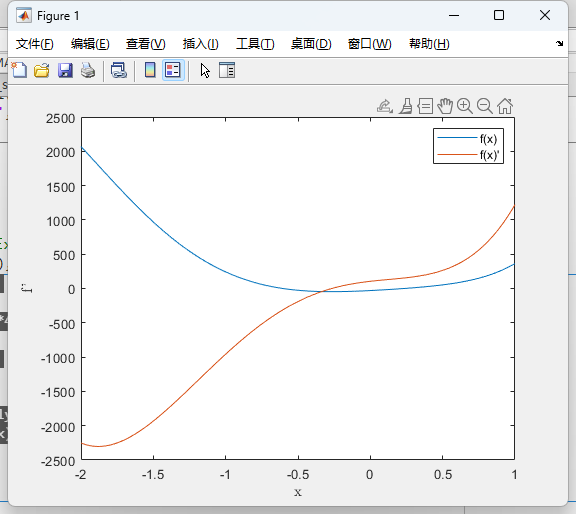
代码:
p = [20*4 20*12-7*4 -20*3-7*12+5*4 4*10+7*3+12*5 120-15 -30];
x = -2:0.01:1;
f = polyval(p,x);
plot(x,f);
hold on;
plot(x,polyval(polyder(p),x));
legend('f(x)','f(x)''');
xlabel('x');
ylabel('f(x)&f(x)''');结果:
多项式的积分
polyint

代码:
x = [1 2 5 2 1];
diff(x);
%(1,5)和(2,7)的斜率
x = [1 2];y = [5 7];
slope = diff(y)./diff(x);
x0 = 0.5*pi;h = 0.01;
x = [x0 x0+h];
y = [sin(x0) sin(x0+h)];
m = diff(y)./diff(x)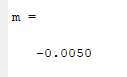
数值的积分和微分
数值微分
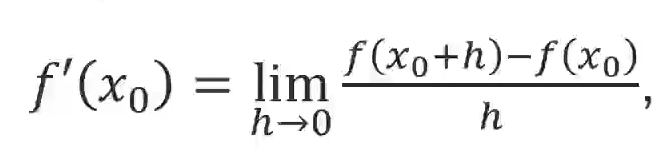
diff()
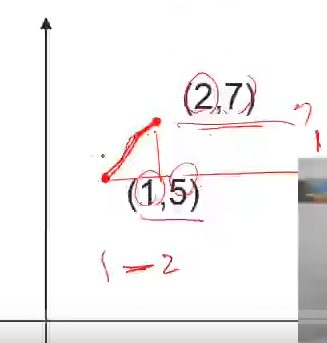

x = [1 2 5 2 1];
diff(x);
%(1,5)和(2,7)的斜率
x = [1 2];y = [5 7];
slope = diff(y)./diff(x);
x0 = 0.5*pi;h = 0.01;
x = [x0 x0+h];
y = [sin(x0) sin(x0+h)];
m = diff(y)./diff(x)exercise

代码:
%% exercise
for i = [1:1:7]x = [pi/2 pi/2+0.1^i];y = sin(x);disp(diff(y)./diff(x));
end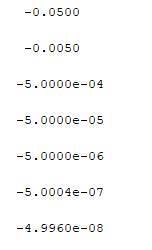
如何找0 2*pi区间的f'呢?
h = 0.1;
x = 0:h:2*pi;
y = sin(x);m = diff(y)./diff(x);
plot(x,y);hold on;
plot(0:h:2*pi-h,m);
legend('sin(x)','sin(x)''')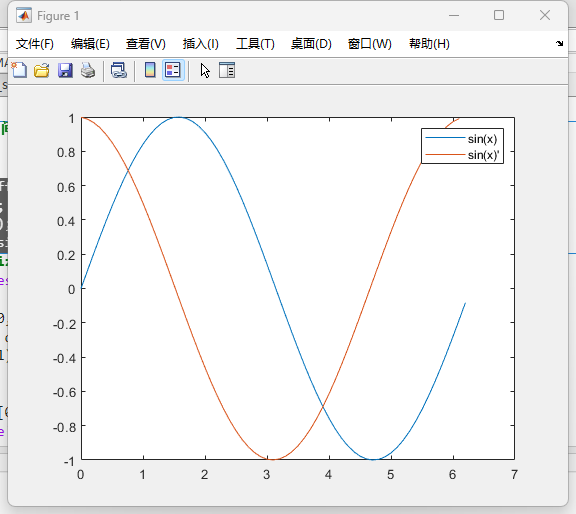
区间

various step size
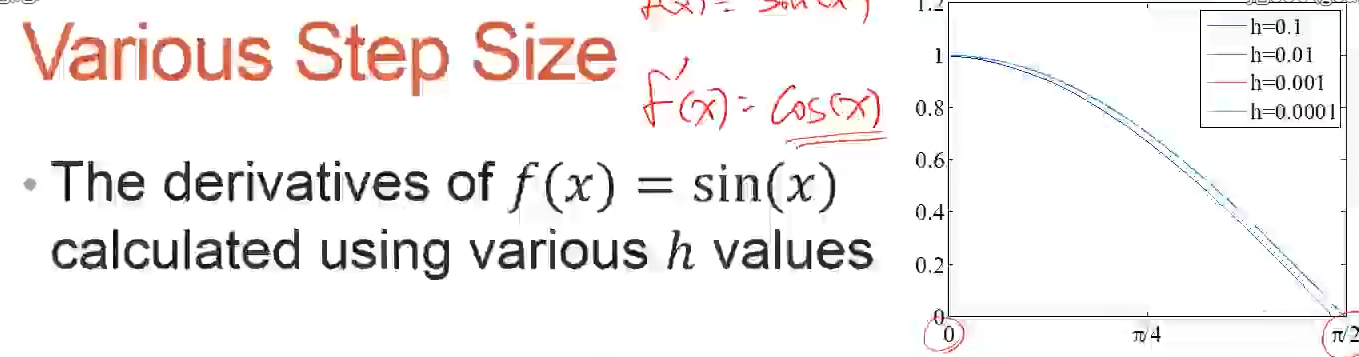
g = colormap("lines");hold on;
for i = 1:4x = 0:power(10,-i):pi;y =sin(x);m = diff(y)./diff(x);plot(x(1:end-1),m,'Color',g(i,:));
end
hold off;
set(gca, 'XLim', [0, pi/2]); set(gca, 'YLim', [0, 1.2]);%设置坐标轴范围
set(gca, 'FontSize', 18); %坐标轴标签和字体大小为18set(gca, 'XTick', 0:pi/4:pi/2);%x轴设置范围
set(gca, 'XTickLabel', {'0', 'p/4', 'p/2'});h = legend('h=0.1','h=0.01','h=0.001','h=0.0001');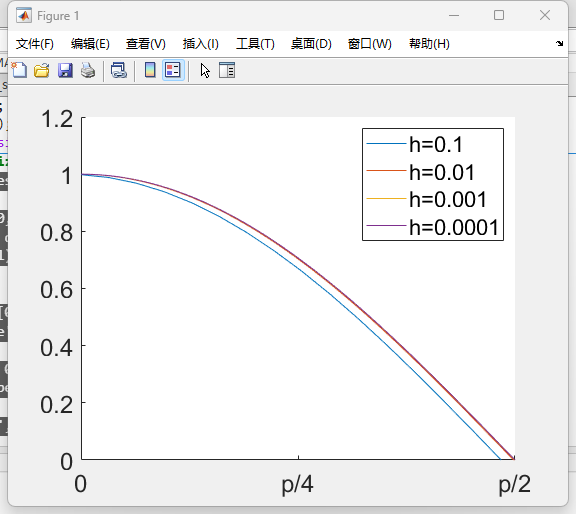
二次微分和三次微分
很简单,就是微分再微分
%% 二次微分和三次微分 second and third derivatives
x = -1:0.005:2;y = x.^3;
m = diff(y)./diff(x);
m2 = diff(m)./diff(x(1:end-1));%二次微分plot(x,y,x(1:end-1),m,x(1:end-2),m2);
xlabel('x','FontSize',18);
ylabel('y','FontSize',18);
legend('f(x)=x^3', ...'f''(x)','f''''(x)');
set(gca,'FontSize',18);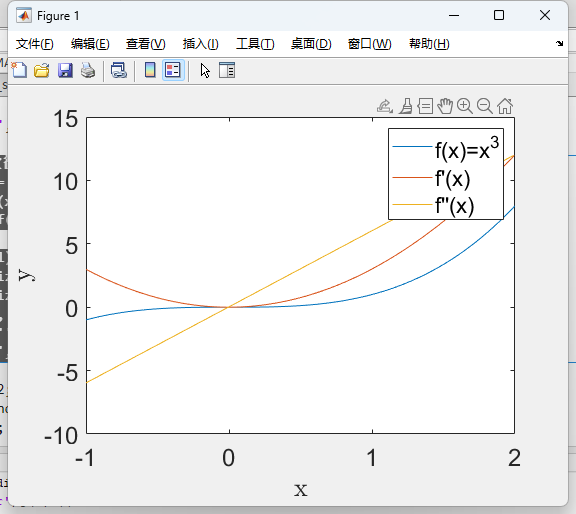

数值积分

求面积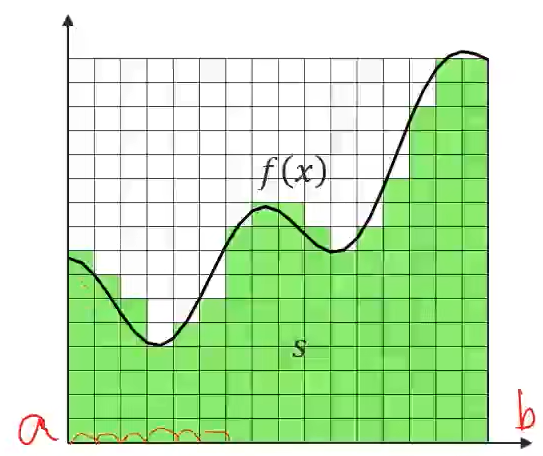
两个方法:
1.中点法则
2.梯形法则
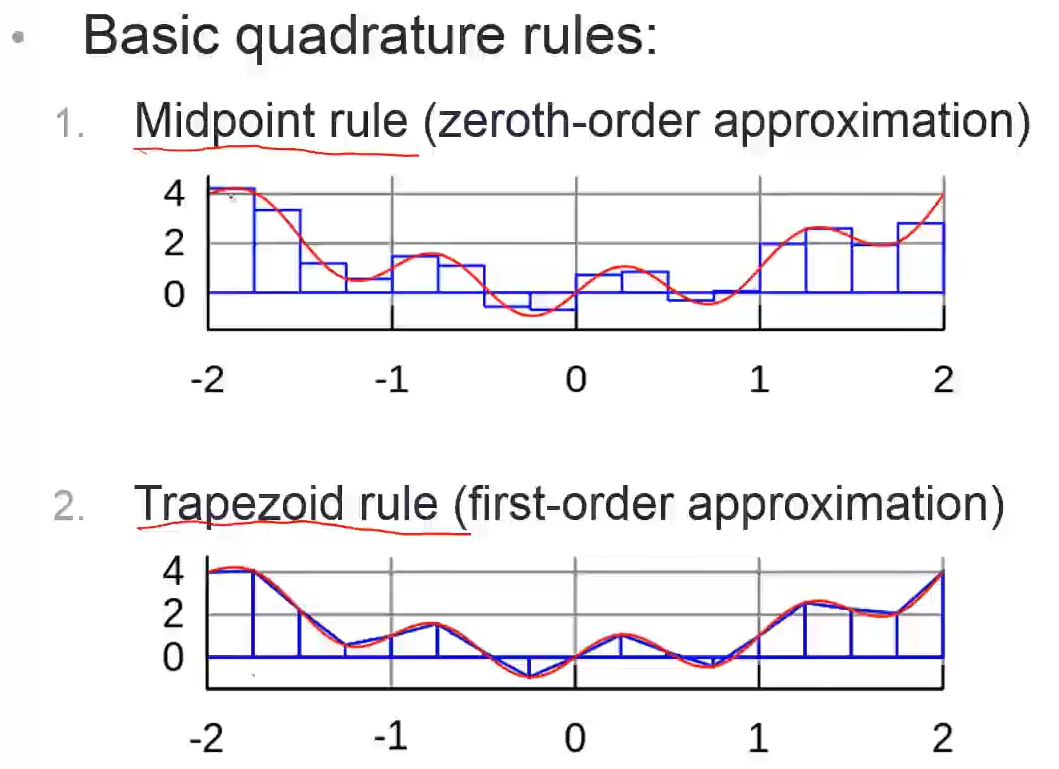
Midpoint Rule中点法则
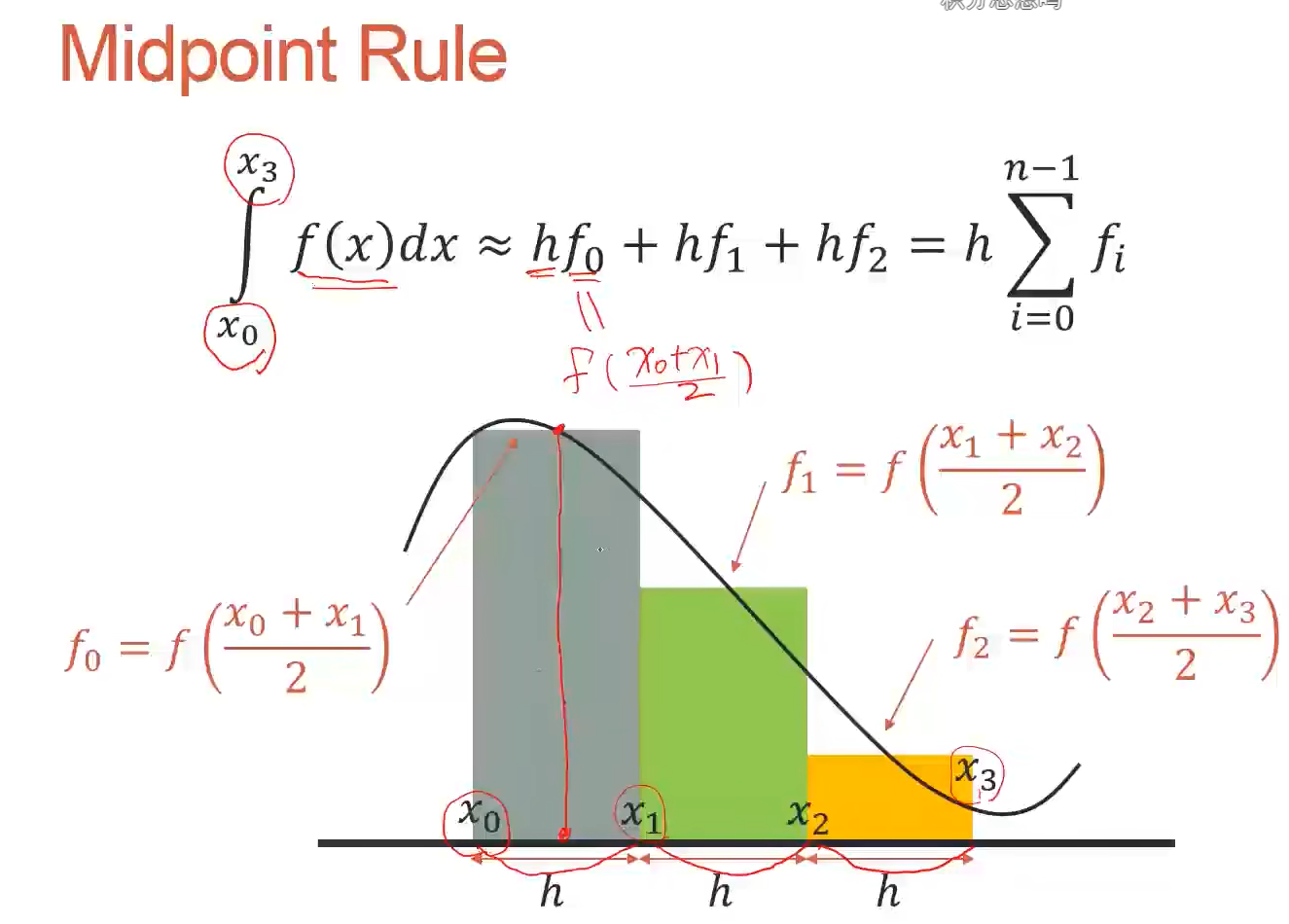
代码实现:
h = 0.05;x = 0:h:2;
midpoint = (x(1:end-1)+x(2:end))./2;
y = 4*midpoint.^3;
s = sum(h*y);s
%理论上是16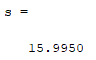
解释:
理论上是16,计算值15.9950
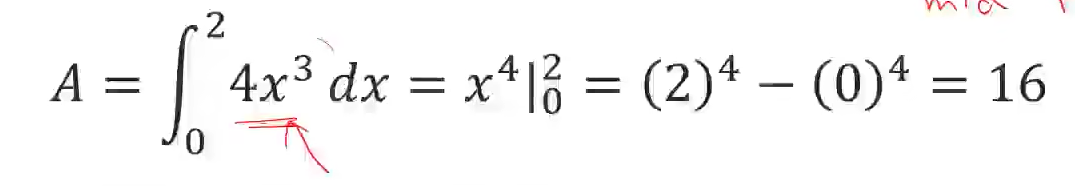

Trapezoid Rule梯形法则
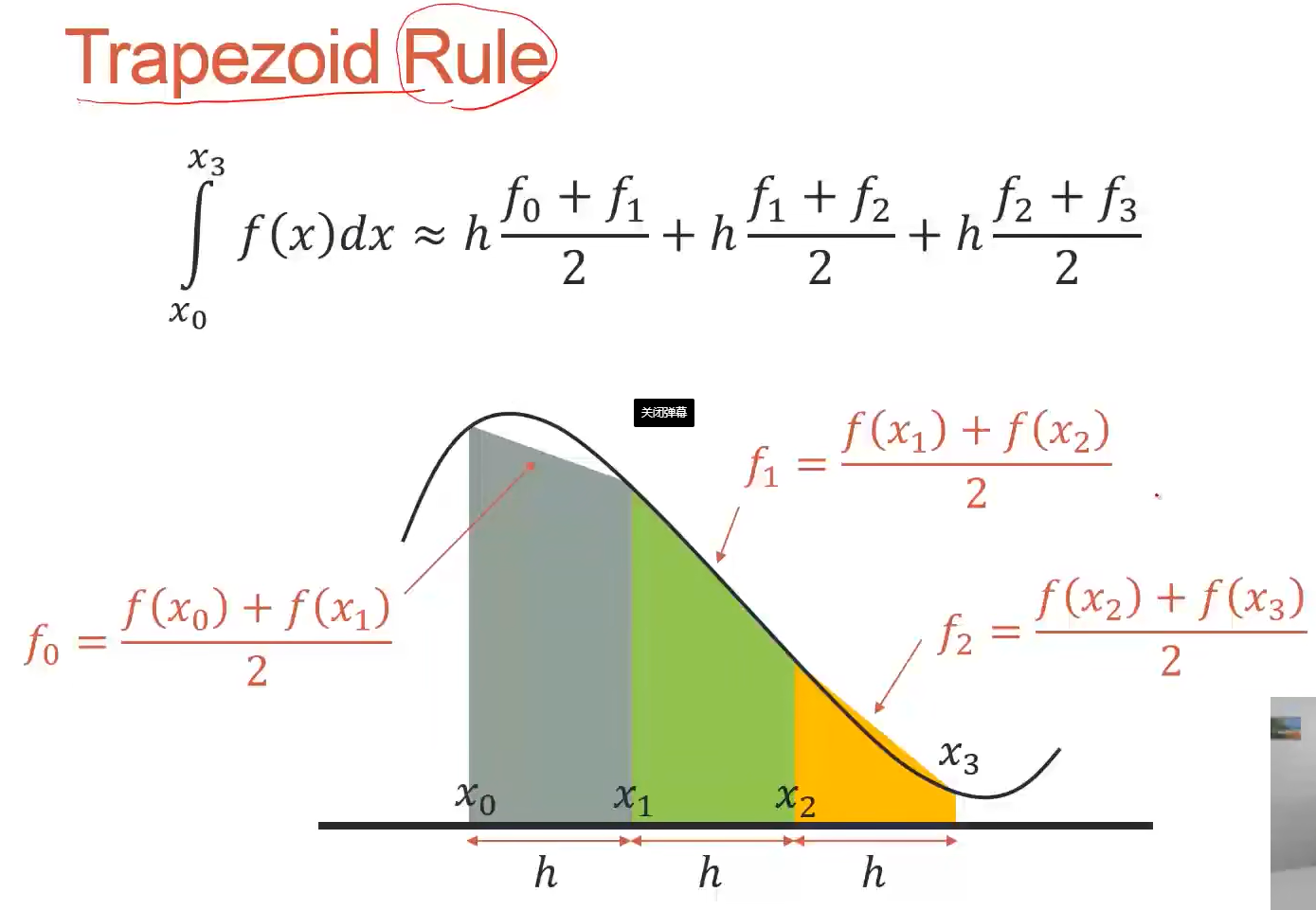
代码:
h = 0.05;x = 0:h:2;y = 4*x.^3;
s = h*trapz(y)
%可以自己算trapz
trapezoid = (y(1:end-1)+y(2:end))/2;
s = h*sum(trapezoid);结果:

辛普森公式simpson’s Rule
h = 0.05;x = 0:h:2;y = 4*x.^3;
s = h/3*(y(1)+2*sum(y(3:2:end-2)))+...4*sum(y(2:2:end))+y(end);%有这个规律,我写了手稿comparison
结果直接就是16
公式为什么是这个,我写了手稿:

匿名函数传递
function [y] = xy_plot(input,x)y = input(x);plot(x,y,'r--');
xlabel('x');ylabel('function(x)');
end在输入@sin作为y,懒得再在matlab弄了
integral

y = @(x) 1./(x.^3-2*x-5);
integral(y,0,2)
%sin(x)
y = @(x) sin(x)
integral(y,0,2)双重积分double和三重积分integrals

累死我了,感觉头晕目眩了
