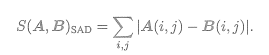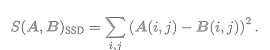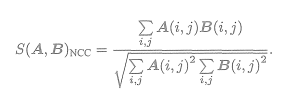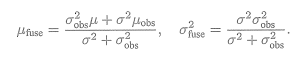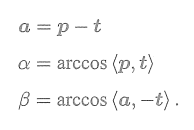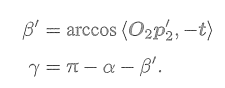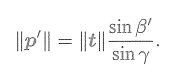当前位置：首页 > news >正文

视觉SLAM第12讲：建图

news 2025/9/19 5:42:51

目录

12.1 概述

12.2 单目稠密重建

12.2.1 立体视觉

12.2.2 极线搜索与块匹配

12.2.3 高斯分布的深度滤波器

12.3 实践：单目稠密重建

1.dense_mapping.cpp

2.CMakeLists.txt

3.运行结果

12.3.2 像素梯度问题

12.3.3 逆深度

12.3.4 图像间的变换

12.3.5 并行化：效率问题

12.3.6 其他的改进

12.4 RGB-D稠密建图

12.4.1 实践：点云建图

1.pointcloud_mapping.cpp

2.CMakeLists.txt

3.运行

4.注意事项

12.4.2 从点云重建网络

1.surfel_mapping.cpp

2.运行结果

3.注意事项

12.4.3 实践：八叉树地图

1.octomap_mapping.cpp

2.CMakeLists.txt

3.运行结果

4.注意事项

目标：

1.理解单目SLAM中稠密深度估计的原理；

2.通过实验了解单目稠密重建的过程；

3.了解几种RGB-D重建中的地图形式。

本讲介绍建图部分的算法。在前端和后端中，重点关注同时估计相机运动轨迹与特征点空间位置的问题。然而，在实际使用SLAM时，除了对相机本体进行定位，还存在许多其他的需求。例如，考虑放在机器人上的SLAM，那么我们会希望地图能够用于定位、导航、避障和交互，特征点地图显然不能满足所有的需求。所以，本讲我们将更详细地讨论各种形式的地图，并指出目前视觉SLAM地图中存在的缺陷。

12.1 概述

建图，本应该是SLAM 的两大目标之一——因为SLAM被称为同时定位与建图。但是直到现在，我们讨论的都是定位问题，包括通过特征点的定位、直接法的定位，以及后端优化。那么，这是否暗示建图在SLAM里没有那么重要，所以直到本讲才开始讨论呢?
答案是否定的。事实上，在经典的SLAM模型中，我们所谓的地图，即所有路标点的集合。一旦确定了路标点的位置，就可以说我们完成了建图。于是，前面说的视觉里程计也好，BA也好，事实上都建模了路标点的位置，并对它们进行了优化。从这个角度上说，我们已经探讨了建图问题。那么为何还要单独介绍建图呢?
这是因为人们对建图的需求不同。SLAM作为一种底层技术，往往是用来为上层应用提供信息的。如果上层是机器人，那么应用层的开发者可能希望使用SLAM做全局的定位，并且让机器人在地图中导航——例如扫地机需要完成扫地工作，希望计算一条能够覆盖整张地图的路径。或者，如果上层是一个增强现实设备，那么开发者可能希望将虚拟物体叠加在现实物体之中，特别地，还可能需要处理虚拟物体和真实物体的遮挡关系。
我们发现，应用层面对于“定位”的需求是相似的，希望SLAM提供相机或搭载相机的主体的空间位姿信息。而对于地图，则存在着许多不同的需求。从视觉SLAM的角度看，“建图”
是服务于“定位”的；但是从应用层面看，“建图”明显带有许多其他的需求。关于地图的用处
我们大致归纳如下：

（1）定位。定位是地图的一项基本功能。在前面的视觉里程计部分，我们讨论了如何利用局
部地图实现定位。在回环检测部分，我们也看到，只要有全局的描述子信息，我们也能通过回环检测确定机器人的位置。我们还希望能够把地图保存下来，让机器人在下次开机后依然能在地图中定位，这样只需对地图进行一次建模，而不是每次启动机器人都重新做一次完整的SLAM
（2）导航。导航是指机器人能够在地图中进行路径规划，在任意两个地图点间寻找路径，然
后控制自己运动到目标点的过程。在该过程中，我们至少需要知道地图中哪些地方不可通过，而哪些地方是可以通过的。这就超出了稀疏特征点地图的能力范围，必须有另外的地图形式。稍后我们会说,这至少得是一种稠密的地图。
（3）避障。避障也是机器人经常碰到的一个问题。它与导航类似，但更注重局部的、动态的
障碍物的处理。同样，仅有特征点，我们无法判断某个特征点是否为障碍物，所以需要稠密地图。
（4）重建。有时，我们希望利用SLAM获得周围环境的重建效果。这种地图主要用于向人展
示，所以希望它看上去比较舒服、美观。或者，我们也可以把该地图用于通信，使其他人能够远程观看我们重建得到的三维物体或场景——例如三维的视频通话或者网上购物等。这种地图亦是稠密的，并且还对它的外观有一些要求。我们可能不满足于稠密点云重建，更希望能够构建带纹理的平面，就像电子游戏中的三维场景那样。
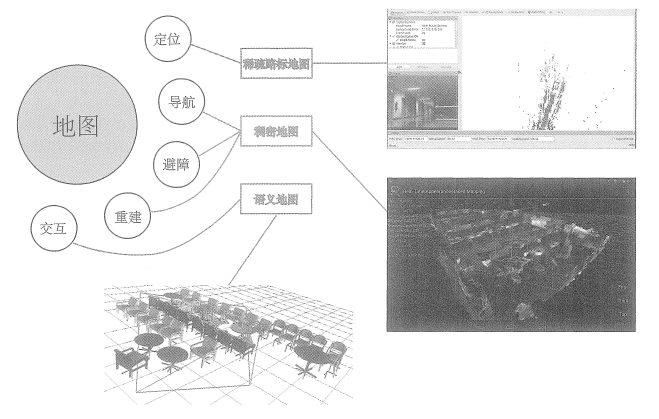
（5）交互。交互主要指人与地图之间的互动。例如,在增强现实中,我们会在房间里放置虚拟的物体，并与这些虚拟物体之间有一些互动——例如我们会点击墙面上放着的虚拟网页浏览器来观看视频,或者向墙面投掷物体,希望它们有（虚拟的）物理碰撞。另外，机器人应用中也会有与人、与地图之间的交互。例如，机器人可能会收到命令“取桌子上的报纸”，那么，除了有环境地图，机器人还需要知道哪一块地图是“桌子”，什么叫作“之上”，什么叫作“报纸”。这就需要机器人对地图有更高层面的认知——也称为语义地图。

下图形象地解释了上面讨论的各种地图类型与用途之间的关系。我们之前的讨论，基本集中于“稀疏路标地图”部分，还没有探讨稠密地图。所谓稠密地图是相对于稀疏地图而言的。稀疏地图只建模感兴趣的部分，也就是前面说了很久的特征点（路标点)。而稠密地图是指建模所有看到过的部分。对于同一张桌子，稀疏地图可能只建模了桌子的四个角，而稠密地图则会建模整个桌面。虽然从定位角度看，只有四个角的地图也可以用于对相机进行定位，但由于我们无法从四个角推断这几个点之间的空间结构，所以无法仅用四个角完成导航、避障等需要稠密地图才能完成的操作。

从上面的讨论中可以看出，稠密地图占据着一个非常重要的位置。于是，剩下的问题是：通过视觉 SLAM能建立稠密地图吗？如果能，怎么建呢？

12.2 单目稠密重建

12.2.1 立体视觉

视觉SLAM的稠密重建问题是本讲的第一个重要话题。相机，被认为是只有角度的传感
器（Bearing only）。单幅图像中的像素，只能提供物体与相机成像平面的角度及物体采集到的亮度,而无法提供物体的距离（Range）。而在稠密重建中，我们需要知道每一个像素点（或大部分像素点）的距离，对此大致上有如下解决方案：

（1）使用单目相机，估计相机运动，并且三角化计算像素的距离
（2）使用双目相机，利用左右目的视差计算像素的距离（多目原理相同）

（3）使用RGB-D相机直接获得像素距离

前两种方式称为立体视觉（Stereo Vision），其中移动单目相机的又称为移动视角的立体视觉（Moving View Stereo，MVS）。相比于RGB-D直接测量的深度，使用单目和双目的方式对深度获取往往是“费力不讨好”的——计算量巨大，最后得到一些不怎么可靠的R深度估计。当然，RGB-D也有一些量程、应用范围和光照的限制，不过相比于单目和双目的结果，使用RGB-D进行稠密重建往往是更常见的选择。而单目、双目的好处是，在目前RGB-D还无法被很好地应用的室外、大场景场合中，仍能通过立体视觉估计深度信息。

话虽如此，本节我们将带领读者实现一遍单目的稠密估计，体验为何说它是费力不讨好的。我们从最简单的情况讲起：在给定相机轨迹的基础上，如何根据一段时间的视频序列估计某幅图像的深度。换言之，我们不考虑SLAM，先来考虑略为简单的建图问题。
假定有一段视频序列，我们通过某种魔法得到了每一帧对应的轨迹（当然也很可能是由视觉里程计前端估计所得）。现在以第一幅图像为参考帧，计算参考帧中每个像素的深度（或者距离）。首先,请回忆在特征点部分我们是如何完成该过程的：

（1）对图像提取特征，并根据描述子计算特征之间的匹配。换言之，通过特征，我们对某一
个空间点进行了跟踪，知道了它在各个图像之间的位置。
（2）由于无法仅用一幅图像确定特征点的位置，所以必须通过不同视角下的观测估计它的深
度，原理即前面讲过的三角测量。

在稠密深度图估计中，不同之处在于，我们无法把每个像素都当作特征点计算描述子。因此，稠密深度估计问题中，匹配就成为很重要的一环：如何确定第一幅图的某像素出现在其他图里的位置呢？这需要用到极线搜索和块匹配技术。当我们知道了某个像素在各个图中的位置，就能像特征点那样，利用三角测量法确定它的深度。不过不同的是，在这里要使用很多次三角测量法让深度估计收敛，而不仅使用一次。我们希望深度估计能够随着测量的增加从一个非常不确定的量，逐渐收敛到一个稳定值。这就是深度滤波器技术。所以，下面的内容将主要围绕这个主题展开。

12.2.2 极线搜索与块匹配

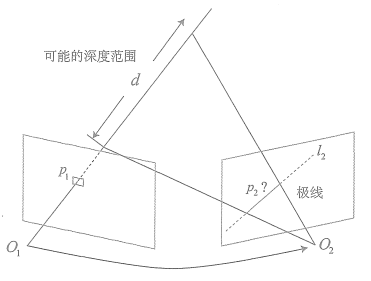
我们先来探讨不同视角下观察同一个点产生的几何关系。这非常像在7.3节讨论的对极几何关系。如图，左边的相机观测到了某个像素p1。由于这是一个单目相机，无从知道它的深度，所以假设这个深度可能在某个区域之内，不妨说是某最小值到无穷远之间。
因此，该像素对应的空间点就分布在某条线段（本例中是射线）上。从另一个视角（右侧相机）看，这条线段的投影也形成图像平面上的一条线，我们知道这称为极线。当知道两部相机间的运动时，这条极线也是能够确定的。那么问题就是：极线上的哪一个点是我们刚才看到的点呢？

重复一遍，在特征点方法中，通过特征匹配找到了p2的位置。然而现在我们没有描述子，所以只能在极线上搜索和p1长得比较相似的点。再具体地说，我们可能沿着第二幅图像中的极线的某一头走到另一头，逐个比较每个像素与p1的相似程度。从直接比较像素的角度来看，这种做法和直接法有异曲同工之妙。

在直接法的讨论中我们了解到，比较单个像素的亮度值并不一定稳定可靠。一件很明显的事情就是：万一极线上有很多和p1相似的点，怎么确定哪一个是真实的呢？这似乎回到了我们在回环检测中说到的问题：如何确定两幅图像（或两个点）的相似性？回环检测是通过词袋来解决的，但这里由于没有特征，所以只好寻求另外的解决途径。
一种直观的想法是：既然单个像素的亮度没有区分性，是否可以比较像素块呢？我们在周围取一个大小为的小块，然后在极线上也取很多同样大小的小块进行比较，就可以在一定程度上提高区分性。这就是所谓的块匹配。在这个过程中，只有假设在不同图像间整个小块的灰度值不变，这种比较才有意义。所以算法的假设，从像素的灰度不变性变成了图像块的灰度不变性——在一定程度上变得更强了。

现在我们取了p1周围的小块，并且在极线上也取了很多个小块。不妨把p1周围的小块记成 $A\epsilon R^{w*w}$ ，把极线上的n个小块记成 $B_{i},i=1,...,n$ 。那么，如何计算小块与小块间的差异呢？有若干种的解决办法：

（1）SAD（Sum of Absolute Difference）

取两个小块的差的绝对值之和

（2）SSD

平方和

（3）NCC（Normalized Cross Correlation，归一化互相关）

这种方式比前两种要复杂，它计算的是两个小块的相关性

请注意，由于这里用的是相关性，所以相关性接近0表示两幅图像不相似，接近1表示相似。前面两种距离则是反过来的，接近0表示相似，而大的数值表示不相似。

和我们遇到过的许多情形一样，这些计算方式往往存在一个精度——效率之间的矛盾。精度好的方法往往需要复杂的计算，而简单的快速算法又往往效果不佳。这需要我们在实际工程中进行取舍。另外，除了这些简单版本，我们可以先把每个小块的均值去掉，称为去均值的SSD、去均值的NCC，等等。去掉均值之后，允许像“小块B比A整体上亮一些，但仍然很相似”这样的情况，因此比之前的更可靠。

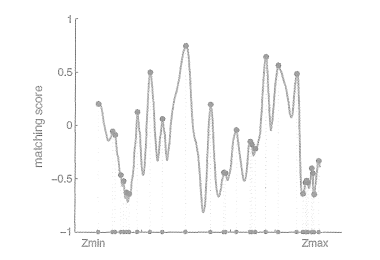
现在，我们在极线上计算了A与每一个的相似性度量。为了方便叙述，假设我们用了NCC，那么，将得到一个沿着极线的NCC分布。这个分布的形状取决于图像数据，如图所示。在搜索距离较长的情况下，通常会得到一个非凸函数：这个分布存在许多峰值，然而真实的对应点必定只有一个。在这种情况下，我们会倾向于使用概率分布描述深度值，而非用某个单一的数值来描述深度。于是，我们的问题就转到了在不断对不同图像进行极线搜索时，我们估计的深度分布将发生怎样的变化——这就是所谓的深度滤波器。

12.2.3 高斯分布的深度滤波器

对像素点深度的估计，本身也可建模为一个状态估计问题，于是就自然存在滤波器与非线性优化两种求解思路。虽然非线性优化效果较好，但是在SLAM这种实时性要求较强的场合，考虑到前端已经占据了不少的计算量，建图方面则通常采用计算量较少的滤波器方式。这也是本节讨论深度滤波器的目的。

对深度的分布假设存在若干种不同的做法。一方面，在比较简单的假设条件下，可以假设深度值服从高斯分布，得到一种类卡尔曼式的方法（但实际上只是归一化积，我们稍后会看到）。本着简单易用的原则，我们演示高斯分布假设下的深度滤波器，然后把均匀——高斯混合分布的滤波器作为习题。

设某个像素点的深度d服从

每当新的数据到来，我们都会观测到它的深度。同样，假设这次观测也是一个高斯分布



于是，我们的问题是，如何使用观测的信息更新原先d的分布。这正是一个信息融合问题。根据附录A，我们明白两个高斯分布的乘积依然是一个高斯分布。设融合后的d的分布为，那么根据高斯分布的乘积，有



由于我们仅有观测方程没有运动方程，所以这里深度仅用到了信息融合部分，而无须像完整的卡尔曼那样进行预测和更新（当然，可以把它看成“运动方程为深度值固定不动”的卡尔曼滤波器）。可以看到融合的方程确实浅显易懂，不过问题仍然存在：如何确定我们观测到深度的分布呢？即如何计算 $\mu _{obs},\sigma _{obs}$ 呢？

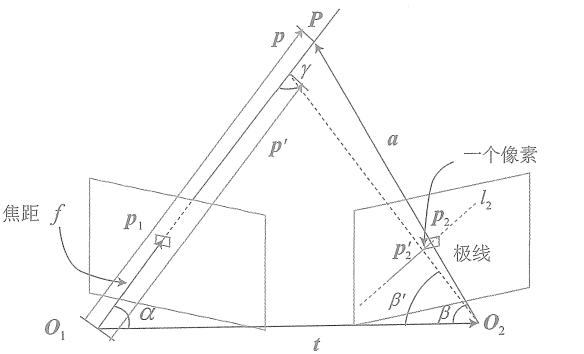
考虑某次极线搜索，我们找到了p1对应的点p2，从而观测到了p1的深度值，认为p1对应的三维点为P。从而，可记 $O_{1}P$ 为p， $O_{1}O_{2}$ 为相机的平移t， $O_{2}P$ 记为a。并且，把这个三角形的下面两个角记作 $\alpha ,\beta$ 。现在，考虑极线 $l_{2}$ 上存在一个像素大小的误差，使得角 $\beta$ 变成了 $\beta^{{}'}$ ，而 $p_{2}$ 也变成了 $p_{2}{}'$ ，并记上面那个角为 $\gamma$ 。我们要问的是，这个像素的误差会导致 $p_{}{}'$ 与 $p_{}{}$ 产生多大的差距呢？



  这是一个典型的几何问题。我们来列写这些量之间的几何关系。

有

对 $p_{2}{}$ 扰动一个像素，将使得 $\beta$ 产生一个变化量，成为 $\beta{}'$ 。

根据几何关系，有



于是，由正弦定理， $p_{}{}{}'$ 的大小可以求得



由此，我们确定了由单个像素的不确定引起的深度不确定性。如果认为极线搜索的块匹配仅有一个像素的误差，

那么就可以设