2025高教杯数学建模大赛全流程，从数据处理、建模到模型评价
有些第一次参加数学竞赛的同学可能觉得自己还没准备好，临近比赛感到紧张很正常，但需调整心态——数学建模比赛本就是学习过程，遇到不会的知识及时搜索、现学现用即可，直接参赛就是最好的学习方式。
无论题目是怎样的，掌握核心的模型及数据处理方法都是关键的。今天将按流程分别介绍数学建模过程中可能用到的处理方法及模型算法。
数学建模常用方法大致可分为四大部分：数据处理、描述性统计、模型算法、模型评价，如下图：
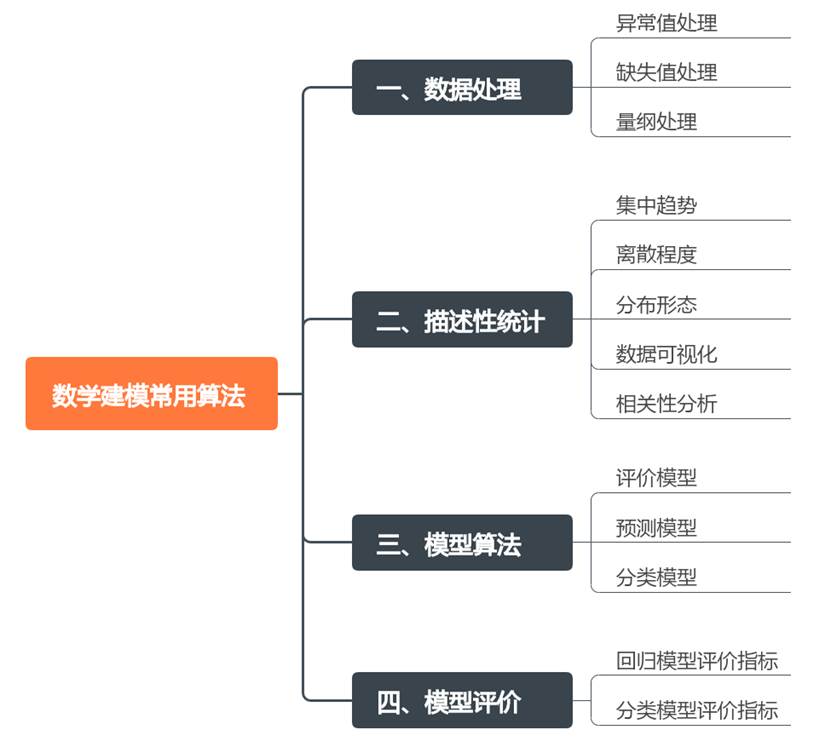
接下来将分别进行介绍说明。
一、数据处理
国赛的数据处理是指进行数据的清洗和变换，预处理的质量会直接影响到后续建模和预测的准确性。数据清洗也就是我们常说的缺失值处理和异常值处理，数据变换是指对数据进行标准化、归一化等无量纲化处理，常见的数据预处理方式见下图：
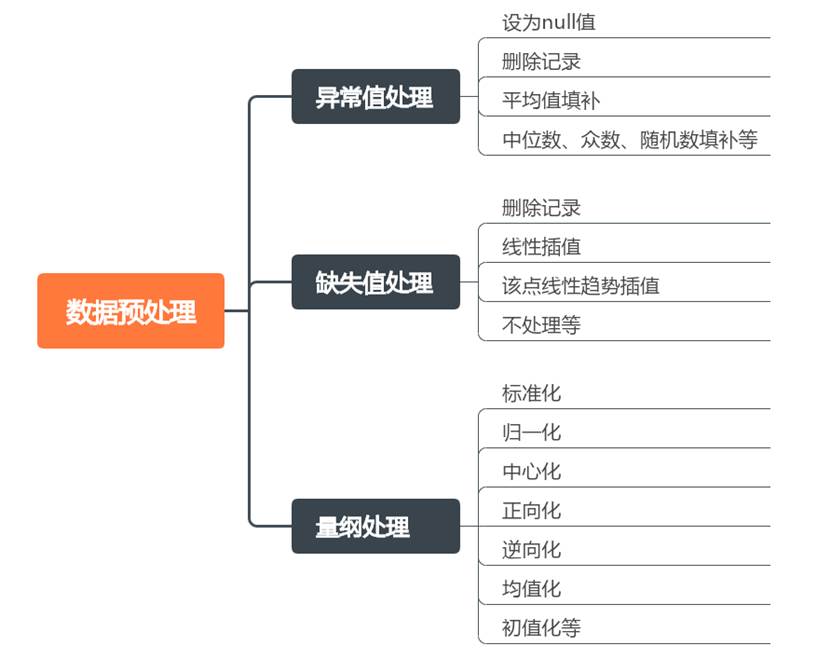
1、异常值处理
异常值是指显著偏离主体数据的观测值，可能引发模型偏差、统计效力下降及分布假设失效。
（1）检测异常值
检测异常值的常用方法主要包括以下两类：统计方法（如Z-score法、IQR箱线图法）、可视化方法（如散点图、箱线图）。Z-score通过标准差识别偏离均值过远的点；IQR箱线图则基于四分位距划定正常范围，之外的点视为异常。
（2）处理异常值的方法
异常值处理通常有以下4种方式：
| 异常值处理 | 说明 |
| 删除 | 如果异常值是随机错误导致的，或者异常值的数量非常少，以考虑直接删除这些异常值。 |
| 替换 | 用均值、中位数或众数替换异常值。 |
| 转换 | 对数据进行对数转换、Box-Cox转换等，减少异常值的影响。 |
| 保留 | 如果异常值是重要的数据点，这时可以选择保留。 |
2、缺失值处理
对缺失值进行处理方法通常有删除、填充、插值3类方法，说明如下表：
| 方法名称 | 描述 |
| 删除行 | 从数据集中删除含有缺失值的整行数据。 |
| 删除列 | 如果某一列缺失值过多，考虑删除整列。 |
| 均值/中位数/众数填充 | 使用特征的均值、中位数（适用于数值型变量）或众数（适用于分类变量）来填充缺失值。 |
| 固定值填充 | 用一个固定的值（如0、-1或特定标记）填充缺失值。 |
| 线性插值 | 在时间序列数据中使用通过相邻数据点进行线性内插。 |
| 该点线性趋势插值 | 利用缺失点前后的数据来估计缺失值，假设数据在短期内呈线性变化。 |
对于异常值和缺失值的处理，可以使用SPSSAU【数据处理】模块的【异常值】方法进行处理，操作如下：
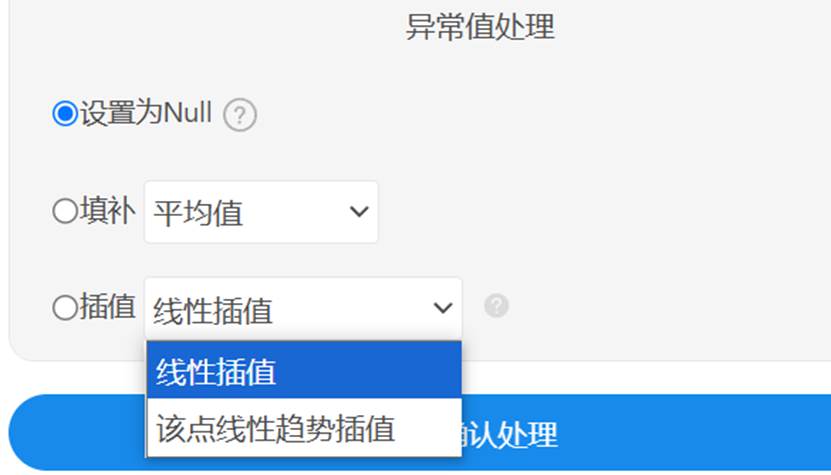
点击下方链接跳转至相应方法帮助手册：
异常值处理
3、量纲处理
数学建模很多算法在使用前均需要进行数据处理。例如熵值法计算权重前需要对正向指标进行正向化处理，负向指标进行逆向化处理。SPSSAU提供17种数据无量纲化处理方法，常用的如标准化、中心化、归一化、均值化、正向化、逆向化等，说明如下：
| 类型 | 意义 |
| 标准化（S） | 让数据变成平均值为0，标准差为1 |
| 中心化（C） | 让数据变成平均值为0 |
| 归一化（MMS） | 让数据压缩在【0，1】范围内 |
| 均值化（MC） | 以平均值作为标准进行对比 |
| 正向化（MMS） | 让数据压缩在【0，1】范围内 |
| 逆向化（NMMS） | 让数据压缩在【0，1】范围内，且数据方向颠倒 |
| 适度化（M） | 让数据进行适度化处理 |
| 区间化（Interval） | 让数据压缩在自己希望的范围内 |
| 初值化（Init） | 数据除以第1个数字 |
| 最小值化（MinS） | 以最小值作为标准进行对比 |
| 最大值化（MaxS） | 以最大值作为标准进行对比 |
| 求和归一化（SN） | 数据表达总和的比例 |
| 平方和归一化（SSN） | 数据表达平方和的比例 |
| 固定值化(CloseFixedValue) | 固定值化时离FixedValue越近越好 |
| 偏固定值化(OffFixedValue) | 偏固定值化时离FixedValue越远越好 |
| 近区间化(CloseInterval) | 近区间化时离（p,q）区间越近越好 |
| 偏区间化(OffInterval) | 偏区间化时离（p,q）区间越远越好 |
在SPSSAU【数据处理】模块选择【生成变量】可对数据进行处理，操作如下图：
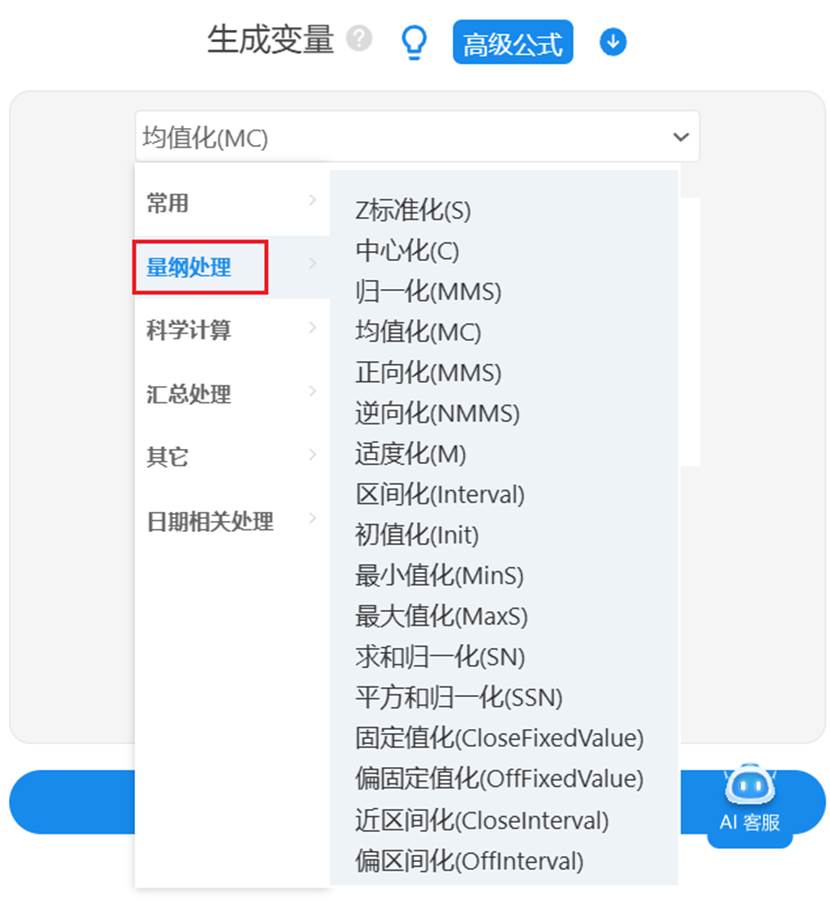
在研究时具体应该使用哪一种处理方式呢，其实并没有固定的要求，而是结合建模实际情况进行选择，关于数据无量纲处理的更多内容可以查看下文：
数据处理——17种无量纲化处理方法说明
生成变量帮助手册
二、描述性统计
描述性统计是数学建模的关键预处理步骤，通过量化分析（均值/方差）和可视化工具（箱线图/直方图）等快速把握数据分布特征与变量关联性，为后续建模提供数据质量评估与策略依据。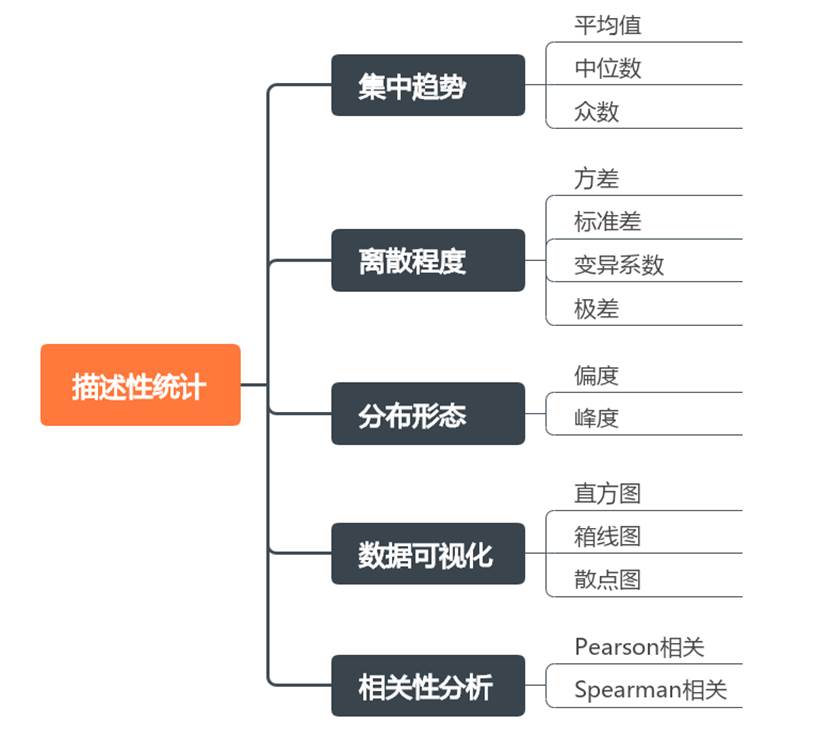
描述性统计分析方法整理表格如下：
| 分析类型 | 统计量 | 用途 |
| 集中趋势 | 均值 | 反映数据的平均水平 |
| 中位数 | 不受极端值影响，反映数据的中心位置 | |
| 众数 | 反映数据的集中点，适用于分类数据 | |
| 离散程度 | 方差 | 反映数据的离散程度 |
| 标准差 | 以原数据的单位描述离散程度 | |
| 变异系数 | 比较不同量纲数据的离散程度 | |
| 极差 | 快速了解数据的分布范围 | |
| 分布形态 | 偏度 | 判断分布的偏斜方向和程度 |
| 峰度 | 判断分布的尖峭或平坦程度 | |
| 数据可视化 | 直方图 | 直观显示数据分布形态 |
| 箱线图 | 识别异常值，比较多组数据 | |
| 散点图 | 观察变量间的相关性和模式 | |
| 相关性分析 | Pearson相关系数 | 适用于连续变量，且变量间呈线性关系、服从正态分布时效果较好 |
| Spearman相关系数 | 适用于不满足线性关系或不服从正态分布的数据，对异常值相对稳健 |
描述性统计分析基本步骤：
- 计算基本统计量：均值、中位数、标准差等
- 绘制可视化图表：直方图、箱线图等
- 分析数据分布：是否正态分布，是否有偏态
- 检查相关性：查看变量间的关系
点击下方链接跳转至相应方法帮助手册：
- 描述分析
- 正态性检验
- 直方图
- 箱线图
- 散点图
- 相关分析
三、模型算法
数学建模关键的步骤就在于模型的选择与构建，根据问题的性质选择合适的模型类型，如数学建模中常见的三大模型评价模型、预测模型、分类模型。
1、评价模型
评价模型是数学建模中用于量化分析、比较和优选方案的工具，通过系统化的指标体系和算法对复杂问题进行客观评估。常用的方法如层次分析法、熵值法、TOPSIS法等，说明如下表：
| 方法名称 | 简要介绍 |
| AHP层次分析法 | 通过构建层次结构模型，对指标进行两两比较，确定权重，最终得出评价对象的综合得分。适用于多准则决策问题。 |
| 熵值法 | 根据指标数据的离散程度（信息熵）计算权重，信息熵越小，权重越大，是一种客观赋权方法。 |
| TOPSIS法 | 通过计算评价对象与理想解和负理想解的距离，进行排序，选择最优方案。适用于多属性决策分析。 |
| 模糊综合评价 | 利用模糊数学理论，将定性指标转化为定量评价，适用于处理评价过程中存在的不确定性和模糊性问题。 |
| 灰色关联法 | 通过分析评价对象与参考序列之间的关联度，判断其接近程度，适用于数据量少或信息不完全的情况。 |
| 数据包络分析（DEA） | 利用线性规划方法，评价具有相同类型多投入、多产出的决策单元之间的相对效率。 |
| 秩和比法（RSR） | 将指标排序后转化为秩次，计算秩和比，综合评价对象的优劣，适用于多指标综合评价。 |
点击下方链接跳转至相应方法帮助手册：
- AHP层次分析法
- 熵值法
- TOPSIS法
- 模糊综合评价
- 灰色关联法
- 数据包络分析DEA
- 秩和比法RSR
SPSSAU软件操作：
以熵值法为例，上传数据至SPSSAU平台，在【综合评价】模块选择【熵值法】，将变量拖拽至右侧分析框中，点击开始分析按钮即可得到分析结果：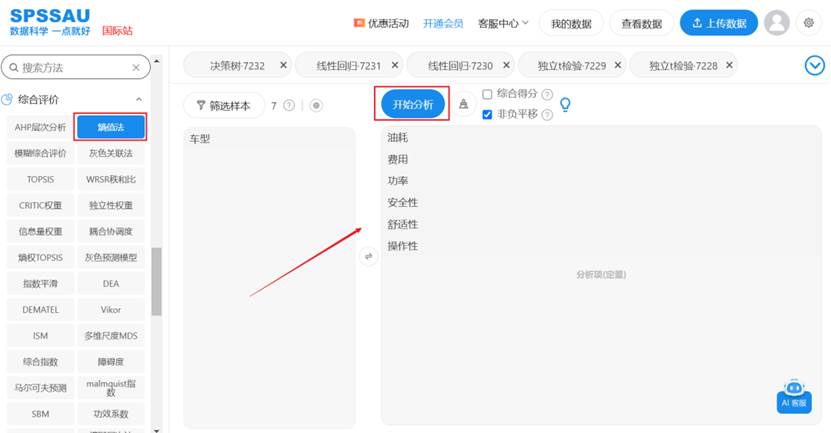
SPSSAU输出标准三线表分析结果如下，用户可直接将结果粘贴到建模论文中，无需手动调整格式：
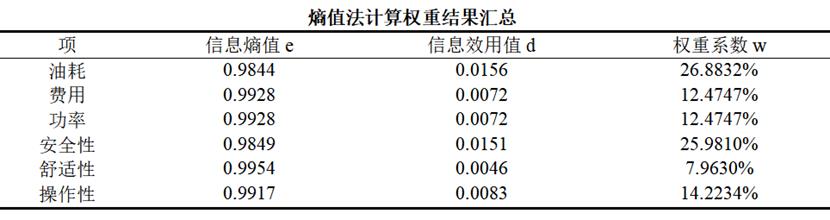更多权重计算和综合评价的方法可查看下方文章：
评价指标体系 | 15种权重计算与综合评价方法汇总
2、分类模型
分类模型是基于数学算法的数据划分工具，通过分析历史数据的特征规律，构建预测规则以实现新数据的自动归类。其核心是通过学习已知样本的分布模式，推断未知样本的类别归属。典型的方法包括聚类分析、判别分析、logistic回归、机器学习。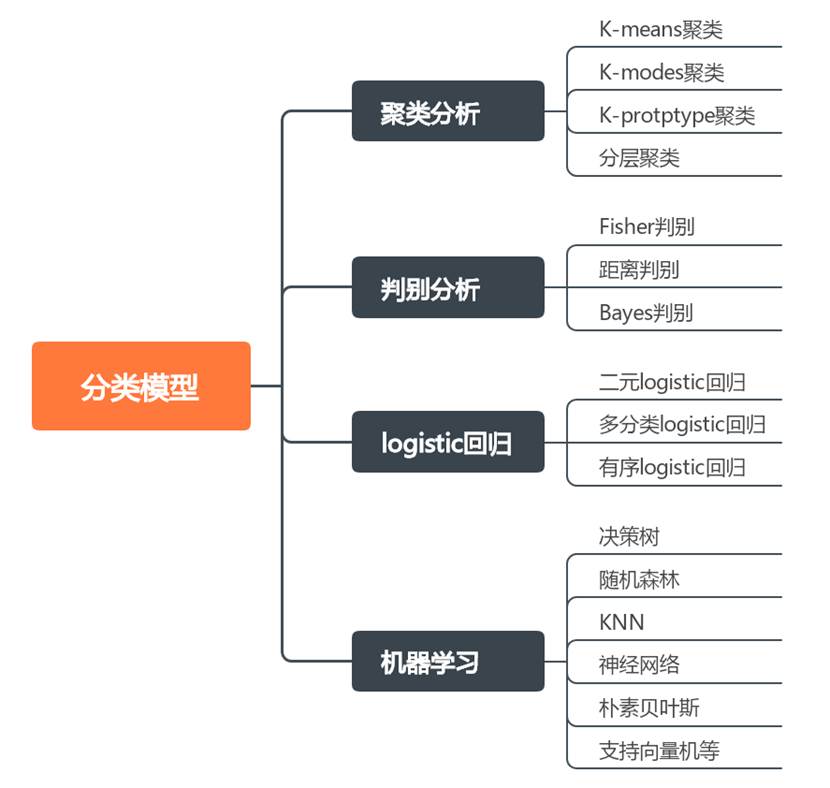
（1）聚类分析
聚类分析是一种无监督学习方法，通过将数据集中相似的对象自动分组，从而发现数据内在的结构与模式。常用的聚类分析分为K-means聚类、K-modes聚类、K-prototype聚类以及分层聚类。其中前三种聚类方法是按行聚类（R型聚类），分层聚类是按列聚类（Q型），最常用的为K-means聚类，各自适用场景说明如下表：
| 聚类方法 | 适用场景 |
| K-means聚类 | 数据为定量数据时使用 |
| K-modes聚类 | 数据为定类数据时使用 |
| K-prototype聚类 | 数据既有定量数据又有定类数据时使用 |
| 分层聚类 | 对定量数据进行按列聚类时使用 |
有关4种聚类方法的详细介绍，可以查看往期这篇文章以及SPSSAU帮助手册：
- 干货合集→聚类分析
- 聚类分析（R型聚类）
- 分层聚类（Q型聚类）
（2）判别分析
判别分析是一种基于已知分类样本建立判别函数，用于对新样本进行分类的统计方法，广泛应用于模式识别、机器学习和生物统计学等领域。判别分析有很多种，比如Fisher判别、距离判别、Beyes判别等，其中Fisher判别使用频率最高。
| 判别分析 | 说明 |
| Fisher判别 | 通过计算样本点与各个类别之间的距离，来确定样本点所属类别 |
| 距离判别 | 通过计算欧式距离，确定样本点所属类别 |
| Bayes判别 | 通过计算样本点各个特征的概率分布，来确定每个样本点所属类别 |
SPSSAU默认使用Fisher线性判别，点击下方链接跳转至相应方法帮助手册：
判别分析帮助手册
（3）logistic回归
logistic回归可以用于分类，它的核心思想是利用逻辑函数将线性回归的结果转化成一个概率值，这个概率值可以用来进行分类。logistic回归分析可细分为二元logistic回归、多分类logistic回归、有序logistic回归、条件logistic回归。各自适用场景说明如下表：
| logistic回归 | 适用场景 |
| 二元logistic回归 | Y值仅两个选项，分别是有和无之类的二分类数据 |
| 多分类logistic回归 | Y值的选项有多个，并且选项之间没有大小对比关系 |
| 有序logistic回归 | Y值的选项有多个，并且选项之间可以对比大小关系，选项具有对比意义 |
| 条件logistic回归 | Y值为二分类数据，通常用于处理配对数据，如成对取样、双胞胎、案例 - 对照研究等 |
点击下方链接跳转至相应方法帮助手册：
- 二元logistic回归
- 多分类logistic回归
- 有序logistic回归
- 条件logistic回归
（4）机器学习
机器学习算法中常用于分类的模型包括决策树、随机森林、KNN、神经网络、朴素贝叶斯、支持向量机等等。具体说明如下：
| 机器学习 | 说明 |
| 决策树 | 是一种基于树结构的分类模型，它通过训练数据集划分为若干个子集，从而实现对新数据的分类。 |
| 随机森林 | 是一种集成学习模型，通过构建多个决策树并将它们的预测结果进行投票，从而得到最终的分类结果。 |
| KNN | 是一种基于实例的学习算法，它将训练数据集中的最近邻样本作为新样本的预测依据 |
| 神经网络 | 是一种模拟人脑神经元结构的计算模型，通过多层神经元的组合和连接来实现对数据的分类。 |
| 朴素贝叶斯 | 是一种基于贝叶斯定理的分类模型，它假设特征之间相互独立。 |
| 支持向量机 | 是一种基于间隔最大化的分类模型，它通过在特征空间中找到一个最优超平面将不同类别的样本分隔开来。 |
| logistic回归 | 是一种广义线性回归模型，常用于二分类问题，通过Sigmoid函数将线性回归结果映射到0-1之间以得到分类概率。 |
| apriori关联分析 | 是一种用于数据挖掘的经典算法，其作用是找出数据中频繁出现的集合，进而辅助进行有效决策。 |
| XGBoost | 是高效的梯度提升树算法，模型加入正则化项、支持并行计算等，能有效处理过拟合，提升模型性能。 |
| GBDT | 梯度提升决策树，通过构建一系列弱决策树，利用梯度下降思想迭代，将各树预测结果累加得到强预测模型。 |
| Adaboost | 自适应增强算法，根据前一轮模型预测误差调整样本权重，使错误分类样本在后续训练中受更多关注，组合多个弱分类器形成强分类器。 |
| 极端随机树 | 与随机森林类似的集成学习方法，构建决策树时随机选择特征子集和分裂点，增加随机性以防止过拟合。 |
| CatBoost | 基于梯度提升的算法，针对类别型特征优化，能自动处理类别特征，通过排序提升和防止过拟合机制提高模型效果。 |
SPSSAU【机器学习】模块提供多种算法，无需编程即可完成分析，如下图：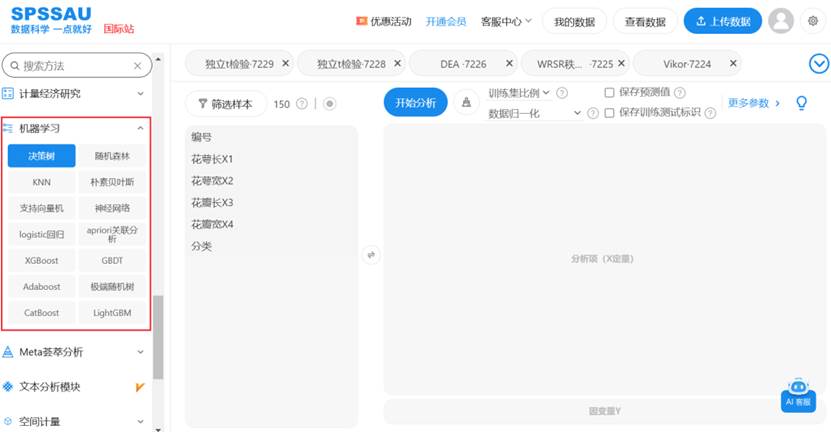
点击下方链接跳转至相应方法帮助手册：
- 决策树
- 随机森林
- KNN
- 朴素贝叶斯
- 支持向量机
- 神经网络
- logistic回归
- apriori关联分析
- Xgboost模型
- GBDT模型
- Adaboost模型
- 极端随机数
- CatBoost模型
- LightGBM模型
3、预测模型
数学建模预测模型是一种利用数学模型和统计方法来预测未来可能发生的结果的模型。它通常基于历史数据和已知信息，通过建立数学模型来分析问题，并预测未来的发展趋势。预测类常见的方法有时间序列类预测、回归分析进行预测、机器学习进行预测等。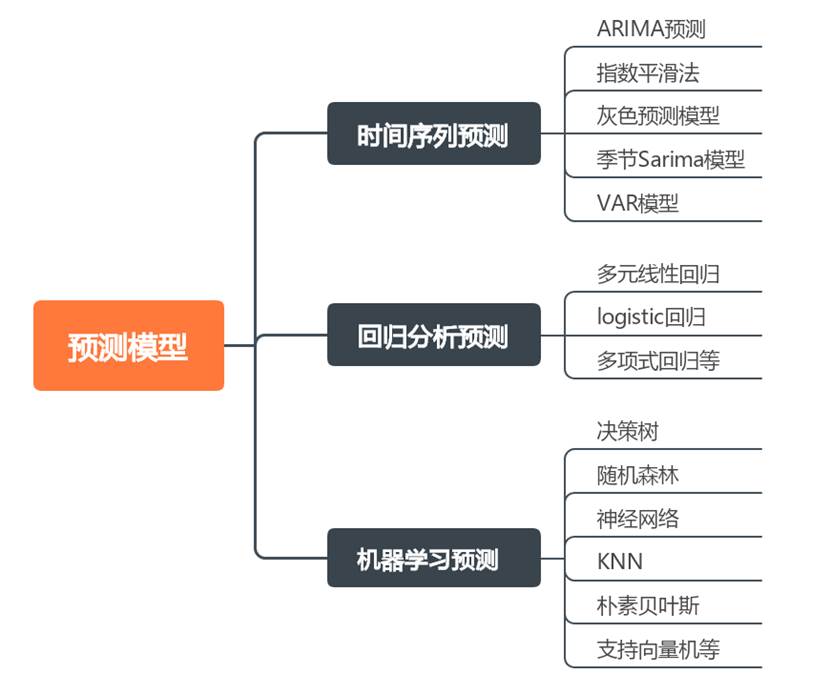
（1）时间序列预测
时间序列数据预测是利用按时间顺序排列的历史数据，分析其变化规律并推测未来发展趋势的方法，广泛应用于金融、气象、经济等领域。比较常用的时间序列数据预测方法有ARIMA预测、指数平滑法、灰色预测模型、VAR模型、季节Sarima模型，说明如下：
| 方法 | 说明 |
| ARIMA预测 | 自回归积分滑动平均模型，适用于非平稳时间序列数据的预测。 |
| 指数平滑法 | 简单的时间序列预测方法，通过指数衰减历史数据的权重来预测未来值。 |
| 灰色预测模型 | 基于灰色系统理论的预测方法，通过构建灰色模型GM(1,1)来预测时间序列数据。 |
| VAR模型 | 向量自回归模型，用于分析多个时间序列变量之间的动态关系。 |
| 季节Sarima模型 | 季节性自回归积分滑动平均模型，适用于具有季节性的时间序列数据的预测。 |
点击下方链接跳转至相应方法帮助手册：
- ARIMA预测
- 指数平滑法
- 灰色预测模型
- VAR模型
- 季节Sarima模型分析
（2）回归分析预测
回归分析是一种常用的统计方法，用于建立变量间的关系模型，并通过该模型对未知数据进行预测。常用方法如多元线性回归、logistic回归、多项式回归等，说明如下：
| 方法 | 说明 |
| 多元线性回归 | 当自变量与因变量之间存在线性关系时，适用于连续性因变量，用于预测数值型数据 |
| Logistic回归 | 当因变量为定类数据时，用于预测概率 |
| 多项式回归 | 当自变量与因变量存在非线性关系时，用于预测非线性关系的数值型数据 |
点击下方链接跳转至相应方法帮助手册：
- 多元线性回归
- Logistic回归
- 多项式回归（非线性回归）
（3）机器学习预测
机器学习用于从数据中学习模式和规律，并利用这些知识进行预测。通过训练算法来自动发现数据中的模式，并根据这些模式进行未知样本的预测。常用方法及说明如下：
| 方法名称 | 描述 |
| 决策树 | 基于树结构划分数据，通过特征选择实现分类或回归预测。 |
| 随机森林 | 集成多棵决策树，通过投票或平均结果提升预测鲁棒性。 |
| KNN | 根据邻近样本的多数类别或均值进行预测，适用于局部模式识别。 |
| 朴素贝叶斯 | 基于贝叶斯定理与特征独立性假设，计算概率实现分类。 |
| 支持向量机 | 通过寻找最优超平面最大化分类间隔，适用于高维数据。 |
| 神经网络 | 模拟人脑神经元连接，通过多层非线性变换学习复杂模式。 |
| logistic回归 | 利用Sigmoid函数将线性输出映射为概率，解决二分类问题。 |
| apriori关联分析 | 挖掘数据项集间的关联规则，用于发现频繁共现模式（如购物篮分析）。 |
| XGBoost | 优化梯度提升树，引入正则化与并行计算，提升预测精度与效率。 |
| GBDT | 迭代训练弱决策树，通过梯度下降逐步修正残差，实现强预测模型。 |
| Adaboost | 动态调整样本权重，组合弱分类器为强分类器，侧重纠正错误样本。 |
| 极端随机树 | 随机选择特征与分裂点构建决策树，增强模型泛化能力。 |
| CatBoost | 自动处理类别特征，通过排序提升减少过拟合，优化梯度提升效果。 |
| LightGBM | 基于直方图的梯度提升框架，采用Leaf-wise生长策略加速训练，适合大规模数据。 |
点击下方链接跳转至相应方法帮助手册：
- 决策树
- 随机森林
- KNN
- 朴素贝叶斯
- 支持向量机
- 神经网络
- logistic回归
- apriori关联分析
- Xgboost模型
- GBDT模型
- Adaboost模型
- 极端随机数
- CatBoost模型
- LightGBM模型
有关预测模型的总结可查看往期这篇文章，做过完整介绍：
常用预测类数据分析方法分类汇总
四、模型评估
在模型构建与分析过程中，模型评价是不可或缺的环节。选用恰当的评价指标，有助于客观衡量模型性能，并指导后续的优化与改进。不过，评价指标的选择需结合具体模型和应用场景而定。
1、回归模型评价指标
回归模型常用的评价指标可分为以下三大类：
- 第1类：回归模型拟合优度的评价指标，包括R方与调整后R方值；
- 第2类：回归模型拟合值与真实值的差异程度的评价指标，常用的包括MSE、RMSE、MAE、MAPE；
- 第3类：极大似然法的估计准则，包括AIC值和BIC值。
指标说明如下：
| 指标名称 | 说明 |
| R方 | 衡量模型拟合度，表示自变量对因变量变化的解释比例。范围 [0, 1]，越接近1越好。 |
| 调整后R方 | 对R方进行修正，引入了模型复杂度惩罚项（自变量个数p）。 |
| MSE | 均方误差，预测值与真实值之差的平方的平均值。 |
| RMSE | 均方根误差，MSE的平方根。 |
| MAE | 平均绝对误差，预测值与真实值之差的绝对值的平均值。 |
| MAPE | 平均绝对百分比误差，将每个误差表示为百分比的形式。 |
| AIC | 赤池信息准则，衡量统计模型的相对拟合优度，引入了模型复杂度的惩罚。 |
| BIC | 贝叶斯信息准则，与AIC类似，但对模型复杂度的惩罚更重（尤其当样本量n较大时）。 |
SPSSAU在进行分析时，会自动输出相应的评价指标，如线性回归输出部分结果如下:
【提示】：综合使用不要只依赖一个指标。应结合RMSE/MAE看误差大小，结合R²看解释度，再结合AIC/BIC来权衡复杂度和拟合效果。
2、分类模型评价指标
分类模型常用评价指标说明如下：
| 指标名称 | 说明 |
| 准确率 (Accuracy) | 分类正确的样本数占总样本数的比例 |
| 精确率 (Precision) | 正确预测为正类的样本数占预测为正类的样本总数的比例 |
| 召回率 (Recall) | 正确预测为正类的样本数占实际正类样本总数的比例 |
| F1-score | 精确率和召回率的调和平均数 |
| ROC曲线 | 接收者操作特征曲线，展示不同阈值下真正率（TPR）和假正率（FPR）的关系 |
| AUC值 | ROC曲线下面积，值越大表示模型分类性能越好 |
【提示】：选择指标时需根据具体业务需求和对不同类型错误的容忍度来决定。例如，在医疗诊断中，可能更关注召回率以减少漏诊；而在垃圾邮件检测中，可能更关注精确率以减少误判。SPSSAU决策树模型输出部分评价指标结果如下：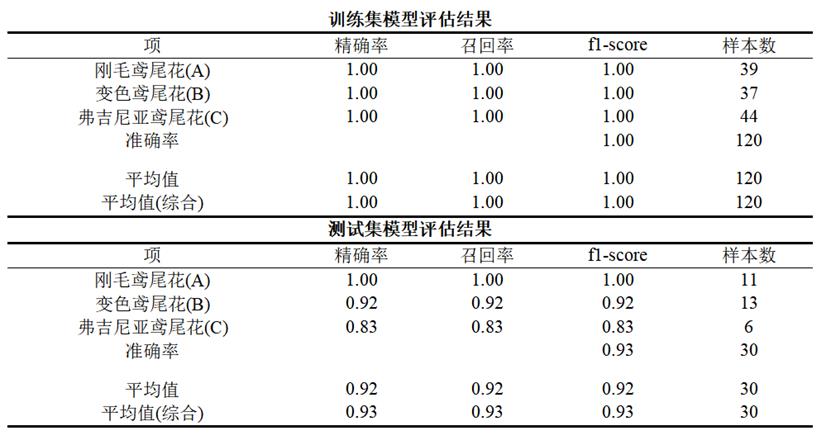
以上就是数学建模竞赛可能涉及到的大部分模型以及方法，使用SPSSAU系统都可以快速完成，即便是不会建模的小白，也可以冲刺一下奖项哦~今天的干货有点长，看到这里的同学是真爱粉无疑了。预祝看到这里的同学都能拿国一！！！