题目：快乐数

快乐数

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

---

经典的循环或相遇的问题，对于此类问题采用Floyd判圈算法

class Solution {
public:int lzgnum(int n){   //n=19int sum = 0;while (n){int t = n % 10;sum += t * t;n /= 10;}return sum;}bool isHappy(int n) {int slow = n;int fast = lzgnum(n);while (slow != fast){slow = lzgnum(slow);fast = lzgnum(lzgnum(fast));}return slow == 1;}
};

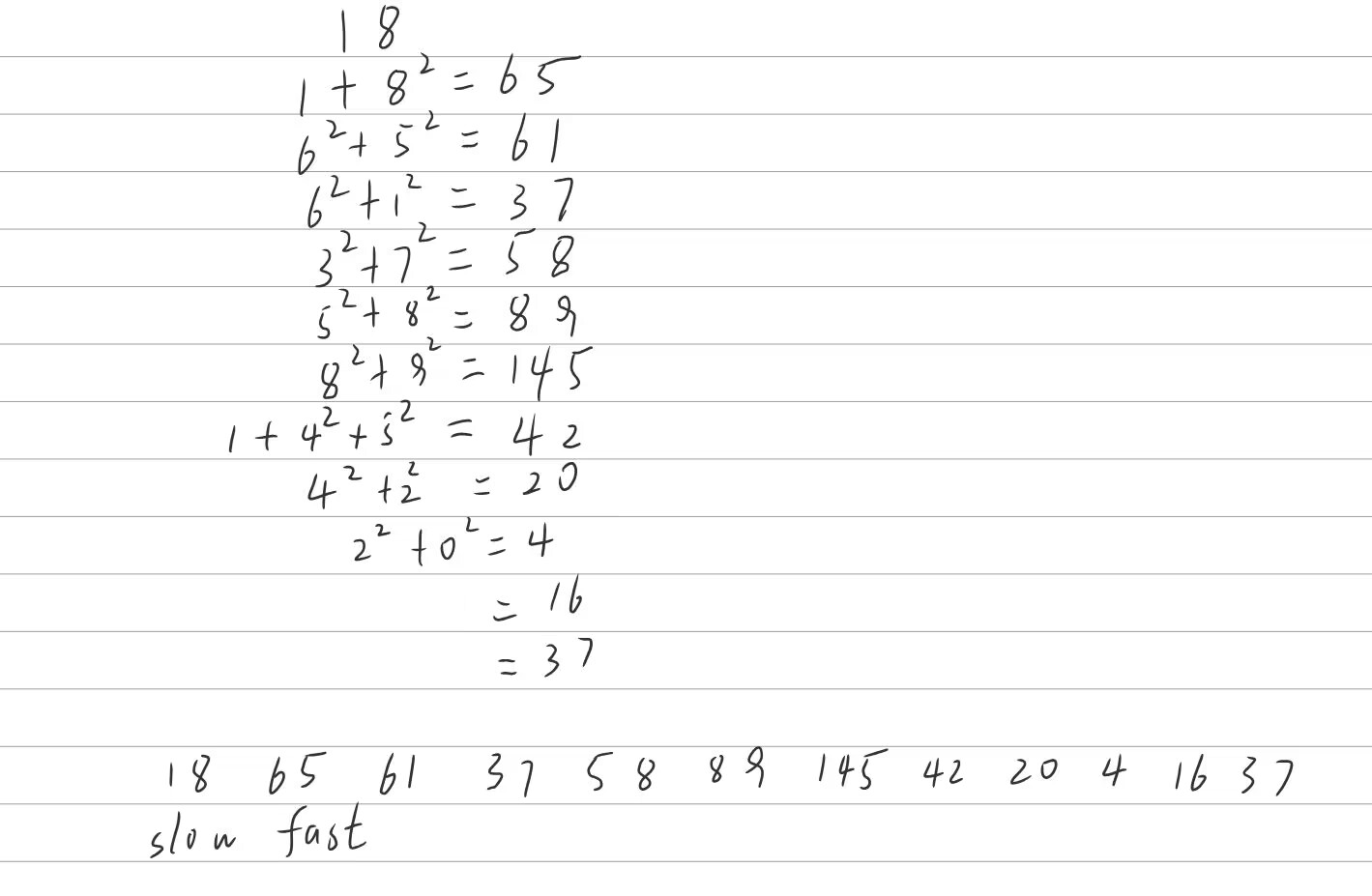
什么是采用Floyd判圈算法？

​Floyd判圈算法（Floyd's Cycle-Finding Algorithm）​，也被形象地称为龟兔赛跑算法（Tortoise and Hare Algorithm）​，是一种用于检测序列或链表中是否存在环（循环）的经典算法。它由计算机科学家罗伯特·弗洛伊德（Robert W. Floyd）提出。

它的核心思想非常简单且巧妙：使用两个指针以不同的速度遍历序列，如果序列中存在环，那么这两个指针必定会在环内的某一点相遇。

算法思想与比喻

让我们用一个生动的比喻来理解它：

• 场景​：一条跑道，可能是一条直道（无环），也可能是一个环形跑道（有环）。
• ​角色​：
  • ​乌龟（Tortoise）​​：一个慢指针，每次前进一步。
  • 兔子（Hare）​​：一个快指针，每次前进两步。
• ​推理​：
  1. 如果跑道是直的（无环）​​：兔子会永远跑在乌龟前面，它们永远不会再次相遇。
  2. 如果跑道是环形的（有环）​​：尽管兔子跑得快，先进入了环，但乌龟最终也会进入环。进入环后，兔子就在环里绕着圈跑。​每经过一个时间单位，兔子就会比乌龟多跑一圈的距离。因此，无论初始位置如何，兔子最终一定会从后面追上乌龟并相遇。

这个比喻完美地解释了Floyd算法的基本原理。

算法步骤

将该思想应用到链表或数组等数据结构中，步骤如下：

1. ​初始化​：创建两个指针（或索引），通常命名为 slow（乌龟）和 fast（兔子）。将它们都置于序列的起始点（或者根据问题要求，置于指定的初始位置）。
2. 移动​：在每一步迭代中：
   • 慢指针 slow向前移动 ​1​ 个节点（或单位）。
   • 快指针 fast向前移动 ​2​ 个节点（或单位）。
3. ​检查​：
   • 如果快指针 fast遇到了序列的终点（如 nullptr，数组越界等）​​：说明序列无环，算法结束。
   • ​如果快指针 fast和慢指针 slow指向了同一个元素​：说明序列中存在环，算法结束。
4. 重复​：重复步骤2和3，直到满足上述任一检查条件。