当前位置：首页 > news >正文

[数据结构] 优先级队列(堆)

news 2025/9/13 5:24:34

1. 优先级队列

1.1 概念

2. 优先级队列的实现

2.1 堆的概念

2.2 堆的存储

2.3 堆的创建

2.3.1 堆的向下调整

2.4 堆的插入与删除(向上调整）

3. PriorityQueue类

3.1 PriorityQueue类的性质

3.2 PriorityQueue类的构造方法

3.3 PriorityQueue类常用的方法

3.4 练习题

4. 堆的应用

4.1 堆排序

4.2 Top-k问题

1. 优先级队列

1.1 概念

队列是一种先进先出的数据结构，但是在操作的数据具有优先级的情况下，就需要根据优先级来决定出队列。比如说：在飞机排队登机时，vip用户优先级高于普通用户，可以先进入飞机。

此时就引出了优先级队列，包含两个基本操作，返回最高优先级元素和添加元素。

2. 优先级队列的实现

在Java中优先级队列对应priorityQueue类，底层实现使用了堆这种数据结构，堆是在完全二叉树的基础上进行了改造。

2.1 堆的概念

将一个集合中的元素按照完全二叉树的顺序存储到一维数组中，当满足根节点最大，其子树根节点大于其子节点的堆叫做大根堆，反之则叫做小跟堆。

堆中的某的节点的值小于等于或者大于等于其父节点的值。
堆是一棵完全二叉树。

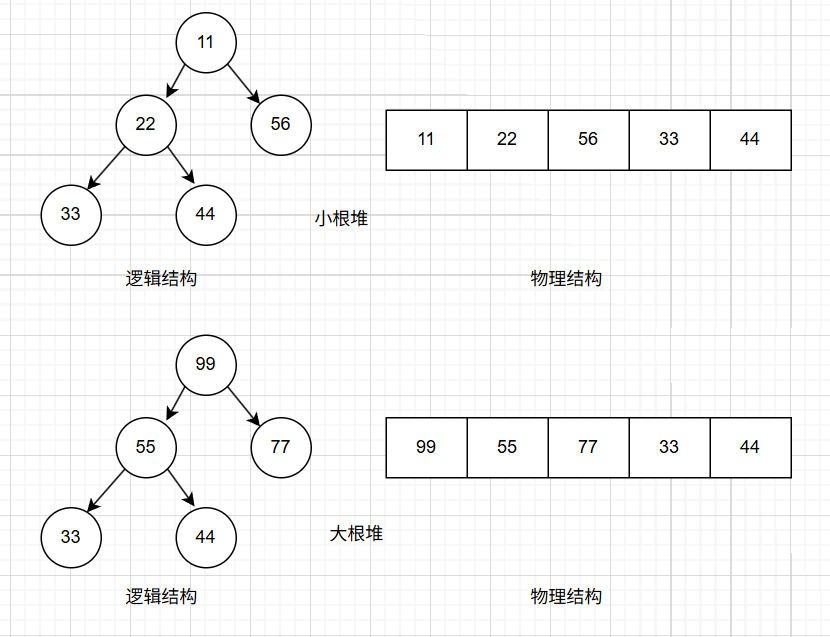
2.2 堆的存储

堆采用的顺序存储方式，将元素存储到数组中，假设第i个节点：

若i为0 ，则表示为根节点，否则 i 的双亲节点为（i - 1) / 2 。
若 2 * i +1 <= n，则节点 i 的左结点为2 * i + 1. 否则没有左孩子。
若2* i + 2 <= n , 则节点 i 的右节点为2 * i + 2 . 否则没有右孩子。

2.3 堆的创建

2.3.1 堆的向下调整

例如一个集合{27,15,19,18,28,34,65,49,25,37 }，将其创建成一个堆：

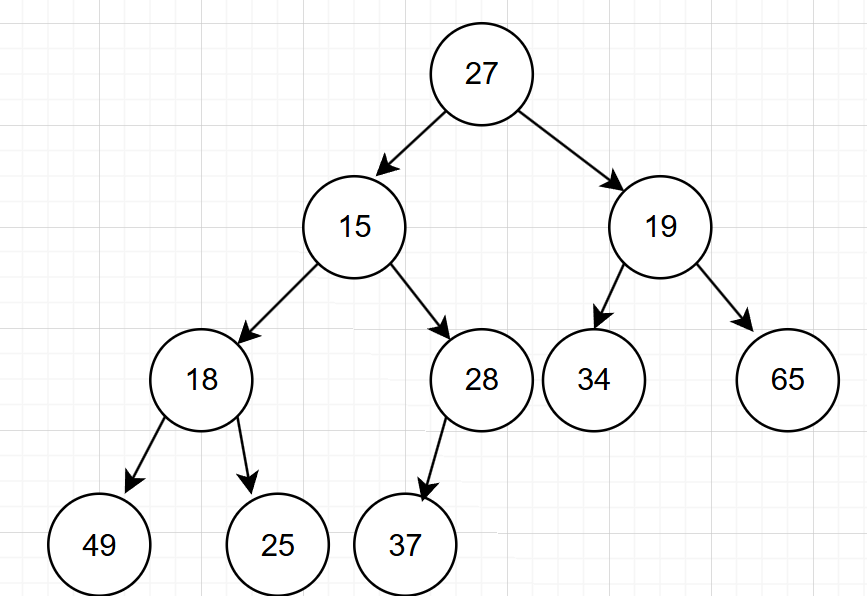
上面该集合的堆形态，如何将其转化为一个大根堆呢？

向下调整：

这里我们可以先调整子树，当所有子树都为大根堆时，该树整体也为大根堆。

这里我们可以先调整只有两层的子树，如何调整？

可以先获取子树的根节点，如果有左孩子和右孩子，将根节点与左右孩子节点的最大值比较，来判断是否交换位置，如果只有左孩子，只用跟左孩子比较。如果没有孩子，则不用再进行交换。

我们从最后一棵两层子树开始向下调整，最后一棵子树的根节点为（n - 1- 1) /2 n为该堆的元素数量。当根节点比较到整棵树的根节点时候停止。

代码如下：

    //创建大根堆(利用向下调整的思维)//时间复杂度：O(N)public void createBigHeap() {for (int parent = (userSize -1-1)/2; parent >= 0; parent--) {siftDown(parent,userSize);}}//向下调整public void siftDown(int p, int userSize) {int child = 2*p + 1;while(child < userSize) {//判断是否存在右节点，存在的话再判断节点的值是否大于左节点if(child+1 < userSize && elem[child] < elem[child+1]) {child = child+1;}//此时child是左右节点中的最大值的下标if(elem[child] > elem[p]) {swap(child,p);p = child;child = 2 * p +1;}else {break;}}}

上面是将一个普通堆转换成一个大根堆的过程，采用了向下调整的思维。

利用向下调整创建的大根堆的时间复杂度为O(N)

2.4 堆的插入与删除(向上调整）

堆的插入是在堆的最后一个位置插入元素，然后利用向上调整，来保持大根堆的形态。

时间复杂度为O(logn)。

如果以向上调整的方式创建堆，时间复杂度为n*logn。

代码如下：

    //插入元素(将元素放到最后一个位置）public void offer(int val) {if(isFull()) {elem = Arrays.copyOf(elem,2*elem.length);}//进行向上调整elem[userSize] = val;siftUp(userSize);userSize++;}//判断栈是否满了public boolean isFull() {return userSize == elem.length;}//向上调整//利用向上调整创建的大根堆时间复杂度为：O(N*logN)public void siftUp(int child) {int p = (child - 1) / 2;while(p >= 0) {if(elem[p] < elem[child]) {swap(p,child);child = p;p = (child - 1) / 2;}else {break;}}}

堆的删除是删除的头节点，原理是将头节点和最后元素交换位置，然后利用向下调整为大根堆。

代码如下：

    //删除元素(从根节点开始删除)//原理：将根节点元素与最后一个元素交换位置public int poll() {if(isEmpty()) {return -1;}int val = elem[0];swap(0,userSize-1);userSize--;siftDown(0,userSize);return val;}//判断栈是否为空public boolean isEmpty() {return userSize == 0;}

3. PriorityQueue类

3.1 PriorityQueue类的性质

Java的集合框架中提供了PriorityQueue和PriorityBlockingQueue两种优先级队列。

PriorityQueue是线程不安全的，PriorityBlockingQueue是线程安全的。

下面主要介绍下PriorityQueue类:

该类的底层使用的是堆结构。
该类所在的包是java.util.PriorityQueue包里面。
PriorityQueue里面放置的元素应该是可以比较的类型，如果不能比较则会抛出ClassCastException异常
不能往里面插入null，否则会抛出NullPointerException异常。
当该队列满了，会自动进行扩容。
插入和删除元素的时间复杂度为n * logn。
默认创建的堆是小根堆。

3.2 PriorityQueue类的构造方法

下面是该类的三种主要构造方法：

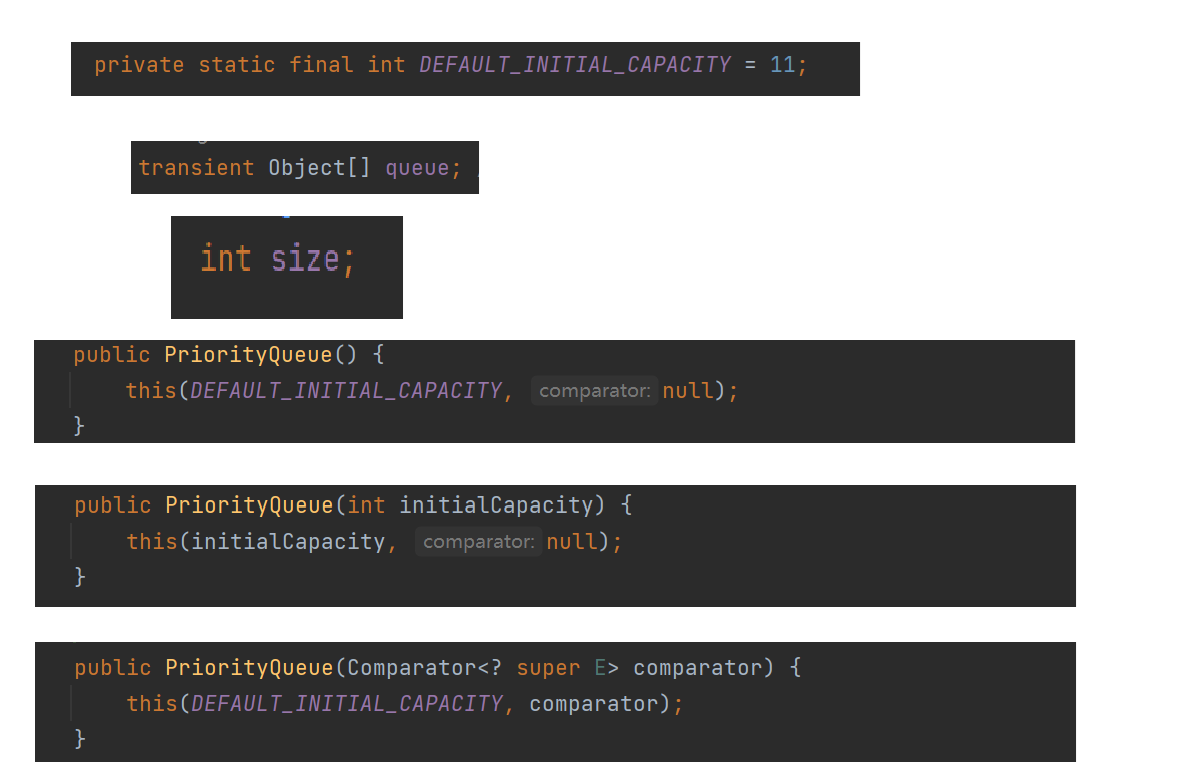
第一个构造方法：没有参数，Java自己提供了一个大小为11的数组储存数据，没有构造器。

第二个构造方法：传入的参数为创建数组的大小，没有构造器。

第三个构造方法：传入的参数是一个构造器。

我们重点讲解下第三个构造方法：

当我们创建一个堆的时候，Java默认创建的是小根堆，为什么呢？我们可以看下源码：

下面是我们默认使用offer方法创建的小根堆：

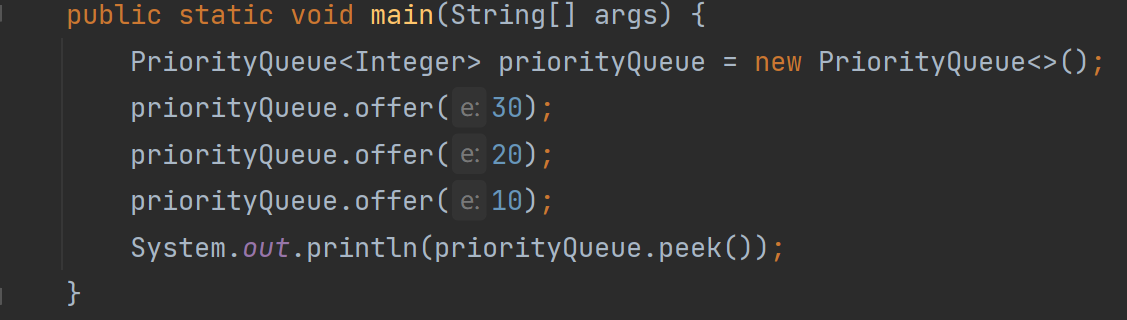
下面是offer的源码:

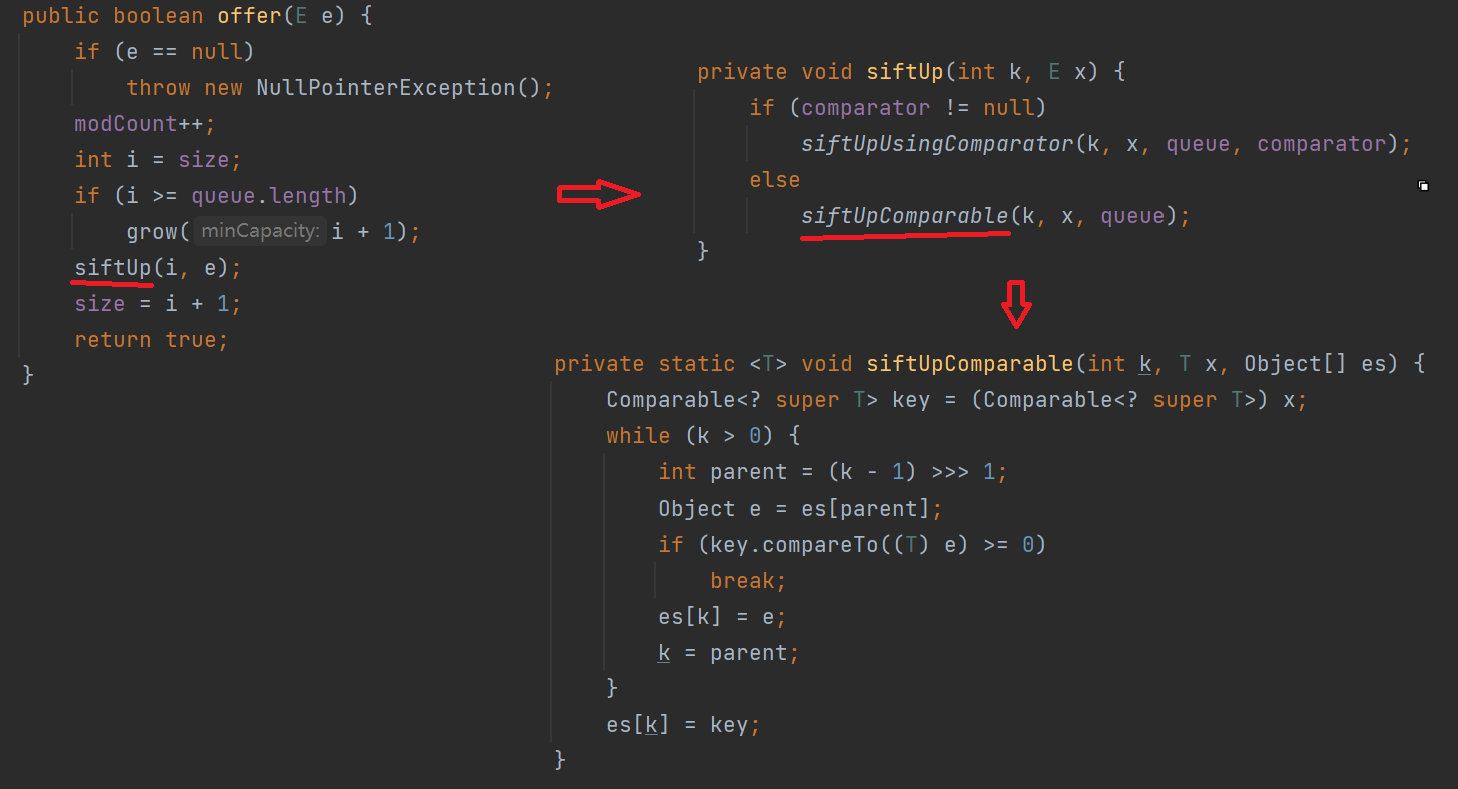
根据上面的内容，我们可以发现offer方法先检查传入的数据是否有效，有效的话就调用siftUp方法，这个方法检查一下是否有构造器，没有构造器就调用siftUpComparable方法，该方法是向上调整的方法（前面讲过）这个方法会调用compareTo接口来比较插入进来的数跟头节点的数谁大，用插入进来的数 - 头节点的数大于等于0的话不会交换位置，但是小于0的话会交换位置，换成小根堆。

那我们如何让他变成大根堆呢？

我们可以创造一个构造器，调用第三个构造方法，就实现大根堆的转换，代码如下：

class ImpMaxComparator implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o2.compareTo(o1);}
}
public class Test {public static void main(String[] args) {ImpMaxComparator impMaxComparator = new ImpMaxComparator();PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(impMaxComparator);priorityQueue.offer(30);priorityQueue.offer(20);priorityQueue.offer(10);System.out.println(priorityQueue.peek());}
}

3.3 PriorityQueue类常用的方法

在priorityQueue类里面如果堆满时要添加元素，此时系统会自动扩容，当堆的容量小于64时，2倍扩容，当容量大于等于64时，1.5倍扩容。

3.4 练习题

最小的K个数

解题思路：这里我们创建了一个比较器，将前k个数排列成大根堆，然后将数组后面的数依次跟头节点比较，如果小于头节点的值，则说明头节点不是前k个最小的数，将头节点替换成这个数，依次类推，最后堆里面就是前k个最小的数。

代码实现：

class ImpMaxComparator implements Comparator<Integer> {public int compare(Integer o1, Integer o2) {return o2.compareTo(o1);}
}
class Solution {public int[] smallestK(int[] arr, int k) {int[] array = new int[k];if(arr == null || k < 1) {return array;}ImpMaxComparator impMaxComparator = new ImpMaxComparator();PriorityQueue<Integer> PriorityQueue = new PriorityQueue<>(impMaxComparator);//创建前k个数的小根堆for(int i = 0; i < k; i++) {PriorityQueue.offer(arr[i]);}//将剩下的数据跟头节点比较for(int i = k; i < arr.length; i++) {int a = PriorityQueue.peek();if(a > arr[i]) {PriorityQueue.poll();PriorityQueue.offer(arr[i]);}}//将前k个最小数放到数组里面for(int i = 0; i < k; i++) {array[i] = PriorityQueue.poll();}return array;}
}

4. 堆的应用

4.1 堆排序

将堆按照从小到大的顺序排列，这里需要建大堆，代码如下：

    //堆排序(从小到大排)public void heapSort() {int a = userSize - 1;while(a > 0) {swap(0, a);siftDown(0,a);a--;}//向下调整public void siftDown(int p, int userSize) {int child = 2*p + 1;while(child < userSize) {//判断是否存在右节点，存在的话再判断节点的值是否大于左节点if(child+1 < userSize && elem[child] < elem[child+1]) {child = child+1;}//此时child是左右节点中的最大值的下标if(elem[child] > elem[p]) {swap(child,p);p = child;child = 2 * p +1;}else {break;}}}

4.2 Top-k问题

TOP-K问题：即求数据集合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大

解题思路：

第一步：将前K个元素组成的堆进行排序，求前K个最大元素，排序成小根堆，求前K个最小元素，排序成大根堆。

第二步：这里以求前K个最大元素为例，将剩下的N-K个元素依次与根节点比较，比根节点大的，说明根节点不是前K个最大元素，交换位置，再重新排序成小根堆。

代码实现：

这里是前k个最大元素为例实现的代码：

    public static int[] smallest(int[] arr, int k) {int[] array = new int[k];if(arr == null || k < 1) {return array;}PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();for (int i = 0; i < k; i++) {priorityQueue.offer(arr[i]);}for (int i = k; i < arr.length; i++) {int a = priorityQueue.peek();if(a < arr[i]) {priorityQueue.poll();priorityQueue.offer(arr[i]);}}for (int i = 0; i < k; i++) {array[i] = priorityQueue.poll();}return array;}