硅基计划4.0 算法 归并排序
硅基计划4.0 算法 归并排序

文章目录
- 硅基计划4.0 算法 归并排序
- 一、排序数组
- 二、寻找数组中的逆序对个数——hard
- 三、计算右侧小于当前元素的个数——hard
- 四、翻转对——hard
一、排序数组
题目链接
这题我们之前是用快排解决的,这次我们要使用归并排序解决
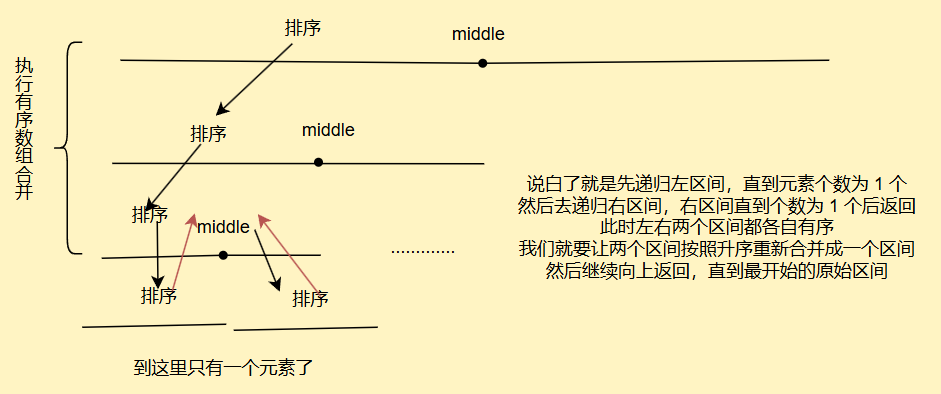
说白了就是选取一个中间点middle,将数组划分成两个区域
递归去排序左边的区间,直到元素个数为1个,返回
递归去排序右边的区间,直到元素个数为1个,返回
按照合并两个有序数组操作,将两个区间合并成一个区间,重复操作,直到最原始的区间
如果还没有做过合并两个有序数组,我这里放出题目链接,利用双指针完成序列合并
有序序列合并题目链接
合并两个有序数组数组代码
//合并两个有序数组数组代码
class Solution {public void merge(int[] nums1, int m, int[] nums2, int n) {int pos = 0;//标记排序后数组下标int current1 = 0;//第一个数组指针int current2 = 0;//第二个数组指针int [] ret = new int[m+n];while(current1 < m && current2 < n){if(nums1[current1] <= nums2[current2]){ret[pos] = nums1[current1];current1++;}else{ret[pos] = nums2[current2];current2++;}pos++;}//处理没排完序的数组while(current1 < m){ret[pos] = nums1[current1];current1++;pos++;}while(current2 < n){ret[pos] = nums2[current2];current2++;pos++;}for(int i = 0;i < nums1.length;i++){nums1[i] = ret[i];}}
}
//题目代码
class Solution {int [] temp;//辅助数组,用于合并区间使用public int[] sortArray(int[] nums) {temp = new int[nums.length];sortArrayPlus(nums,0,nums.length-1);return nums;}private void sortArrayPlus(int [] nums,int left,int right){if(left >= right){return;}int middle = (left+right)/2;sortArrayPlus(nums,left,middle);sortArrayPlus(nums,middle+1,right);//合并有序数组int current1 = left;int current2 = middle+1;int pos = 0;while(current1 <= middle && current2 <= right){if(nums[current1] <= nums[current2]){temp[pos] = nums[current1];current1++;}else{temp[pos] = nums[current2];current2++;}pos++;}//处理剩下元素while(current1 <= middle){temp[pos] = nums[current1];current1++;pos++;}while(current2 <= right){temp[pos] = nums[current2];current2++;pos++;}//将结果重新放入数组中for(int i = left;i <= right;i++){nums[i] = temp[i-left];}}
}
二、寻找数组中的逆序对个数——hard
题目链接
这题可以和我们上一题一样的思想,我们将数组划分为两个区域
在左区间内选出a个逆序对,在右边区间内选出b个逆序对,然后在左右区间内各选一个数选出c个逆序对,然后求和
但是,我们这一题可以更加优化一点,我们利用归并排序的思想,准确来说,是利用归并排序,帮我们快速找到逆序对
首先,我们上一题的归并排序是可以把左右两个区间变成一个有序的区间,默认是升序
我们不是要寻找逆序对吗,我们可以这样,参考我们有序序列合并的双指针
左边区间的起点我们定义一个current1指针,右区间起点我们定义一个current2指针
我们的目标就是找到current2所指的数之前有多少个数比current2所指的数大
如果我们nums[current1] <= nums[current2],说明我们在左边并没有找到比nums[current2]大的数,此时我们current1++,往后走
如果我们nums[current1] > nums[current2],说明我们第一次找到了比nums[current2]大的数
但是不要忘记,我们数组是升序排序的,左边小右边大,那这也就说明nums[current1]右边的数也是符合要求的,因此我们current1不需要往右继续走了
此时current1和middle区间内都是符合要求的值,因此我们统计这个区间内的元素个数
之后,区间个数统计完了,我们的current2要向右走,看看nums[current1]是否还是比nums[current2]值大
class Solution {int [] tmp;public int reversePairs(int[] record) {int length = record.length;tmp = new int[length];return reversePairsPlus(record,0,length-1);}private int reversePairsPlus(int [] nums,int left,int right){if(left >= right){return 0;}int count = 0;int middle = (left+right)/2;count += reversePairsPlus(nums,left,middle);count += reversePairsPlus(nums,middle+1,right);int current1 = left;int current2 = middle+1;int pos = 0;while(current1 <= middle && current2 <= right){if(nums[current1] <= nums[current2]){tmp[pos] = nums[current1];current1++;}else{count += middle-current1+1;tmp[pos] = nums[current2];current2++;}pos++;}while(current1 <= middle){tmp[pos] = nums[current1];current1++;pos++;}while(current2 <= right){tmp[pos] = nums[current2];current2++;pos++;}for(int i = left;i<=right;i++){nums[i] = tmp[i-left];}return count;}
}
那我们有序序列合并就一定要是升序吗,并不是,我们也可以使用降序
如果我们还采用刚刚的比较方法,寻找之前的数比它大
会存在重复计算,请看
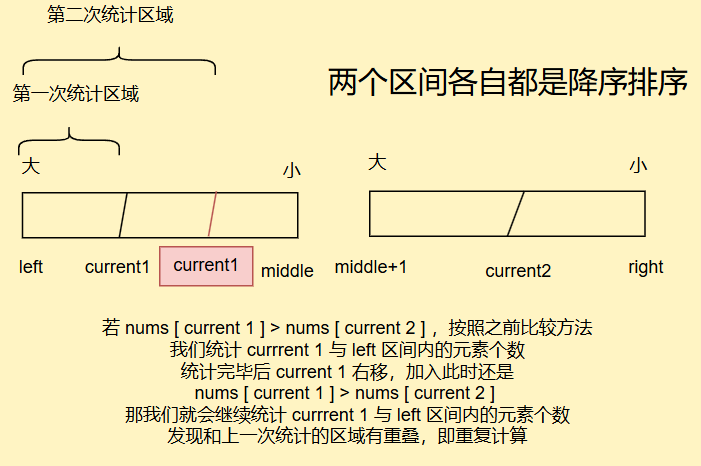
因此我们要采用其他的计数方法,既然统计之前的数行不通,那我们就去统计之后的数,即
找到current2所指的数之后有多少个数比current2所指的数大
此时如果nums[current1] > nums[current2],由于是降序排序
此时nums[current2]右边的数都比nums[current2]小,因此从current2到right区间内的数都符合要求,因此统计区间内的元素个数
统计完毕后,current1向后走,看看下一个数是否还是比nums[current2]大
如果nums[current1] <= nums[current2],说明左边还没有出现比右边大的数
由于是降序,因此current2左边的数肯定不符合要求,因此current2向后走
class Solution {int [] tmp;public int reversePairs(int[] record) {int length = record.length;tmp = new int[length];return reversePairsPlus(record,0,length-1);}private int reversePairsPlus(int [] nums,int left,int right){if(left >= right){return 0;}int count = 0;int middle = (left+right)/2;count += reversePairsPlus(nums,left,middle);count += reversePairsPlus(nums,middle+1,right);int current1 = left;int current2 = middle+1;int pos = 0;while(current1 <= middle && current2 <= right){if(nums[current1] <= nums[current2]){tmp[pos] = nums[current2];current2++;}else{count += right-current2+1;tmp[pos] = nums[current1];current1++;}pos++;}while(current1 <= middle){tmp[pos] = nums[current1];current1++;pos++;}while(current2 <= right){tmp[pos] = nums[current2];current2++;pos++;}for(int i = left;i<=right;i++){nums[i] = tmp[i-left];}return count;}
}
三、计算右侧小于当前元素的个数——hard
题目链接
这道题其实和我们上一题的思想差不多,不同的就是我们要统计每个下标右边区域中逆序对的个数
因此我们需要一个结果数组,去记录每个下标右侧范围内的逆序对个数
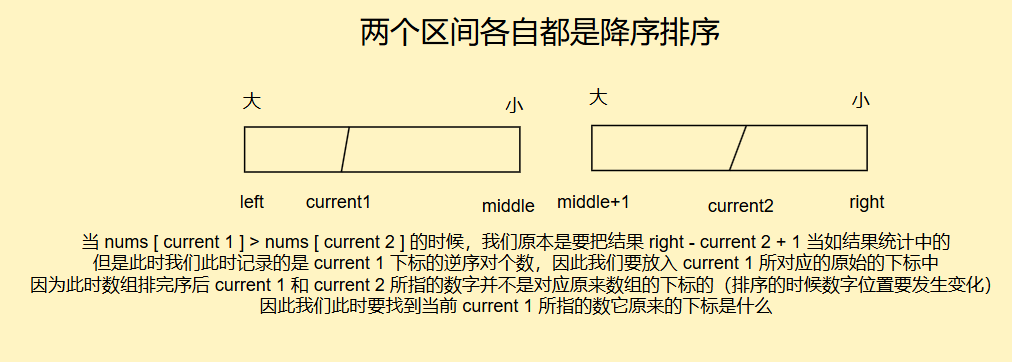
好,现在我们如何直到这个数的原始下标呢?
你肯定想到了哈希表,但是使用哈希表万一出现重复元素会很棘手
因此我们使用一个index数组去记录原始下标的值,让数组中的每个值和index数组中每个值绑定在一起,当原数组元素变到时,index的值也对应变动
原数组:nums [1,6,4,2,5]
index数组: [0,1,2,3,4]
数组分成两半后再排序
原数组:nums [6,1,5,2,4]
index数组: [1,0,4,3,2]
可以看到,当我原数组排完序后,index数组中一起变化,当我要找原数组中的值的原始下标时,直接去index数组中找就好
比如找6的原始下标,此时6在原数组中下标是0,因此index[0] == 1得到的就是6的原始下标
还有,我们在归并排序数组时不是使用了临时数组吗,那我们在移动下标的时候,也要用到临时数组
class Solution {int [] ret;//结果数组int [] index;//下标数组int [] tmpNums;//归并排序的数值临时数组int [] tmpIndex;//归并排序的下标临时数组public List<Integer> countSmaller(int[] nums) {int length = nums.length;index = new int[length];for(int i = 0;i < length;i++){index[i] = i;}ret = new int[length];tmpIndex = new int[length];tmpNums = new int[length];countSmallerPlus(nums,0,length-1);List<Integer> list = new ArrayList<>();for(int x : ret){list.add(x);}return list;}private void countSmallerPlus(int [] nums,int left,int right){if(left >= right){return;}int middle = (left+right)/2;countSmallerPlus(nums,left,middle);countSmallerPlus(nums,middle+1,right);//处理一左一右情况int current1 = left;int current2 = middle+1;int pos = 0;while(current1 <= middle && current2 <= right){if(nums[current1] > nums[current2]){ret[index[current1]] += right-current2+1;tmpNums[pos] = nums[current1];tmpIndex[pos] = index[current1];current1++;}else{tmpNums[pos] = nums[current2];tmpIndex[pos] = index[current2];current2++;}pos++;}//处理剩下元素while(current1 <= middle){tmpNums[pos] = nums[current1];tmpIndex[pos] = index[current1];current1++;pos++;}while(current2 <= right){tmpNums[pos] = nums[current2];tmpIndex[pos] = index[current2];current2++;pos++;}//结果放入原数组中for(int i = left;i <= right;i++){nums[i] = tmpNums[i-left];index[i] = tmpIndex[i-left];}}
}
四、翻转对——hard
题目链接
这题和寻找逆序对个数很相似,但是不同的就在于,我们找逆序对时考虑的只是一倍关系上的大小比较
而我们这一题求的是两倍关系的大小比较,而在原来的固定排序下是一倍的关系比较,去排序数组 是可以的
但是现在是两倍的关系比较,因此不能和求逆序对一样,在归并排序的时候求个数
因此我们就需要在归并排序之前就先把个数求好
哦对了,不要忘记在比较的时候,要使用long类型比较,因为会出现很大的数
先来个降序版本
class Solution {int [] tmp;public int reversePairs(int[] record) {int length = record.length;tmp = new int[length];return reversePairsPlus(record,0,length-1);}private int reversePairsPlus(int [] nums,int left,int right){if(left >= right){return 0;}int count = 0;int middle = (left+right)/2;count += reversePairsPlus(nums,left,middle);count += reversePairsPlus(nums,middle+1,right);int current1 = left;int current2 = middle+1;//先计算反转对,固定current1,使用long防止溢出while(current1 <= middle){while(current2 <= right && (long)nums[current2]*2 >= (long)nums[current1]){current2++;}if(current2 > right){break;}count += right-current2+1;current1++;}//再来合并有序数组int pos = 0;current1 = left;current2 = middle+1;while(current1 <= middle && current2 <= right){if(nums[current1] > nums[current2]){tmp[pos] = nums[current1];current1++;}else{tmp[pos] = nums[current2];current2++;}pos++;}while(current1 <= middle){tmp[pos] = nums[current1];current1++;pos++;}while(current2 <= right){tmp[pos] = nums[current2];current2++;pos++;}for(int i = left;i<=right;i++){nums[i] = tmp[i-left];}return count;}
}
补充一下,为什么在求翻转对的时候,循环式这么写的
//先计算反转对,固定current1,使用long防止溢出while(current1 <= middle){while(current2 <= right && (long)nums[current2]*2 >= (long)nums[current1]){current2++;}if(current2 > right){break;}count += right-current2+1;current1++;}
首先,我们这么做的目的就是先固定current1,然后让current2往后遍历
直到遇见nums[current1] > nums[current2]*2为止,此时这个循环while(current2 <= right && (long)nums[current2]*2 >= (long)nums[current1])才出来
此时我们统计区间长度即可,但是为什么if(current2 > right){break;}呢?
这是因为由于数组是降序的,此时current2都走到末尾了,在右区间已经是最小的了,还是比nums[current1]大,并且current1右边也是降序排列的
说明current1及其右边的区间都不满足要求,此时无需继续遍历,直接跳出循环就好
再来个升序版本
class Solution {int[] tmp;public int reversePairs(int[] record) {int length = record.length;tmp = new int[length];return reversePairsPlus(record, 0, length - 1);}private int reversePairsPlus(int[] nums, int left, int right) {if (left >= right) {return 0;}int count = 0;int middle = left + (right - left) / 2;count += reversePairsPlus(nums, left, middle);count += reversePairsPlus(nums, middle + 1, right);// 计算重要逆序对(升序排列下)int current1 = left;for (int j = middle + 1; j <= right; j++) {// 使用 long 防止整数溢出while (current1 <= middle && (long)nums[current1] <= 2L * (long)nums[j]) {current1++;}if (current1 > middle) break;count += (middle - current1 + 1);}// 合并有序数组(升序排列)int pos = 0;current1 = left;int current2 = middle + 1;while (current1 <= middle && current2 <= right) {if (nums[current1] <= nums[current2]) {tmp[pos] = nums[current1];current1++;} else {tmp[pos] = nums[current2];current2++;}pos++;}while (current1 <= middle) {tmp[pos] = nums[current1];current1++;pos++;}while (current2 <= right) {tmp[pos] = nums[current2];current2++;pos++;}// 复制回原数组System.arraycopy(tmp, 0, nums, left, right - left + 1);return count;}
}
