第二章、PyTorch 入门笔记：从张量基本操作到线性回归实战

目录

一、PyTorch 框架概述

1. 框架定位与核心优势

2. 主流深度学习框架对比

3. 安装方法

二、核心数据结构：张量（Tensor）

1. 张量的创建

（1）基础创建方法

（2）线性与随机张量

（3）特殊值张量（全 0、全 1、指定值）

2. 张量的类型转换

3. 张量与其他数据结构的转换

（1）张量 ↔ NumPy 数组

（2）标量张量 ↔ 普通数字

三、张量的核心操作

1. 数值计算

（1）基础运算（加减乘除）

（2）点乘与矩阵乘法

2. 常用运算函数

3. 索引操作

（1）简单行列索引

（2）列表索引

（3）范围索引

（4）布尔索引

（5）多维索引

4. 形状操作

（1）reshape ()：灵活调整形状

（2）squeeze () & unsqueeze ()：增减维度

（4）view () & contiguous ()：内存连续的形状调整

5. 拼接操作

四、自动微分：深度学习的核心引擎（重点！！！）

1. 核心原理

2. 实战示例

（1）标量张量的梯度计算

（2）矩阵张量的梯度计算

五、实战：用 PyTorch 实现线性回归

1. 流程概览

2. 完整代码实现

3. 关键说明

六、总结

---

PyTorch 入门笔记，知识点超密集，建议慢慢阅读！！

一、PyTorch 框架概述

1. 框架定位与核心优势

PyTorch 是一个基于 Python 的开源深度学习框架，由 Facebook（现 Meta）开发维护，核心是通过张量（Tensor） 封装数据并进行高效计算。与其他框架相比，其核心优势体现在：

• 易用性强：API 设计简洁直观，贴近 Python 原生语法，降低入门门槛。
• 动态计算图：支持运行时动态构建计算图，便于调试和灵活调整模型结构。
• 多场景支持：兼容计算机视觉（CV）、自然语言处理（NLP）、推荐系统等多领域任务，提供丰富的预训练模型和工具套件（如 TorchVision、TorchText）。
• 高效计算能力：支持多 GPU 并行计算、分布式训练，结合 CUDA 实现硬件加速。
• 生态成熟：拥有庞大的社区支持，大量开源项目、教程和第三方工具（如 TensorBoard）可直接复用。

2. 主流深度学习框架对比

框架	核心特点	适用场景	缺点
PyTorch	动态计算图、API 简洁、调试友好	科研实验、快速原型开发、中小型项目	早期在工业界部署支持较弱（现已通过 TorchScript 改善）
TensorFlow	静态计算图、部署生态完善	大规模工业级应用、移动端 / 嵌入式部署	API 较复杂，入门难度高
Caffe	层结构清晰、适合固定网络架构	传统计算机视觉任务（如图像分类）	灵活性差，难以适配复杂模型
飞桨（PaddlePaddle）	中文文档丰富、本土化支持好	国内企业级应用、教育场景	国际社区影响力较弱

3. 安装方法

推荐使用 pip 结合国内镜像源安装（以 PyTorch 1.10.0 为例，适配 Python 3.6+）：

pip install torch===1.10.0 -i https://pypi.tuna.tsinghua.edu.cn/simple

安装完成后，可通过以下代码验证：

import torch
print(torch.__version__)  # 输出torch版本号，如1.10.0
print(torch.cuda.is_available())  # 若支持GPU，输出True

二、核心数据结构：张量（Tensor）

张量是 PyTorch 中最基础的数据结构，可理解为 “多维数组”，支持标量（0 维）、向量（1 维）、矩阵（2 维）及更高维度的数值存储。所有深度学习计算均围绕张量展开。

1. 张量的创建

PyTorch 提供多种创建张量的方法，适用于不同场景：

（1）基础创建方法

1. torch.tensor根据指定数据（列表、numpy 数组等）创建张量
2. torch.Tensor 根据形状创建张量, 其也可用来创建指定数据的张量
3. torch.IntTensor、torch.FloatTensor、torch.DoubleTensor 创建指定类型的张量

代码示例：

"""
torch.tensor根据指定数据（列表、numpy 数组等）创建张量
"""
import torch #需要安装torch库
import numpy as np# 1.创建张量标量
data = torch.tensor(10)
print(data)
print("----------")
# 2.numpy数组创建张量
data = np.random.randn(2, 3)
data = torch.tensor(data)
print(data)
print("----------")
# 3.列表创建张量
data = [[10,20,30], [40,50,60]]
data = torch.tensor(data)
print(data)
print("----------")"""
打印结果：
tensor(10)
----------
tensor([[ 0.6643, -0.6231,  0.6080],[-0.5676, -0.6049,  0.1074]], dtype=torch.float64)
----------
tensor([[10, 20, 30],[40, 50, 60]])
----------"""

"""
torch.Tensor 根据形状创建张量, 其也可用来创建指定数据的张量
"""
import torch #需要安装torch库
import numpy as np#创建2行3列的张量、默认dtype为float32
data = torch.Tensor(2, 3)
print(data)
print("------------")
#如果传递列表作为参数，则会将列表中的元素作为张量的元素创建
data = torch.Tensor([10])
print(data)
print("------------")
data = torch.Tensor([10, 20])
print(data)"""
打印结果：
tensor([[0., 0., 0.],[0., 0., 0.]])
------------
tensor([10.])
------------
tensor([10., 20.])
"""

"""
torch.IntTensor、torch.FloatTensor、torch.DoubleTensor 创建指定类型的张量
"""
import torch #需要安装torch库
import numpy as np#创建2行3列的张量，数据类型为int32
data = torch.IntTensor(2, 3)
print(data)
print("-------------")#如果传递的元素类型不正确的话，则会进行类型转换
data = torch.IntTensor([2.5,3.3])
print(data)
print("-------------")#其它类型的张量
data = torch.ShortTensor()  # int16
print(data)
print("-------------")
data = torch.LongTensor()   # int64
print(data)
print("-------------")
data = torch.FloatTensor()  # float32
print(data)
print("-------------")
data = torch.DoubleTensor() # float64
print(data)
print("-------------")
"""
打印结果：
tensor([[0, 0, 0],[0, 0, 0]], dtype=torch.int32)
-------------
tensor([2, 3], dtype=torch.int32)
-------------
tensor([], dtype=torch.int16)
-------------
tensor([], dtype=torch.int64)
-------------
tensor([])
-------------
tensor([], dtype=torch.float64)
-------------"""

（2）线性与随机张量

• 线性张量：生成有序数值序列

"""
torch.arange()、torch.linspace() 创建线性张量"""
import torch #需要安装torch库
import numpy as np#  在指定区间按照步长生成元素 [start, end, step)
# 在 0 到 10 之间，按照步长 2 生成一系列数值。
# 生成的数值包括 0，但不包括 10
data = torch.arange(0, 10, 2)
print(data)
print("-------------")
# 2. 在指定区间按照元素个数生成 [start, end, steps]
#在 0 到 9 这个区间内生成 11 个等间隔的数值。
# 生成的数值会包括起始点 0 和结束点 9。
data = torch.linspace(0, 9, 11)
print(data)
print("-------------")
"""
打印结果：
tensor([0, 2, 4, 6, 8])
-------------
tensor([0.0000, 0.9000, 1.8000, 2.7000, 3.6000, 4.5000, 5.4000, 6.3000, 7.2000,8.1000, 9.0000])
-------------
"""

• 随机张量：生成符合特定分布的随机值，需注意随机种子确保可复现

"""
torch.random.manual_seed() 随机数种子设置，torch.randn() 创建随机张量"""
import torch #需要安装torch库
import numpy as np# 1. 创建随机张量
# torch.randn(2, 3) 函数用于生成一个 2 行 3 列的张量，
# 其中的元素是从标准正态分布（均值为 0，标准差为 1 的正态分布）中随机抽取的。
data = torch.randn(2, 3)
# torch.rand(2, 3) 函数用于生成一个 2 行 3 列的张量，
# 其中的元素是从均匀分布（范围在 [0, 1) 之间的均匀分布）中随机抽取的。
# data = torch.rand(2, 3)
print(data)
# 查看随机数种子
print('随机数种子:', torch.random.initial_seed())# 2. 随机数种子设置
torch.random.manual_seed(100)
data = torch.randn(2, 3)
print(data)
print('随机数种子:', torch.random.initial_seed())"""
随机种子不同，生成的随机数也不同。
最后打印结果：
tensor([[-2.1100,  1.9628,  1.0324],[ 0.3729, -0.4494,  0.2837]])
随机数种子: 70608466369400
tensor([[ 0.3607, -0.2859, -0.3938],[ 0.2429, -1.3833, -2.3134]])
随机数种子: 100"""

（3）特殊值张量（全 0、全 1、指定值）

# 1. 全0张量
torch.zeros(2, 3)  # 输出：tensor([[0., 0., 0.],[0., 0., 0.]])
torch.zeros_like(torch.tensor([[1,2],[3,4]]))  # 根据已有张量形状创建全0张量# 2. 全1张量
torch.ones(2, 3)  # 输出：tensor([[1., 1., 1.],[1., 1., 1.]])
torch.ones_like(torch.tensor([[1,2],[3,4]]))  # 根据已有张量形状创建全1张量# 3. 全为指定值的张量
torch.full([2, 3], 10)  # 输出：tensor([[10, 10, 10],[10, 10, 10]])
torch.full_like(torch.tensor([[1,2],[3,4]]), 20)  # 输出：tensor([[20,20],[20,20]])

2. 张量的类型转换

PyTorch 支持多种数据类型（如 int32、float32、float64 等），可通过以下方法转换：

# 方法1：使用.type()函数
data = torch.full([2,3], 10)  # 默认int64
print(data.dtype)  # 输出：torch.int64
data = data.type(torch.DoubleTensor)  # 转换为float64
print(data.dtype)  # 输出：torch.float64# 方法2：使用快捷方法（如double()、int()等）
data = torch.full([2,3], 10)
data = data.double()  # 等价于type(torch.DoubleTensor)
print(data.dtype)  # 输出：torch.float64

3. 张量与其他数据结构的转换

（1）张量 ↔ NumPy 数组

• 张量转 NumPy：使用numpy()方法，默认共享内存（修改一方会影响另一方），可通过copy()避免

  data_tensor = torch.tensor([2,3,4])
  data_numpy = data_tensor.numpy()  # 共享内存
  data_numpy[0] = 100
  print(data_tensor)  # 输出：tensor([100, 3, 4])# 避免共享内存
  data_numpy = data_tensor.numpy().copy()
  data_numpy[0] = 200
  print(data_tensor)  # 输出：tensor([100, 3, 4])（不受影响）
  

• NumPy 转张量：两种方式，区别在于是否共享内存

• 方法1：torch.from_numpy()，共享内存

• 方法2：torch.tensor()，不共享内存

  data_numpy = np.array([2,3,4])# 方法1：torch.from_numpy()，共享内存
  data_tensor1 = torch.from_numpy(data_numpy)
  data_tensor1[0] = 100
  print(data_numpy)  # 输出：[100  3  4]# 方法2：torch.tensor()，不共享内存
  data_tensor2 = torch.tensor(data_numpy)
  data_tensor2[0] = 200
  print(data_numpy)  # 输出：[100  3  4]（不受影响）
  

（2）标量张量 ↔ 普通数字

对于仅含一个元素的张量，使用item()方法提取为 Python 原生数字：

data = torch.tensor(30)  # 标量张量
print(data.item())  # 输出：30（int类型）data = torch.tensor([50.])  # 单元素向量张量
print(data.item())  # 输出：50.0（float类型）

三、张量的核心操作

1. 数值计算

（1）基础运算（加减乘除）

PyTorch 支持两种风格的运算：函数式（如add()）和运算符重载（如+），且带下划线的函数（如add_()）会直接修改原张量（in-place 操作）。

加减乘除取负号：

add、sub、mul、div、neg

add_、sub_、mul_、div_、neg_（其中带下划线的版本会修改原数据）

data = torch.randint(0, 10, [2, 3])  # 生成2x3的随机整数张量
print(data)  # 输出：tensor([[3,7,4],[0,0,6]])# 1. 不修改原张量
new_data = data.add(10)  # 等价于 data + 10
print(new_data)  # 输出：tensor([[13,17,14],[10,10,16]])# 2. 修改原张量（in-place）
data.add_(10)  # 等价于 data += 10
print(data)  # 输出：tensor([[13,17,14],[10,10,16]])# 其他基础运算
print(data.sub(5))  # 减法：data - 5
print(data.mul(2))  # 乘法：data * 2
print(data.div(3))  # 除法：data / 3
print(data.neg())   # 取负：-data

（2）点乘与矩阵乘法

• 点乘（Hadamard 积）：对应元素相乘，要求两个张量形状完全一致，使用mul()或*实现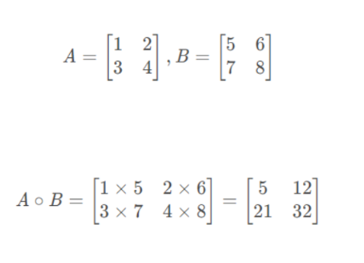

  

  
  data1 = torch.tensor([[1,2],[3,4]])
  data2 = torch.tensor([[5,6],[7,8]])
  print(torch.mul(data1, data2))  # 输出：tensor([[5,12],[21,32]])
  print(data1 * data2)  # 等价于mul()，输出相同

• 矩阵乘法：遵循线性代数中的矩阵乘法规则（前一个矩阵列数 = 后一个矩阵行数），使用matmul()或   @ 实现

  # data1: 3x2（3行2列），data2: 2x2（2行2列），结果：3x2
  data1 = torch.tensor([[1,2],[3,4],[5,6]])
  data2 = torch.tensor([[5,6],[7,8]])print(data1 @ data2)  # 输出：tensor([[19,22],[43,50],[67,78]])
  print(torch.matmul(data1, data2))  # 等价于@，输出相同
  

2. 常用运算函数

PyTorch 为张量封装了丰富的统计与数学运算函数，以下为高频使用场景：

import torch
data = torch.randint(0, 10, [2, 3], dtype=torch.float64)  # 2x3的float64张量
print(data)  # 输出：tensor([[4.,0.,7.],[6.,3.,5.]], dtype=torch.float64)# 1. 统计类函数
print(data.mean())        # 全局均值：4.1667
print(data.mean(dim=0))   # 按列求均值：tensor([5.0,1.5,6.0])
print(data.sum(dim=1))    # 按行求和：tensor([11.,14.])# 2. 数学类函数
print(torch.pow(data, 2)) # 平方：tensor([[16.,0.,49.],[36.,9.,25.]])
print(data.sqrt())        # 平方根：tensor([[2.0,0.0,2.6458],[2.4495,1.7321,2.2361]])
print(data.exp())         # 指数（e^x）：tensor([[54.598,1.0,1096.633],[403.428,20.085,148.413]])
print(data.log())         # 自然对数：tensor([[1.3863, -inf, 1.9459],[1.7918,1.0986,1.6094]])

3. 索引操作

张量索引与 NumPy 数组类似，支持多种方式提取指定元素，核心场景包括：1.简单行列索引 2.列表索引 3.范围索引 4.布尔索引 5.多维索引

（1）简单行列索引

data = torch.randint(0, 10, [4, 5])  # 4x5的随机张量
print(data)  # 输出：tensor([[0,7,6,5,9],[6,8,3,1,0],[6,3,8,7,3],[4,9,5,3,1]])print(data[0])       # 第0行：tensor([0,7,6,5,9])
print(data[:, 0])    # 第0列：tensor([0,6,6,4])
print(data[1, 2])    # 第1行第2列：tensor(3)

（2）列表索引

通过列表指定行 / 列，提取非连续的元素：

# 提取(0,1)和(1,2)位置的元素
print(data[[0,1], [1,2]])  # 输出：tensor([7,3])# 提取0、1行的1、2列（形成2x2张量）
print(data[[[0],[1]], [1,2]])  # 输出：tensor([[7,6],[8,3]])

（3）范围索引

使用:指定连续范围，格式为start:end:step（默认 step=1，start 省略为 0，end 省略为末尾）：

print(data[:3, :2])   # 前3行，前2列：tensor([[0,7],[6,8],[6,3]])
print(data[2:, :2])   # 第2行及以后，前2列：tensor([[6,3],[4,9]])
print(data[:, 1:4:2]) # 所有行，第1-4列（步长2）：tensor([[7,5],[8,1],[3,7],[9,3]])

（4）布尔索引

通过布尔条件筛选元素，适用于按条件过滤数据：

# 筛选第三列（索引2）大于5的所有行
print(data[data[:, 2] > 5])  # 输出：tensor([[0,7,6,5,9],[6,3,8,7,3]])# 筛选第二行（索引1）大于5的所有列
print(data[:, data[1] > 5])  # 输出：tensor([[0,7],[6,8],[6,3],[4,9]])

（5）多维索引

对于 3 维及以上张量，按 “轴（dim）” 依次指定索引：

data = torch.randint(0, 10, [3, 4, 5])  # 3x4x5的3维张量print(data[0, :, :])  # 第0个“块”的所有行和列（4x5）
print(data[:, 0, :])  # 所有“块”的第0行（3x5）
print(data[:, :, 0])  # 所有“块”的第0列（3x4）

4. 形状操作

张量形状调整是数据预处理和模型输入适配的核心步骤，常用函数包括：reshape()、squeze()、unsqueeze()、transpose()、permute()、view()、contiguous()等函数

（1）reshape ()：灵活调整形状

函数可以在保证张量数据不变的前提下改变数据的维度，将其转换成指定的形状。

data = torch.tensor([[10,20,30],[40,50,60]])  # 2x3张量
print(data.reshape(1, 6))  # 转为1x6：tensor([[10,20,30,40,50,60]])
print(data.reshape(3, 2))  # 转为3x2：tensor([[10,20],[30,40],[50,60]])
print(data.reshape(-1, 2)) # -1表示自动计算维度（此处为3）：# tensor([[10,20],[30,40],[50,60]])

（2）squeeze () & unsqueeze ()：增减维度

• squeeze(dim)：删除形状为 1 的维度（若不指定 dim，删除所有 1 维）
• unsqueeze(dim)：在指定轴添加形状为 1 的维度

import torch data = torch.tensor([1,2,3,4,5])  # 1维张量（shape: [5]）
print("data:",data)
print("------------")
# 增加维度
data1 = data.unsqueeze(dim=0)  # shape: [1,5]（在第0轴添加维度）
print("data1:",data1)
print("-----------")
data2 = data.unsqueeze(dim=1)  # shape: [5,1]（在第1轴添加维度）
print("data2:",data2)
print("------------")
# 删除维度
data3 = data1.squeeze()        # shape: [5]（删除data1中所有1维）
print("data3:",data3)
print("------------")
data4 = data2.squeeze(dim=1)   # shape: [5]（仅删除data2中第1轴的1维）
print("data4:",data4)
print("------------")
"""
打印结果：
data: tensor([1, 2, 3, 4, 5])
------------
data1: tensor([[1, 2, 3, 4, 5]])
-----------
data2: tensor([[1],[2],[3],[4],[5]])
------------
data3: tensor([1, 2, 3, 4, 5])
------------
data4: tensor([1, 2, 3, 4, 5])
------------
"""

（3）transpose () & permute ()：transpose 函数可以实现交换张量形状的指定维度, 例如: 一个张量的形状为 (2, 3, 4) 可以通过 transpose 函数把 3 和 4 进行交换, 将张量的形状变为 (2, 4, 3) 。 permute 函数可以一次交换更多的维度。

• transpose(dim1, dim2)：交换两个指定轴的维度
• permute(dims)：一次性交换多个轴（需指定所有轴的新顺序）

import torchdata = torch.randint(0, 10, [2,3,4])  # 生成2x3x4的3维张量
print("data:",data)
print(data.shape)
print("--------")
# 交换第1和第2轴（shape变为2x4x3）
data1 = torch.transpose(data, 1, 2)
print("data1:",data1)
print(data1.shape)
print("--------")
# 一次性调整为3x4x2的顺序（指定所有轴的新顺序：[1,2,0]）
data2 = data.permute([1,2,0])
print("data2:",data2)
print(data2.shape)
print("--------")"""
打印结果：
data: tensor([[[3, 7, 3, 0],[7, 3, 4, 8],[9, 6, 0, 0]],[[0, 1, 3, 2],[2, 1, 3, 0],[4, 4, 3, 8]]])
torch.Size([2, 3, 4])
--------
data1: tensor([[[3, 7, 9],[7, 3, 6],[3, 4, 0],[0, 8, 0]],[[0, 2, 4],[1, 1, 4],[3, 3, 3],[2, 0, 8]]])
torch.Size([2, 4, 3])
--------
data2: tensor([[[3, 0],[7, 1],[3, 3],[0, 2]],[[7, 2],[3, 1],[4, 3],[8, 0]],[[9, 4],[6, 4],[0, 3],[0, 8]]])
torch.Size([3, 4, 2])
--------
"""

（4）view () & contiguous ()：内存连续的形状调整

        view 函数也可以用于修改张量的形状，只能用于存储在整块内存中的张量。

        在 PyTorch 中，有些张量是由不同的数据块组成的，它们并没有存储在整块的内存中，view 函数无法对这样的张量进行变形处理，

        例如: 若张量经过transpose()、permute()等操作后内存不连续，就无法使用 view 函数进行形状操作，需先通过contiguous()转为连续内存：

data = torch.tensor([[10,20,30],[40,50,60]])  # 内存连续
print(data.is_contiguous())  # 输出：True# 1. 直接使用view()
data1 = data.view(3,2)  # 输出：tensor([[10,20],[30,40],[50,60]])# 2. 经transpose()后内存不连续，需先contiguous()
data2 = torch.transpose(data, 0, 1)  # 交换轴后内存不连续
print(data2.is_contiguous())  # 输出：False
data3 = data2.contiguous().view(2,3)  # 转为连续内存后再调整形状

5. 拼接操作

使用torch.cat([tensor1, tensor2, ...], dim)按指定轴拼接多个张量，要求除拼接轴外，其他轴形状完全一致：

import torch#设置随机数种子
torch.manual_seed(1)data1 = torch.randint(0,10, [1,2,3])  # shape: [1,2,3]
print("data1:", data1)
print("--------")
data2 = torch.randint(0,10, [1,2,3])  # shape: [1,2,3]
print("data2:", data2)
print("--------")
# 按第0轴拼接（shape变为[2,2,3]）
cat0 = torch.cat([data1, data2], dim=0)
print("cat0:", cat0)
print("--------")
# 按第1轴拼接（shape变为[1,4,3]）
cat1 = torch.cat([data1, data2], dim=1)
print("cat1:", cat1)
print("--------")
# 按第2轴拼接（shape变为[1,2,6]）
cat2 = torch.cat([data1, data2], dim=2)
print("cat2:", cat2)
print("--------")"""
打印结果：
data1: tensor([[[5, 9, 4],[8, 3, 3]]])
--------
data2: tensor([[[1, 1, 9],[2, 8, 9]]])
--------
cat0: tensor([[[5, 9, 4],[8, 3, 3]],[[1, 1, 9],[2, 8, 9]]])
--------
cat1: tensor([[[5, 9, 4],[8, 3, 3],[1, 1, 9],[2, 8, 9]]])
--------
cat2: tensor([[[5, 9, 4, 1, 1, 9],[8, 3, 3, 2, 8, 9]]])
--------"""

四、自动微分：深度学习的核心引擎（重点！！！）

        PyTorch 的torch.autograd模块实现了自动微分功能，是反向传播算法的底层支撑，能够自动计算损失函数对模型参数的梯度，从而实现参数更新。

这里只记录了在PyTorch中的用法，后续会有详细记录原理。

1. 核心原理

• 计算图：将张量运算抽象为有向无环图（DAG），节点为张量，边为运算操作。

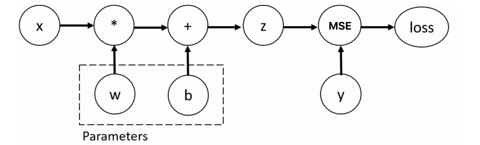
• requires_grad=True：为张量标记 “需要计算梯度”，后续所有依赖该张量的运算都会被记录到计算图中。
• backward()：从损失函数张量出发，沿计算图反向传播，自动计算所有requires_grad=True张量的梯度，并存储在tensor.grad属性中。

2. 实战示例

（1）标量张量的梯度计算

import torchdef scalar_grad():x = torch.tensor(5)  # 输入标量（无需计算梯度）y = torch.tensor(0., dtype=torch.float32)  # 目标值# 模型参数：w（权重）和b（偏置），需计算梯度w = torch.tensor(1., requires_grad=True, dtype=torch.float32)b = torch.tensor(3., requires_grad=True, dtype=torch.float32)# 前向传播：z = x*w + bz = x * w + b# 损失函数：MSE（均方误差）loss = torch.nn.MSELoss()(z, y)# 反向传播：自动计算梯度、也就是自动微分模块loss.backward()# 输出梯度（w.grad = 2*(z-y)*x = 2*(8-0)*5=80；b.grad=2*(z-y)=16）print("w的梯度:", w.grad)  # 输出：tensor(80.)print("b的梯度:", b.grad)  # 输出：tensor(16.)scalar_grad()

（2）矩阵张量的梯度计算

def matrix_grad():x = torch.ones(2, 5)  # 输入：2x5矩阵（无需计算梯度）y = torch.zeros(2, 3)  # 目标值：2x3矩阵# 模型参数：w（5x3）和b（3），需计算梯度w = torch.randn(5, 3, requires_grad=True)b = torch.randn(3, requires_grad=True)# 前向传播：z = x @ w + b（矩阵乘法+偏置）z = torch.matmul(x, w) + b# 损失函数：MSEloss = torch.nn.MSELoss()(z, y)# 反向传播loss.backward()# 输出梯度（w.grad形状与w一致，b.grad形状与b一致）print("w的梯度:\n", w.grad)print("b的梯度:", b.grad)matrix_grad()

五、实战：用 PyTorch 实现线性回归

        线性回归是最基础的机器学习模型，通过拟合线性关系y = wx + b预测连续值。以下基于 PyTorch 完成完整流程，涵盖数据准备、模型构建、训练与可视化。

1. 流程概览

PyTorch 模型开发遵循固定流程：

1. 准备数据集：生成或加载训练数据，封装为 PyTorch 可处理的格式。
2. 构建模型：定义线性回归模型结构。
3. 设置损失函数与优化器：选择 MSE 损失函数和 SGD 优化器。
4. 模型训练：迭代训练，通过反向传播更新参数。
5. 结果可视化：分析损失变化和拟合效果。

2. 完整代码实现

import torch
from torch.utils.data import TensorDataset, DataLoader
from torch import nn, optim
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt# 配置中文字体 - 确保图表能正确显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体作为中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题# 1. 准备数据集
def create_dataset():# 使用sklearn生成线性回归数据（1个特征，100个样本，带噪声）x, y, coef = make_regression(n_samples=100,  # 生成100个样本n_features=1,  # 每个样本只有1个特征noise=10,  # 添加高斯噪声，标准差为10coef=True,  # 返回真实系数bias=1.5,  # 设置偏置项(截距)为1.5random_state=0  # 随机种子，确保每次生成相同数据)# 转换为PyTorch张量x = torch.tensor(x, dtype=torch.float32)y = torch.tensor(y, dtype=torch.float32)return x, y, coef# 2. 构建数据加载器（支持批量训练和乱序）
x, y, coef = create_dataset()  # 获取数据
dataset = TensorDataset(x, y)  # 将特征和标签封装为数据集对象# 创建数据加载器，支持批量处理和乱序
dataloader = DataLoader(dataset=dataset,batch_size=16,  # 每批处理16个样本shuffle=True  # 训练前打乱数据顺序，防止模型学习到顺序信息
)# 3. 构建线性回归模型（输入1维，输出1维）
model = nn.Linear(in_features=1, out_features=1)  # 创建线性层 y = wx + b# 4. 设置损失函数和优化器
criterion = nn.MSELoss()  # 均方误差损失，用于回归问题
optimizer = optim.SGD(model.parameters(), lr=1e-2)  # 随机梯度下降优化器，学习率0.01# 5. 模型训练
epochs = 100  # 训练轮数
loss_history = []  # 记录每轮损失，用于后续可视化for epoch in range(epochs):total_loss = 0.0  # 累计损失total_samples = 0  # 累计样本数# 遍历数据加载器中的每个批次for train_x, train_y in dataloader:# 前向传播：使用模型预测输出y_pred = model(train_x)# 计算损失（需统一形状：train_y从1维转为2维，与y_pred形状匹配）loss = criterion(y_pred, train_y.reshape(-1, 1))# 反向传播与参数更新optimizer.zero_grad()  # 清空上一轮梯度，防止梯度累积loss.backward()  # 计算梯度，反向传播optimizer.step()  # 更新模型参数# 累计损失和样本数（用于计算平均损失）total_loss += loss.item() * train_x.size(0)  # loss.item()获取标量损失值total_samples += train_x.size(0)  # 当前批次的样本数# 计算每轮平均损失avg_loss = total_loss / total_samplesloss_history.append(avg_loss)  # 记录损失历史# 每10轮打印一次损失if (epoch + 1) % 10 == 0:print(f"Epoch [{epoch + 1}/{epochs}], Loss: {avg_loss:.4f}")# 6. 结果可视化
# 创建图表，设置大小
plt.figure(figsize=(12, 4))# （1）损失变化曲线
plt.subplot(1, 2, 1)  # 1行2列的第1个子图
plt.plot(range(epochs), loss_history)
plt.title('损失变化曲线')
plt.xlabel('训练轮数')
plt.ylabel('MSE损失')
plt.grid()  # 添加网格线# （2）拟合效果对比
plt.subplot(1, 2, 2)  # 1行2列的第2个子图
# 绘制原始数据散点图
plt.scatter(x.numpy(), y.numpy(), label='真实数据', alpha=0.6)# 生成预测用的x值（覆盖数据范围）
# linspace(start, stop, num)：生成等差数列
x_pred = torch.linspace(x.min(), x.max(), 1000).reshape(-1, 1)
# 使用训练好的模型进行预测，并转换为numpy数组
y_pred = model(x_pred).detach().numpy()  # detach()将张量从计算图中分离# 真实线性关系（y = coef*x + 1.5）
y_true = x_pred.numpy() * coef + 1.5# 绘制模型拟合的直线
plt.plot(x_pred.numpy(), y_pred, label='模型拟合', color='orange', linewidth=2)
# 绘制真实关系的直线（红色虚线）
plt.plot(x_pred.numpy(), y_true, label='真实关系', color='red', linestyle='--')
plt.title('线性回归拟合效果')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()  # 显示图例
plt.grid()  # 添加网格线# 调整子图间距，避免重叠
plt.tight_layout()
# 显示图表
plt.show()# 输出训练得到的参数（接近真实值coef和1.5）
print(f"真实权重: {coef:.4f}, 训练权重: {model.weight.item():.4f}")
print(f"真实偏置: 1.5, 训练偏置: {model.bias.item():.4f}")

"""
运行结果：
Epoch [10/100], Loss: 243.9083
Epoch [20/100], Loss: 121.8699
Epoch [30/100], Loss: 114.6820
Epoch [40/100], Loss: 114.5848
Epoch [50/100], Loss: 114.3511
Epoch [60/100], Loss: 114.3338
Epoch [70/100], Loss: 114.3942
Epoch [80/100], Loss: 114.3212
Epoch [90/100], Loss: 114.3931
Epoch [100/100], Loss: 114.3406"""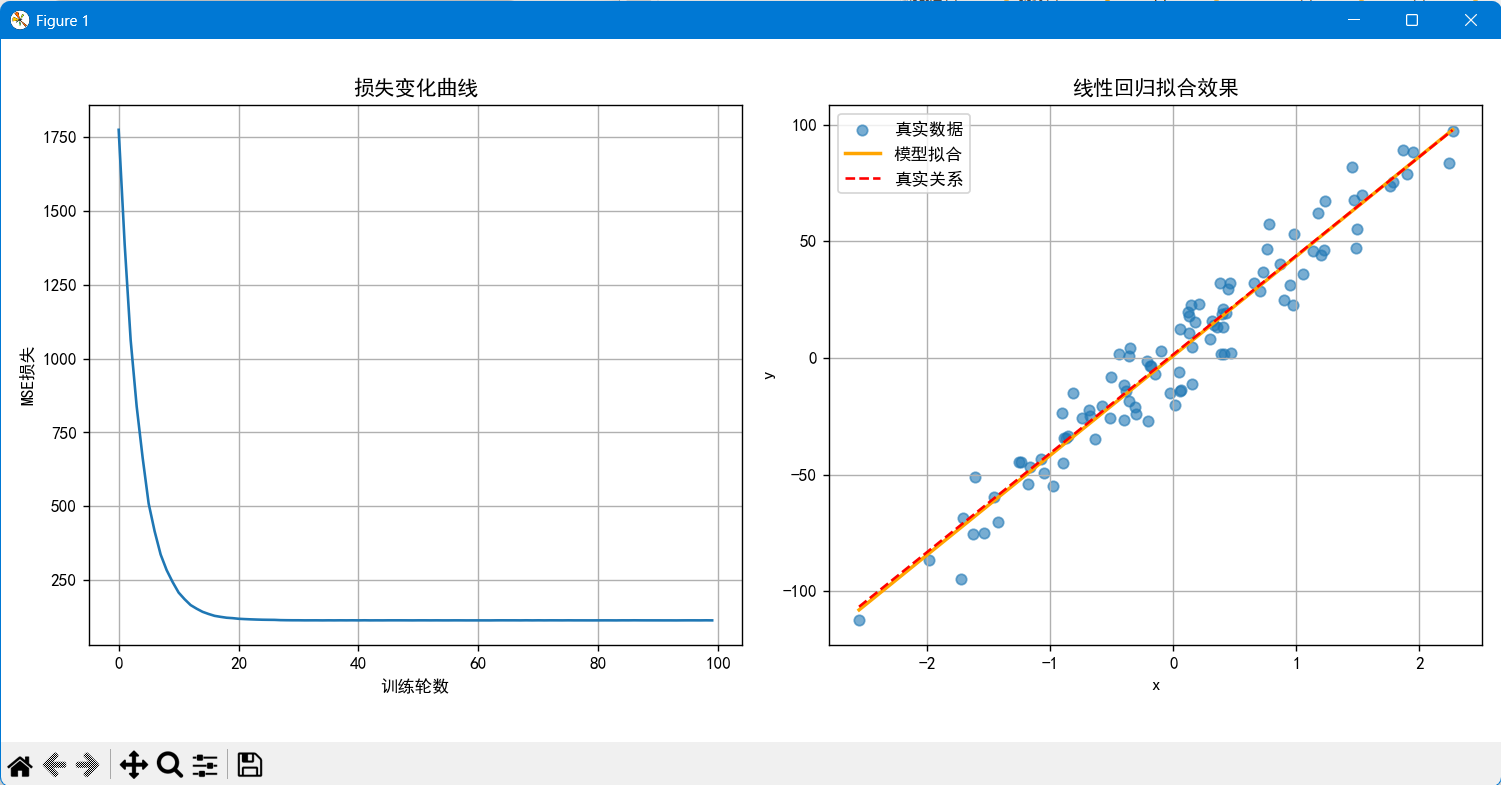

3. 关键说明

• 数据加载器（DataLoader）：自动实现批量加载和数据乱序，提升训练效率和泛化能力。
• 模型定义：nn.Linear是 PyTorch 内置的线性层，自动封装y = wx + b的计算逻辑。
• 梯度清零（optimizer.zero_grad ()）：PyTorch 默认累积梯度，每轮训练前需手动清空，避免影响当前轮次计算。
• detach()：预测时使用detach()脱离计算图，避免不必要的梯度计算，提升效率。

六、总结

1. 张量是基础：所有操作围绕张量展开，需熟练掌握创建、转换、索引、形状调整等基础技能。
2. 自动微分是核心：通过requires_grad和backward()实现梯度自动计算，无需手动推导公式。
3. 模型开发流程固定：数据准备→模型构建→损失与优化器→训练迭代，该流程可迁移至复杂模型。