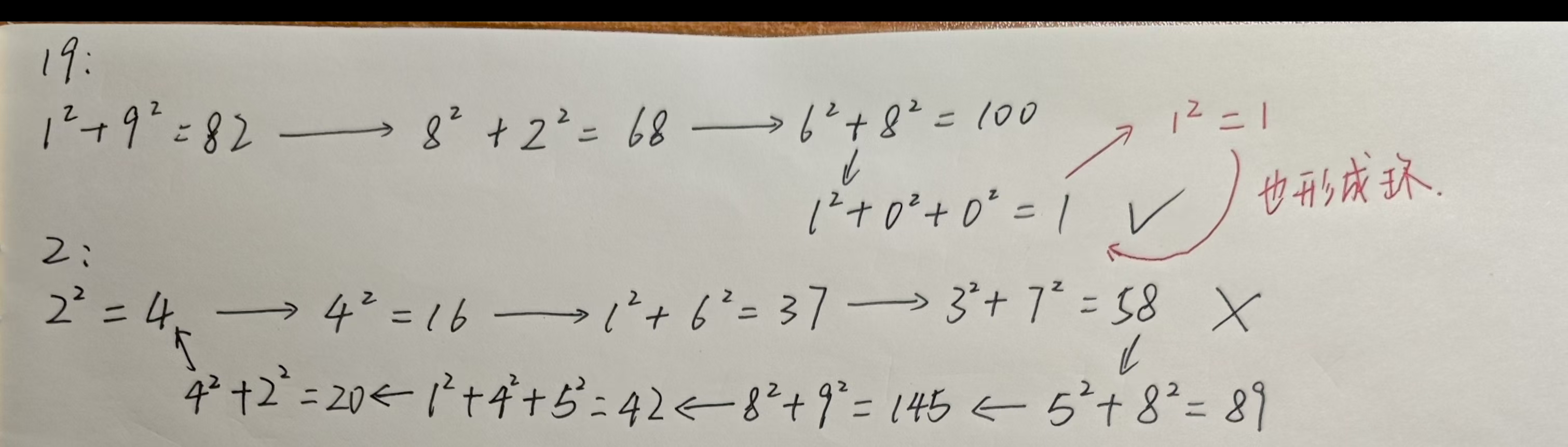当前位置：首页 > news >正文

算法之双指针

news 2025/9/9 15:37:38

在算法设计中，双指针是一种高效优化工具，主要用于线性数据结构（如数组（数组划分和数组分块常用）、链表、字符串），通过控制两个指针的移动轨迹，将原本需要 O (n²) 时间复杂度的问题优化为 O (n)，核心优势是无需额外空间（通常为 O (1) 空间复杂度）且逻辑直观。其常见形式分为同向指针，对撞指针和快慢指针，具体解析如下：

(一) 同向指针

1. 定义与核心场景
同向指针是双指针的另一种核心形式，指两个指针沿同一方向移动（如均从左到右），初始位置通常有先后关系（或起始于同一位置）

核心用途是在线性结构（如数组、链表）中进行原地元素筛选、位置调整或边界划分，无需依赖数据的有序性，更侧重通过指针分工实现元素的 “有效区域” 与 “待处理区域” 分离

2. 移动逻辑
同向指针的核心是 “分工协作”：一个指针（通常称为 “慢指针”）标记 “有效元素区域” 的边界，另一个指针（通常称为 “快指针”）负责遍历所有元素并筛选目标元素，两者同方向移动但节奏不同：

慢指针（slow）：初始位置通常为序列起点（如索引 0）或特殊标记（如 - 1），仅当快指针找到 “有效元素” 时才移动，用于记录 “已处理的有效元素” 的末尾位置；
快指针（fast）：从序列起点开始，始终向前移动（如每次 + 1），负责遍历所有元素，判断当前元素是否符合 “有效” 条件（如非零、非目标值等）。

简单说：快指针 “探路”，慢指针 “驻守有效区域”；快指针遇到有效元素时，慢指针 “接纳” 并前移，遇到无效元素时，快指针独自前行，慢指针保持不动。

3. 终止条件
循环终止于快指针遍历完整个序列（如快指针到达数组末尾，即 fast == 序列长度）。此时慢指针的位置通常标记了 “有效元素区域” 的结束边界（如慢指针索引 + 1 为有效元素的数量）。

4. 适用场景
同向指针的核心优势是原地处理元素重排，且能保持有效元素的相对顺序，适用于以下场景：

移动特定元素：如 “移动零”（将所有 0 移到末尾，非零元素保持顺序）；
移除元素：如 “移除数组中等于 val 的元素”（剩余元素保持相对顺序）；
压缩序列：如 “删除字符串中的所有相邻重复项”“合并两个有序数组（原地）” 等。

(二) 对撞指针（左右指针）

1. 定义与核心场景
对撞指针又称 “左右指针”，其应用依赖于数据结构的有序性（如排序数组、对称字符串），核心用途是高效查找满足特定条件的元素或元素对，例如 “有序数组两数之和”“验证回文串”“反转字符串”“删除有序数组中的重复项（首尾验证版）” 等问题。
2. 移动逻辑
指针初始位置分别位于线性结构的两端，之后按照问题规则向中间同步逼近：

左指针（left）：从序列最左端（索引 0 或起始位置）开始，每次向右侧移动，一般为++left。
右指针（right）：从序列最右端（索引 n-1 或末尾位置）开始，每次向左侧移动，一般为--right。

3. 终止条件
终止时机需结合问题目标，核心分为两类：

指针相遇或错开：当无需提前匹配结果时，循环终止于left == right（两指针指向同一位置，覆盖所有元素）或left > right（两指针交叉，遍历完所有可能组合）；
提前匹配终止：若在移动过程中找到满足条件的结果（如nums[left] + nums[right] == target），可直接跳出循环，无需继续逼近。

(三) 快慢指针（龟兔赛跑算法）

1. 定义与核心思想
快慢指针又称 “龟兔赛跑算法”，其核心是让两个指针在同向移动的基础上，保持不同的移动速度（如 “慢指针 1 步 / 次，快指针 2 步 / 次”）。通过速度差，可在无需额外空间的前提下，检测序列的循环特性或定位特定位置。
2. 适用场景
快慢指针的核心优势是处理 “循环相关” 或 “特定位置定位” 问题，常见场景包括：

环形结构检测：如判断链表是否有环、找到环形链表的入口；
特定位置定位：如查找链表的中间节点（用于归并排序）、删除链表的倒数第 k 个节点；
重复元素查找：如在无额外空间的要求下，找到数组中的重复元素（如 LeetCode 287. 寻找重复数）。

3. 常见实现方式

快慢指针的速度差可根据问题灵活调整，最经典的实现是 “1:2 速度比”：

慢指针（slow）：每次移动 1 步（如slow = slow.next或slow += 1）；
快指针（fast）：每次移动 2 步（如fast = fast.next.next或fast += 2）。

原理类比：若序列存在环（如环形链表），快指针会像 “兔子” 一样在环内循环，最终追上慢指针（“乌龟”）；若序列无环（如普通链表），快指针会率先到达序列末尾（如链表的null节点），循环自然终止。
4. 其他变种实现
除了 “1:2 速度比”，快慢指针的速度差可根据目标调整：

定位链表倒数第 k 个节点：先让快指针超前慢指针 k 步，再让两者同步移动（均 1 步 / 次）；当快指针到达末尾时，慢指针恰好指向倒数第 k 个节点；
寻找数组中重复元素：让慢指针按 “1 步 / 次” 移动，快指针按 “nums [fast] 步 / 次” 移动（模拟循环），最终两指针会在重复元素位置相遇。

综上，双指针的选择需结合问题的数据结构特性（有序 / 无序、线性 / 环形）和目标需求（查找 / 检测 / 定位）：若处理有序结构的元素查找，优先考虑对撞指针；若处理循环或特定位置问题，优先考虑快慢指针。

(三) 题目

题目1：移动零

链接：283. 移动零 - 力扣（LeetCode）

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

核心思路：

该解法采用双指针（同向指针）策略，通过两个指针（dest和cur）划分数组区间，实现零元素的移动：

1.先定义两个指针——cur和dest

cur：从左往右扫描数组，遍历数组
dest：已处理的区间内，非零元素的最后一个元素

此时三个区间：

[0,dest] 非0区间
[dest+1,cur-1] 0区间
[cur,n-1] 待处理区间

cur遍历时：

遇到0元素：cur++
遇到非0元素：交换dest+1和cur元素，再dest++，cur++

小思考：

为何是交换，不是直接覆盖？

若直接覆盖，在后面还得直接加0才可以，但是你怎么知道它要加多少个0会超级麻烦，而交换就让非0元素全在左边。0元素全在右边，超级符合题目要求！

代码：

class Solution {
public:void moveZeroes(vector<int>& nums) {for(int dest = -1, cur = 0; cur < nums.size(); cur++){if(nums[cur]){swap(nums[++dest],nums[cur]);}}}
};

题目2：复写0

链接：1089. 复写零 - 力扣（LeetCode）

给你一个长度固定的整数数组 arr ，请你将该数组中出现的每个零都复写一遍，并将其余的元素向右平移。

注意：请不要在超过该数组长度的位置写入元素。请对输入的数组就地进行上述修改，不要从函数返回任何东西。

核心思路：

该解法采用双指针（同向指针）策略

1. 指针初始化——定义两个指针 cur 和 dest

2. 定位最后一个复写元素

结束条件：遍历数组直至 cur 或 dest 超出有效范围
遍历规则：

arr[cur]为0时dest走两步
arr[cur]部位0时dest走一步

3. 从后向前完成复写操作

arr[cur]为0时dest走两步并且赋值成0
arr[cur]部位0时dest走一步并拷贝cur的值

注意：边界处理

针对如[1, 5, 0, 0, 6, 0, 8, 9]这类可能导致 dest 越界的情况：

核心——预先处理最后一次复写

将 n-1 位置设为0
执行 cur-- 和 dest-=2 操作

代码：

class Solution {
public:void duplicateZeros(vector<int>& arr) {int cur = 0, dest = -1, n = arr.size();while (cur < n){if (arr[cur])dest++;elsedest += 2;if (dest >= n - 1)break;cur++;}if (dest == n){arr[n - 1] = 0;cur--;dest -= 2;}while (cur >= 0){if (arr[cur])arr[dest--] = arr[cur--];else{arr[dest--] = 0;arr[dest--] = 0;cur--;}}
}
};

题目3：快乐数

链接：202. 快乐数 - 力扣（LeetCode）

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

核心思路：

我们先来理解一下这个题目：

思路：

通过观察图片可以发现，这个问题可以类比链表的环检测，因此采用双指针（快慢指针）策略。

具体分析：

题目核心是判断数组是否存在环，且环内元素为1（即环的起始元素为1）
实际上，所有数据都会形成环。根据鸽巢原理（n个鸟巢，n+1个鸽子，至少又一个鸟巢里面的鸽子数大于1）：

最大数为2^31 - 1 ≈ 2.1×10^9
经过平方和运算后，结果范围在[1,810]之间（9^2×10=810）
当任意数x运算超过811次时，必然出现重复值形成环

实现步骤：

定义快慢指针
快指针每次前进两步，慢指针每次前进一步
判断相遇时是否为1

注意事项：虽然数字不是传统意义上的指针，但在这个问题中可以将其视为指针来操作

代码：

class Solution {
public:int bitSum(int n){int sum = 0;while(n){int a = n%10;sum += a*a;n/=10;}return sum;}bool isHappy(int n) {int slow = n, fast = bitSum(n);while(fast != slow){fast = bitSum(bitSum(fast));slow = bitSum(slow);}if(slow == 1)return true;elsereturn false;}
};

题目4：盛最多水的容器

链接：11. 盛最多水的容器 - 力扣（LeetCode）

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

核心思路：

1. 暴力解法
设两指针i , j，分别指向⽔槽板的最左端以及最右端，此时容器的宽度为 j - i 。由于容器的⾼度由两板中的短板决定，因此可得容积公式：v = (j - i) * min( height[i], height[j] )
但暴力解法需遍历所有可能的(i, j)组合，时间复杂度为O(n²)，会超出题目时间要求，因此需要优化。
2. 优化方法：双指针（左右指针）策略（利用单调性）
采用左右指针初始分别指向数组两端（left = 0，right = n-1），通过移动指针逐步缩小范围，高效寻找最大容积。
步骤：

初始化左右指针left和right，计算当前容积并记录为初始最大值；
比较 height[left] 和 height[right] 的大小，移动高度较小的一侧指针（若相等，移动任意一侧均可）；
重新计算新指针位置的容积，更新最大值；
重复2和3，直到左右指针相遇，此时记录的最大值即为结果。

移动较矮指针的原因：
假设当前height[left] < height[right]（左边界为短板）：容器的宽度为 right - left

若移动右指针（较长的一侧）：新宽度必然减小（right-1 - left < right - left），且新的有效高度仍由左边界决定（不会超过height[left]），因此容积一定会变小；
若移动左指针（较短的一侧）：虽然宽度减小，但可能遇到更高的左边界，新的有效高度可能增大（最多等于右边界高度），因此容积有可能变大。

同理，若height[right] < height[left]，则应移动右指针。

这种策略通过放弃 “必然更小” 的可能，保留 “潜在更大” 的机会，将时间复杂度优化至O(n)。

代码：

1.暴力解法：

//盛最多水的容器暴力解法
class Solution {
public:int maxArea(vector<int>& height) {int n = height.size();int ret = 0;for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){ret = max(ret, min(height[i], height[j]) * (j - i));}}return ret;}
};

2. 优化方法：双指针策略（利用单调性）


//盛最多水的容器优化解法
class Solution {
public:int maxArea(vector<int>& height) {int left = 0, right = height.size() - 1, ret = 0;while (left < right){int v = min(height[left], height[right]) * (right - left);ret = max(ret, v);if (height[left] < height[right])++left;else--right;}return ret;}
};

题目5：有效三角形的个数

链接：611. 有效三角形的个数 - 力扣（LeetCode）

给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

核心思路：

先来想想怎么判断三个数是否构成三角形

核心条件是：任意两边之和大于第三边。由于三角形中最长边会限制另外两边的和（若最长边小于另外两边之和，则其余两边的和必然大于第三边），因此更高效的判断方式是：最小的两边之和大于最长边。

代码思路：

1. 暴力解法

先对数组排序（方便后续判断大小关系），然后枚举所有可能的三元组(i, j, k)（需满足i < j < k），通过上述条件判断是否能组成三角形。

但这种方法需遍历所有三元组，时间复杂度为O(n³)，效率较低。

2. 优化方法：双指针（左右指针）策略（利用单调性）

核心逻辑：通过排序简化大小判断，固定最长边后，用双指针快速寻找符合条件的另外两条边，将时间复杂度降至O(n²)。

步骤：
1. 对数组排序（升序），便于利用 “最小两边之和> 最长边” 的条件；
2. 固定最长边：遍历数组，设当前最长边为nums[i]（i从 2 开始，确保至少有两个更小的数）；
3. 初始化双指针：

左指针left = 0（指向当前范围内最小的数）
右指针right = i - 1（指向当前范围内次大的数，即小于nums[i]的最大数）

4. 判断与计数：

若nums[left] + nums[right] > nums[i]：由于数组递增，left到right之间的所有数（nums[left], nums[left+1], ..., nums[right-1]）都大于等于nums[left]，因此它们与nums[right]的和必然也大于nums[i]。即此时left到right之间的所有数与nums[right]、nums[i]均可组成三角形，共有right - left个有效三元组，计入结果后将right左移（缩小范围继续寻找）
若nums[left] + nums[right] ≤ nums[i]：说明当前left对应的边太小，需右移left（增大两边之和，尝试满足条件）

5. 重复步骤4，直到left >= right，再继续固定下一个最长边i。

代码：

1. 暴力解法

//有效三角形的个数暴力解法
class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(), nums.end());int n = nums.size();int ret = 0;for (int i = 0; i < n; i++){for (int j = i + 1; j < n; j++){for (int k = j + 1; k < n; k++){if (nums[i] + nums[j] > nums[k])ret++;}}}return ret;}
};

2. 优化方法：双指针（左右指针）策略（利用单调性）

//有效三角形的个数优化解法
class Solution {
public:int triangleNumber(vector<int>& nums) {int n = nums.size() - 1;sort(nums.begin(), nums.end());int ret = 0;for (int i = n; i > 0; i--){int left = 0, right = i - 1;while (left < right){if (nums[left] + nums[right] > nums[i]){ret += (right - left);right--;}else{left++;}}}return ret;}
};

题目6：查找总价格为目标值的两个商品（和为s的两个数字）

链接：LCR 179. 查找总价格为目标值的两个商品 - 力扣（LeetCode）

购物车内的商品价格按照升序记录于数组 price。请在购物车中找到两个商品的价格总和刚好是 target。若存在多种情况，返回任一结果即可。

核心思路：

1. 暴力解法

定义两个指针i和j（i < j），遍历数组中所有可能的元素对，判断price[i] + price[j]是否等于target。若找到符合条件的 pair，直接返回{price[i], price[j]}。
但此方法需枚举所有组合，时间复杂度为O(n²)，在数据量较大时效率较低。

2. 优化方法：双指针（左右指针）策略（利用单调性）

因数组是升序排列的，可通过双指针快速缩小查找范围，将时间复杂度降至O(n)。
步骤：
1. 初始化指针：左指针left指向数组起始位置（0），右指针right指向数组末尾（n-1）；
2. 循环条件：当left < right时，持续判断两指针指向元素的和；
3. 具体判断：

若price[left] + price[right] == target：找到目标组合，直接返回{price[left], price[right]}；
若price[left] + price[right] < target：由于数组升序，right已指向当前范围内最大的元素，此时和仍小于目标值，说明price[left]过小，需增大左侧值，故将left右移（left++）；
若price[left] + price[right] > target：同理，left已指向当前范围内最小的元素，此时和仍大于目标值，说明price[right]过大，需减小右侧值，故将right左移（right--）。

代码：

1. 暴力解法

//和为s的两个数字暴力解法
class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {int n = price.size();for (int i = 0; i < n; i++){for (int j = i + 1; j < n; j++){if (price[i] + price[j] == target){return{ price[i],price[j] };}}}}
};

2. 优化方法：双指针（左右指针）策略（利用单调性）

//和为s的两个数字优化解法
class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {int left = 0, right = price.size() - 1;while (left < right){int sum = price[left] + price[right];if (sum == target){return { price[left], price[right] };}else if (sum > target)right--;elseleft++;}return { -1, -1 };}
};

题目7：三数之和

链接：15. 三数之和 - 力扣（LeetCode）

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

核心思路：

1. 暴力解法

先对数组排序（为去重做准备），枚举所有可能的三元组(i, j, k)，要求i < j < k，判断nums[i] + nums[j] + nums[k] == 0，若符合条件，将三元组加入结果集，同时通过跳过重复元素（相同值的i、j、k）避免重复三元组。
但是三层循环的时间复杂度为O(n³)，在数组长度较大时效率极低，无法满足时间要求。

2. 优化方法：双指针（左右指针）策略（利用单调性）

利用排序后数组的单调性，将三层循环降为两层，时间复杂度优化至O(n²)，同时通过去重步骤确保结果不重复。

步骤：

1. 排序：对数组升序排序。排序的作用有二：一是使重复元素相邻，便于去重；二是为双指针移动提供单调性基础。
2. 固定第一个数：遍历数组，固定三元组的第一个数nums[i]（i从 0 开始）。

若nums[i] > 0，由于数组升序，后续数均大于等于nums[i]，三数之和必大于 0，可直接终止循环。

3. 双指针找剩余两数：在i右侧的子数组[i+1, n-1]中，用左指针left = i+1、右指针right = n-1寻找满足nums[left] + nums[right] = -nums[i]的组合：

若nums[left] + nums[right] < -nums[i]：需增大两数之和，将left右移（利用升序特性，右侧数更大）；
若nums[left] + nums[right] > -nums[i]：需减小两数之和，将right左移；
若相等：找到有效三元组，加入结果集。

4. 去重操作（关键）：

固定数去重：当i > 0且nums[i] == nums[i-1]时，跳过当前i（避免重复固定相同的数，导致相同三元组）；
双指针针去重：找到有效三元组后，需同时将left右移、right左移，并跳过所有与当前left、right相同的元素（避免同一i下出现重复三元组）。

代码：

1. 暴力解法

//三数之和暴力解法
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> ret;sort(nums.begin(), nums.end());int n = nums.size();for (int i = 0; i < n; ){for (int j = i + 1; j < n; ){for (int k = j + 1; k < n;  ){if (nums[i] + nums[j] + nums[k] == 0)ret.push_back({ nums[i],nums[j],nums[k] });k++;while (k < n && nums[k] == nums[k - 1])k++;}j++;while (j < n && nums[j] == nums[j - 1])j++;}i++;while (i < n && nums[i] == nums[i - 1])i++;}return ret;}
};

2. 优化方法：双指针（左右指针）策略（利用单调性）

//三数之和优化解法
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> ret;sort(nums.begin(), nums.end());int n = nums.size();for (int i = 0; i < n; ){if (nums[i] > 0)break;int left = i + 1, right = n - 1;while (left < right){if (nums[left] + nums[right] == -nums[i]){ret.push_back({ nums[left], nums[right], nums[i] });left++;right--;while (left < right && nums[left] == nums[left-1])left++;while (left < right && nums[right] == nums[right+1])right--;}else if (nums[left] + nums[right] < -nums[i]){left++;}else {right--;}}i++;while(i < n && nums[i] == nums[i-1])i++;}return ret;}
}

题目8：四数之和

链接：18. 四数之和 - 力扣（LeetCode）

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按 任意顺序 返回答案。

核心思路：

1. 暴力解法

先对数组排序（为去重做准备）；枚举所有可能的四元组(i, j, k, z)，要求i < j < k < z，判断nums[i] + nums[j] + nums[k] + nums[z] == target；若符合条件，将四元组加入结果集，同时通过跳过重复元素（相同值的a、b、c、d）避免重复四元组。

但是四层循环的时间复杂度为O(n⁴)，在数组长度较大时运算量极大，无法满足时间要求。

2. 优化方法：双指针（左右指针）策略（利用单调性）

利用排序后的单调性，通过 “固定两个数 + 双指针找剩余两个数” 的方式，将四层循环降为三层，时间复杂度优化至O(n³)，同时通过多层去重确保结果唯一。

步骤：

1. 排序预处理：对数组升序排序。排序的作用：一是使重复元素相邻，便于后续去重；二是为双指针移动提供单调性基础，减少无效判断。
2. 固定前两个数：

第一层循环固定第一个数nums[i]（i从 0 开始），若i > 0且nums[i] == nums[i-1]，则跳过当前i（去重，避免重复四元组）；
第二层循环固定第二个数nums[j]（j从i+1开始），若j > i+1且nums[j] == nums[j-1]，则跳过当前j（进一步去重）。

3. 双指针找剩余两数：在j右侧的子数组[j+1, n-1]中，用左指针left = j+1、右指针right = n-1寻找满足nums[left] + nums[right] == target - nums[i] - nums[j]的组合：

若nums[left] + nums[right] < 目标剩余和（即target - nums[i] - nums[j]）：需增大两数之和，将left右移（利用升序特性，右侧数更大）；
若nums[left] + nums[right] > 目标剩余和：需减小两数之和，将right左移；
若nums[left] + nums[right] == 目标剩余和：找到有效四元组，加入结果集，随后同时将left右移、right左移，并跳过所有与当前left、right相同的元素（双指针去重，避免同一i、j下出现重复四元组）。

代码：

1. 暴力解法

1//四数之和暴力解法
class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> ret;sort(nums.begin(), nums.end());int n = nums.size();for (int i = 0; i < n; i++){for (int j = i + 1; j < n; j++){for (int k = j + 1; k < n; k++){for (int z = k + 1; z < n; z++){if (nums[i] + nums[j] + nums[k] + nums[z] == target){ret.push_back({ nums[i],nums[j],nums[k],nums[z] });}}}}}return ret;}
};

2. 优化方法：双指针（左右指针）策略（利用单调性）

//四数之和优化解法
class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> v;sort(nums.begin(), nums.end());int n = nums.size();for (int i = 0; i < n; ){for (int j = i + 1; j < n; ){int left = j + 1, right = n - 1;long long aim = (long long)target - nums[i] - nums[j];while (left < right){if (nums[left] + nums[right] == aim){v.push_back({ nums[i], nums[j], nums[left], nums[right] });left++;right--;while (left < right && nums[left] == nums[left - 1])left++;while (left < right && nums[right] == nums[right + 1])right--;}else if (nums[left] + nums[right] < aim)left++;elseright--;}j++;while (j < n && nums[j] == nums[j - 1])j++;}i++;while (i < n && nums[i] == nums[i - 1])i++;}return v;}
};