当前位置：首页 > news >正文

软件设计师备考-（十六）数据结构及算法应用（重要）

news 2025/9/9 6:53:06

16.1 前言

16.2 分治法

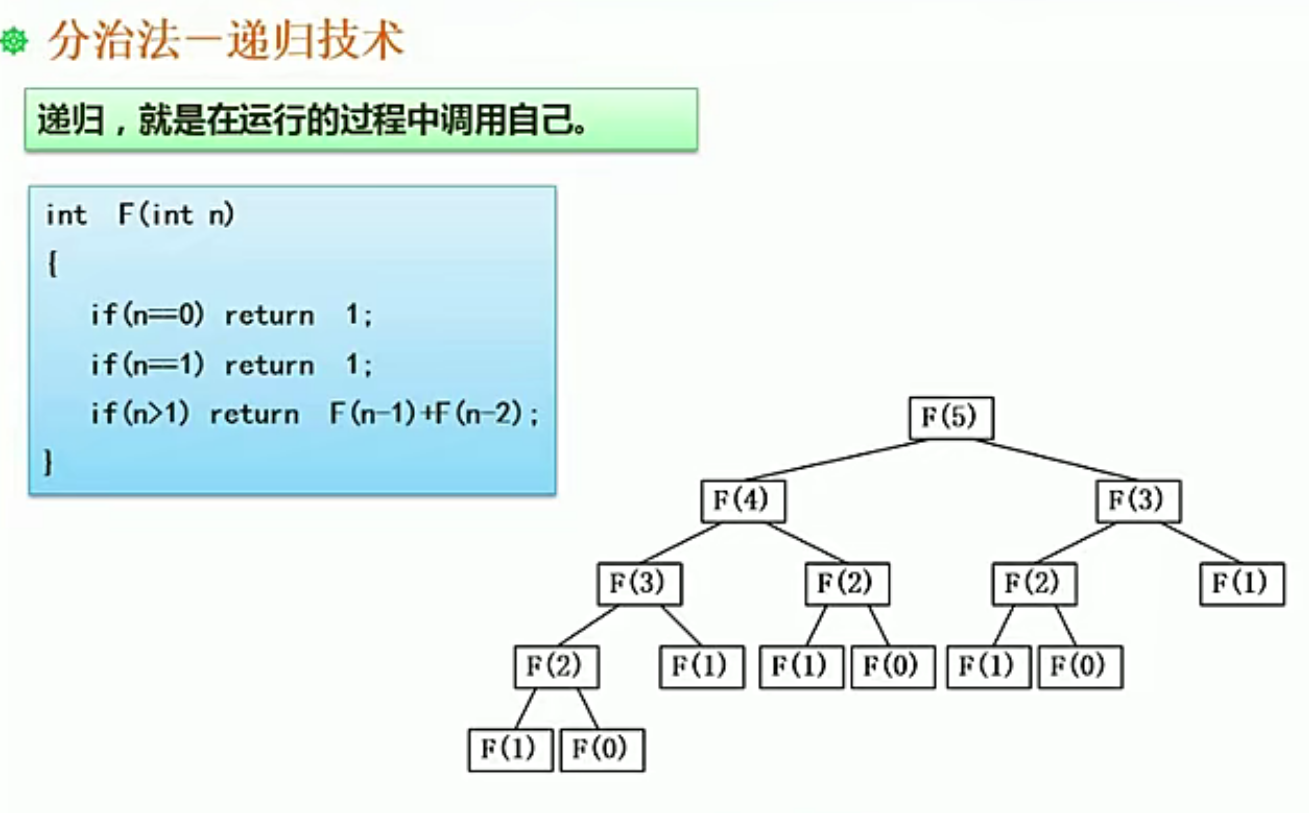
16.3 分治法（递归技术）

16.4 分治法（二分查找法）

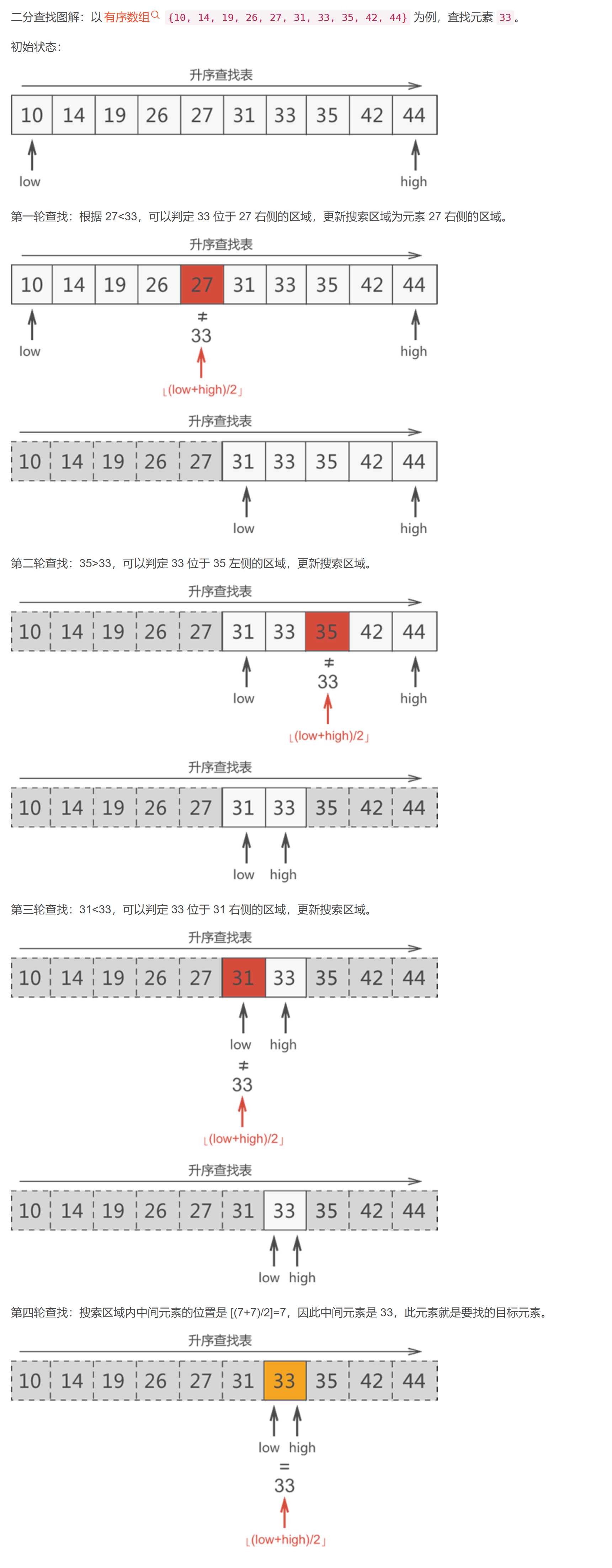
二分法：二分查找算法是一种在有序数组中查找某一特定元素的搜索算法，其思想就是不断地将有序查找表“一分为二”，逐渐缩小搜索区域，进而找到目标元素。
搜素过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；
如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。
小于中间元素m：high = m-1
大于中间元素m：low = m+1
如果在某一步骤数组为空，则代表找不到。
这种搜索算法每一次比较都使搜索范围缩小一半。折半搜索每次把搜索区域减少一半，时间复杂度为Ο(logn)
注：使用二分查找的前提条件是，数组已经是有序的

伪代码举例：

L：可以理解为数组
m：就是中间元素的下标
a：开始下标（左、low）
b：结束下标（右，hign）
x：查找的值

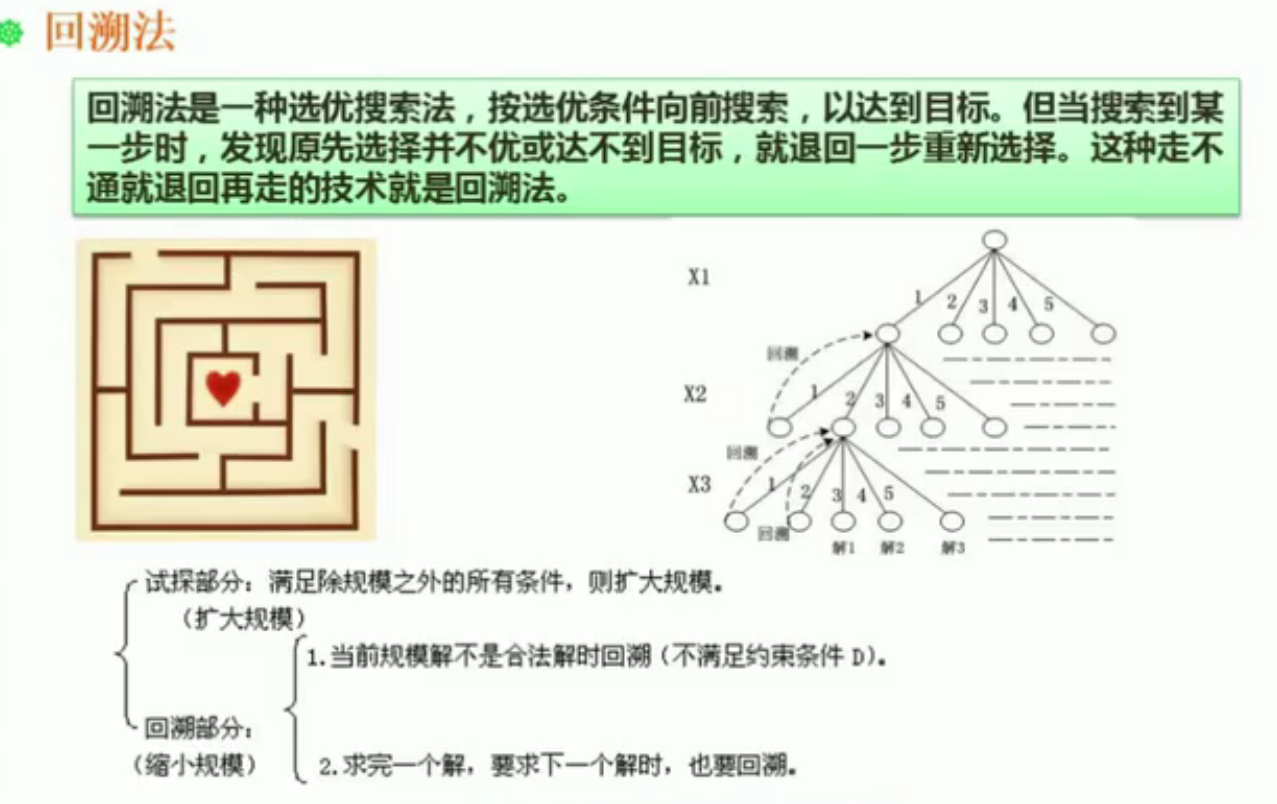
16.5 回溯法

16.6 贪心法

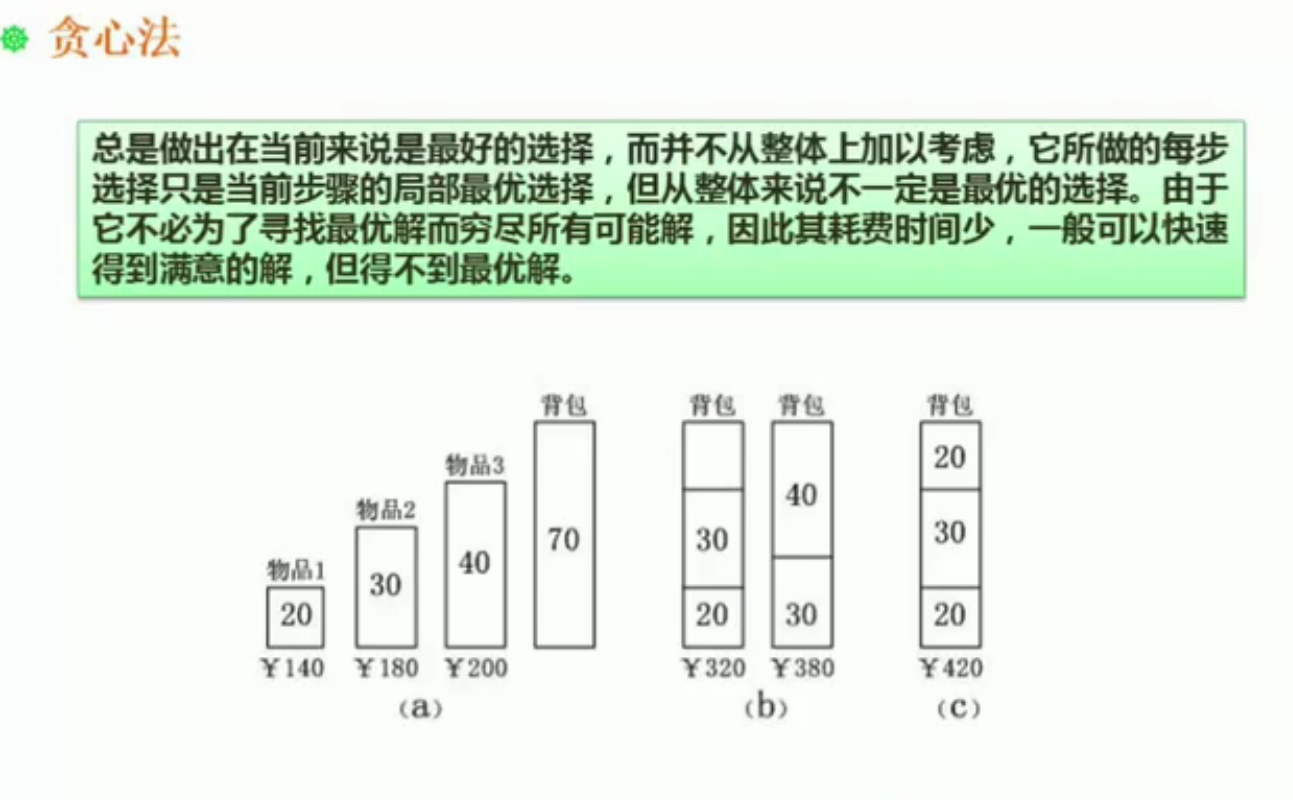
贪心法最经典的示例：解决背包问题
下图中，假设背包的贪心算法的规定是：每10体积的价值最优
那么物品1每10体积价值：70
物品2每10体积价值：60
物品3每10体积价值：50
贪心算法就会将物品以，物品1—》物品2—》物品3的顺序放入
当开始放物品3的时候发现背包容量不足，就停止放入
关于背包问题，需要注意的事项：
物体唯不唯一（一个物体只有一个，只能放一个到背包中【零一背包问题】）
物体如果可以重复放的话，那最优解结果又不一样了

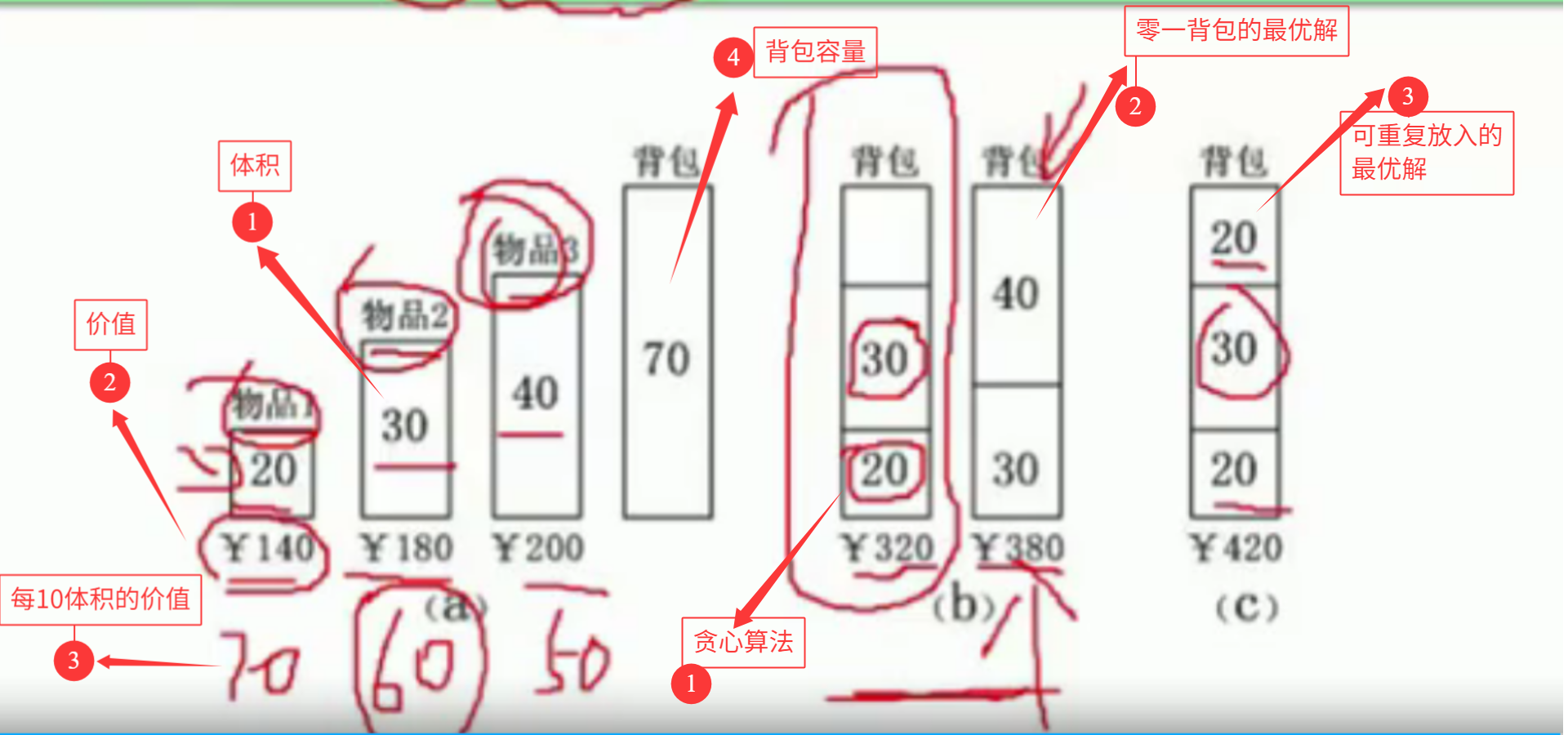
判断是否使用了贪心算法：每一步结果使用最优，但是最终结果不一定是最优解

16.7 动态规划法

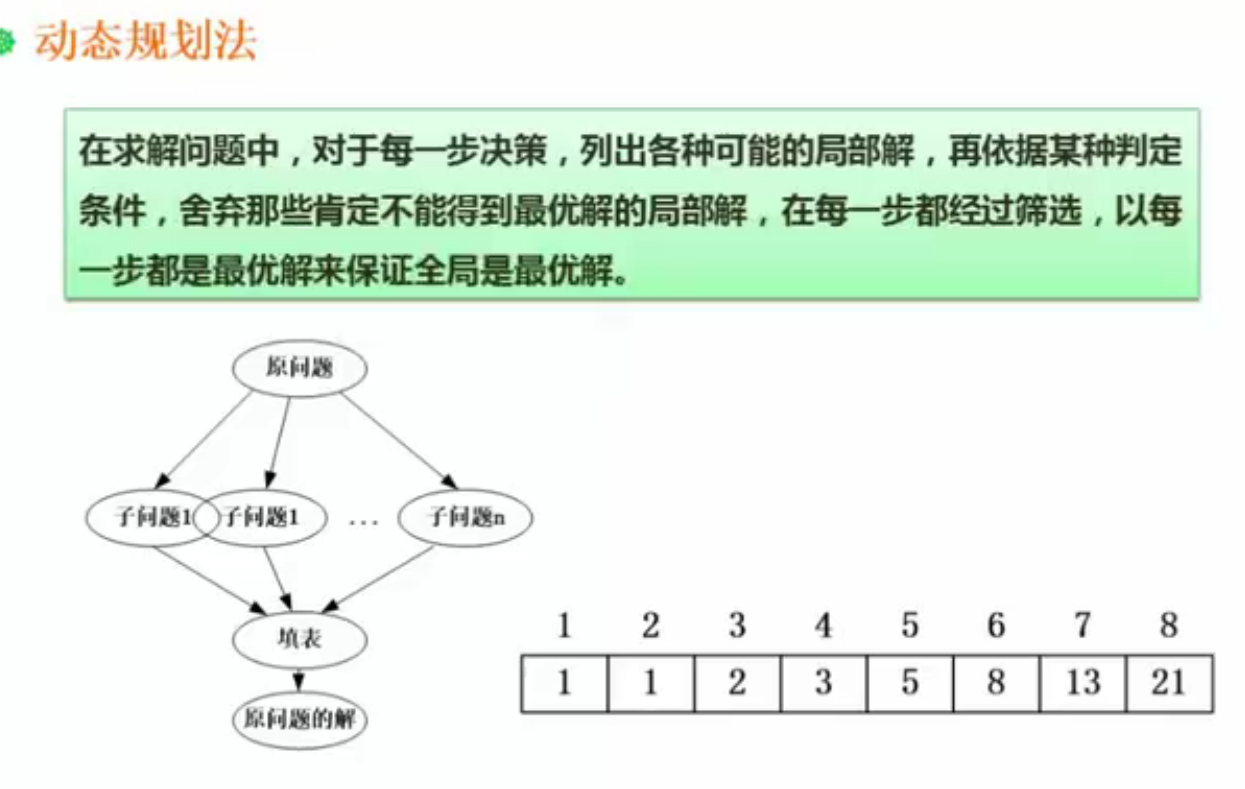
动态规划法的特点是会创建一个表，进行填表

16.8 数据结构及算法应用案例分析1

问题一：
- （1）j = 0
  - 由代码中可知，没有给j初始化赋值，所以这里的代码应该是j=0，初始化j的下标
- （2）b[j] = b[j]+s[i]
  - s：表示货物的体积
  - b：表示集装箱当前已经装入货物的体积
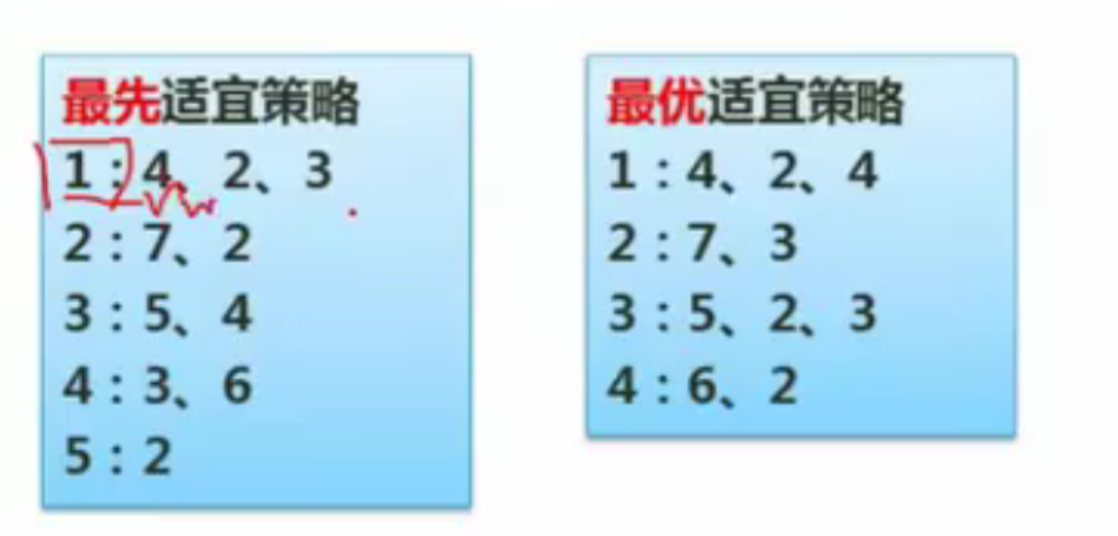
  - 由题可知，最先适宜策略，是每次将一个货物装入第一个能够容纳它的集装箱中。
  - b(当前下标集装箱已经装入货物的体积) = s(当前下标货物的体积) + b(当前下标集装箱已经装入货物的体积)
- （3）min = temp
  - 由题可知，最优适宜策略，总是把货物装到能容纳它，且目前剩余容量最小的集装箱【其实可以理解为，合理利用每一点资源，最佳利用资源】
  - temp = C - b[j] - s[i]，表示集装箱容量-当前下标位置的货物的体积-当前下标已经装入货物的体积 = 剩余的体积
  - min = temp，题中说min表示当前所用集装箱装入货物后的最小剩余容量，起始就是上述计算出来的temp
- （4）b[m] = b[m]+s[i]
  - 根据题可知，我们在计算出，temp的时候，下面给m = j ，赋了一个值，这个值就表示，当前容量最小且能容下物品的集装箱的下标位置。
  - 下面就要将物品添加到集装箱中，b[m] = b[m]+s[i]，b当前集装箱的装入货物的体积 = b当前集装箱的装入货物的体积 + s所要添加货物的体积

问题二：
（5）、（6）贪心法
（7）、（8）都是 o（n*n）——o（n²），双层for循环

问题三：
由题可知，n=10表示有10个货物
C=10，表示集装箱的容量为10
最优：先从剩余量最小的箱子匹配
最先：第一个可以容纳货物容量的
（9）5、（10）4
（11）否，因为无论是最先适宜策略，还是最优适宜策略，都是贪心算法，它只保证每一步是最优解，但并不保证整体能够达到最优解。

16.9 数据结构及算法应用案例分析2

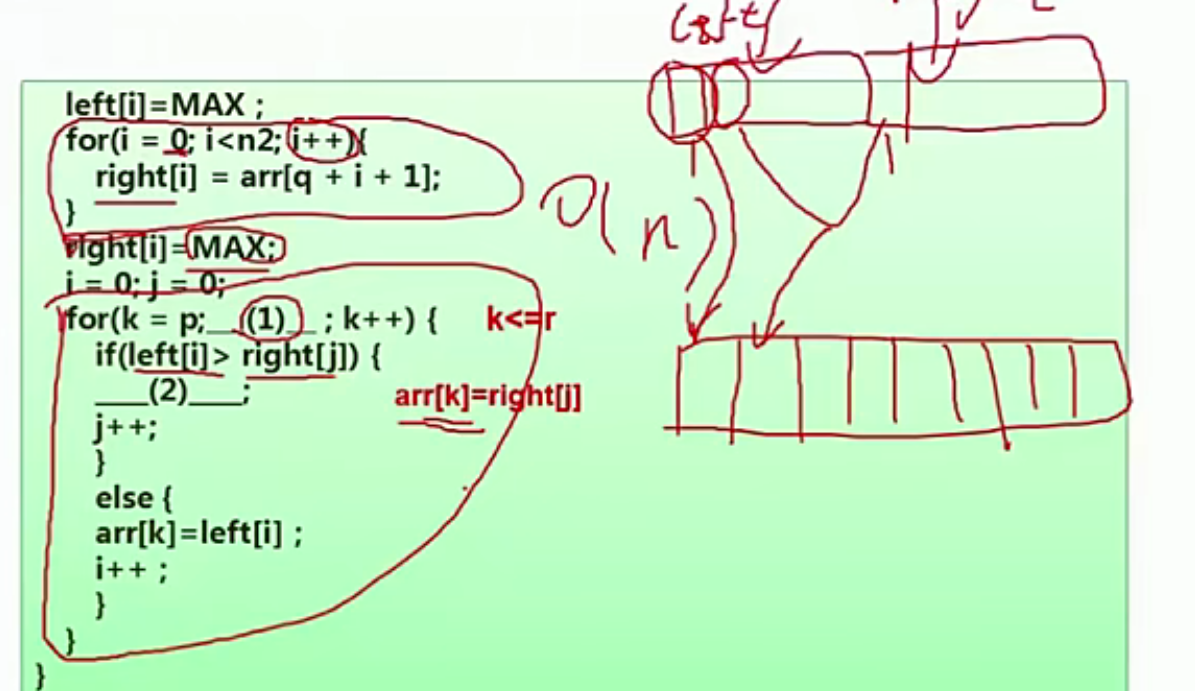
（5）分治
由题可知，采用归并排序，将元素分成n/2个子元素，然后用归并排序对俩个子数组进行递归排序，最后再进行合并2个子数组【符合分治算法的理念，分解——解决——合并】
（6）T（n） = 2T（n/2）+O（n）
假设时间为T（n）的话，那么分治，解决俩个子问题（mergeSort），一个就为T（n/2），俩个就为2T（n/2）
下面还有一个归并，merge(arr,begin,,mid,end)，通过代码发现，归并，最多都是单程循环，所以时间复杂度为O（n）
T（n） = 2T（n/2）+O（n）
（7）O(n log n)
（8）O（n）
空间复杂度：我们需要的空间有多少个，就有多少的交换空间
（9）n1+n2
分治后n1与n2已经排好序了，然后进行归并，其实就是n1的每个数据与n2的每个数据一一比较，最终是n1+n2