讲解一下冒泡排序
问题
讲解一下冒泡排序
我的回答
冒泡排序其实是最基础的排序算法之一,它的名字很形象,就像水里的气泡往上冒一样,大的元素会慢慢"冒"到数组的后面。
基本思路是这样的:
我们每次都比较相邻的两个元素,如果前面的比后面的大,就把它们交换位置。这样一轮下来,最大的元素就会被"冒"到最后面。然后我们再重复这个过程,第二大的元素就会到倒数第二的位置,以此类推。
具体步骤:
- 从第一个元素开始,比较相邻的两个元素
- 如果左边比右边大,就交换它们
- 继续向右比较,直到这一轮结束
- 重复上面的过程,但每次可以少比较一个元素
假设我们要排序数组:[5, 2, 8, 1, 9]
第一轮冒泡:
- 比较 5 和 2:5 > 2,交换 → [2, 5, 8, 1, 9]
- 比较 5 和 8:5 < 8,不交换 → [2, 5, 8, 1, 9]
- 比较 8 和 1:8 > 1,交换 → [2, 5, 1, 8, 9]
- 比较 8 和 9:8 < 9,不交换 → [2, 5, 1, 8, 9]
第一轮结束,最大的数 9 已经"冒"到最后了。
第二轮冒泡:
- 比较 2 和 5:2 < 5,不交换 → [2, 5, 1, 8, 9]
- 比较 5 和 1:5 > 1,交换 → [2, 1, 5, 8, 9]
- 比较 5 和 8:5 < 8,不交换 → [2, 1, 5, 8, 9]
第二轮结束,第二大的数 8 到了倒数第二位。
第三轮冒泡:
- 比较 2 和 1:2 > 1,交换 → [1, 2, 5, 8, 9]
- 比较 2 和 5:2 < 5,不交换 → [1, 2, 5, 8, 9]
第四轮冒泡:
- 比较 1 和 2:1 < 2,不交换 → [1, 2, 5, 8, 9]
最终结果:[1, 2, 5, 8, 9]
就像气泡一样,每一轮都有一个最大的数"冒"到它应该在的位置,这就是冒泡排序名字的由来!
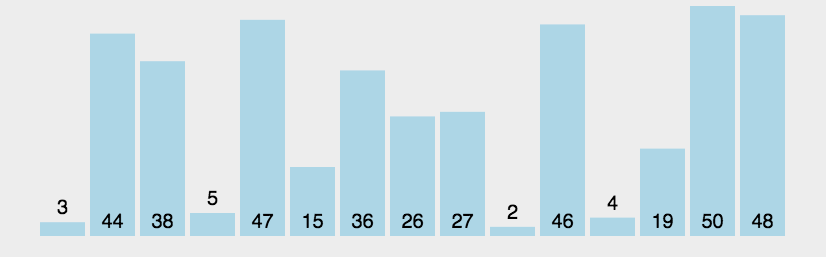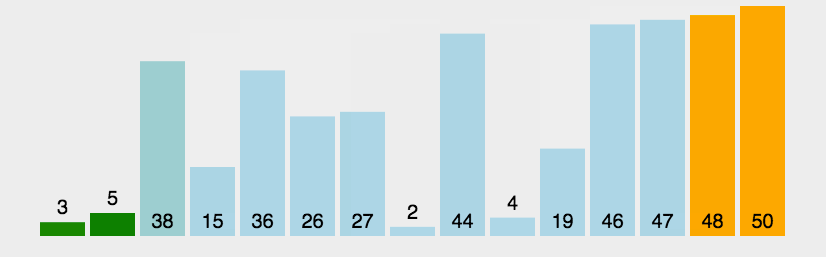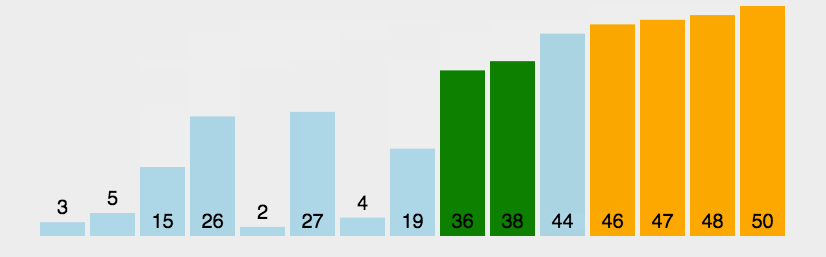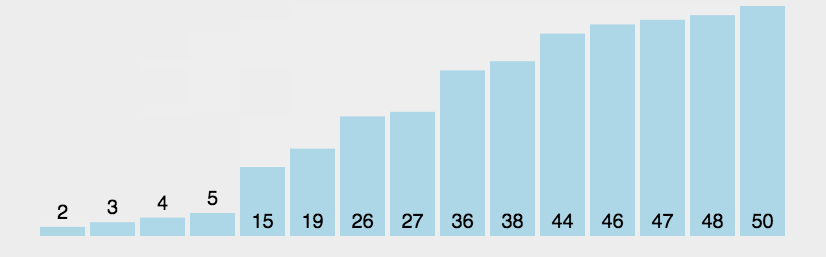
时间复杂度是O(n²),因为有两层循环。最好情况下如果数组已经有序,我们可以优化到O(n)。空间复杂度是O(1),因为只用了常数级别的额外空间。
#include <iostream>
#include<vector>
void bubbleSort(std::vector<int>& nums)
{int start = nums[0];int n = nums.size();for (int i = 0; i < n; i++){for (int j = 0; j < n - i-1; j++){if (nums[j] > nums[j+1]){std::swap(nums[j], nums[j + 1]);}}}
}int main()
{std::vector<int> nums = { 5,2,1,6,4,8 };bubbleSort(nums);for (auto& num : nums){std::cout << num << std::endl;}return 0;
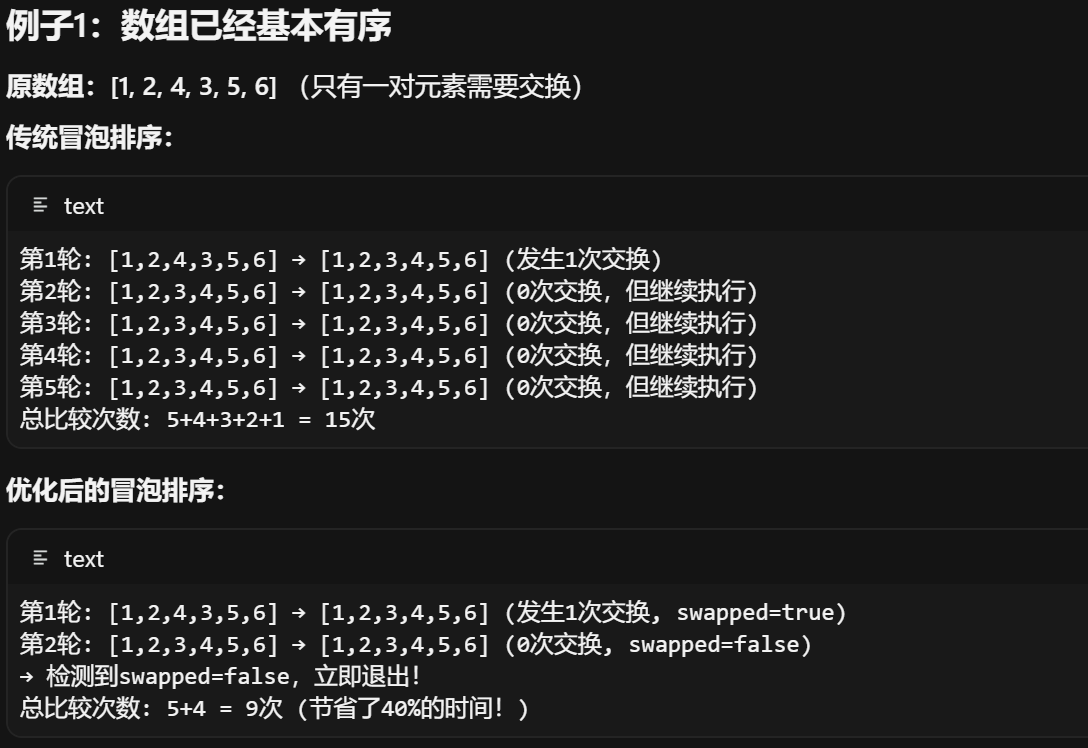
}这个代码可以优化,优化的逻辑就是:如果某一轮没有发生交换,说明数组已经有序,可以提前结束
比如说
void bubbleSort(std::vector<int>& nums)
{int n = nums.size();for (int i = 0; i < n - 1; i++){bool swapped = false; // 标记这一轮是否发生交换for (int j = 0; j < n - i - 1; j++){if (nums[j] > nums[j + 1]){std::swap(nums[j], nums[j + 1]);swapped = true;}}if (!swapped) break; // 如果没有交换,提前退出}
}