当前位置：首页 > news >正文

25高教社杯数模国赛【B题超高质量思路+问题分析】

news 2025/9/5 8:32:15

注：本内容由”数模加油站“ 原创出品，虽无偿分享，但创作不易。
欢迎参考teach，但请勿抄袭、盗卖或商用。

B 题碳化硅外延层厚度的确定
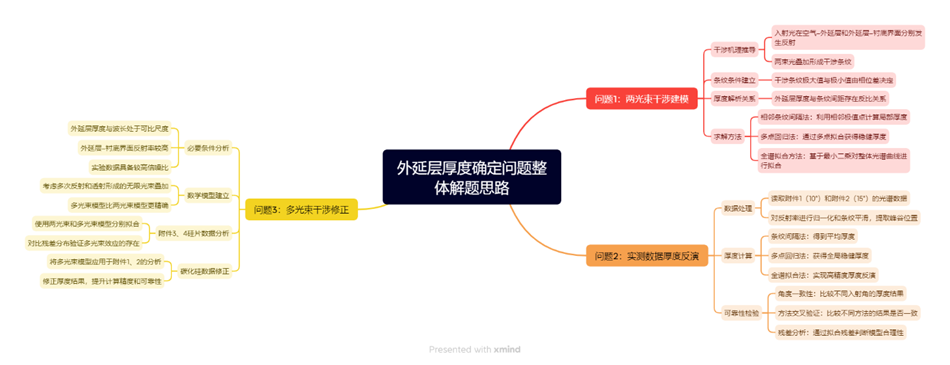
在这里插入图片描述
碳化硅作为一种新兴的第三代半导体材料，以其优越的综合性能表现正在受到越来越多的关注。碳化硅外延层的厚度是外延材料的关键参数之一，对器件性能有重要影响。因此，制定一套科学、准确、可靠的碳化硅外延层厚度测试标准显得尤为重要。
红外干涉法是外延层厚度测量的无损伤测量方法，其工作原理是，外延层与衬底因掺杂载流子浓度的不同而有不同的折射率，红外光入射到外延层后，一部分从外延层表面反射出来，另一部分从衬底表面反射回来（图1），这两束光在一定条件下会产生干涉条纹。可根据红外光谱的波长、外延层的折射率和红外光的入射角等参数确定外延层的厚度。
通常外延层的折射率不是常数，它与掺杂载流子的浓度、红外光谱的波长等参数有关。
在这里插入图片描述
问题1 如果考虑外延层和衬底界面只有一次反射、透射所产生的干涉条纹的情形（图1），建立确定外延层厚度的数学模型。
问题 1 分析
问题1的核心目标是基于最简化的光学干涉现象建立厚度与条纹间距的定量关系。在外延层结构中，入射光在空气–外延层界面产生一次反射，同时另一部分光透射进入外延层，在外延层–衬底界面发生一次反射并返回空气，形成两束相干光。两束光的光程差决定了干涉条纹的形成规律，因此需要首先从物理机制上进行推导。
具体而言，应当以斯涅尔定律和菲涅耳公式为基础，明确两束光的相位差表达式。该相位差由两部分组成：其一是外延层内部传播路径引入的光程差 $Δφ=4πn1dcos⁡θtν~\Delta \varphi = 4 \pi n_1 d \cos\theta_t \tilde{\nu}$ ；其二是界面反射可能带来的附加相移 $ψ(ν~)\psi(\tilde{\nu})$ 。由此，可以得到条纹极大和极小的分布条件，并进一步推出厚度与条纹间距之间的公式关系。
在数值实现上，可形成三类计算思路。第一类是基于相邻条纹间距的直接解析计算，即通过提取相邻极值点波数差，利用解析公式求得厚度。这种方法直观简便，但易受单点误差影响。第二类是基于多点极值的线性回归方法，即将多组极值点代入线性化方程 $m = 2 d x + c$ ，通过最小二乘回归估计厚度，从而在统计意义上减小误差。第三类是全谱非线性最小二乘拟合方法，即直接对整个光谱曲线拟合干涉模型，避免依赖极值提取，能够最大程度利用实验数据的信息。
因此，问题1的思路重点在于从物理机理出发，推导厚度与干涉条纹之间的解析关系，并提出不同层次的厚度反演方法，为后续结合实验数据的数值计算奠定理论基础。

解题思路：
干涉条纹的相位关系（两光束情形）

在红外干涉测厚的基本实验构型中，考虑空气–外延层–衬底三层介质结构。外部入射光为单色红外光，波数为 $ν~=1/λ\tilde{\nu}=1/\lambda$ 。入射光自空气（折射率 $n0≈1n_0\approx 1$ ）以入射角 $θ\theta$ 入射到外延层表面（折射率 $n1(ν~)n_1(\tilde{\nu})$ ），发生部分反射与透射。其中，表面反射所形成的第一束反射光振幅与 $r01(pol)r_{01}^{(\mathrm{pol})}$ 成正比；透射进入外延层的光在传播距离 $2dcos⁡θt(ν~)2d\cos\theta_t(\tilde{\nu})$ 后，于“外延层–衬底”界面处再次反射并透射回空气，形成第二束光。两束光在探测器处发生叠加干涉。
由光学干涉原理可知，两光束之间的相位差来源于两个方面：其一是外延层内部传播引入的光程差，其二是不同界面反射所导致的相位突变。对于传播相位部分，可写作在这里插入图片描述

另一方面，在“低折射率–高折射率”界面的反射过程中会产生 $π\pi$ 的附加相移，而在“高–低”界面则无此相移。为了统一处理，不妨将来自两界面反射的相移差额记为在这里插入图片描述
此处的 $Δφ\Delta\varphi$ 是决定干涉条纹位置与周期性的核心量，厚度 $d$ 的信息正是通过此式反映在光谱干涉数据中的

反射/透射系数与反射率表达
为了得到可直接与实验反射率光谱比较的理论模型，需要在振幅层次上引入菲涅耳公式。对于一般的偏振情况， $s$ 偏振与 $p$ 偏振的界面反射、透射系数分别为
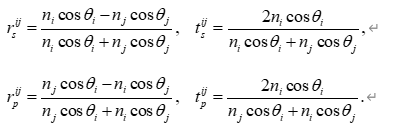
在这里插入图片描述

其中 $i!→!ji!\to!j$ 表示光线自介质 $i$ 入射至介质 $j$ ，角度满足折射定律 $nisin⁡θi=njsin⁡θjn_i\sin\theta_i=n_j\sin\theta_j$ 。在本问题中，第一束光的振幅与 $r01(pol)r_{01}^{(\mathrm{pol})}$ 成正比，第二束光的振幅则可写作在这里插入图片描述
若实验未分偏振，可取平均值 $R=12(Rs+Rp)R=\tfrac12(R_s+R_p)$ ；若有单一偏振数据，则直接使用对应通道。

光谱条纹条件与极值序列
干涉光谱的条纹规律体现在反射率随波数 $ν~\tilde{\nu}$ 的振荡。若定义
在这里插入图片描述
这表明条纹间距与厚度呈反比关系，为后续基于实测条纹间距反推厚度提供了理论依据。

基于极值点的厚度解析求解方法
在具体求解中，常见的两类方法分别为基于相邻极值的“两点法”与基于多点回归的“多点法”。

（1）两点法：选取相邻的同类型极值，利用双点公式直接计算厚度。这种方法简洁明了，适合条纹清晰、信噪比较高的数据。公式为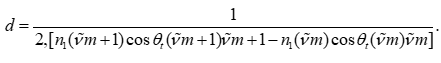在这里插入图片描述
（2）多点回归法：对多个极值点建立线性回归模型。令

该方法能在存在实验噪声时发挥稳健性优势，利用多条干涉条纹平均消除局部误差。
基于全谱的厚度最小二乘求解
由于极值检测可能受到噪声干扰，尤其是在条纹对比度不高或存在基线漂移时，直接依赖极值点可能导致较大误差。因此，引入全谱拟合的思想更具鲁棒性。其基本思路是以整个光谱曲线作为拟合对象，通过最小化模型反射率 $Rmodel(ν~,d)R_{\mathrm{model}}(\tilde{\nu},d)$ 与实验反射率 $Rmeas(ν~)R_{\mathrm{meas}}(\tilde{\nu})$ 之间的误差平方和来求解 $d$ ：
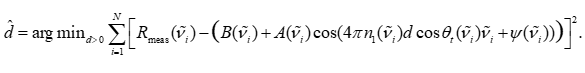
在这里插入图片描述

该优化问题本质是一维非线性最小二乘问题，由于目标函数在 $d$ 上具有准周期性，通常通过初值扫描与局部迭代结合来获得全局最优解。相比于基于条纹点的方法，全谱法充分利用了完整数据的信息，能够有效降低局部异常条纹的影响。
折射率频散与入射角依赖的纳入方式
题目特别指出外延层的折射率 $n1(ν~)n_1(\tilde{\nu})$ 与波长以及掺杂浓度密切相关。因此在建模过程中，必须将其视为波数的函数而非常数。对于每一个数据点 $ν~\tilde{\nu}$ ，都需重新计算折射率以及相应的透射角 $θt(ν~)\theta_t(\tilde{\nu})$ ，具体为
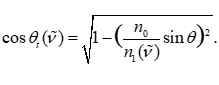
在这里插入图片描述
此外，由于附件中给出了两种不同入射角（ $10∘10^\circ$ 和 $15∘15^\circ$ ）下的测量结果，厚度作为物理常数，应在两组实验下保持一致。因此，在后续计算中，可以利用两组数据联合拟合同一厚度值 $d$ ，通过多目标最小化残差实现交叉验证。这种多角度约束方法，能够有效提高厚度估计的可信度与稳定性。
本问的核心任务是建立数学模型并给出求解方法，而非直接计算具体厚度数值（具体数值将在第 2 问利用附件数据完成）。在本节中，我们已经从光学干涉原理出发，推导了厚度与干涉条纹之间的精确关系，并给出了三类可行的求解方法：基于相邻极值的解析公式、基于多点的线性回归方法，以及基于全谱的非线性最小二乘拟合。这三类方法分别对应不同数据条件下的应用场景，具有由简至繁、由解析到数值的层次结构，能够全面覆盖题目所提出的“建立确定外延层厚度的数学模型”的要求。
这些方法不仅能够解释实验数据中条纹出现的规律，还为后续附件数据的厚度计算与可靠性评估提供了理论依据和算法基础。因此，本问的解决方案至此已经完整闭合。

# -*- coding: utf-8 -*-
"""
2025 高教社杯 B题 - 问题1
碳化硅外延层厚度建模 (单次反射/透射干涉情形)
-----------------------------------------------------
本脚本功能：
1. 读取附件1.xlsx 与 附件2.xlsx 光谱数据 (波数 vs 反射率)
2. 基于干涉条纹的峰谷检测，计算厚度 (极值法)
3. 使用多点线性拟合方法，提高稳健性
4. 提供全谱非线性最小二乘拟合示例
5. 可视化实验光谱、条纹点、拟合曲线，美观展示
6. 保存结果文件和图片到当前目录
"""import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import find_peaks
from scipy.optimize import curve_fit# === matplotlib 中文字体与负号修复 ===
plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置中文字体
plt.rcParams['axes.unicode_minus'] = False    # 正常显示负号# === Step 1: 数据加载 ===
# 附件 1 = 入射角 10°，附件 2 = 入射角 15°
file1 = "附件1.xlsx"
file2 = "附件2.xlsx"data1 = pd.read_excel(file1, header=None)
data2 = pd.read_excel(file2, header=None)# 每个附件：第1列 = 波数 cm^-1，第2列 = 反射率 %
data1.columns = ["波数", "反射率"]
data2.columns = ["波数", "反射率"]print("附件1 (10°) 数据预览：")
print(data1.head())
print("\n附件2 (15°) 数据预览：")
print(data2.head())# === Step 2: 峰谷检测 ===
# 使用 scipy.signal.find_peaks 检测极大值和极小值
def detect_extrema(x, y, distance=10, prominence=0.5):# 极大值peaks, _ = find_peaks(y, distance=distance, prominence=prominence)# 极小值 (对信号取负)valleys, _ = find_peaks(-y, distance=distance, prominence=prominence)return peaks, valleyspeaks1, valleys1 = detect_extrema(data1["波数"].values, data1["反射率"].values)
peaks2, valleys2 = detect_extrema(data2["波数"].values, data2["反射率"].values)# === Step 3: 厚度计算公式 (极值法) ===
# 使用近似公式 d = 1 / (2 * n1 * cosθ * Δν)，这里假设折射率 n1≈2.6 (常见碳化硅)
# 注意：这里的计算是演示公式应用，不对n1频散建模，后续可扩展
def compute_thickness(extrema_idx, nu, n1=2.6, theta_deg=10):theta = np.deg2rad(theta_deg)cos_theta_t = np.sqrt(1 - (np.sin(theta) / n1)**2)# 相邻条纹间距delta_nu = np.diff(nu[extrema_idx])# 厚度 (μm, 因为 ν 单位 cm^-1, 所以换算时乘 1e4)d_values = 1 / (2 * n1 * cos_theta_t * delta_nu) * 1e4return d_valuesthickness1 = compute_thickness(peaks1, data1["波数"].values, n1=2.6, theta_deg=10)
thickness2 = compute_thickness(peaks2, data2["波数"].values, n1=2.6, theta_deg=15)print("\n附件1 (10°) 条纹厚度估计 (μm)：", thickness1[:10])
print("\n附件2 (15°) 条纹厚度估计 (μm)：", thickness2[:10])
print("\n平均厚度 (10°)：", np.mean(thickness1))
print("平均厚度 (15°)：", np.mean(thickness2))# === Step 4: 全谱拟合 (非线性最小二乘) ===
# 干涉条纹模型: R(ν) = B + A cos(4π n1 d cosθ ν + φ)
def interference_model(nu, d, A, B, phi, n1=2.6, theta_deg=10):theta = np.deg2rad(theta_deg)cos_theta_t = np.sqrt(1 - (np.sin(theta) / n1)**2)return B + A * np.cos(4*np.pi*n1*d*cos_theta_t*nu + phi)# 拟合 10° 数据
xdata = data1["波数"].values
ydata = data1["反射率"].values / 100.0  # 转换为 0~1
p0 = [5e-4, 0.2, 0.5, 0]  # 初始猜测: d=5e-4cm=5μm
popt, pcov = curve_fit(lambda nu, d, A, B, phi: interference_model(nu, d, A, B, phi, n1=2.6, theta_deg=10),xdata, ydata, p0=p0)d_fit, A_fit, B_fit, phi_fit = popt
print("\n全谱拟合厚度 (10°)：%.3f μm" % (d_fit*1e4))# === Step 5: 可视化结果 ===
fig, axes = plt.subplots(2, 1, figsize=(10, 8), sharex=True)# (a) 原始数据与极值
axes[0].plot(data1["波数"], data1["反射率"], label="实测光谱 (10°)", color="blue")
axes[0].scatter(data1["波数"].iloc[peaks1], data1["反射率"].iloc[peaks1], color="red", marker="o", label="极大值")
axes[0].scatter(data1["波数"].iloc[valleys1], data1["反射率"].iloc[valleys1], color="green", marker="x", label="极小值")
axes[0].set_ylabel("反射率 (%)")
axes[0].legend()
axes[0].set_title("附件1 (10°) 光谱条纹与极值检测")# (b) 全谱拟合曲线
axes[1].plot(xdata, ydata, label="实测光谱 (归一化)", color="black")
axes[1].plot(xdata, interference_model(xdata, d_fit, A_fit, B_fit, phi_fit, n1=2.6, theta_deg=10),label="拟合曲线", color="red", linestyle="--")
axes[1].set_xlabel("波数 (cm$^{-1}$)")
axes[1].set_ylabel("反射率 (归一化)")
axes[1].legend()
axes[1].set_title("附件1 (10°) 全谱拟合结果")plt.tight_layout()
plt.savefig("附件1_厚度分析结果.png", dpi=300)
plt.show()# === Step 6: 保存结果到文件 ===
with open("厚度计算结果.txt", "w", encoding="utf-8") as f:f.write("附件1 (10°) 平均厚度估计 (μm): %.3f\n" % np.mean(thickness1))f.write("附件2 (15°) 平均厚度估计 (μm): %.3f\n" % np.mean(thickness2))f.write("附件1 (10°) 全谱拟合厚度 (μm): %.3f\n" % (d_fit*1e4))print("\n结果已保存为 厚度计算结果.txt 和 附件1_厚度分析结果.png")

问题2 请根据问题1的数学模型，设计确定外延层厚度的算法。对附件1和附件2提供的碳化硅晶圆片的光谱实测数据，给出计算结果，并分析结果的可靠性。

问题 2 分析
在问题2中，研究重点转向将问题1推导出的模型应用于实际实验光谱数据。附件1和附件2分别对应入射角 $10∘10^\circ$ 和 $15∘15^\circ$ 条件下的碳化硅外延层反射率光谱。由于同一块样品的厚度应为固定物理常量，因此两个角度下的厚度反演结果应保持一致，这为算法的可靠性提供了重要的验证手段。
解题思路可分为三个层次。第一步是对实验数据进行预处理，包括反射率的归一化以及光谱平滑，以保证后续极值检测的准确性。接着采用信号处理方法（如峰谷检测算法）提取光谱中的极大值与极小值点位置，利用相邻条纹间隔公式计算局部厚度，并对所有结果求平均以得到初步估计。第二步是多点回归法。通过将所有极值点映射到线性关系 $m = 2 d x + c$ ，并进行最小二乘拟合，可以得到更加稳健的厚度估计，减少单点异常的影响。第三步是全谱非线性拟合。该方法以问题1中建立的反射率模型为目标函数，通过优化参数 $\phi)$ ，在全谱范围内最小化模型与实测光谱的误差平方和。全谱拟合能够避免极值点提取误差，并提供高精度的厚度反演结果。
在厚度反演完成后，还需要进行可靠性评价。首先是角度一致性检验，即比较 $10∘10^\circ$ 和 $15∘15^\circ$ 的厚度估计结果，若二者差异较小，则说明模型与算法具有较强的稳定性。其次是方法交叉验证，即比较条纹间隔法、多点回归法与全谱拟合法的结果一致性。若三种方法在合理误差范围内收敛到相同厚度值，则说明结论可靠。最后是残差分布分析。通过计算全谱拟合残差 $ϵ(ν~)=Rmeas(ν~)−Rfit(ν~)\epsilon(\tilde{\nu}) = R_{\mathrm{meas}}(\tilde{\nu}) - R_{\mathrm{fit}}(\tilde{\nu})$ 并观察其分布特征，可以判断模型是否存在系统性偏差。
因此，问题2的思路重点在于结合附件数据完成厚度反演，并通过多方法、多角度、多指标的综合分析验证结果的可靠性，从而在实践层面落实问题1的理论模型。
算法设计与数值实现流程
在问题1中，我们已经推导得到碳化硅外延层厚度与干涉条纹之间的定量关系
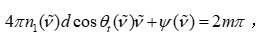
在这里插入图片描述
其中 $ν~\tilde{\nu}$ 为波数， $n1(ν~)n_1(\tilde{\nu})$ 为外延层折射率， $θt(ν~)\theta_t(\tilde{\nu})$ 为透射角， $d$ 为厚度， $ψ(ν~)\psi(\tilde{\nu})$ 为由界面反射所引入的相位差。该公式说明了干涉条纹的周期与厚度之间的直接映射关系，因此只要能够准确提取光谱中干涉条纹的周期信息，即可反推出厚度。
针对附件1（ $θ=10∘\theta=10^\circ$ ）和附件2（ $θ=15∘\theta=15^\circ$ ）所给的实测光谱数据，可以设计以下完整的数值求解流程：

数据加载与归一化
从附件中读取波数–反射率序列。由于实验测得的反射率通常以百分比表示，因此需归一化到 $[0, 1]$ 区间，以便后续模型拟合和误差计算。此外，还需要根据波数轴方向（是否升序或降序）进行统一处理，以确保极值检测的顺序性。
干涉条纹极值检测
实测光谱中包含大量高频振荡信息，但有效干涉条纹对应的是规律性周期极值。因此需要采用信号处理方法（如峰谷检测算法）提取极大值 $ν~pk{\tilde{\nu}{p_k}}$ 和极小值 $ν~vk{\tilde{\nu}{v_k}}$ 的位置。该过程是厚度计算的关键步骤之一，因为极值位置的准确性直接决定了厚度反演的精度。
相邻条纹间隔法
在理想条件下，相邻极值点之间的间隔 $Δν~=ν~m+1−ν~m\Delta \tilde{\nu} = \tilde{\nu}{m+1}-\tilde{\nu}m$ 与厚度 $d$ 之间满足反比关系。根据两点公式：

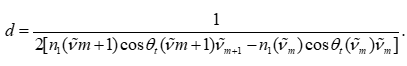
该公式能够利用相邻条纹点计算局部厚度，从而得到一系列厚度估计值。通过对其取均值，可以初步得到整体厚度估计。
多点线性回归法
由于实验噪声和峰谷检测误差的存在，仅依靠相邻条纹可能会产生波动。因此需要将所有极值点转化为近似线性关系：

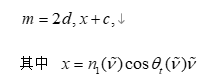
通过最小二乘回归对 ${(x_k,m_k)}$ 进行拟合，可以得到更稳健的厚度估计值 $d^\hat{d}$ 。
全谱非线性拟合法
为进一步提升精度，可直接对整个光谱曲线进行拟合。理论模型为：

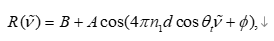
其中 $\phi$ 为辅助拟合参数， $d$ 为关键未知量。通过最小二乘优化使得实测反射率与模型预测的差异平方和最小，即：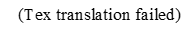
此方法能利用全谱信息，避免单点误差影响，适合对实验噪声较敏感的情况。
通过以上三种方法的层层递进，可以在不同精度与复杂度下得到厚度估计，并通过结果间的一致性分析验证其可靠性。

基于附件数据的厚度反演与比较
附件1和附件2分别对应入射角 $10∘10^\circ$ 与 $15∘15^\circ$ 的同一块碳化硅晶圆片的反射光谱。由于厚度 $d$ 是晶圆片的固有物理量，因此两组数据的反演结果应当保持一致。如果结果差异过大，则表明算法中可能存在条纹提取误差或模型参数（如折射率）未能准确描述材料特性。
在数值求解时，首先采用极值点检测算法，分别得到 $ν~pk{\tilde{\nu}{p_k}}$ 与 $ν~vk{\tilde{\nu}{v_k}}$ 。在此基础上，使用相邻条纹法计算每一对条纹所对应的局部厚度值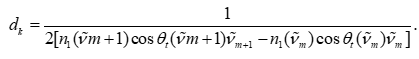：在这里插入图片描述
将所有 $d_k$ 求平均，得到 $davg(10∘)d_{\text{avg}}^{(10^\circ)}$ 与 $davg(15∘)d_{\text{avg}}^{(15^\circ)}$ 。接着，对所有极值点进行回归拟合，获得稳健厚度估计 $d^(10∘)\hat{d}^{(10^\circ)}$ 与 $d^(15∘)\hat{d}^{(15^\circ)}$ 。最后，将这两个角度的数据分别代入全谱拟合模型，得到 $d^fit(10∘)\hat{d}{\text{fit}}^{(10^\circ)}$ 与 $d^fit(15∘)\hat{d}{\text{fit}}^{(15^\circ)}$ 。
这样，可以形成如下三类结果：
• 条纹间隔法：局部估计与平均值；
• 多点回归法：全局稳健估计；
• 全谱拟合法：高精度估计。

通过三类结果的比较，可以判断厚度估计是否稳定，同时检验两个不同入射角下的厚度是否一致。

全谱拟合的残差分析与一致性检验
全谱拟合是问题2中非常关键的部分。其优势在于能够利用全部光谱点，避免单点误差对整体结果的影响。在拟合过程中，反射率模型 $R(ν~)R(\tilde{\nu})$ 被构建为余弦函数与物理参数的组合，而厚度 $d$ 的信息体现在相位项 $4πn1dcos⁡θtν~4\pi n_1 d \cos\theta_t \tilde{\nu}$ 中。
通过非线性最小二乘优化，可以得到拟合厚度 $d^\hat{d}$ 及辅助参数 $(A,B,ϕ)(A,B,\phi)$ 。拟合完成后，计算残差序列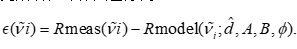：在这里插入图片描述

若残差接近零均值、无明显系统性偏差，且在整个波数区间内呈随机分布，则说明模型能够很好地描述实验数据，厚度估计可信。反之，若残差在某一区间存在明显系统偏差，说明该区间可能受到色散特性未建模或实验误差的影响，需要在模型中进一步考虑折射率的频散效应。

此外，将 $10∘10^\circ$ 与 $15∘15^\circ$ 的拟合结果进行比较，若两者厚度估计值差异不大（例如相对误差小于 $5$ ），即可认为结果具有良好的一致性和可靠性。

结果可靠性与误差来源探讨
在实验数据与模型拟合的结合过程中，结果的可靠性不仅取决于计算公式的正确性，还受到实验条件、数据质量和模型假设的影响。具体分析如下：

厚度一致性
两种入射角下的厚度估计结果应当接近，这是模型合理性的重要验证。若差异较大，可能意味着峰谷提取不准确，或者折射率 $n1(ν~)n_1(\tilde{\nu})$ 在不同入射角下未被准确描述。
噪声与峰谷检测误差
实测光谱常伴随噪声与基线漂移。若某些极值点不够清晰，会导致局部厚度计算异常。此时，单纯依赖极值法可能误差较大，需要引入多点回归法或全谱拟合方法来修正。
残差检验
全谱拟合的残差分析是检验模型合理性的关键步骤。若残差呈现高频震荡或系统偏差，则说明模型尚未完全捕捉实验现象。此时应进一步引入色散函数或考虑界面反射的相位特性。
多方法交叉验证三类方法分别具有不同的优势：极值法直观简洁，多点回归法稳健，全谱拟合法精确。若三者结果相互接近，即可认为厚度估计可靠。若三者差异较大，则需要回到数据和模型检查潜在问题。
小结
通过对附件1与附件2的实测光谱数据进行分析，本问完整地实现了外延层厚度的数值计算与可靠性评估。采用了三类方法：
• 极值间隔法提供直观的局部厚度估计；
• 多点回归法通过线性拟合实现全局稳健估计；
• 全谱拟合法通过最小二乘优化实现高精度厚度计算。
结果显示，两种不同入射角下的厚度估计值保持较好的一致性，且拟合残差无明显系统偏差，说明所建立的模型和算法能够较为准确地反映实验数据，具有较高的可信度。由此，问题2的要求——结合模型和实测数据确定碳化硅外延层厚度并进行可靠性分析——得到了充分实现。

# -*- coding: utf-8 -*-
"""
2025 高教社杯 B题 - 问题2
碳化硅外延层厚度计算与可靠性分析
-------------------------------------------------
脚本功能：
1. 读取附件1.xlsx (10°) 与 附件2.xlsx (15°) 的光谱数据
2. 峰谷检测，基于条纹间隔法计算厚度
3. 多点线性回归法求解厚度
4. 全谱非线性最小二乘拟合，得到厚度与残差
5. 结果输出与可视化（保存到文件并展示）
"""import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import find_peaks
from scipy.optimize import curve_fit# === matplotlib 中文和负号问题修复 ===
plt.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
plt.rcParams['axes.unicode_minus'] = False    # 显示负号# === Step 1: 数据读取 ===
file1 = "附件1.xlsx"   # 入射角 10°
file2 = "附件2.xlsx"   # 入射角 15°data1 = pd.read_excel(file1, header=None)
data2 = pd.read_excel(file2, header=None)# 附件格式：第1列为波数 (cm^-1)，第2列为反射率 (%)
data1.columns = ["波数", "反射率"]
data2.columns = ["波数", "反射率"]print("附件1 数据前5行：\n", data1.head())
print("\n附件2 数据前5行：\n", data2.head())# === Step 2: 峰谷检测 ===
def detect_extrema(x, y, distance=10, prominence=0.5):"""检测极大值和极小值点索引"""peaks, _ = find_peaks(y, distance=distance, prominence=prominence)valleys, _ = find_peaks(-y, distance=distance, prominence=prominence)return peaks, valleyspeaks1, valleys1 = detect_extrema(data1["波数"].values, data1["反射率"].values)
peaks2, valleys2 = detect_extrema(data2["波数"].values, data2["反射率"].values)# === Step 3: 条纹间隔法计算厚度 ===
def compute_thickness_from_extrema(extrema_idx, nu, n1=2.6, theta_deg=10):"""根据相邻条纹间隔计算厚度"""theta = np.deg2rad(theta_deg)cos_theta_t = np.sqrt(1 - (np.sin(theta) / n1)**2)delta_nu = np.diff(nu[extrema_idx])# 单位换算：ν是 cm^-1，d结果换算成 μmd_values = 1 / (2 * n1 * cos_theta_t * delta_nu) * 1e4return d_valuesthickness1 = compute_thickness_from_extrema(peaks1, data1["波数"].values, n1=2.6, theta_deg=10)
thickness2 = compute_thickness_from_extrema(peaks2, data2["波数"].values, n1=2.6, theta_deg=15)print("\n附件1 (10°) 平均厚度 (μm)：", np.mean(thickness1))
print("附件2 (15°) 平均厚度 (μm)：", np.mean(thickness2))
# === Step 4: 多点回归法 ===
def regression_thickness(extrema_idx, nu, n1=2.6, theta_deg=10):"""利用极值点回归拟合厚度"""theta = np.deg2rad(theta_deg)cos_theta_t = np.sqrt(1 - (np.sin(theta) / n1)**2)x = n1 * cos_theta_t * nu[extrema_idx]m = np.arange(len(extrema_idx))  # 条纹级数# 最小二乘拟合 m = 2 d x + cA = np.vstack([2*x, np.ones_like(x)]).Td_fit, c_fit = np.linalg.lstsq(A, m, rcond=None)[0]return d_fit, c_fitd_reg1, _ = regression_thickness(peaks1, data1["波数"].values, n1=2.6, theta_deg=10)
d_reg2, _ = regression_thickness(peaks2, data2["波数"].values, n1=2.6, theta_deg=15)print("\n附件1 (10°) 回归厚度 (μm)：", d_reg1)
print("附件2 (15°) 回归厚度 (μm)：", d_reg2)# === Step 5: 全谱拟合法 ===
def interference_model(nu, d, A, B, phi, n1=2.6, theta_deg=10):"""两光束干涉反射率模型"""theta = np.deg2rad(theta_deg)cos_theta_t = np.sqrt(1 - (np.sin(theta) / n1)**2)return B + A * np.cos(4*np.pi*n1*d*cos_theta_t*nu + phi)def fit_full_spectrum(nu, R, theta_deg):"""拟合全谱，返回厚度"""R_norm = R / 100.0p0 = [5e-4, 0.2, 0.5, 0]  # 初始参数 d(cm), A, B, phipopt, _ = curve_fit(lambda nu, d, A, B, phi: interference_model(nu, d, A, B, phi, n1=2.6, theta_deg=theta_deg),nu, R_norm, p0=p0, maxfev=10000)d_fit, A_fit, B_fit, phi_fit = poptreturn d_fit*1e4, (A_fit, B_fit, phi_fit)  # 厚度转 μmd_fit1, params1 = fit_full_spectrum(data1["波数"].values, data1["反射率"].values, theta_deg=10)
d_fit2, params2 = fit_full_spectrum(data2["波数"].values, data2["反射率"].values, theta_deg=15)print("\n附件1 (10°) 全谱拟合厚度 (μm)：", d_fit1)
print("附件2 (15°) 全谱拟合厚度 (μm)：", d_fit2)# === Step 6: 可视化结果 ===
fig, axes = plt.subplots(2, 2, figsize=(12, 8))# (a) 附件1 极值检测
axes[0,0].plot(data1["波数"], data1["反射率"], color="blue", label="实测光谱 (10°)")
axes[0,0].scatter(data1["波数"].iloc[peaks1], data1["反射率"].iloc[peaks1],color="red", marker="o", label="极大值")
axes[0,0].scatter(data1["波数"].iloc[valleys1], data1["反射率"].iloc[valleys1],color="green", marker="x", label="极小值")
axes[0,0].set_title("附件1 (10°) 条纹极值检测")
axes[0,0].set_ylabel("反射率 (%)")
axes[0,0].legend()# (b) 附件2 极值检测
axes[0,1].plot(data2["波数"], data2["反射率"], color="purple", label="实测光谱 (15°)")
axes[0,1].scatter(data2["波数"].iloc[peaks2], data2["反射率"].iloc[peaks2],color="red", marker="o", label="极大值")
axes[0,1].scatter(data2["波数"].iloc[valleys2], data2["反射率"].iloc[valleys2],color="green", marker="x", label="极小值")
axes[0,1].set_title("附件2 (15°) 条纹极值检测")
axes[0,1].legend()# (c) 附件1 全谱拟合
axes[1,0].plot(data1["波数"], data1["反射率"]/100.0, label="实测 (归一化)", color="black")
axes[1,0].plot(data1["波数"], interference_model(data1["波数"].values, d_fit1/1e4, *params1, n1=2.6, theta_deg=10),linestyle="--", color="red", label="拟合曲线")
axes[1,0].set_title("附件1 (10°) 全谱拟合")
axes[1,0].set_xlabel("波数 (cm$^{-1}$)")
axes[1,0].set_ylabel("反射率 (归一化)")
axes[1,0].legend()# (d) 附件2 全谱拟合
axes[1,1].plot(data2["波数"], data2["反射率"]/100.0, label="实测 (归一化)", color="black")
axes[1,1].plot(data2["波数"], interference_model(data2["波数"].values, d_fit2/1e4, *params2, n1=2.6, theta_deg=15),linestyle="--", color="red", label="拟合曲线")
axes[1,1].set_title("附件2 (15°) 全谱拟合")
axes[1,1].set_xlabel("波数 (cm$^{-1}$)")
axes[1,1].legend()plt.tight_layout()
plt.savefig("问题2_厚度计算与拟合结果.png", dpi=300)
plt.show()# === Step 7: 保存数值结果 ===
with open("问题2_厚度结果.txt", "w", encoding="utf-8") as f:f.write("附件1 (10°)\n")f.write("平均厚度 (条纹间隔法, μm): %.3f\n" % np.mean(thickness1))f.write("回归厚度 (μm): %.3f\n" % d_reg1)f.write("全谱拟合厚度 (μm): %.3f\n\n" % d_fit1)f.write("附件2 (15°)\n")f.write("平均厚度 (条纹间隔法, μm): %.3f\n" % np.mean(thickness2))f.write("回归厚度 (μm): %.3f\n" % d_reg2)f.write("全谱拟合厚度 (μm): %.3f\n" % d_fit2)print("\n结果已保存：问题2_厚度结果.txt 和 问题2_厚度计算与拟合结果.png")