1-理论知识
介绍
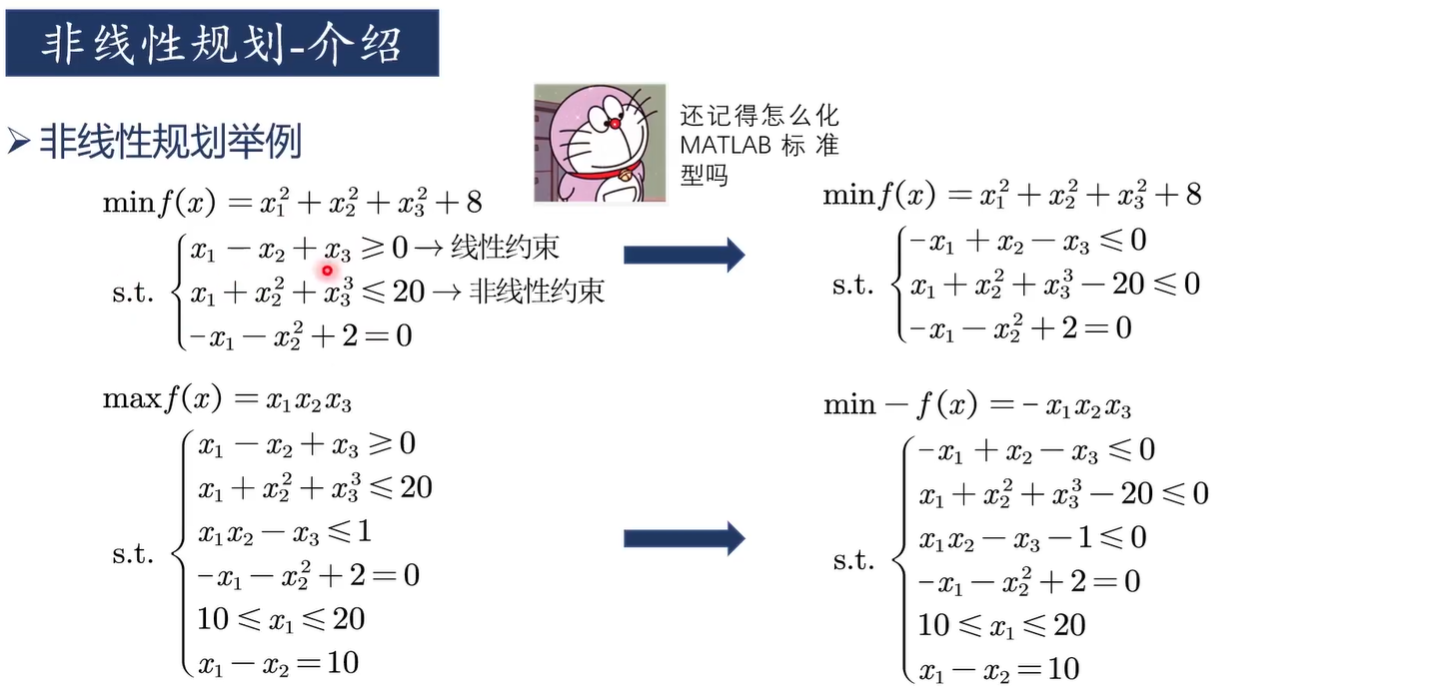
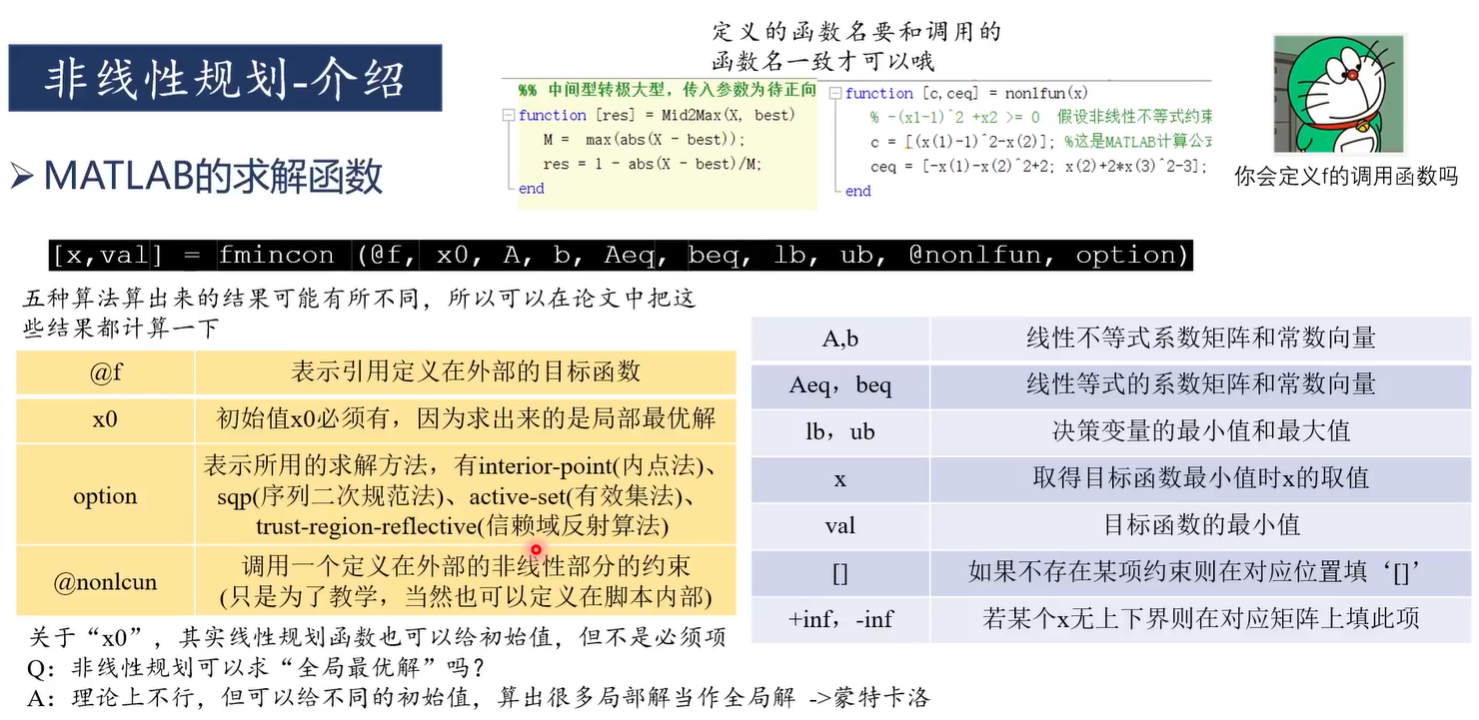

应用







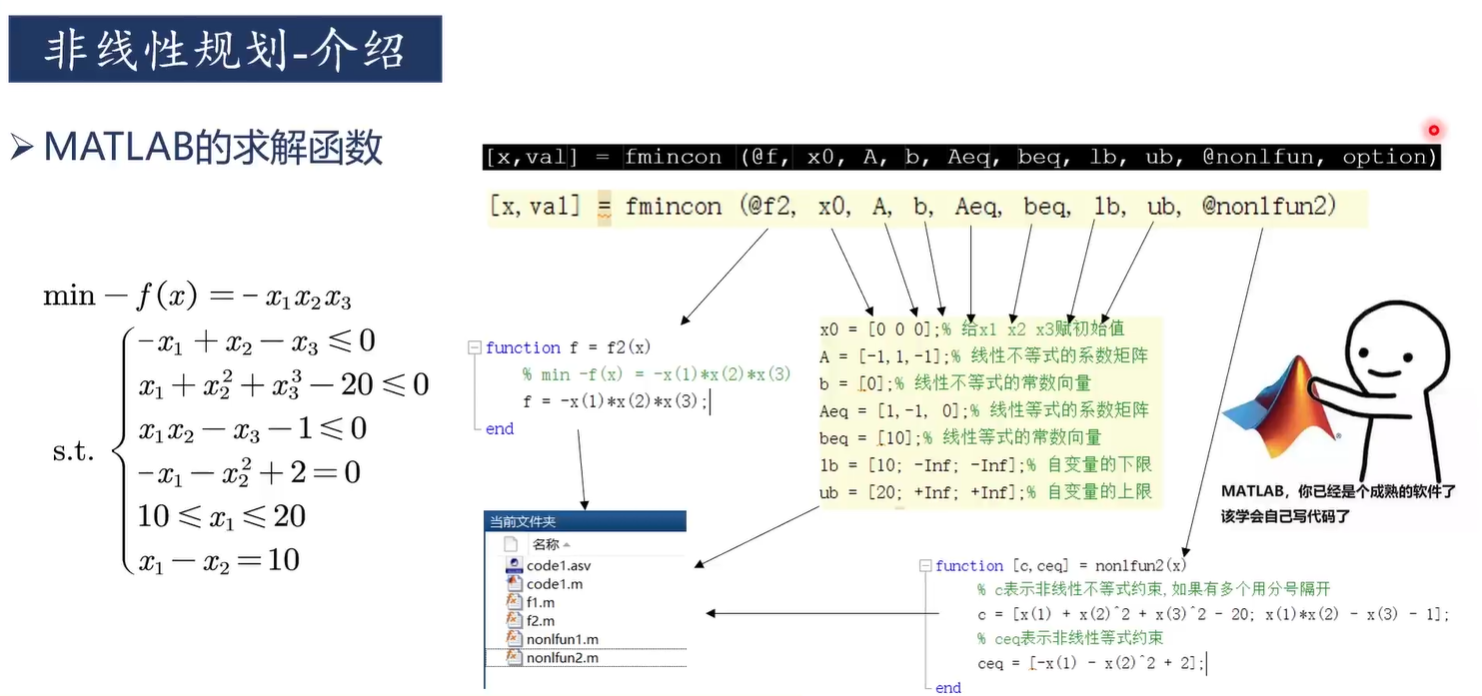
2-基于matlab实现非线性规划
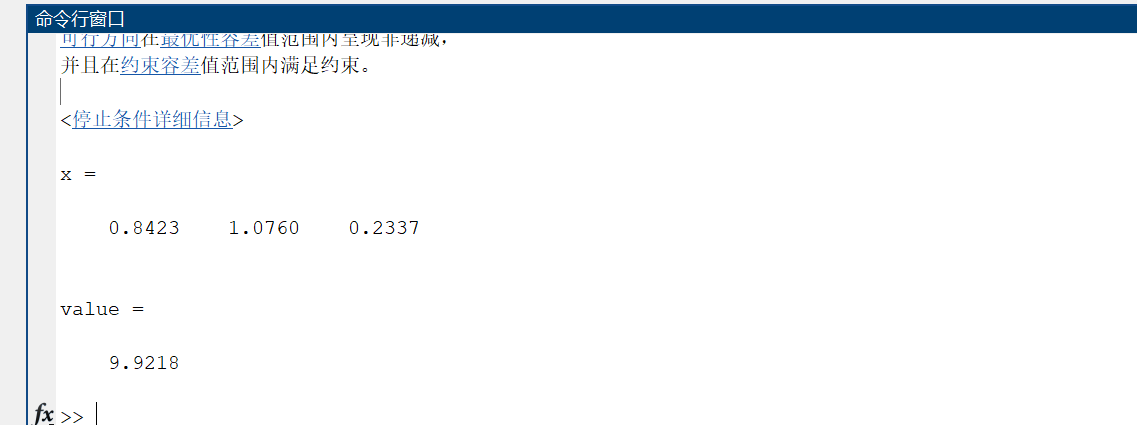
1)例1
% 清除工作台和命令行
clear;clc;
x0=[0 0 0];
A = [-1 1 -1];
b = 0;
[x,value] = fmincon(@f1,x0,A,b,[],[],[],[],@nonlfun1)
function f = f1(x)f = x(1)^2+x(2)^2+x(3)^2+8;
end
function [c,ceq] = nonlfun1(x)c = [x(1)+x(2)^2+x(3)^2-20];ceq = [-x(1)-x(2)^2+2];
end
2)例2

% 清除工作台和命令行
clear;clc;
x0=[0 0 0];
A = [-1 1 -1];
b = 0;
Aeq = [1 -1 0];
beq = 10;
lb = [10;-Inf;-Inf];
ub = [20;+Inf;+Inf];
[x,value] = fmincon(@f1,x0,A,b,Aeq,beq,lb,ub,@nonlfun1);
disp(['x = ' num2str(x)]);
disp(['value = ' num2str(-value)]);
function f = f1(x)f = -x(1)*x(2)*x(3);
end
function [c,ceq] = nonlfun1(x)c = [x(1)+x(2)^2+x(3)^2-20;x(1)*x(2)-x(3)-1];ceq = [-x(1)-x(2)^2+2];
end

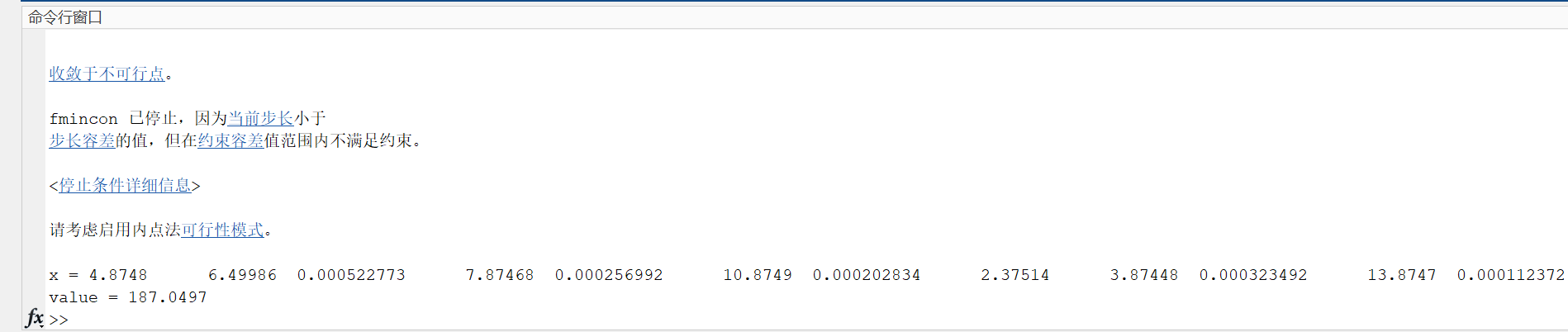
3)怪兽入侵星球问题


%% 清除工作台和命令行
clear;clc;
% 前6个变量为燕双鹰,后6个变量为手撕侠
x0=zeros(1,12);%% 线性不等式约束
% 前6个变量为燕双鹰在6个星球消灭的怪兽量
% 后6个变量为手撕侠在6个星球消灭的怪兽量
A = [ones(1,6),zeros(1,6);zeros(1,6),ones(1,6)];
b = [30;20];
%% 线性等式约束
% 把两个六维单位矩阵作为元素拼在同一行
Aeq = [eye(6),eye(6)];
% 两个人在同一星球消灭的怪兽量之和不超过该星球的怪兽量
beq = [5;9;4;8;14;11];%% 上下界约束
lb = zeros(1,12);
ub = repmat(+Inf,1,12);%% 求解
[x,value] = fmincon(@f1,x0,A,b,Aeq,beq,lb,ub,[]);
value = -value;
disp(['x = ' num2str(x)]);
disp(['value = ' num2str(-value)]);%% 局部函数
function f = f1(x)% 给的是一个行向量% 因计算习惯,把x变成列向量x = x';% 燕双鹰和手撕侠的坐标x1 = 4;y1 = 1;x2 = 8;y2 = 9;% 燕双鹰和手撕侠每消耗一个怪兽需要消耗的馍数p1 = 3;p2 = 1;% 燕双鹰和手撕侠每百公里消耗的馍数k1 = 1;k2 = 3;% 各星球横坐标a = [1.37 9.45 4.43 6.66 3.14 15.92];% 各星球纵坐标b = [10.21 9.45 8.88 5 16.44 18];% 表达式系数矩阵X = x ./ (1+x);% 目标函数,分三行写以提高可读性% % 两人打怪兽消耗的馍数之和f = [repmat(p1,1,6),repmat(p2,1,6)]*x;% i=1,x1j/(1 + x1j) = X([1:6],:)f = f + sqrt(sum(([a;b] - repmat([x1;y1],1,6)) .^ 2)) .* repmat(k1,1,6) * X([1:6],:);% i=2,x2j/(1 + x2j) = X([7:12],:)f = f + sqrt(sum(([a;b] - repmat([x2;y2],1,6)) .^ 2)) .* repmat(k2,1,6) * X([7:12],:);
end
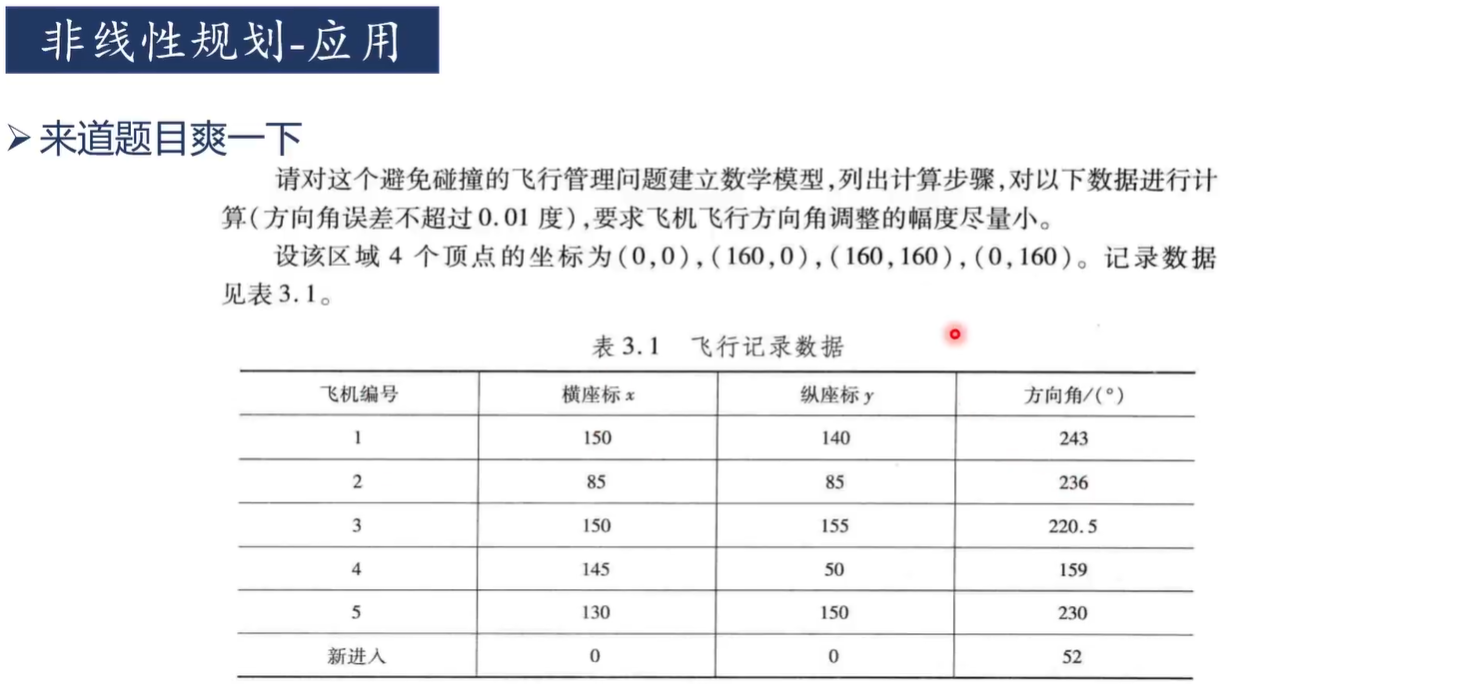
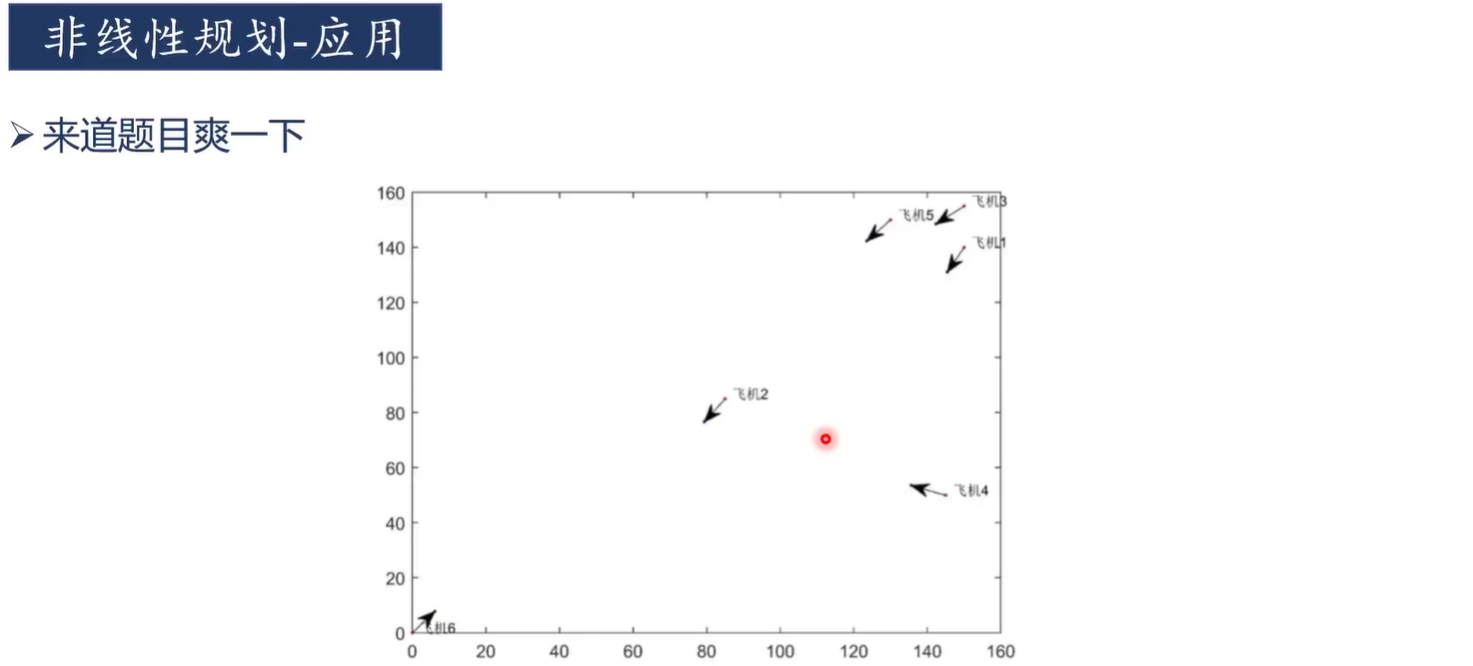
4)飞机碰撞问题




















