波浪模型SWAN学习（2）——波浪浅化模拟（Shoaling on sloping beach）

由于工作原因，最近开始接触波浪模型，所以学习一下SWAN，顺便做个记录、

SWAN是由Delft大学开发的第三代波浪模型，它基于动谱平衡方程，考虑了波-波的非线性作用，对近海、
与模型原理相关的内容详见以下论文：

1. Booij, N., R.C. Ris and L.H. Holthuijsen, 1999, A third-generation wave model for coastal regions, Part I, Model description and validation, J. Geophys. Res. C4, 104, 7649-7666.¹
2. Ris, R.C., N. Booij and L.H. Holthuijsen, 1999, A third-generation wave model for coastal regions, Part II, Verification, J. Geophys. Res. C4, 104, 7667-7681.²

目前，SWAN模型支持结构化矩形网格、曲边矩形网格、非结构化三角形网格。本人暂时从简单的结构化矩形网格开始学习。

希望大家能留言，来相互交流！

SWAN主页：https://swanmodel.sourceforge.io/
用户手册：https://swanmodel.sourceforge.io/online_doc/swanuse/swanuse.html
原理手册：https://swanmodel.sourceforge.io/

算例简介

该算例模拟了波浪在一个斜坡上的传播过程，包含一个线性斜坡（水深从0~20m）和一个阶梯状斜坡（包含两个台阶，第一级水深为1 m，第二级水深为200 m），计算域为一长方形（长16 km，宽4 km）。在模拟过程中，波浪将从下方边界（South）进入。该模拟问题中包含四个算例，如下表所示：

算例编号	斜坡形式	计算网格种类
1	线性	结构化矩形网格
2	线性	非结构化三角形网格
3	阶梯式	结构化矩形网格
4	阶梯式	非结构化三角形网格

两种水深配置如下图所示：

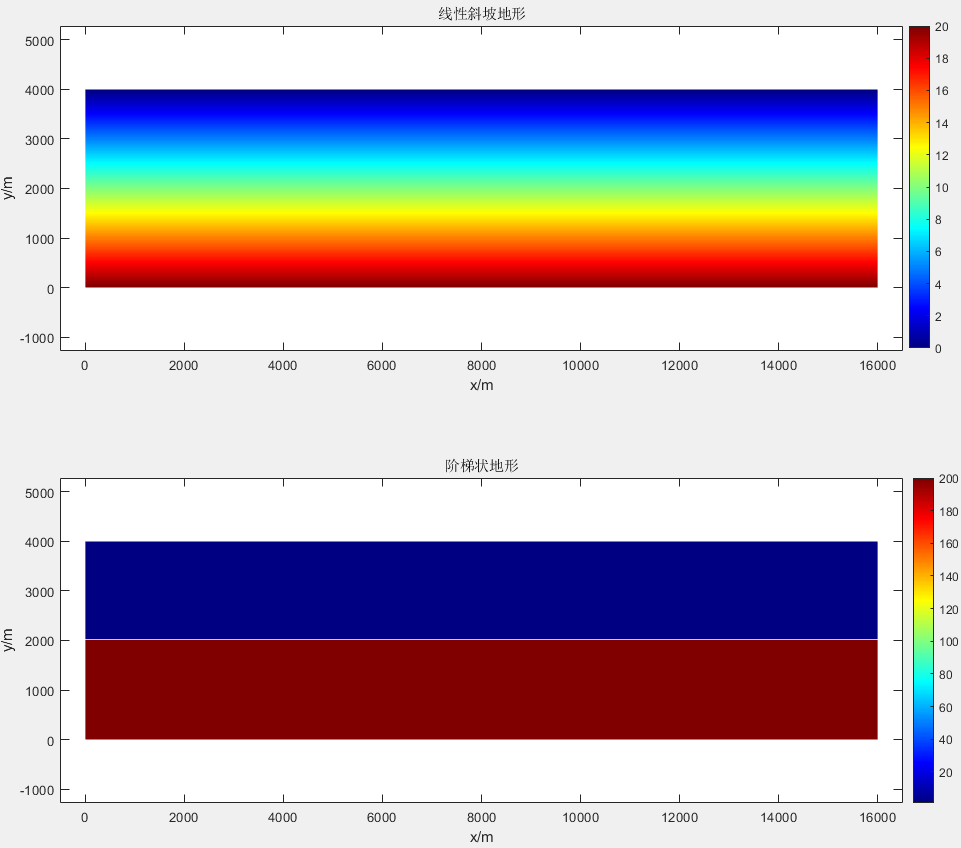
两种计算网格配置如下图所示：

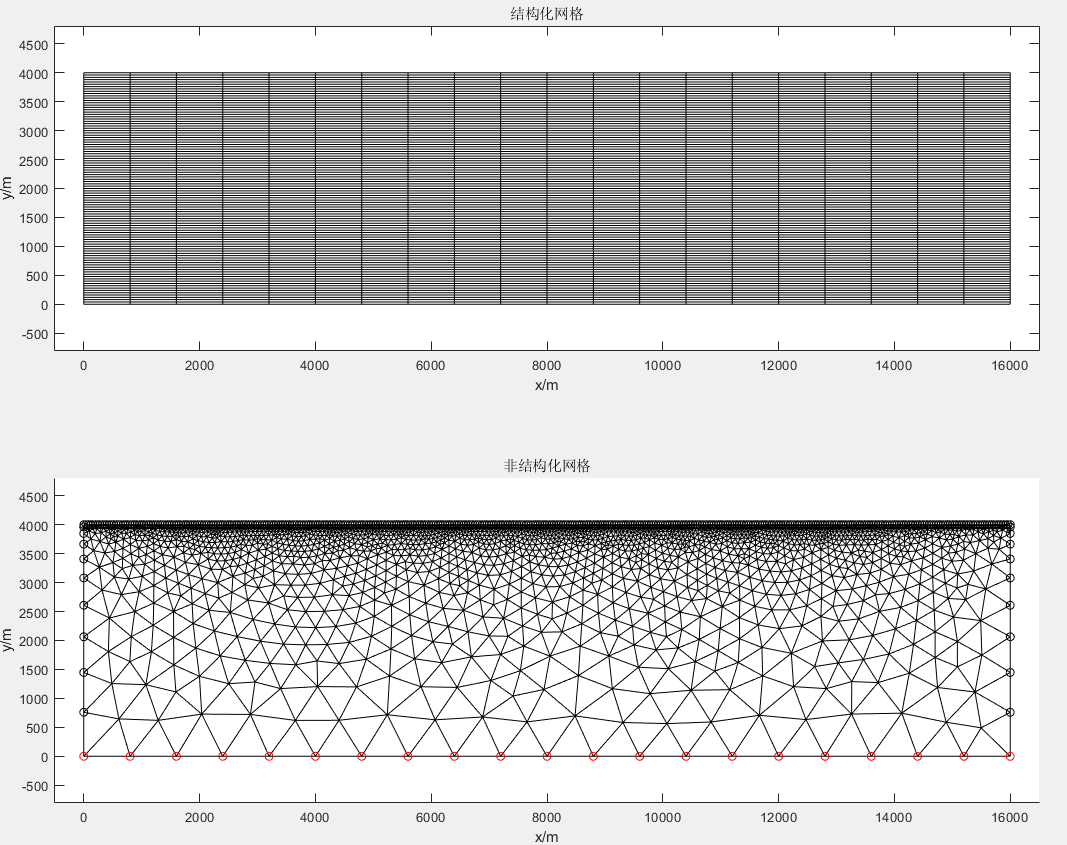
（注：在三角形网格中，红色圆点表示编号为1的边界，黑色圆点表示编号为2的边界）

该算例的输入文件可在SWAN官网下载，下载连接是https://swanmodel.sourceforge.io/download/zip/shoal.tar.gz。

输入文件

本模拟问题的输入文件如下：

a21sho01.swn            : SWAN input file with rectangular grid and sloping beach (算例1)
a21sho02.swn            : SWAN input file with unstructured grid and sloping beach (算例2)
a21sho03.swn            : SWAN input file with rectangular grid and stepwise beach profile (算例3)
a21sho04.swn            : SWAN input file with unstructured grid and stepwise beach profile (算例4)
a21shoa.bot             : contains bottom values of sloping beach (线性斜坡)
step.bot                : contains bottom values of stepwise beach profile (阶梯状斜坡)
a21shoa.loc             : contains some locations in problem area (用于指定输出点的位置)
a21shoa.node            : contains coordinates of nodes in unstructured mesh (三角形网格的节点)
a21shoa.ele             : contains elements in unstructured mesh (构成三角形网格的节点编号)
a21shoa.ana             : contains analytical solution for sloping beach case (解析解数据)

由于本算例的边界设置及参数设置较为简单，以下仅作简要介绍。在此之前，先介绍本模拟问题中三角形网格的输入方式。

三角形网格

在本模拟问题中，三角形网格的数据格式类似Triangle库中的数据格式（关于Triangle库详见《学习使用Triangle库》）。描述三角形网格的文件包括两个，第一个是存储三角形顶点坐标的.node文件，其格式如下：

## 第一行： <节点总数> <图形维数(该值一般为2)> <是否有结点属性值(0 or 1)> <是否有边界点标记(0 or 1)>
## 另起一行，按下列格式输入数据：<节点编号(一般以1,2,3...顺序依次输入)> <节点x坐标> <节点y坐标> [节点属性值]  [节点边界标记]

本算例中的a21shoa.node中的数据如下：

        2612           2           0           11   608.0209       646.0940               02  0.0000000E+00  0.0000000E+00           13   800.0000      0.0000000E+00           14  0.0000000E+00   760.0000               2...

它表示网格中一共有2612个节点，数据文件中不含属性值，但有边界标记。从第二行开始，每行的四个数依次表示节点编号、节点x坐标、节点y坐标、节点的边界标记（0表示节点在计算区内部，1、2分别表示节点在第1号、第2号边界上）。

第二个数据文件是a21shoa.ele，其数据格式如下：

##第一行： <三角网格总数> <三角形各顶点的节点编号(由三个数字构成)> <网格中心是否有属性值(0 or 1)> ##余下各行：<网格编号> <节点1> <节点2>  <节点3> ... [网格中心点的属性值] 

在本算例中，数据内容如下：

        4782           3           01           1           2           32           1           4           23           1           3           54           1           6           45           7           1           56           7           6           17           3           8           58           9           4           6

它表示网格中共有4782个三角形；从第二行开始，每行的第一个数字表示网格编号，第2、3、4个数字分别表示构成该网格的三个点的node编号。

参数文件 (.swn)

算例1

首先，介绍算例1的参数设置。模型计算域的长和宽分别为16000 m和4000 m，在这两个方向上分别均分20个和100个网格；模型计算了80 ~ 130°方向上的波浪，并将该方向均分了mdc = 80个小份进行离散；模型考虑了频率范围在 0.05 ~ 0.25 Hz的波浪，msc = 40 表示频域上离散的网格数。此外，模型在指定边界条件时候指定了高斯谱（GAUSS），并给出其中的参数${\sigma }_{fr}=0.01$，指定谱峰周期为波浪的特征周期，入射波在波向上的摆动采用POWER形式。上述内容对应的指令参数如下：

CGRID 0. 0. 0. 16000. 4000. 20 100 SECTOR 80. 100. 80 0.05 0.25 40
$
INPGRID BOTTOM 0. 0. 0. 1 1 16000. 4000.
READINP BOTTOM 1. 'a21shoa.bot'  1 0 FREE
$
BOUN SHAPE GAUSS 0.01 PEAK DSPR POWER
BOUN SIDE S CCW CON PAR 1. 10. 90. 500.

模型不考虑波浪折射（REFRAC）、四波相互作用（QUAD）、不考虑水深变化所致波浪破碎（BREA）、 不考虑白浪耗散（WCAP）。

OFF REFRAC
OFF QUAD
OFF BREA
OFF WCAP

模型的输出包含两个部分，第一是线段(8000,0) - (8000, 4000)上的波浪数据（.tab文件），第二是a21shoa.loc中各个点的波浪数据（.spc文件）。

CURVE  'LINE1' 8000. 0.  100  8000. 4000.
TABLE  'LINE1' HEAD                  DIST DEP HS RTP TM01 TM02 DSPR DIR TRANSP
TABLE  'LINE1' HEAD   'a21sho01.tab' DIST DEP HS RTP TM01 TM02 DSPR DIR TRANSP
$
POINTS 'POINT' FILE   'a21shoa.loc'
SPEC   'POINT' SPEC1D 'a21sho01.spc'
TABLE  'POINT' HEAD   'a21sho01.tbl' HS RTP TM01 TM02 FSPR TRANSP

其它算例

相较于算例1，算例2更换了网格设置而其他设置均不变。读入非结构化网格的指令如下：

CGRID UNSTRUCTURED SECTOR 80. 100. 80 0.05 0.25 40
READ UNSTRUCTURED TRIANGLE 'a21shoa'

相较于算例1，算例3改变了水深配置而其他设置均不变。读入阶梯状水深数据（step.bot）的指令如下：

INPGRID BOTTOM 0. 0. 0. 1 100 16000. 40.
READINP BOTTOM 1. 'step.bot'  1 0 FREE

而对于算例4，它采用了非结构化网格和阶梯状水深配置，其指令与本节上述两个算例类似。

模型的运行与结果

将输入文件复制到swan.exe同一文件夹下（如何编译得到swan.exe详见《波浪模型SWAN学习（1）——模型编译与波浪折射模拟（Test of the refraction formulation）》），之后在终端中输入如下指令进行运行（以并行模式为例）：

./swanrun -input [inputfile] -mpi [n]

其中的[inputfile]表示.swn文件的文件名（不带扩展名），[n]表示并行线程数。需要注意的是，对于非结构化网格，目前的代码不支持并行计算，因此在运行非结构化网格算例时，一定要将并行线程数设置为1。

以下对比了算例1和2中模拟所得特征波高（H_s）、平均波向（Dir）结果与对应的解析解结果，如下图所示。图中的红色圆圈表示模拟值，黑线表示解析值。解析解数据在输入文件压缩包中。

---

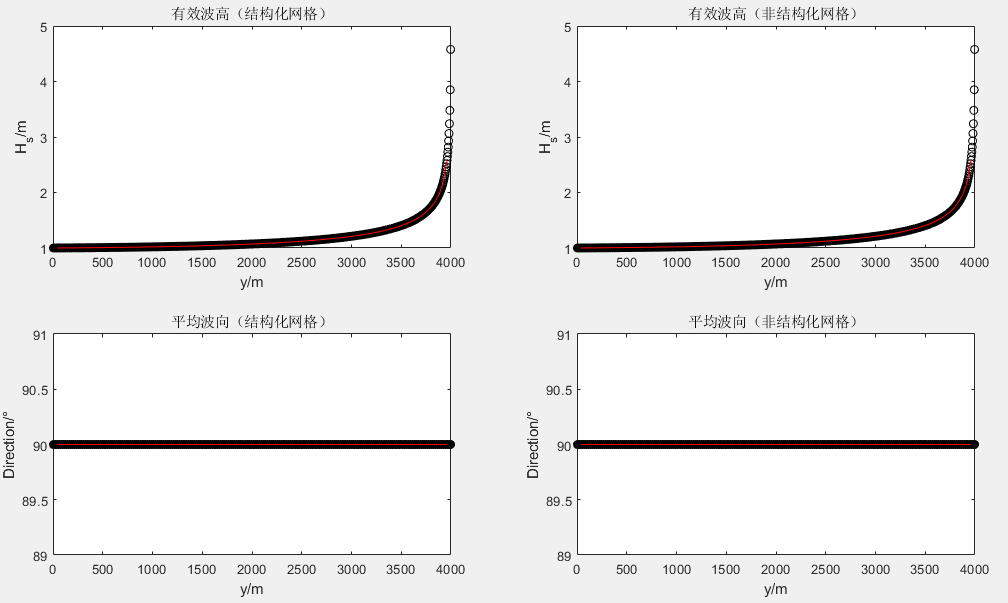
1. https://doi.org/10.1029/98JC02622 ↩︎

2. https://doi.org/10.1029/1998JC900123 ↩︎