2.插值法
插值法
对于某个区间连续函数,我们只知道一些点的函数值,或者函数有表达式但是计算过于复杂。用于求解其他点或者求解表达式,通过拟合近似代替原函数的方法,通常使用插值法。
内插
内插是指在已知数据点所构成的区间内部,估计未知点的值。相对可靠和准确。因为未知点被已知点所包围,插值函数或模型在这个区间内有数据支撑,结果通常更可信。
外插
外插是指在已知数据点所构成的区间外部,估计未知点的值。它通常被称为预测。非常不可靠且风险高。因为没有任何已知数据来约束模型在区间外的行为,模型可能会做出完全错误的预测。外插的距离越远,不确定性就越大,结果通常极不可信。
满足差值条件的不超过n次的插值多项式是存在且唯一的。(插值n次)
拉格朗日差值
对于一组给定的点,拉格朗日插值法总能给出一个函数穿过这些点。
面面俱到是优点,但也是缺点,因为如果有离群点会严重影响拟合效果,这也意味着预处理对噪音的去除很重要
线性插值
一次插值多项式:需要两个点
抛物差值
二次插值多项式:需要三个点
求解基函数
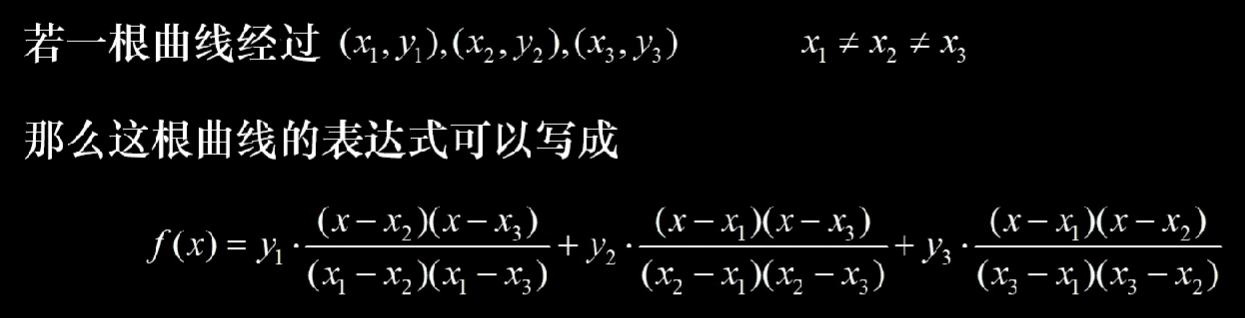
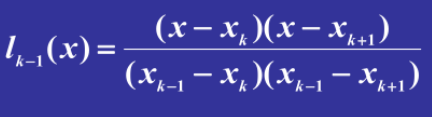
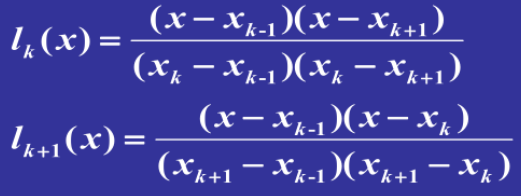
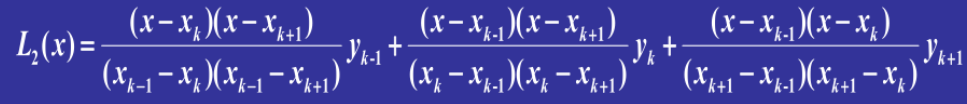
多次插值
对于n+1个点的插值,需要插值n次,即n次多项式
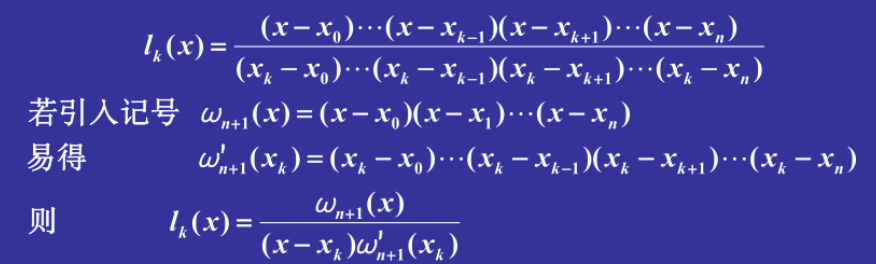
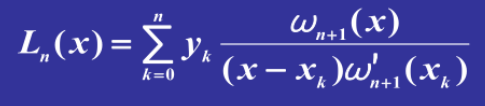
插值余项与误差估计


