从数据生成到不确定性估计：用 LSTM + 贝叶斯优化实现时间序列多步预测

在时间序列预测领域，如何构建精准且能量化不确定性的模型一直是核心挑战。本文将拆解一份完整的时间序列预测代码，从虚拟数据生成、滑窗数据集构建，到 LSTM 模型训练、贝叶斯优化超参数，再到 MC Dropout 不确定性估计，带你完整掌握工业级时间序列预测的实现逻辑。

一、代码核心框架：从数据到可视化的全流程

这份代码并非单一功能的脚本，而是一套端到端的时间序列预测解决方案。其核心流程可分为 8 个关键模块，每个模块环环相扣，共同构成完整的预测体系：

虚拟时间序列生成（模拟真实业务数据特征）
滑窗数据集构建与标准化（避免数据泄露的关键）
PyTorch 数据集与 LSTM 模型定义（预测模型核心）
模型训练与评估函数封装（高效迭代训练）
贝叶斯优化超参数搜索（自动寻找最优参数）
融合训练集与验证集重训最终模型（最大化数据价值）
MC Dropout 不确定性估计（量化预测置信度）
多维度可视化分析（结果解读与模型验证）

接下来，我们将逐一拆解每个模块的核心逻辑与设计思路。

二、模块拆解：关键技术与代码解析

1. 虚拟时间序列生成：模拟真实数据的 “五维特征”

真实世界的时间序列往往包含趋势、周期性、突发波动和噪声，代码通过五重特征叠加生成贴近业务场景的数据，避免用纯随机数据导致的 “模型过拟合假象”：

# 趋势项：模拟长期增长/下降（如用户增长、销售额上升）
trend = 0.0015 * t
# 双周期项：模拟不同频率的周期性波动（如日周期、周周期）
season1 = 1.2 * np.sin(2 * np.pi * t / 200)  # 长周期
season2 = 0.6 * np.sin(2 * np.pi * t / 30 + 0.7)  # 短周期
# 突发尖峰：模拟异常值（如促销日销量突增、设备故障突发波动）
spikes = np.zeros_like(t, dtype=float)
for _ in range(18):pos = np.random.randint(50, T-50)spikes += np.exp(-0.5*((t-pos)/5)**2) * (np.random.rand()*3 + 1)
# 噪声项：模拟测量误差或随机扰动
noise = 0.4 * np.random.randn(T)
# 最终序列：基础值+趋势+周期+尖峰+噪声
y = 5.0 + trend + season1 + season2 + spikes + noise

这种数据生成方式的优势在于：可复现、特征明确，能精准测试模型对不同时间序列成分的拟合能力，尤其适合算法验证阶段。

2. 滑窗数据集：避免数据泄露的 “黄金法则”

时间序列预测中，“用未来数据预测过去” 是常见的低级错误，代码通过滑窗法构建数据集，从根源上杜绝数据泄露：

def make_windows(series, p, H):X, Y = [], []# p：历史窗口长度（用过去p个点预测未来）# H：预测窗口长度（一次预测未来H个点）for i in range(len(series) - p - H + 1):X.append(series[i:i+p])  # 输入：过去p个点（历史数据）Y.append(series[i+p:i+p+H])  # 输出：未来H个点（待预测值）return np.array(X), np.array(Y)

同时，代码在数据划分和标准化环节进一步强化 “无泄露” 原则：

数据集划分：按 7:1.5:1.5 分为训练集、验证集、测试集，严格遵循时间顺序（不随机打乱）
标准化：仅用训练集的均值和标准差对所有数据（训练 / 验证 / 测试）进行标准化，避免验证集 / 测试集的统计信息影响模型训练

3. LSTM 模型：为何选择 “直接多输出” 而非 “递归预测”？

代码实现的LSTMDirect模型采用直接多输出策略（一次预测未来 H 个点），而非传统的 “递归预测”（用前一步预测值作为下一步输入），这一设计背后有重要考量：

运行
class LSTMDirect(nn.Module):def __init__(self, input_size=1, hidden_size=64, num_layers=2, dropout=0.2, H=10):super().__init__()# LSTM层：捕捉时间序列的长期依赖self.lstm = nn.LSTM(input_size, hidden_size, num_layers,batch_first=True, dropout=dropout if num_layers>1 else 0.0)# 全连接层：将LSTM输出映射为H个预测值（直接多输出）self.head = nn.Linear(hidden_size, H)def forward(self, x):x = x.unsqueeze(-1)  # 适配LSTM输入格式：[batch, seq_len, input_size]out, _ = self.lstm(x)  # LSTM输出：[batch, seq_len, hidden_size]h_last = out[:, -1, :]  # 取最后一个时间步的输出（包含整个序列的信息）y = self.head(h_last)  # 输出：[batch, H]（一次预测未来H个点）return y

直接多输出的优势：

避免递归预测的 “误差累积” 问题（递归时前一步的预测误差会传递到后一步）
训练效率更高（一次迭代即可优化 H 个预测目标，无需分步预测）
更适合工业场景中 “批量预测未来多步” 的需求（如预测未来 7 天的销量）

4. 贝叶斯优化：让超参数搜索 “更聪明”

手动调参效率低且依赖经验，代码用贝叶斯优化（BO） 自动寻找最优超参数，核心是 “利用历史搜索结果指导下一步搜索”，而非随机试错：
（1）超参数搜索空间定义
首先明确需要优化的超参数及范围：

space = {'hidden_size': (16, 128),  # LSTM隐藏层维度'num_layers': (1, 3),      # LSTM层数'lr': (1e-4, 5e-2),        # 学习率（对数空间搜索）'dropout': (0.0, 0.5),     #  dropout概率（防止过拟合）'batch_size': (16, 128)    # 批次大小
}

（2）贝叶斯优化核心逻辑
初始随机采样：先随机测试 6 组超参数，建立初始的 “超参数 - 模型性能” 映射
高斯过程（GP）建模：用高斯过程拟合历史数据，预测未知超参数对应的模型性能及不确定性
期望改进（EI）准则：优先选择 “可能带来性能提升” 的超参数（平衡 “探索未知区域” 和 “利用已知最优区域”）
迭代优化：每次迭代后更新高斯过程模型，直到完成 18 次搜索（可根据算力调整）

对比传统网格搜索 / 随机搜索：

效率更高：无需遍历所有可能的超参数组合，通常只需几十次迭代即可找到接近最优的参数
更智能：利用概率模型指导搜索方向，避免在性能差的区域浪费算力

5. MC Dropout：量化预测的 “不确定性”

在金融、能源等核心场景中，仅给出预测值是不够的 —— 还需要知道 “这个预测有多可信”。代码通过MC Dropout实现不确定性估计：

def mc_dropout_preds(model, X_s, mc_runs=80):model.train()  # 关键：训练模式下Dropout才会生效preds = []# 多次前向传播（每次Dropout随机关闭部分神经元）for _ in range(mc_runs):batch_preds = []for xb, _ in loader:xb = xb.to(device)p = model(xb).cpu().numpy()batch_preds.append(p)preds.append(np.vstack(batch_preds))# 计算不确定性：多次预测的均值（最终预测值）和标准差（不确定性度量）preds = np.stack(preds, axis=0)mean = preds.mean(axis=0)  # 预测均值std = preds.std(axis=0)    # 预测标准差（越大，不确定性越高）return mean, std

不确定性估计的价值：

帮助业务决策：若预测某产品未来销量的标准差很大（不确定性高），可采取更保守的库存策略
模型监控：若某段时间预测标准差突然增大，可能是数据分布发生变化（需重新训练模型）

6. 可视化分析：让结果 “看得见、可解释”

代码生成 6 张核心图表，从不同维度解读模型性能，这是工业级代码的重要组成部分（仅展示关键图表的解读逻辑）：

图表类型 核心解读 业务价值
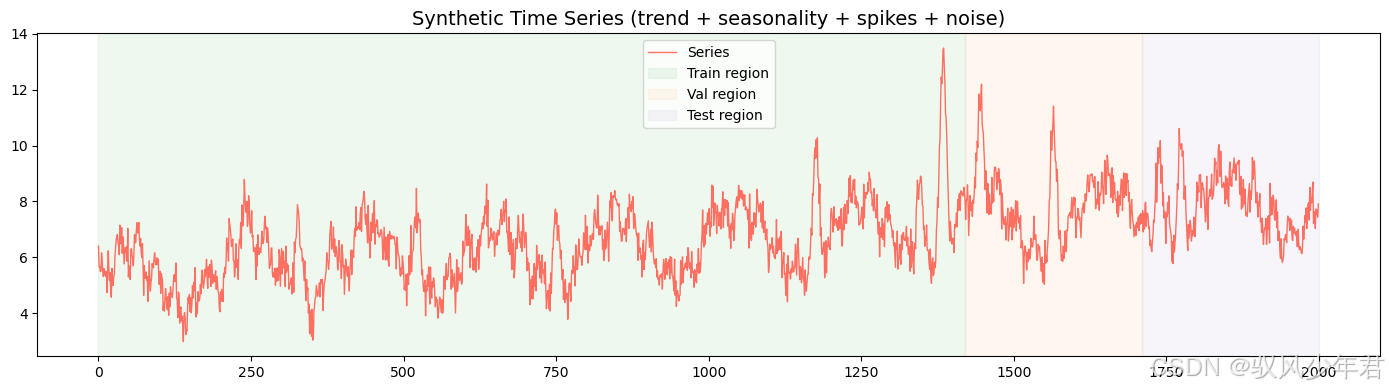
合成序列分布图 展示数据的趋势、周期、尖峰特征，以及训练 / 验证 / 测试集的划分 验证数据生成的合理性，明确模型需要拟合的特征
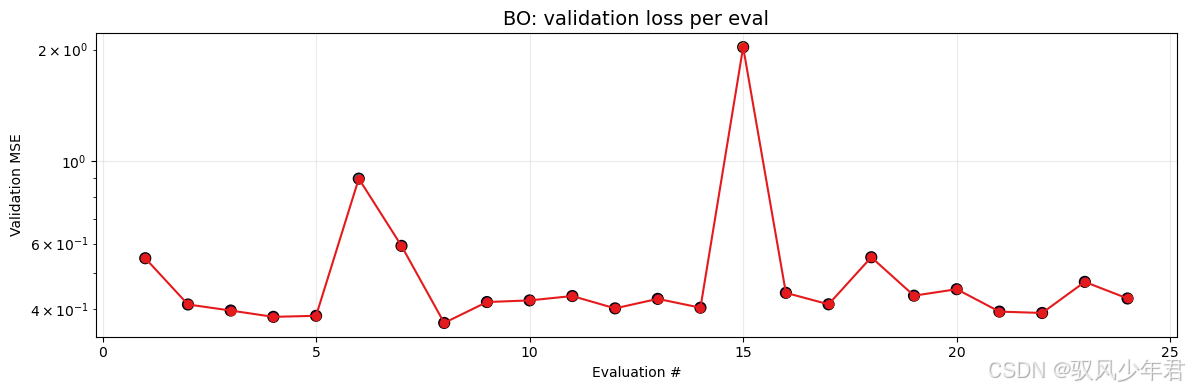
贝叶斯优化损失曲线 展示每次超参数评估的验证损失变化，看是否收敛到最优值 验证贝叶斯优化的有效性，判断是否需要增加迭代次数
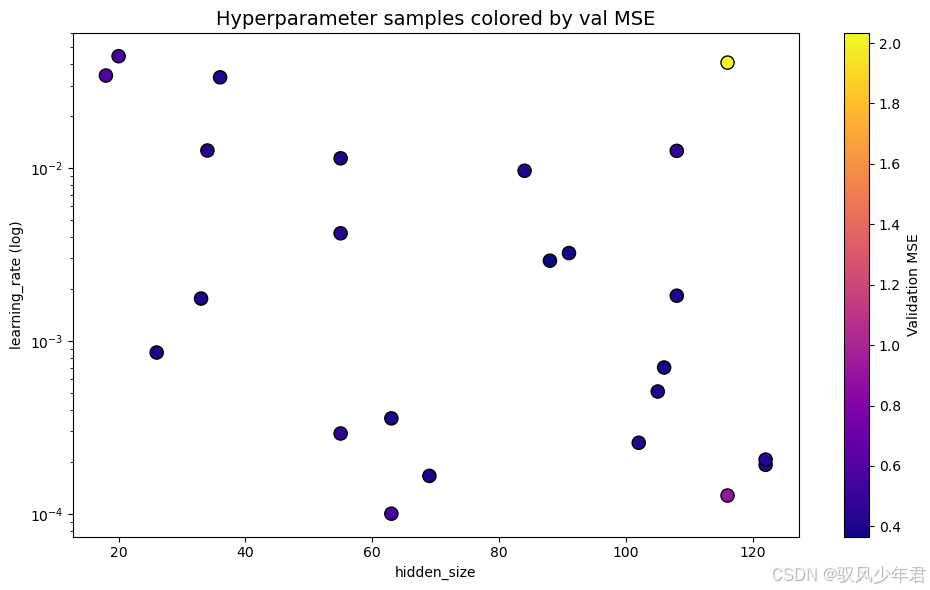
超参数散点图 展示超参数组合与验证损失的关系（如 hidden_size vs 学习率） 发现超参数的敏感性（如学习率过高会导致损失骤增）
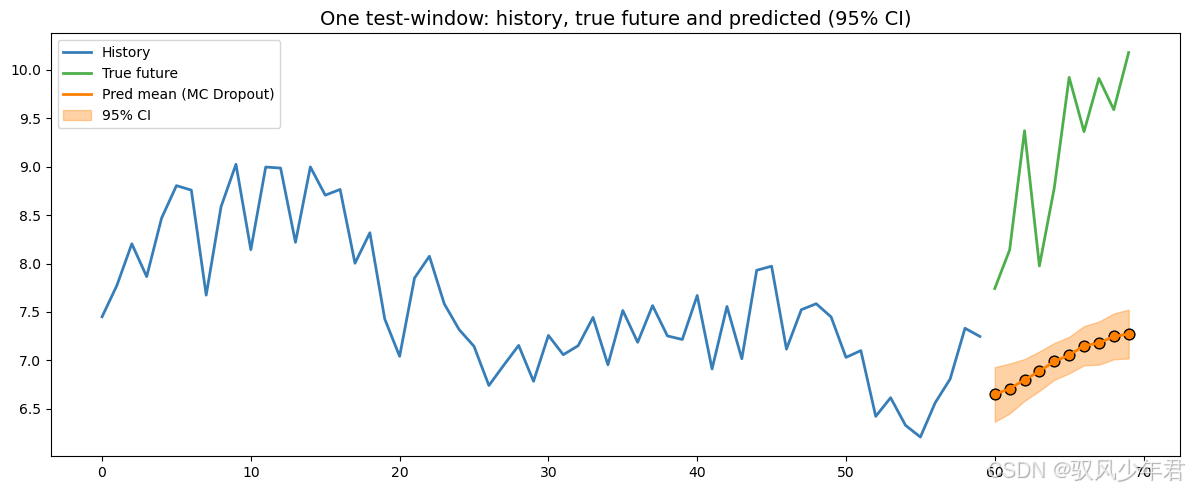
单窗口预测对比图 展示单个测试窗口的历史数据、真实未来值、预测值及 95% 置信区间 直观验证模型的预测精度和不确定性估计的合理性

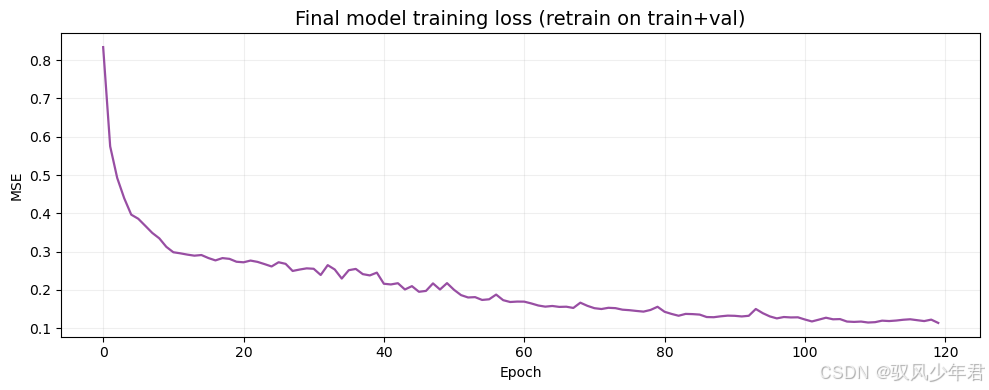
训练损失曲线 展示最终模型的训练损失变化，看是否收敛 验证模型训练的稳定性，判断是否存在过拟合

三、核心亮点与工业级实践启示

这份代码不仅是 “能跑通的 Demo”，更包含诸多工业级实践细节，值得借鉴：

1. 数据泄露防护的 “三重保障”
   滑窗数据集构建：严格按时间顺序划分输入输出，不跨越时间边界
   标准化策略：仅用训练集统计量标准化所有数据
   数据集划分：训练 / 验证 / 测试集严格按时间顺序划分，不随机打乱
2. 模型鲁棒性设计
   Dropout 正则化：防止 LSTM 过拟合（尤其在训练数据有限时）
   梯度裁剪：torch.nn.utils.clip_grad_norm_(model.parameters(), 3.0)，避免训练过程中梯度爆炸
   早停策略：验证损失连续 6 轮不下降则停止训练，防止过拟合
3. 工程化封装
   训练 / 评估函数封装：train_one()、evaluate()、fit_model()，提高代码复用性
   超参数搜索与模型重训分离：先通过验证集优化超参数，再用训练 + 验证集重训最终模型，最大化数据价值

四、进一步优化方向

若要将这份代码应用到实际业务中，可从以下方向优化：

数据层面：替换为真实业务数据（如销量、流量、温度），并增加数据预处理步骤（如异常值修复、缺失值填充）
模型层面：尝试更复杂的模型（如 Transformer-Time Series、N-Beats），或在 LSTM 中加入注意力机制（捕捉关键时间步）
不确定性估计层面：对比其他方法（如贝叶斯神经网络、集成学习），选择更适合业务场景的不确定性度量方式
工程层面：加入模型保存 / 加载逻辑、日志记录、超参数可视化 dashboard，方便线上部署与监控

五、总结

这份代码完整覆盖了时间序列预测的 “数据生成 - 模型构建 - 超参优化 - 结果解读” 全流程，核心是用 LSTM 直接多输出实现精准预测，用贝叶斯优化提高调参效率，用 MC Dropout 量化不确定性。无论是初学者学习时间序列预测的核心逻辑，还是工程师搭建工业级预测系统，都能从中获得启发。

如果需要进一步落地，建议先针对具体业务场景（如销量预测、设备故障预测）调整数据预处理和模型参数，再通过 A/B 测试验证模型在真实业务中的效果。

完整代码

import math, time, random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import MaxNLocator
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import Matern, WhiteKernel, ConstantKernel as C
from sklearn.preprocessing import StandardScaler
from scipy.stats import norm# 1. 生成虚拟时间序列
np.random.seed(42)
T = 2000
t = np.arange(T)
trend = 0.0015 * t
season1 = 1.2 * np.sin(2 * np.pi * t / 200)
season2 = 0.6 * np.sin(2 * np.pi * t / 30 + 0.7)
spikes = np.zeros_like(t, dtype=float)
for _ in range(18):pos = np.random.randint(50, T-50)spikes += np.exp(-0.5*((t-pos)/5)**2) * (np.random.rand()*3 + 1)
noise = 0.4 * np.random.randn(T)
y = 5.0 + trend + season1 + season2 + spikes + noise# 2. 构造滑窗数据集（避免数据泄露）
def make_windows(series, p, H):X, Y = [], []for i in range(len(series) - p - H + 1):X.append(series[i:i+p])Y.append(series[i+p:i+p+H])return np.array(X), np.array(Y)p = 60   # history length
H = 10   # forecast horizon (direct multi-output)
X, Y = make_windows(y, p, H)
n = X.shape[0]train_end = int(n * 0.7)
val_end = int(n * 0.85)
X_train, Y_train = X[:train_end], Y[:train_end]
X_val, Y_val = X[train_end:val_end], Y[train_end:val_end]
X_test, Y_test = X[val_end:], Y[val_end:]# 标准化：仅用训练集统计量（关键防止泄露）
scaler_x = StandardScaler().fit(X_train.reshape(-1,1))
scaler_y = StandardScaler().fit(Y_train.reshape(-1,1))
def scale_xy(X_raw, Y_raw, sx=scaler_x, sy=scaler_y):Xs = sx.transform(X_raw.reshape(-1,1)).reshape(X_raw.shape)Ys = sy.transform(Y_raw.reshape(-1,1)).reshape(Y_raw.shape)return Xs, Ys
X_train_s, Y_train_s = scale_xy(X_train, Y_train)
X_val_s, Y_val_s = scale_xy(X_val, Y_val)
X_test_s, Y_test_s = scale_xy(X_test, Y_test)# 3. PyTorch Dataset & Model
class TimeSeriesDataset(Dataset):def __init__(self, X, Y):self.X = torch.tensor(X, dtype=torch.float32)self.Y = torch.tensor(Y, dtype=torch.float32)def __len__(self):return len(self.X)def __getitem__(self, idx):return self.X[idx], self.Y[idx]class LSTMDirect(nn.Module):def __init__(self, input_size=1, hidden_size=64, num_layers=2, dropout=0.2, H=10):super().__init__()self.hidden_size = hidden_sizeself.num_layers = num_layersself.lstm = nn.LSTM(input_size, hidden_size, num_layers,batch_first=True, dropout=dropout if num_layers>1 else 0.0)self.head = nn.Linear(hidden_size, H)self.dropout = nn.Dropout(dropout)def forward(self, x):x = x.unsqueeze(-1)  # batch x seq_len x 1out, _ = self.lstm(x)h_last = out[:, -1, :]h_last = self.dropout(h_last)y = self.head(h_last)return ydevice = torch.device('cuda' if torch.cuda.is_available() else 'cpu')# 4. 训练 / 评估 函数
def train_one(model, opt, loss_fn, loader):model.train()total_loss = 0.0for xb, yb in loader:xb, yb = xb.to(device), yb.to(device)pred = model(xb).squeeze()loss = loss_fn(pred, yb)opt.zero_grad()loss.backward()torch.nn.utils.clip_grad_norm_(model.parameters(), 3.0)opt.step()total_loss += loss.item() * xb.size(0)return total_loss / len(loader.dataset)def evaluate(model, loss_fn, loader):model.eval()total_loss = 0.0preds, trues = [], []with torch.no_grad():for xb, yb in loader:xb, yb = xb.to(device), yb.to(device)pred = model(xb).squeeze()total_loss += loss_fn(pred, yb).item() * xb.size(0)preds.append(pred.cpu().numpy())trues.append(yb.cpu().numpy())preds = np.vstack(preds) if preds else np.zeros((0,H))trues = np.vstack(trues) if trues else np.zeros((0,H))return total_loss / len(loader.dataset), preds, truesdef fit_model(hparams, epochs=50, verbose=False, return_history=False):model = LSTMDirect(input_size=1, hidden_size=hparams['hidden_size'],num_layers=hparams['num_layers'], dropout=hparams['dropout'], H=H).to(device)loss_fn = nn.MSELoss()opt = torch.optim.Adam(model.parameters(), lr=hparams['lr'], weight_decay=hparams.get('weight_decay',0.0))train_loader = DataLoader(TimeSeriesDataset(X_train_s, Y_train_s), batch_size=hparams['batch_size'], shuffle=True)val_loader = DataLoader(TimeSeriesDataset(X_val_s, Y_val_s), batch_size=hparams['batch_size'], shuffle=False)history = {'train_loss':[], 'val_loss':[]}best_val = float('inf'); best_state = None; patience=6; wait=0for ep in range(epochs):trl = train_one(model, opt, loss_fn, train_loader)vall, _, _ = evaluate(model, loss_fn, val_loader)history['train_loss'].append(trl); history['val_loss'].append(vall)if vall < best_val - 1e-8:best_val = vallbest_state = {k:v.cpu().clone() for k,v in model.state_dict().items()}wait = 0else:wait += 1if wait >= patience:breakmodel.load_state_dict(best_state)if return_history:return model, best_val, historyreturn model, best_val# 5. 简化贝叶斯优化（GP + EI）
space = {'hidden_size': (16, 128),'num_layers': (1, 3),'lr': (1e-4, 5e-2),'dropout': (0.0, 0.5),'batch_size': (16, 128)
}def sample_random_point():hs = int(np.round(np.random.uniform(space['hidden_size'][0], space['hidden_size'][1])))nl = int(np.round(np.random.uniform(space['num_layers'][0], space['num_layers'][1])))lr = 10**np.random.uniform(np.log10(space['lr'][0]), np.log10(space['lr'][1]))dr = np.random.uniform(space['dropout'][0], space['dropout'][1])bs = int(np.round(np.random.uniform(space['batch_size'][0], space['batch_size'][1])))bs = max(8, int(2**np.round(np.log2(bs))))return {'hidden_size':hs, 'num_layers':nl, 'lr':lr, 'dropout':dr, 'batch_size':bs}def vectorize_point(pt):return np.array([pt['hidden_size'], pt['num_layers'], np.log10(pt['lr']), pt['dropout'], pt['batch_size']])# 初始随机样本
np.random.seed(1)
init_n = 6
D_X = []; D_y = []; all_params = []for i in range(init_n):p0 = sample_random_point(); all_params.append(p0)_, val_loss = fit_model(p0, epochs=30, verbose=False)D_X.append(vectorize_point(p0)); D_y.append(val_loss)print("Init", i, "val_loss", val_loss, p0)D_X = np.vstack(D_X); D_y = np.array(D_y)
kernel = C(1.0, (1e-3, 1e3)) * Matern(length_scale=np.ones(D_X.shape[1]), nu=2.5) + WhiteKernel(noise_level=1e-6)
gp = GaussianProcessRegressor(kernel=kernel, normalize_y=True, n_restarts_optimizer=3, random_state=0)
gp.fit(D_X, D_y)
y_min = D_y.min()def expected_improvement(Xcand, gp, y_min, xi=0.01):mu, sigma = gp.predict(Xcand, return_std=True)sigma = np.maximum(sigma, 1e-9)Z = (y_min - mu - xi) / sigmaei = (y_min - mu - xi) * norm.cdf(Z) + sigma * norm.pdf(Z)return ei# BO 主循环：用随机候选采样来近似最大化获取函数
bo_iters = 18  # 可根据算力调小
for it in range(bo_iters):n_cand = 1200cand_pts = []; cand_vecs = []for _ in range(n_cand):pt = sample_random_point(); cand_pts.append(pt); cand_vecs.append(vectorize_point(pt))cand_vecs = np.vstack(cand_vecs)ei = expected_improvement(cand_vecs, gp, y_min, xi=0.01)best_idx = np.argmax(ei)next_pt = cand_pts[int(best_idx)]all_params.append(next_pt)_, val_loss = fit_model(next_pt, epochs=40, verbose=False)D_X = np.vstack([D_X, vectorize_point(next_pt)])D_y = np.concatenate([D_y, [val_loss]])gp.fit(D_X, D_y)y_min = D_y.min()print(f"BO iter {it+1}/{bo_iters}, val_loss={val_loss:.4f}, y_min={y_min:.4f}")# 取最优
best_idx = np.argmin(D_y)
best_vec = D_X[best_idx]
best_params = {'hidden_size': int(np.round(best_vec[0])),'num_layers': int(np.round(best_vec[1])),'lr': 10**best_vec[2],'dropout': float(best_vec[3]),'batch_size': int(np.round(best_vec[4]))
}
best_params['hidden_size'] = int(np.clip(best_params['hidden_size'], space['hidden_size'][0], space['hidden_size'][1]))
best_params['num_layers'] = int(np.clip(best_params['num_layers'], space['num_layers'][0], space['num_layers'][1]))
bs = max(8, int(2**np.round(np.log2(max(8, best_params['batch_size'])))))
best_params['batch_size'] = bs# 6. 用 train+val 重训最终模型
X_trainval = np.vstack([X_train, X_val]); Y_trainval = np.vstack([Y_train, Y_val])
scaler_x2 = StandardScaler().fit(X_trainval.reshape(-1,1))
scaler_y2 = StandardScaler().fit(Y_trainval.reshape(-1,1))
X_trainval_s = scaler_x2.transform(X_trainval.reshape(-1,1)).reshape(X_trainval.shape)
Y_trainval_s = scaler_y2.transform(Y_trainval.reshape(-1,1)).reshape(Y_trainval.shape)
X_test_s2 = scaler_x2.transform(X_test.reshape(-1,1)).reshape(X_test.shape)
Y_test_s2 = scaler_y2.transform(Y_test.reshape(-1,1)).reshape(Y_test.shape)def fit_final_model(hparams, epochs=120):model = LSTMDirect(input_size=1, hidden_size=hparams['hidden_size'],num_layers=hparams['num_layers'], dropout=hparams['dropout'], H=H).to(device)loss_fn = nn.MSELoss()opt = torch.optim.Adam(model.parameters(), lr=hparams['lr'], weight_decay=hparams.get('weight_decay',0.0))train_loader = DataLoader(TimeSeriesDataset(X_trainval_s, Y_trainval_s), batch_size=hparams['batch_size'], shuffle=True)test_loader = DataLoader(TimeSeriesDataset(X_test_s2, Y_test_s2), batch_size=256, shuffle=False)history = {'train_loss':[]}for ep in range(epochs):trl = train_one(model, opt, loss_fn, train_loader)history['train_loss'].append(trl)test_loss, test_preds, test_trues = evaluate(model, loss_fn, test_loader)test_preds_unscaled = scaler_y2.inverse_transform(test_preds.reshape(-1,1)).reshape(test_preds.shape)test_trues_unscaled = scaler_y2.inverse_transform(test_trues.reshape(-1,1)).reshape(test_trues.shape)return model, test_loss, test_preds_unscaled, test_trues_unscaled, historyfinal_model, test_loss, test_preds_unscaled, test_trues_unscaled, final_history = fit_final_model(best_params, epochs=120)# 7. MC Dropout 不确定性估计
def mc_dropout_preds(model, X_s, mc_runs=80):model.train()loader = DataLoader(TimeSeriesDataset(X_s, np.zeros((len(X_s), H))), batch_size=256, shuffle=False)preds = []with torch.no_grad():for _ in range(mc_runs):batch_preds = []for xb, _ in loader:xb = xb.to(device)p = model(xb).cpu().numpy()batch_preds.append(p)preds.append(np.vstack(batch_preds))preds = np.stack(preds, axis=0)mean = preds.mean(axis=0); std = preds.std(axis=0)return mean, stdmc_mean_s, mc_std_s = mc_dropout_preds(final_model, X_test_s2, mc_runs=60)
mc_mean = scaler_y2.inverse_transform(mc_mean_s.reshape(-1,1)).reshape(mc_mean_s.shape)
mc_std = scaler_y2.scale_[0] * mc_std_s# 8. 绘图
plt.rcParams['figure.figsize'] = (12,5)
# 图 A: 合成序列，强调 train/val/test 区域
fig, ax = plt.subplots(figsize=(14,4))
ax.plot(t, y, linewidth=1.0, label='Series', color='#ff6f61')
ax.axvspan(0, (train_end+p+H-1), alpha=0.12, color='#7fc97f', label='Train region')
ax.axvspan((train_end+p+H-1), (val_end+p+H-1), alpha=0.12, color='#fdc086', label='Val region')
ax.axvspan((val_end+p+H-1), T, alpha=0.12, color='#beaed4', label='Test region')
ax.set_title('Synthetic Time Series (trend + seasonality + spikes + noise)', fontsize=14)
ax.legend(); plt.tight_layout()# 图 B: BO 搜索过程（每次评估的 validation MSE）
fig, ax = plt.subplots(figsize=(12,4))
it_nums = np.arange(1, len(D_y)+1)
ax.plot(it_nums, D_y, marker='o', linewidth=1.5, label='Validation MSE per eval', color='#e41a1c')
ax.scatter(it_nums, D_y, c=D_y, cmap='viridis', s=60, edgecolor='k')
ax.set_xlabel('Evaluation #'); ax.set_ylabel('Validation MSE'); ax.set_title('BO: validation loss per eval', fontsize=14)
ax.grid(alpha=0.25); ax.set_yscale('log'); plt.tight_layout()# 图 C: 超参数采样散点（hidden_size vs lr），色彩映射为 val loss
fig, ax = plt.subplots(figsize=(10,6))
vecs = D_X; vals_plot = D_y
sc = ax.scatter(vecs[:,0], 10**vecs[:,2], c=vals_plot, s=90, cmap='plasma', edgecolor='k')
ax.set_yscale('log'); ax.set_xlabel('hidden_size'); ax.set_ylabel('learning_rate (log)'); ax.set_title('Hyperparameter samples colored by val MSE', fontsize=14)
cb = plt.colorbar(sc, ax=ax); cb.set_label('Validation MSE'); plt.tight_layout()# 图 D: 单个测试窗口的 history + 真值 + 预测与 95% CI
sel_idx = 30
true_hist = X_test[sel_idx]; true_future = Y_test[sel_idx]
pred_mean = mc_mean[sel_idx]; pred_std = mc_std[sel_idx]
fig, ax = plt.subplots(figsize=(12,5))
ax.plot(np.arange(p), true_hist, label='History', linewidth=2, color='#377eb8')
ax.plot(np.arange(p, p+H), true_future, label='True future', linewidth=2, color='#4daf4a')
ax.plot(np.arange(p, p+H), pred_mean, label='Pred mean (MC Dropout)', linewidth=2, color='#ff7f00')
ax.fill_between(np.arange(p, p+H), pred_mean - 1.96*pred_std, pred_mean + 1.96*pred_std, alpha=0.35, color='#ff7f00', label='95% CI')
ax.scatter(np.arange(p, p+H), pred_mean, s=60, color='#ff7f00', edgecolor='k')
ax.set_title('One test-window: history, true future and predicted (95% CI)', fontsize=14); ax.legend(); plt.tight_layout()# 图 E: 最终重训的训练 loss 曲线
fig, ax = plt.subplots(figsize=(10,4))
ax.plot(final_history['train_loss'], label='Train loss (final retrain)', color='#984ea3', linewidth=1.6)
ax.set_xlabel('Epoch'); ax.set_ylabel('MSE'); ax.set_title('Final model training loss (retrain on train+val)', fontsize=14); ax.grid(alpha=0.2); plt.tight_layout()# 图 F: 测试集中一段窗口的 first-step 对比（多窗口并列）
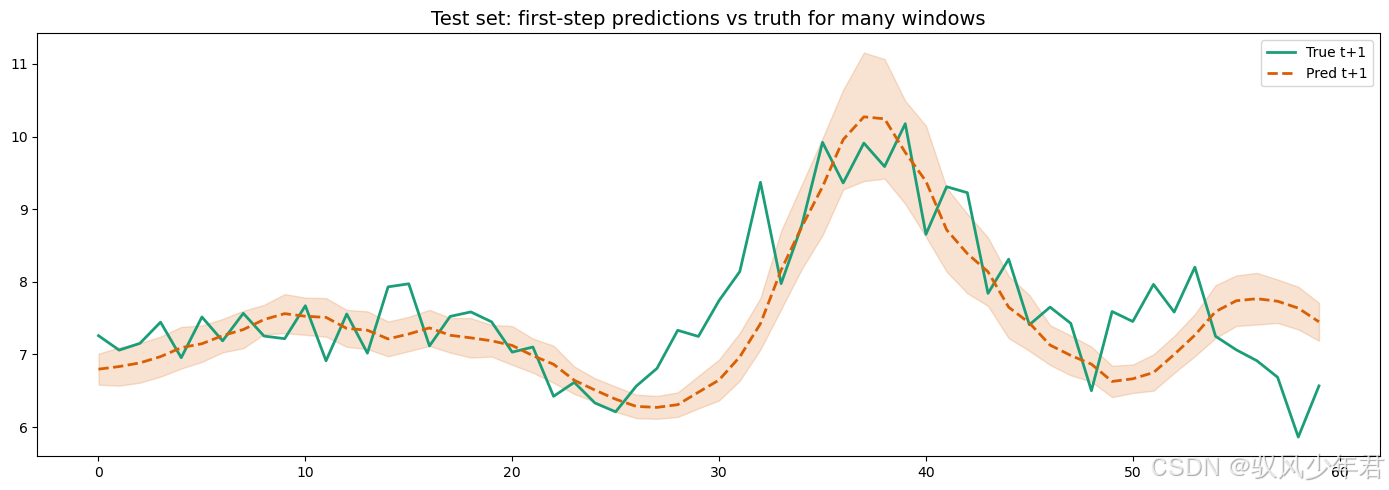
fig, ax = plt.subplots(figsize=(14,5))
nplot = 60
x_axis = np.arange(nplot)
ax.plot(x_axis, test_trues_unscaled[:nplot,0], label='True t+1', color='#1b9e77', linewidth=2)
ax.plot(x_axis, test_preds_unscaled[:nplot,0], label='Pred t+1', color='#d95f02', linewidth=2, linestyle='--')
ax.fill_between(x_axis, (test_preds_unscaled[:nplot,0]-1.96*mc_std[:nplot,0]), (test_preds_unscaled[:nplot,0]+1.96*mc_std[:nplot,0]), color='#d95f02', alpha=0.18)
ax.set_title('Test set: first-step predictions vs truth for many windows', fontsize=14); ax.legend(); plt.tight_layout()plt.show()# 最后打印 summary
print("Best params (rounded):", best_params)
print("Best validation MSE (GP observed):", float(D_y.min()))
print("Final test MSE (scaled-space):", float(test_loss))

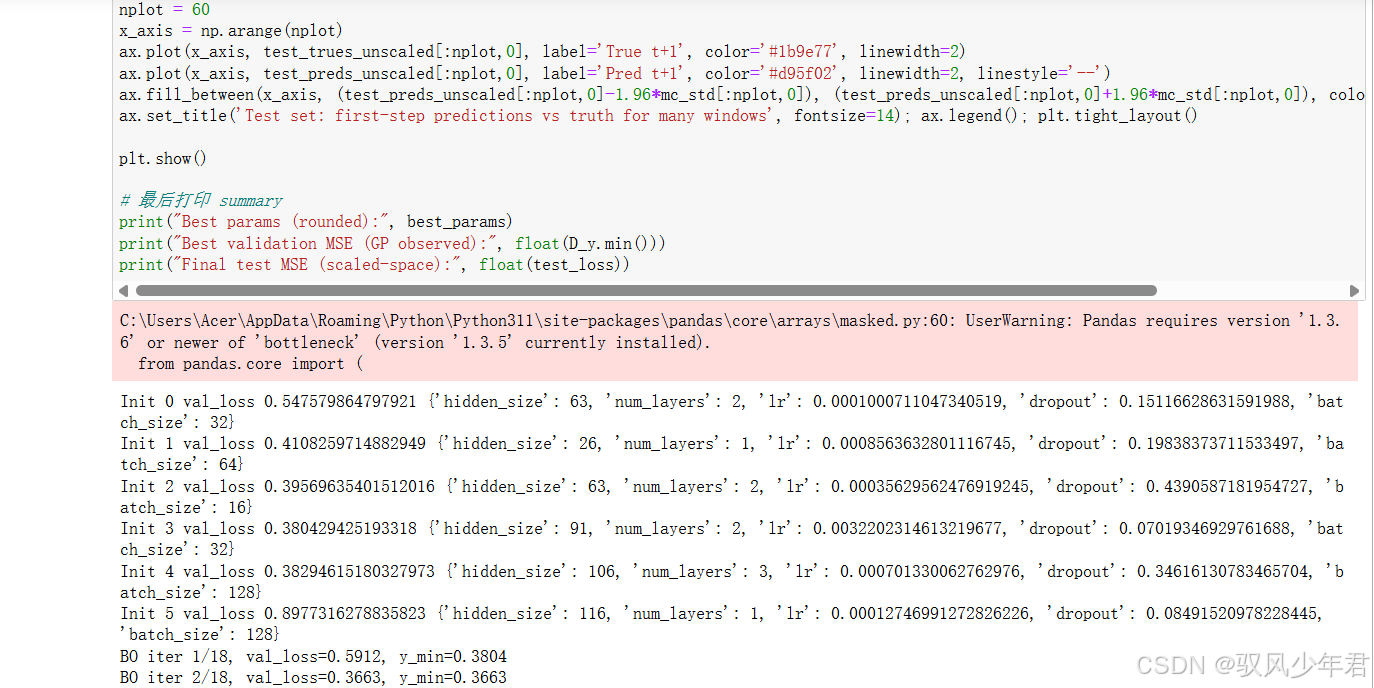
Init 0 val_loss 0.547579864797921 {'hidden_size': 63, 'num_layers': 2, 'lr': 0.0001000711047340519, 'dropout': 0.15116628631591988, 'batch_size': 32}
Init 1 val_loss 0.4108259714882949 {'hidden_size': 26, 'num_layers': 1, 'lr': 0.0008563632801116745, 'dropout': 0.19838373711533497, 'batch_size': 64}
Init 2 val_loss 0.39569635401512016 {'hidden_size': 63, 'num_layers': 2, 'lr': 0.00035629562476919245, 'dropout': 0.4390587181954727, 'batch_size': 16}
Init 3 val_loss 0.380429425193318 {'hidden_size': 91, 'num_layers': 2, 'lr': 0.0032202314613219677, 'dropout': 0.07019346929761688, 'batch_size': 32}
Init 4 val_loss 0.38294615180327973 {'hidden_size': 106, 'num_layers': 3, 'lr': 0.000701330062762976, 'dropout': 0.34616130783465704, 'batch_size': 128}
Init 5 val_loss 0.8977316278835823 {'hidden_size': 116, 'num_layers': 1, 'lr': 0.00012746991272826226, 'dropout': 0.08491520978228445, 'batch_size': 128}
BO iter 1/18, val_loss=0.5912, y_min=0.3804
BO iter 2/18, val_loss=0.3663, y_min=0.3663
BO iter 3/18, val_loss=0.4171, y_min=0.366
...
BO iter 18/18, val_loss=0.4265, y_min=0.3663