当前位置：首页 > news >正文

2025牛客暑期多校训练营4(FBDGI)

news 2025/9/4 10:58:00

题目链接：牛客竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ

F.For the Treasury!

思路

最终我们要使得 $a_{x_1} a_{x_2}...a_{x_k}$ 作为前k个而进行答案统计，其中 $x_1<x_2<...<x_k$ 那么最终的利润为 $\sum_{i=1}^{k}a_{x_i}-(x_i-i)*c$

整理一下公式可得到，我们只需要对 $a_i-i*c$ 排序取前k个大的求和然后加上 $\frac{(k+1)*k}{2}*c$ 即可

代码

void solve(){int n,k,c;cin>>n>>k>>c;vi a(n+1);for(int i=1;i<=n;i++){int x;cin>>x;a[i]=x-c*i;}sort(a.begin()+1,a.begin()+1+n,greater<int>());int ans=0;for(int i=1;i<=k;i++){ans+=a[i];}ans=ans+(k*(k+1)/2)*c;cout<<ans<<"\n";
}

B.Blind Alley

思路

1.从(1,1)出发只能向右和上下移动所能到达的点

2.从(1,m)出发只能向左和上下移动所能到达的点

我们找到1能到达的点，而2不能到达的点，从此点出发探寻其深度是否能够>=k

代码

#include<bits/stdc++.h>
using namespace std;#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); 
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;vector<vector<int>> d1={{0,1},{1,0},{-1,0}};
vector<vector<int>> dm={{0,-1},{1,0},{-1,0}};void solve(){int n,m,k;cin>>n>>m>>k;vector<vector<char>> g(n+5,vector<char>(m+5));for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>g[i][j];}}vector<vector<bool>> vis1(n+5,vector<bool>(m+5,false));     //从(1,1)出发可到达的点为truevector<vector<bool>> vism(n+5,vector<bool>(m+5,false));     //从(1,m)出发不可到达的点为falseauto dfs=[&](auto self,int x,int y,vector<vector<int>> d,vector<vb>&vis)->void{vis[x][y]=true;for(int i=0;i<3;i++){int xx=x+d[i][0];int yy=y+d[i][1];if(xx<1||yy<1||xx>n||yy>m||g[xx][yy]=='1'||vis[xx][yy]) continue;self(self,xx,yy,d,vis);}};dfs(dfs,1,1,d1,vis1);dfs(dfs,1,m,dm,vism);//从(1,1)能到达而(1,m)不能到达的点出发看其到达的深度是否>=kint mx=0;vector<vb> tvis(n+5,vb(m+5,false));auto tdfs=[&](auto self,int x,int y,vector<vector<int>> d,vector<vb>&vis)->void{mx=max(mx,y);vis[x][y]=true;for(int i=0;i<3;i++){int xx=x+d[i][0];int yy=y+d[i][1];if(xx<1||yy<1||xx>n||yy>m||g[xx][yy]=='1'||vis[xx][yy]) continue;self(self,xx,yy,d,vis);}};for(int j=1;j<=m;j++){for(int i=1;i<=n;i++){if(g[i][j]=='0'&&vis1[i][j]&&!vism[i][j]){tdfs(tdfs,i,j,d1,tvis);if(mx-j+1>=k){cout<<"YES\n";return;}}}}cout<<"NO\n";
}
signed main() {vcoistntcout<<fixed<<setprecision(2);int _=1;cin>>_;while(_--) solve();return 0;
}

D.Determinant of 01-Matrix

思路

行列式没学好的有福了，此题官方题解构造的非常巧妙，建议看一下官方题解~~(因为我行列式没有学好)~~

代码

#include<bits/stdc++.h>
using namespace std;#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); 
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;const int N=207;
const int B=30;
int a[N][N];
int b[4][5]={{1,1,0,0,0},{0,1,1,0,0},{1,0,1,1,0},{0,0,0,1,1}};void solve(){int L=1,R=0;for (int t=0;t<B;++t){for (int i=0;i<4;++i){for (int j=0;j<5;++j){a[L+i][R+j]=b[i][j];}}L+=4, R+=4;}int n;cin>>n;for (int i=0;i<30;++i){if (n>>i&1) a[0][4*i]=1; }cout<<4*B<<"\n";for (int i=0;i<4*B;++i){for (int j=0;j<4*B;++j){cout<<a[i][j]<<" ";}cout<<"\n";}
}
signed main() {vcoistntcout<<fixed<<setprecision(2);int _=1;
//     cin>>_;while(_--) solve();return 0;
}

G.Ghost in the Parentheses

思路

这个题也是很有意思的

考虑将‘(’看成+1，')'看成-1，用f[i]表示前缀和，要满足此字符串是合法的要满足

1.所有的f[i]>=0

2.f[n]=0，f[1]=1

3.n为偶数且'('和‘)’各为一半

考虑如何得到确切的字符串，即'('与‘)’交换后字符串就不合法了，此时可以将f数组的值作为折线图画出来

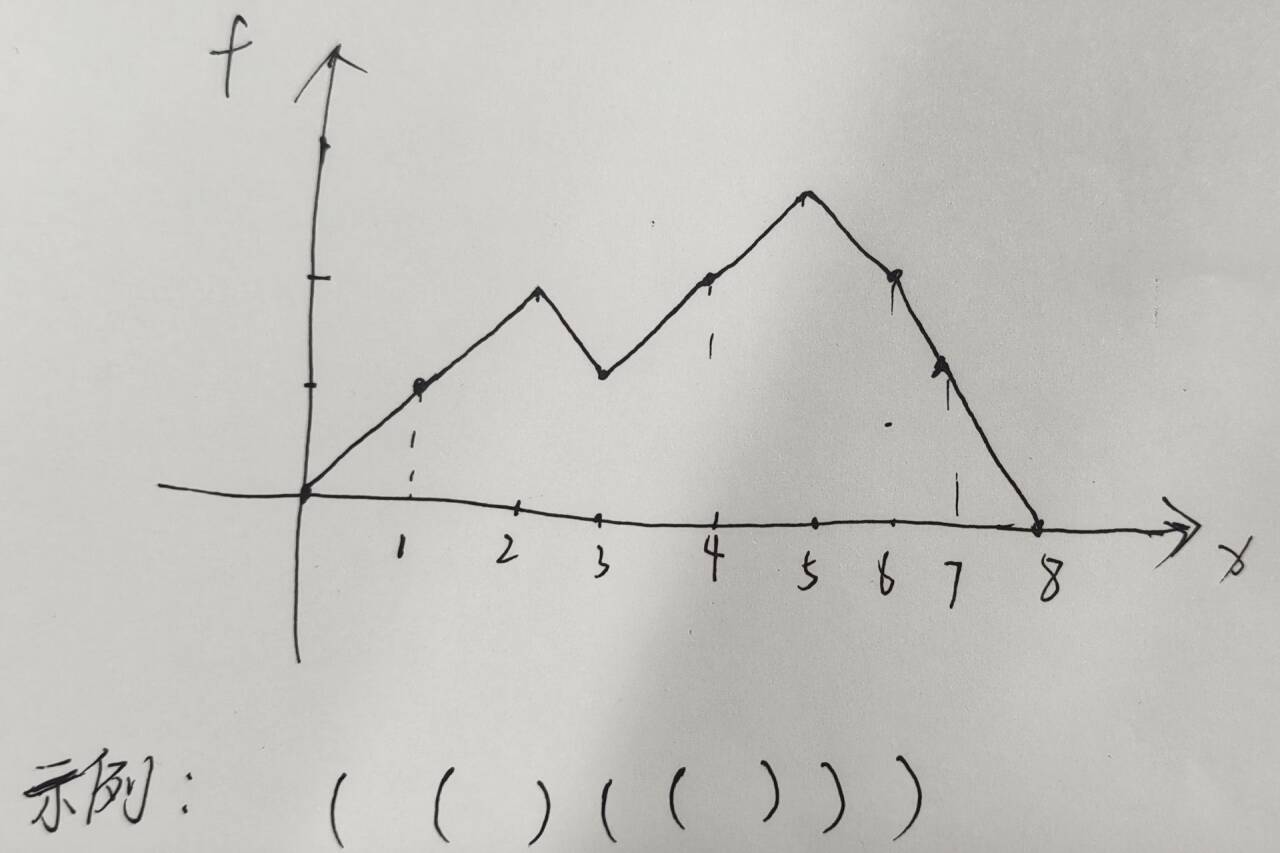
一、...）...（...交换，如图所示，依然合法，也就是说我们将两个如果都变成？的话那么这个字符串就一定是不确定的，所以我们应当至少保留一个

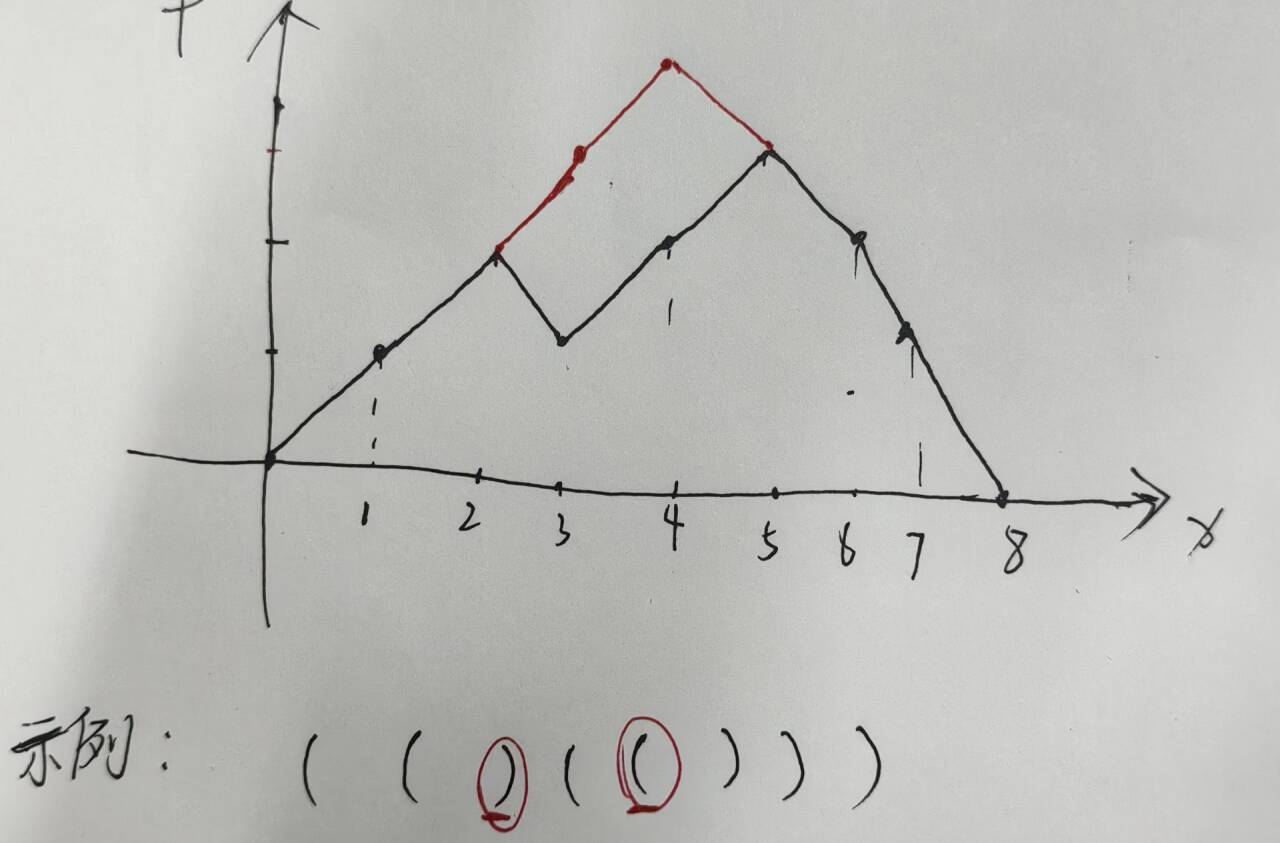
二、....（....）...交换，同理我们假设交换位置为a和b，我们需要保证[a,b]内的f[i]的值必须是>2的最终字符串才可以是合法的，也就是我们要保证字符串是确切的第一个'('变成？的情况下直到第一个f[i]<2内的')'都可以变成？

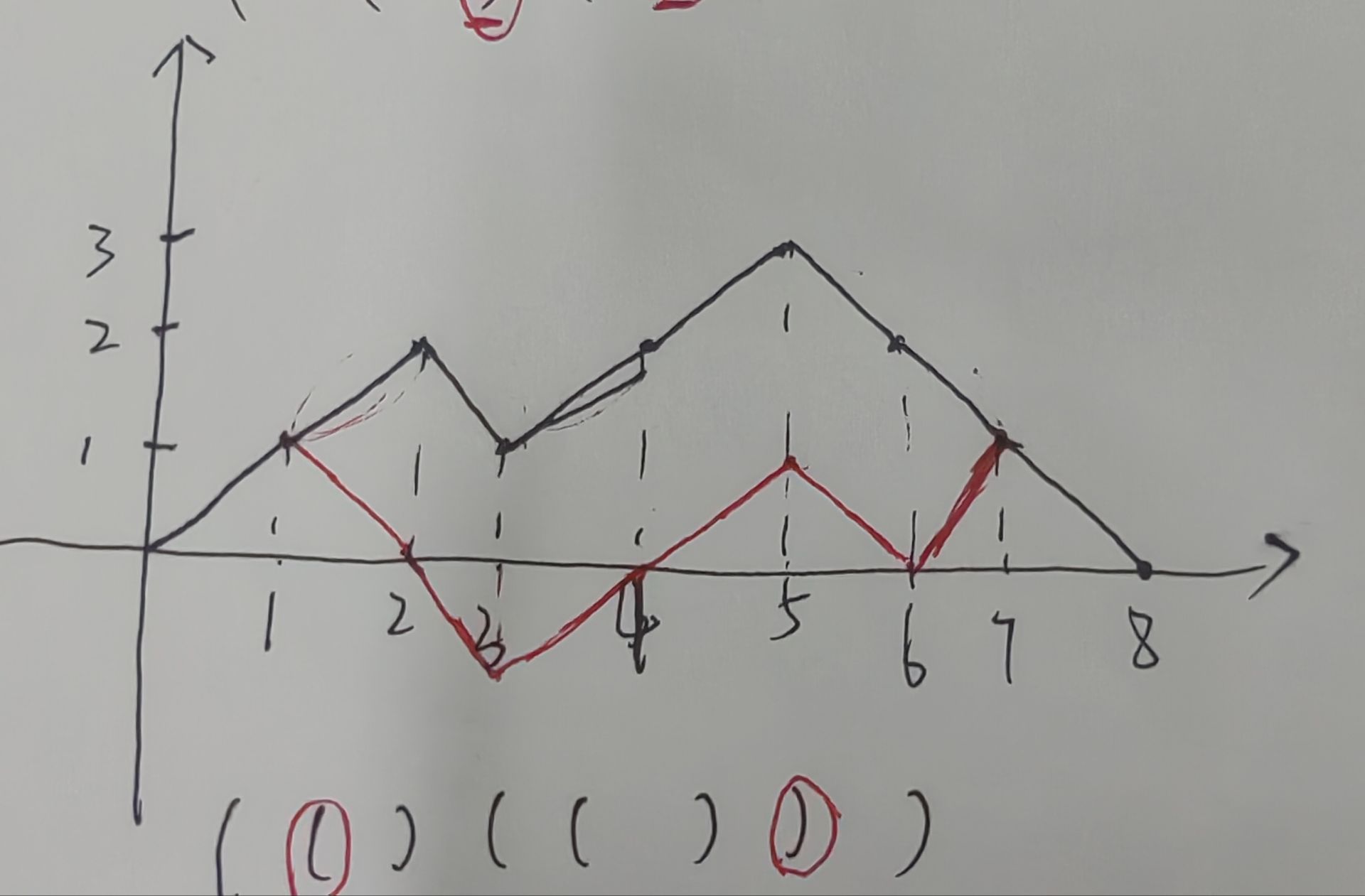
那么综上所述，考虑枚举最后一个变成？的‘(’，答案便是 $(\frac{1}{2})^{pre[r[i]]+suf[i+1]+1}$ ,其中pre[i]为i之前‘)’的数量，suf[i]为i及之后'('的数量，r[i]为i之后第一个f[i]<2的位置，注意不要忘记'('全部为？‘)’全部保留的情况

代码

#include<bits/stdc++.h>
using namespace std;#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); 
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;int qpow(int a,int b){int ans=1;while(b){if(b&1){ans=(ans*a)%mod;}a=((a%mod)*(a%mod))%mod;b>>=1;}return ans;
}
int inverse(int a){return qpow(a,mod-2);
}void solve(){string s;cin>>s;int n=s.size();s=" "+s;vi f(n+1,0);for(int i=1;i<=n;i++){f[i]=f[i-1];if(s[i]=='(') f[i]++;else f[i]--;}vi pre(n+1,0);  //i及之前')'的数量vi suf(n+2,0);  //i及之后'('的数量for(int i=1;i<=n;i++){pre[i]=pre[i-1];if(s[i]==')') pre[i]++;}for(int i=n;i>=1;i--){suf[i]=suf[i+1];if(s[i]=='(') suf[i]++;}vi r(n+1);  //i之后第一个f[i]<2的位置int R=n;for(int i=n;i>=1;i--){if(f[i]<2) R=i;r[i]=R;}int ans=0;ans=(ans+inverse(qpow(2,n/2)))%mod;for(int i=1;i<=n;i++){  //枚举最后一个失效的'('if(s[i]=='('){ans=(ans+inverse(qpow(2,pre[r[i]]+suf[i+1]+1)))%mod;}}cout<<ans<<"\n";
}
signed main() {vcoistntcout<<fixed<<setprecision(2);int _=1;// cin>>_;while(_--) solve();return 0;
}

I.I, Box

思路

此题感觉思路倒是不难

‘#’将所有的问题分成多个连通块，每个连通块内箱子和目标节点必须得是成对出现的，对于每个连通块，我们让任意的箱子和目标节点匹配即可，移动箱子的过程中如果中途碰到箱子我们让此路线的最后一个箱子代替原来的箱子即可

代码

#include<bits/stdc++.h>
using namespace std;#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL); 
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;const int dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
const char ch[4]={'R','L','D','U'};struct node{int x,y;char c;
};void solve(){int n,m;cin>>n>>m;vector<vector<char>> g(n+1,vector<char>(m+1));for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>g[i][j];}}vector<node> ans;vector<vector<bool>> vis;auto dfs=[&](auto self,int x,int y)->bool{if(g[x][y]=='*'){g[x][y]='!';return true;}vis[x][y]=true;for(int i=0;i<4;i++){int xx=x+dir[i][0];int yy=y+dir[i][1];if(xx<1||xx>n||yy<1||yy>m||vis[xx][yy]||g[xx][yy]=='#') continue;if(g[xx][yy]=='.'){ans.push_back({x,y,ch[i]});if(self(self,xx,yy)) return true;ans.pop_back();}else{if(self(self,xx,yy)){ans.push_back({x,y,ch[i]});return true;}}}return false;};for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(g[i][j]=='@'){vis=vector<vector<bool>>(n+1,vb(m+1,false));if(dfs(dfs,i,j)){g[i][j]='.';}else{cout<<"-1\n";return;}}}}cout<<ans.size()<<"\n";for(auto tmp:ans){cout<<tmp.x<<" "<<tmp.y<<" "<<tmp.c<<"\n";}
}
signed main() {vcoistntcout<<fixed<<setprecision(2);int _=1;// cin>>_;while(_--) solve();return 0;
}

查看全文

http://www.dtcms.com/a/363459.html