LabVIEW振动信号积分处理
该系统围绕振动信号(加速度),通过积分操作获取速度、位移,结合仿真信号设置与多图可视化,分析振动特性,利用积分对高频信号的相对衰减作用,优化信号处理。
积分在振动信号处理中,可将加速度信号依次积分得到速度、位移信号,且能相对衰减高频信号,使低频信号更突出,便于分析振动的时变特性与趋势。
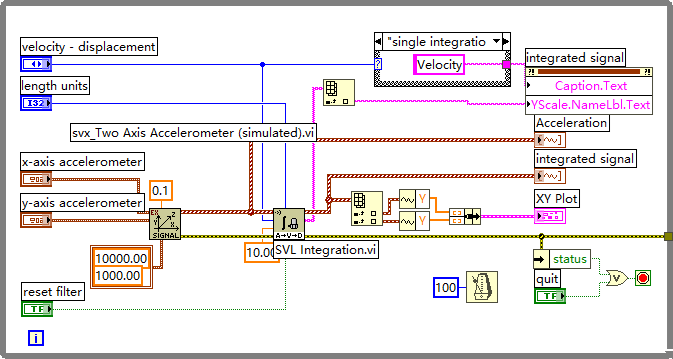
“Simulated Signal” 相关设置
功能:配置仿真振动信号的参数,如基频、振幅、相位、谐波等,生成符合需求的振动信号。
复杂信号生成操作:在 “Simulated Signal Settings” 区域,针对复杂振动多基频、多谐波、相位关系复杂等特点,细致设置x、y轴加速度计参数。若复杂振动由多个基础频率成分叠加,可分别为x、y轴设置不同基频;根据实际复杂振动中各频率成分的强弱,调整不同频率对应的振幅;通过设置不同相位值,模拟相位差对振动合成的影响;选择 “odd only” 或其他谐波类型,设置合适的谐波数量,生成包含丰富谐波成分的复杂振动信号,贴近实际中含有谐波失真的振动场景。
使用场合:在无实际振动信号或需模拟特定振动场景(如不同谐波成分的振动)时使用。
特点:参数可调性强,能灵活生成多种振动信号,满足不同分析需求。
使用注意事项:需依据实际振动场景合理设置参数,保证仿真信号的真实性与针对性。
对比类似功能:与 “Real Signal Acquisition”(实际信号采集,从传感器获取真实信号)相比,它无需实际硬件采集,可快速生成模拟信号用于算法验证等,但缺乏真实信号的复杂性与随机性。
积分处理
功能:对输入信号(如加速度)执行单次积分,得到速度信号,多次积分可获取位移信号。
复杂信号积分操作:复杂振动信号中,高频成分往往包含较多噪声或非关键信息,而积分具有相对衰减高频信号的特性。通过 “Single Integration”,可突出低频的、更能反映振动趋势的成分,同时得到速度、位移这些不同维度的振动描述,丰富分析视角。若需要从加速度直接得到位移,可进行两次积分操作(系统支持 “double integration” 模式时,可启用该功能快速实现)。
使用场合:需从加速度信号获取速度、位移信息的场景,如复杂振动过程的速度、位移分析。
特点:操作简洁,针对性强,专注积分转换。
使用注意事项:输入信号需确保采样率等参数适配,避免积分误差积累。
对比类似功能:与 “Double Integration”(双积分,直接从加速度到位移)相比,它仅完成一次积分,步骤更单一,适用于只需速度信号的情况,而双积分更侧重最终位移获取,积分次数多,误差相对更易累积。
“XY Plot” VI
功能:实现信号的 XY 平面绘图,可将不同维度信号(如 X、Y 方向振动)关联展示。
复杂信号可视化操作:将x、y轴经积分等处理后的信号(如速度 - 速度、位移 - 位移或速度 - 位移组合)进行 XY 绘图,分析复杂振动在平面上的轨迹、相关性,比如判断振动是否存在椭圆轨迹、螺旋轨迹等复杂形态,进而推断振动源的特性(如旋转机械的不对中、不平衡等故障会产生特定的 XY 轨迹)。同时,结合 “Signal Data” 区域,观察加速度、位移随时间的变化曲线,分析不同时刻各振动参数的数值变化、波动规律,判断是否存在周期性、冲击性等复杂特征。
使用场合:分析多维度振动信号的相关性、轨迹等场景,如旋转机械的振动轨迹分析。
特点:直观呈现信号间的空间或关联关系,便于发现信号间的复杂模式。
使用注意事项:需确保输入的 X、Y 信号数据长度匹配,否则绘图会出错。
对比类似功能:与普通 “Time Plot”(时间域绘图,单信号随时间变化)相比,它聚焦多信号的关联绘图,能展现信号间的相互作用,而时间域绘图更侧重单信号的时序特性。
复杂振动信号分析处理
信号仿真生成:按复杂振动多频率、多谐波等特点,在 “Simulated Signal Settings” 细致设置参数,生成模拟信号。
积分处理:利用积分衰减高频、获取速度 / 位移信号,丰富分析维度。
多维度可视化分析:通过 “Signal Data” 和 “XY Plot” 观察信号时序与关联特性。
参数调整与迭代优化:根据分析结果,微调仿真、积分等参数,结合滤波(借助 “reset filter”)优化,直至准确反映复杂振动特性。
