【洛谷】【模板】栈、有效的括号、验证栈序列、后缀表达式、(stack相关算法题)

---

【模板】栈

题目描述

题目解析

这道题非常简单，唯一需要注意的是x的数据范围，我们知道无论是32位还是64位：
int 通常占 4 字节，取值范围为：(-2^31到2^31 - 1)；
unsigned int也占 4 字节，取值范围为：(0到 2^32 - 1)；
long long通常占 8字节，取值范围为：(-2^63到 2^63 - 1)；
unsigned long long也占 8 字节，取值范围为：(0到 2^64 - 1)；
所以这里我们使用unsigned long long就刚好符合题目对x数据范围的规定。

代码

因为本题不涉及复杂过程，推荐使用第二种方法用数组模拟栈，效率更高。

using namespace std;
#include <iostream>
#include <stack>typedef unsigned long long ULL;size_t T;
size_t n;int main()
{cin >> T;for (int i = 0; i < T; i++){cin >> n;stack<ULL> st;for (int j = 0; j < n; j++){string str;cin >> str;if (str == "push"){ULL x;cin >> x;st.push(x);}else if (str == "pop"){if (st.empty())cout << "Empty" << endl;elsest.pop();}else if (str == "query"){if (st.empty())cout << "Anguei!" << endl;elsecout << st.top() << endl;}else{cout << st.size() << endl;}}}return 0;
}//用数组模拟栈
using namespace std;
#include <iostream>typedef unsigned long long ULL;const int N = 1e6 + 10;
ULL st[N];
int T;
int n;int main()
{int top = 0; //指向栈顶cin >> T;for (int i = 0; i < T; i++){cin >> n;top = 0;  //一组数据开始之前先清楚原先栈的数据for (int j = 0; j < n; j++){string str;cin >> str;if (str == "push"){ULL x;cin >> x;st[++top] = x;}else if (str == "pop"){if (top == 0)cout << "Empty" << endl;else--top;}else if (str == "query"){if (top == 0)cout << "Anguei!" << endl;elsecout << st[top] << endl;}else{cout << top << endl; //数组是从下标1开始存的}}}return 0;
}

有效的括号

题目描述

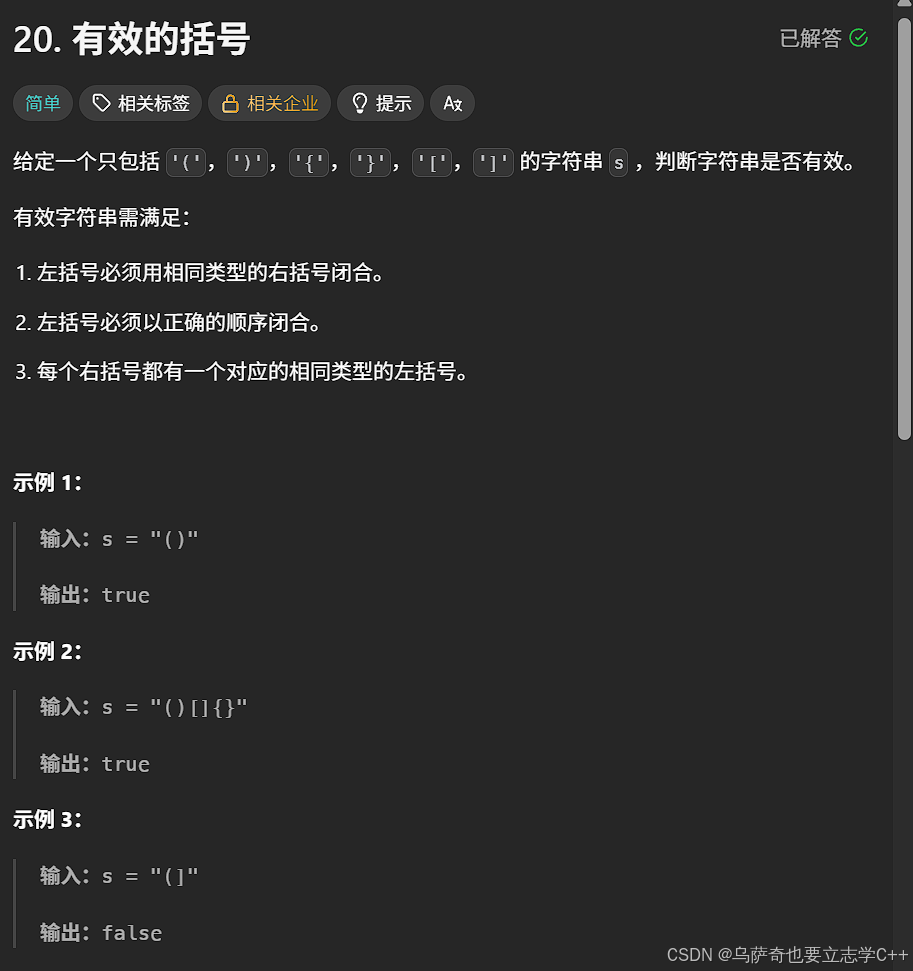
题目解析

这道题思路很简单，看下面的代码注释。注意细节右两个：
1、遇到右括号时若栈为空，无法匹配，返回false。(例如只有一个右括号，返回false)
2、遍历完string出循环后需要判断栈是否为空，若为空表示全部元素匹配成功返回ture，否则返回false。(例如只有一个左括号，返回false)

代码

class Solution {
public:bool isValid(string s) {stack<char> st;for(auto e : s){//遇到左括号入栈if(e == '(' || e == '[' || e == '{')st.push(e);//遇到右括号与栈顶元素比较else{//若此时栈中无元素，无法匹配if(st.empty())return false;//匹配失败，返回falseelse if((e == ')' && st.top() != '(') || (e == ']' && st.top() != '[') || (e == '}' && st.top() != '{')) return false;//匹配成功，pop栈顶，继续循环比较else              st.pop();}}//若遍历完后若栈为空,返回true，否则falsereturn st.empty();}
};

验证栈序列

题目描述

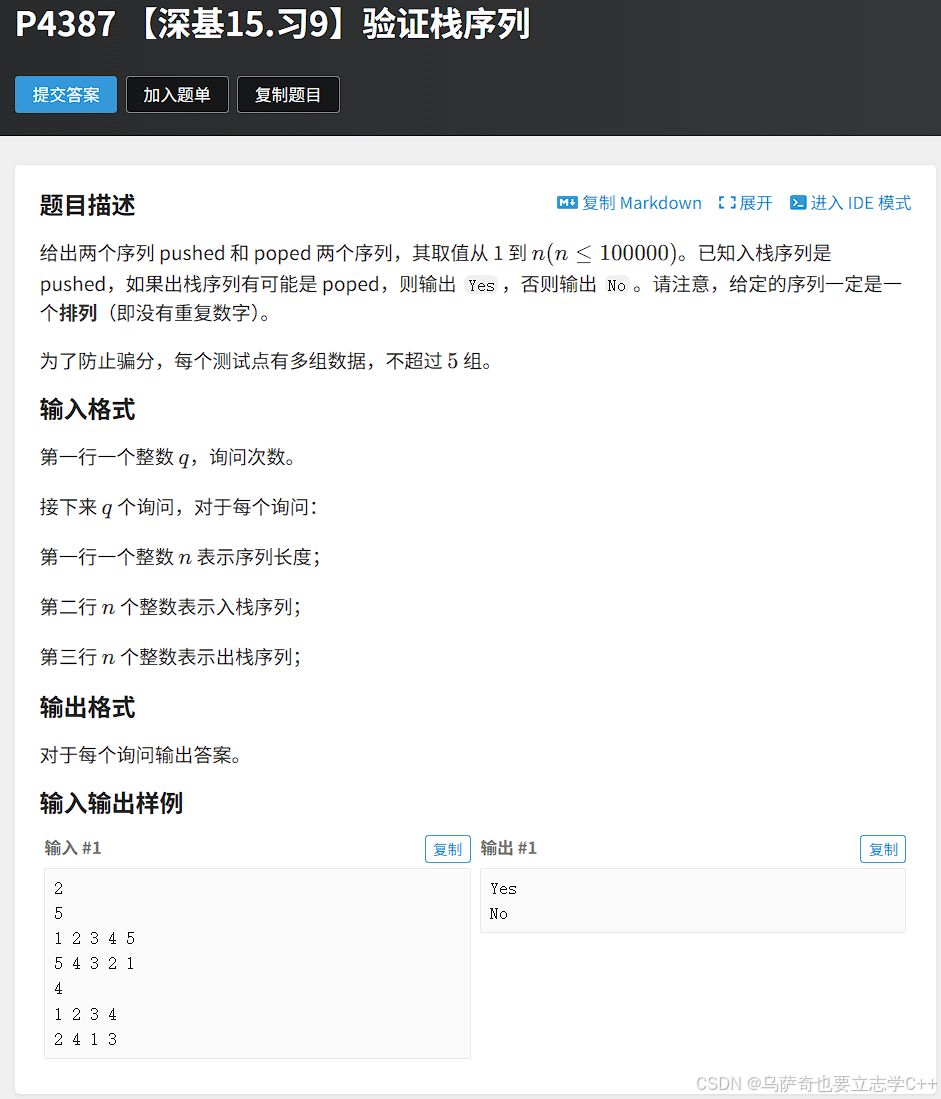
题目解析

这道题很经典，思路就是创建一个栈来模拟验证入栈序列和出栈序列是否匹配，需要注意的点是模拟数组出栈，并判断出栈数据是否和出栈序列匹配时while循环的条件要加一个j >= n，避免出栈序列数组越界访问。

代码

using namespace std;
#include <iostream>
#include <stack>
#include <string>const int N = 1e5 + 10;
int push[N]; //存放入栈序列
int pop[N];  //存放出栈序列
int q;
int n;int main()
{cin >> q;//询问q轮while (q--){//根据输入创建入栈和出栈序列数组cin >> n; //系列长度for (int i = 1; i <= n; i++){cin >> push[i];}for (int i = 1; i <= n; i++){cin >> pop[i];}int j = 1; //j指向出栈序列下标stack<int> st;//遍历入栈序列验证和出栈序列是否匹配//i始终指向入栈序列下标for (int i = 1; i <= n; i++){//不管如何，先把数据入栈st.push(push[i]);//若此时栈顶数据和出栈序列下标为j的元素相等,开始出栈匹配while (!st.empty() && j <= n && st.top() == pop[j]) {//模拟数组出栈，并判断出栈数据是否和出栈序列匹配st.pop();++j;}}if (st.empty()){//匹配完后栈为空，表示匹配成功cout << "Yes" << endl;}else{//匹配完后栈不为空，表示匹配失败cout << "No" << endl;}}return 0;
}

后缀表达式

题目描述

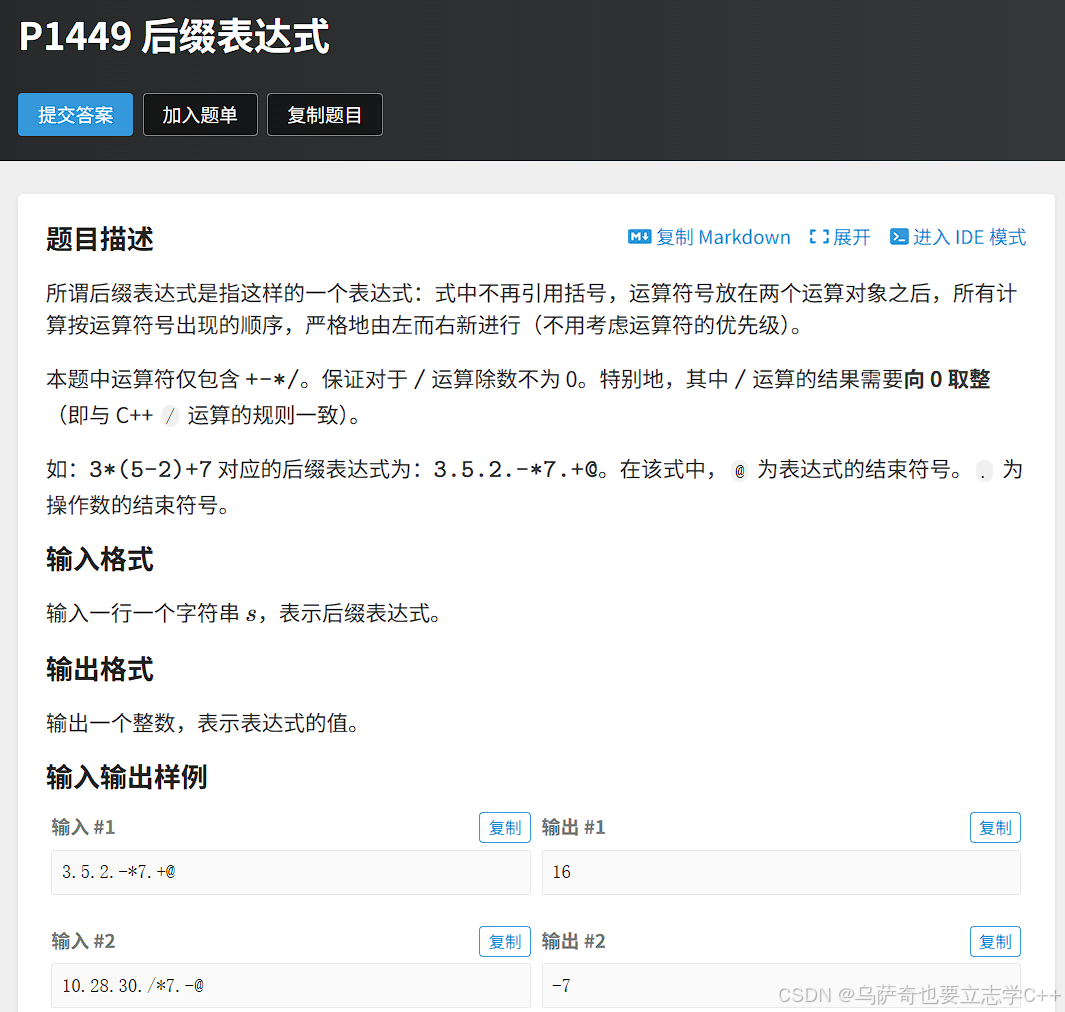
题目解析

这道题也很经典，核心思路是遇到数字把数字入栈，遇到运算符弹出栈顶两个数字，栈顶数字当作左操作数，第二个数字当作右操作数，运算后把结果重新入栈。
但是这道题有一个细节，数值大小不是直接给的，而是给的一串字符串，需要我们自己从字符串中提取数字字符并转换为数值。解决这个思路有两种方法，第一种可能是大家最先想到的，先通过 numstr += e 拼接字符，遇到 . 后逆序遍历字符串，并通过位权计算数值，这种方法需要字符串动态扩容有额外开销，所以我们更推荐第二种方法，直接算术累积，这里会用到秦九韶算法的思想，它是一种高效计算多项式值的算法，运用到本道题的思路就是“前一次结果 × 10 + 当前位数字” ，下面小编以129为例给大家演示一下：

代码

//思路1
using namespace std;
#include <iostream>
#include <stack>
#include <string>int main()
{string str;cin >> str;stack<int> st;string numstr; //暂存数字字符串for (auto e : str){//若遇到数字字符把数字字符存到numstrif(e >= '0' && e <= '9'){//numstr += e;}//若遇到'.'，把数字字符串转化为数字入栈，并把numstr置空else if (e == '.'){int num = 0;  //转化后入栈数字int quan = 1; //位权//从个位开始遍历numstr，个位权为1，十位权为10，依次类推//计算前需要把数字字符转化为数值auto it = numstr.rbegin();while (it != numstr.rend()){//数字字符‘0’的ASCII码值为48num += (*it - '0') * quan;quan *= 10;it++;}st.push(num);numstr.clear();}//若遇到运算符把栈顶两个数据出栈，把栈顶数据当作右操作数，// 栈顶第二个数据当作左操作数，运算后把结果重新入栈else if (e == '+' || e == '-' || e == '*' || e == '/'){int b = st.top();st.pop();int a = st.top();st.pop();int c = 0;  //运算结果if (e == '+')c = a + b;else if(e == '-')c = a - b;else if (e == '*')c = a * b;elsec = a / b;st.push(c);}//遇到‘@’，退出范围forelse{break;}}//把栈里剩余的一个数据当作结果输出int ret = st.top();cout << ret;return 0;
}//思路2
using namespace std;
#include <iostream>
#include <stack>int main()
{stack<int> st;char e; //存放输入的字符int num = 0; //存放数字字符串转换后的数值while (cin >> e){if (e == '@')break;else if (e >= '0' && e <= '9'){//秦九韶算法num = num * 10 + (e - '0');}else if (e == '.'){st.push(num);num = 0; //num置0}else{int b = st.top(); //左操作数st.pop();int a = st.top(); //右操作数st.pop();int c = 0;  //运算结果if (e == '+')c = a + b;else if (e == '-')c = a - b;else if (e == '*')c = a * b;elsec = a / b;st.push(c);}}cout << st.top();return 0;
}

括号序列

题目描述

题目解析

解答本题要用到前面有效的括号题目的思路。
第一步和有效的括号类似，先遍历整个字符串，只不过这里会多一个步骤，需要标记当前字符是否匹配成功，所以需要一个bool数组st存放字符的标记值，数组st的下标和字符串str的下标一一对应，若某个字符匹配成功，就在st数组对应的下标位置置为true,因为数组st里的元素默认是false，如果匹配不成功则不做任何处理。
第二步再次遍历整个字符串，并创建一个新字符串ret用于存放配对完后的结果。遍历原字符串，若遇到字符的标记为true，直接插入ret，若不为true，则识别当前字符是那个具体括号，手动添加与之匹配的括号。
最后范围for输出字符串ret的结果就行了。

代码

using namespace std;
#include <iostream>
#include <stack>
#include <string>const int N = 110;
//用该数组下标标记字符串哪些位置的字符匹配成功
bool st[N]; //st数组定义在全局，值全被初始化为falseint main()
{string str;cin >> str;stack<int> stk; //栈存储字符串下标//遍历整个字符串for (int i = 0; i < str.size(); i++){char ch = str[i];//遇到左括号把左括号下标入栈if (ch == '(' || ch == '['){stk.push(i);}//遇到右括号与栈顶元素匹配//匹配成功的两个位置标记为trueelse{//若这时栈为空，无法匹配，让该位置保持falseif (stk.empty()){continue;}//top为栈顶字符元素下标int top = stk.top();//char为栈顶字符元素char left = str[top];//匹配成功if ((ch == ')' && left == '(') ||(ch == ']' && left == '[')){st[i] = st[top] = true;stk.pop();}//若未匹配成功，让st[i]、st[top]保持false}}//遍历字符串str，给未配对的括号配对string ret; //用于维护配对完后的字符串for (int j = 0; j < str.size(); j++){char ch = str[j];if (st[j] == true){//若该字符标记为true，直接插入retret += ch;}else{//若字符下标标记为false，需要手动为它匹配if (ch == '('){ret += ch;ret += ')';}else if (ch == ')'){ret += '(';ret += ch;}else if (ch == '['){ret += ch;ret += ']';}else if (ch == ']'){ret += '[';ret += ch;}}}for (auto e : ret){cout << e;}return 0;
}

这道题代码实现时要注意一个细节：

else
{if (stk.empty()){continue;}int top = stk.top();char left = str[top];else if ((ch == ')' && left == '(') ||(ch == ']' && left == '[')){st[i] = st[top] = true;}
}

这里else分支内部嵌套了一组if语句，其中else if应改为if，因为else if是else { if (…) { … }}的简写，必须有一个上层if作为前提，但是如果上层if内部用continue/break跳过了剩余逻辑，那么它的 “同级else if”会因缺少前提if而语法错误。
除此之外，这里不能用else if还有一个原因，else if的语法核心是：必须紧跟在一个if之后，中间不能有任何其他语句。否则会因无法匹配if而报错，而这段代码if和else if之间还有其他语句。

以上就是小编分享的全部内容了，如果觉得不错还请留下免费的关注和收藏
如果有建议欢迎通过评论区或私信留言，感谢您的大力支持。
一键三连好运连连哦~~