当前位置：首页 > news >正文

凸集与优化

news 2025/9/2 9:10:45

什么是凸集

要理解凸集（Convex Set），我们需要从 “凸性” 的核心直觉出发，逐步过渡到数学定义、关键性质和实际应用 —— 它是优化理论、几何、概率统计等领域的基础概念，本质是描述集合中 “任意两点的连线都完全落在集合内” 的特性。

凸组合的定义

凸集的定义依赖 “凸组合（Convex Combination）” 这一概念，我们先明确它，再定义凸集。

基础：凸组合（针对 2 个点）

设两个点 x_1 和 x_2位于 n 维欧几里得空间Rⁿ 中（比如 1 维直线、2 维平面、3 维空间），若存在一个实数λ∈ [0,1]（即 (0≤λ≤1），则点：x= λx_1 + (1-λ)x_2——称为x_1 和 x_2 的凸组合。
直觉解释：当 λ 从 0 变到 1 时，x 从 x_2 连续移动到 x_1，轨迹就是连接 x_1和 x_2 的整条线段。

凸集的严格定义

一个集合 S⊆Rⁿ 是凸集，当且仅当：
对任意两个点x_1∈S,x_2∈S以及任意λ∈[0，1]，它们的凸组合 λx_1+(1-λ)x_2仍属于S
换句话说：集合中任意两点的连线（所有凸组合）都完全包含在集合内。

凸包（多个点的凸组合）

凸集的定义可以推广到 “任意有限个点”：若 S 是凸集，则对 S 中任意 k 个点x_1 ,x_2,…,x_k，以及满足λ_1+λ_2+…+λ_k=1,且λ_i≥0(i=1,…,k)的实数λ_1,…,λ_k它们的凸组合：x=λ_1x_1+λ_2x_2+……+λ_kx_k仍属于 S。
这意味着：凸集中 “任意多个点的加权平均（权重非负且和为 1）” 都不会超出集合

凸集的核心性质

凸集的性质是其在数学和应用中发挥作用的关键，最核心的是 “封闭性”—— 对凸集进行特定操作后，结果仍为凸集：
交集封闭：任意多个凸集的交集仍是凸集
仿射变换封闭：对凸集进行 “线性变换（如缩放、旋转）+ 平移” 后，结果仍是凸集。
凸包（Convex Hull）：任意集合 A⊆ Rⁿ的凸包是 “包含 A 的最小凸集”，本质是 A 中所有点的所有凸组合构成的集合。

什么是凸函数

凸的方向——凸与严格凸

凸函数： 满足定义的基础条件，允许线段上的点与函数图像完全重合（即存在 “平的部分”）。
严格凸函数： 在凸函数的基础上，进一步要求线段严格位于函数图像上方（除端点外无重合），是更强的条件。

凸函数的数学定义

凸函数的定义基于区间内任意两点的线性组合，是理解其本质的核心。我们分 “一元函数” 和 “多元函数”（拓展）两类说明，一元函数是基础

一元凸函数

设函数 f(x)在区间 I（如 [a,b] 或 R上有定义，若对区间内任意两个不同的点 x_1, x_2 ∈ I，以及任意满足0 ≤ λ ≤ 1，都有：f(λx_1+(1−λ)x2)≤λf(x1)+(1−λ)f(x2)，则称 f(x)是区间 I 上的凸函数。

若将不等式改为 严格小于(<)，则 f(x)是严格凸函数
符号解释：

λx_1+(1−λ)x_2：表示 x_1 和 x_2 之间的任意一个点（当 λ=0 时为x_2,λ=1时为x_1,λ=0.5时为中点，记为 x_λ
λf(x_1)+(1−λ)f(x_2):表示函数在 x_1, x_2 处函数值的线性组合，对应平面上连接(x_1, f(x_1))和 (x_2, f(x_2))的线段上，在 (x_λ) 处的纵坐标。

多元凸函数

若函数 f(x)定义在Rⁿ的凸集 D上（凸集：任意两点连线全在集内，如圆盘、长方体），对任意x_1, x_2 ∈ D 和0 ≤ λ ≤ 1，满足：λf(x_1)+(1−λ)f(x_2)≤λx_1+(1−λ)x_2则称 f(x) 是凸集 D 上的凸函数。
(例如二元函数f(x,y) = x²+ y²)

凸优化

凸优化是数学领域的一个小分支，有着比较完善的理论体系和许多有效的求解算法，在生活当中起诸多作用，例如，在机器学习领域：基于损失函数为凸函数，通过凸优化我们可以寻得最优模型参数，令预测结果与真实值之间的误差最小
要理解凸优化中的无约束优化、等式约束优化、不等式约束优化，首先需要明确凸优化的核心前提：目标函数是凸函数，约束集（若存在）是凸集。这一前提保证了问题的局部最优解就是全局最优解，是凸优化区别于非凸优化的关键优势，也是后续三种约束场景的共同基础。

一、凸优化的基础框架

在展开具体约束类型前，先明确凸优化问题的标准形式（含所有约束类型的通用形式）：
在这里插入图片描述
其中：

凸函数： 满足f(λx_1+(1−λ)x_2)≤λx_1+(1−λ)x_2(∀t∈ [0,1] ，x_1,x_2为定义域内点）；
凸集： 集合内任意两点的连线仍在集合内（等式约束的仿射子空间、不等式约束的下水平集均为凸集，其交集也是凸集）。

无约束优化（Unconstrained Optimization）

无约束优化是凸优化中最简单的场景 ——没有任何约束条件，仅需最小化凸目标函数。

1. 问题形式

argmin:x∈Rⁿ f(x)
其中 f: Rⁿ→R是凸函数，定义域通常为全空间 Rⁿ（或其他凸集）

2. 核心性质：最优性条件

对于可微的凸函数 f，全局最优解的充要条件是梯度为零（驻点 = 全局最优）：
∇f(x∗)=0
原因：凸函数的梯度具有 “单调性”——∀x,y，有f(y)≥f(x) + ∇f(x)^T(y-x)。若 ∇f(x^*) = 0,则 f(y) ≥ f(x^*), 对所有 y 成立:
即x^*是全局最优。

3. 经典求解方法

无约束优化的求解核心是 “通过迭代逼近梯度为零的点”，根据是否利用二阶信息（Hessian 矩阵）可分为两类：

方法类别	代表算法	核心思想	适用场景
一阶方法（仅用梯度）	梯度下降（GD）	沿负梯度方向迭代（步长固定或自适应），逐步降低函数值	高维问题（如机器学习中的神经网络）
	动量法（Momentum）	引入“动量”加速收敛（缓解 GD 的震荡）	高维、非光滑目标函数
	Nesterov 加速梯度（AGD）	引入“前瞻步骤”，比动量法收敛更快（理论收敛速率 (O(1/k²))，GD 为 (O(1/k))）	凸函数的快速收敛需求
二阶方法（用 Hessian）	牛顿法	用 Hessian 矩阵近似函数的二次泰勒展开，一步迭代更精准	低维、Hessian 易计算的问题（如逻辑回归）
	拟牛顿法（BFGS/L-BFGS）	用梯度信息迭代逼近 Hessian 的逆（避免直接计算 Hessian，降低复杂度）	中高维问题（如大规模 SVM）

等式约束优化（Equality-Constrained Optimization）

当目标函数的最小化需要满足若干等式约束时，需通过 “拉格朗日乘数法” 将约束融入目标函数，转化为无约束问题求解。

1. 问题形式

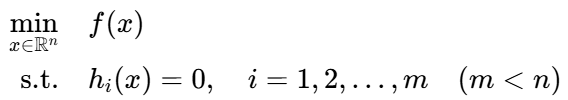
在这里插入图片描述
关键要求：等式约束 (h_i: Rⁿ→R必须是仿射函数（即h_i(x)= a_i^T x + b_i),否则约束集（等式的解）可能非凸，不满足凸优化前提。

2. 核心工具：拉格朗日乘数法

通过引入 “拉格朗日乘子” λ_i ∈ R，将等式约束与目标函数合并为拉格朗日函数：
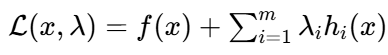
在这里插入图片描述
此时，原等式约束问题的最优性等价于拉格朗日函数的无约束驻点(对 x 和 λ 的偏导均为零)。

3. 最优性条件（KKT 条件简化版）

对于可微的凸目标函数和仿射等式约束，x^* 是全局最优解的充要条件是：存在λ^∗ =(λ_1^∗,…,λ_m^∗ )^T ，满足：
约束可行性： h_i(x^*) = 0（满足等式约束）；
梯度条件：
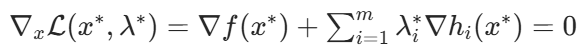
在这里插入图片描述

不等式约束优化（Inequality-Constrained Optimization）

不等式约束是最贴近实际问题的场景（如 “资源不超过上限”“产量非负”），需通过KKT 条件刻画最优性，并借助 “内点法” 等工具求解。

1. 问题形式

在这里插入图片描述
约束集为 “仿射子空间” 与 “凸函数下水平集” 的交集，是凸集。

2. 核心理论：KKT 条件

对于凸优化问题，若满足约束资格（如 Slater 条件：存在严格可行点 x，使得 g_j(x) < 0 且 (h_i(x) = 0)),则 x^*是全局最优解的充要条件是：存在拉格朗日乘子λ^∗ =(λ_1^∗ ,…,λ_m^∗)^T,和 μ^∗ =(μ_1^∗ ,…,μ_p^∗)^T ，满足以下 5 个条件（KKT 条件）：

KKT 条件类别	具体形式	直观含义
1. 原始可行性	h_i(x^) = 0 (∀i) ; g_j(x^) ≤ 0 (∀ j)	最优解必须满足所有约束
2. 对偶可行性	μ_j^* ≥ 0 (∀ j)	不等式约束的乘子非负（凸函数的梯度惩罚方向需合理）
3. 互补松弛	μ_j^* g_j(x^*) = 0 (∀ j)	若约束 g_j(x^) < 0 （非活性约束），则 μ^ = 0 ；若μ_j^* > 0 ，则 g_j(x^*) = 0 （活性约束）
4. 梯度条件		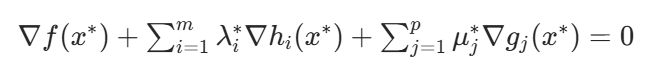拉格朗日函数对 x 的梯度为零（驻点条件）
5. 约束资格 (Slater)	存在 x 使得 g_j(x) < 0 (∀ j) 且 h_i(x) =0 (∀ j)	保证 KKT 条件的充分性（避免 “伪最优解”）

3. 经典求解方法

不等式约束的核心是 “处理不等式约束的活性 / 非活性状态”，常用方法包括：
（1）内点法（Interior-Point Method）
核心思想：通过 “障碍函数”（如对数障碍函数将不等式约束融入目标函数，构造 “障碍问题”：
在这里插入图片描述
其中 t > 0 是 “障碍参数”，t 越小，障碍问题的解越接近原问题的最优解。
适合大规模问题（如线性规划、二次规划），是主流凸优化软件（CVX、Gurobi）的核心算法。

（2）增广拉格朗日法（Augmented Lagrangian Method）

核心思想：在拉格朗日函数中加入 “二次惩罚项”，平衡约束满足度与目标函数最小化：
在这里插入图片描述
其中 ρ > 0是惩罚参数，通过迭代调整 ρ、λ、μ，逐步逼近最优解。

常见的近似优化

SGD（Stochastic Gradient Descent，随机梯度下降）

SGD 是最基础的近似优化算法，是批量梯度下降（BGD）的随机版本。

核心思想

在传统的批量梯度下降中，每次迭代需要计算所有样本的梯度（计算成本高，尤其数据量大时）：
在这里插入图片描述
（(f_i(x) 是第 i 个样本的损失函数，N 是总样本数，eta 是学习率）
SGD 的改进：每次迭代仅随机选择 1 个样本（或一小批样本，称为小批量 SGD，Mini-batch SGD）计算梯度，用局部梯度近似全局梯度：

改进：小批量 SGD（Mini-batch SGD）

实际中常用 “小批量”（如 32、64、128 个样本）替代单个样本，平衡效率与稳定性：
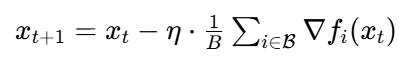
在这里插入图片描述
（beta是随机选取的小批量样本，B 是批量大小）

Adagrad（Adaptive Gradient，自适应梯度）

Adagrad 针对 SGD 的 “固定学习率” 问题，为每个参数分配自适应的学习率，适合处理稀疏数据（如自然语言、推荐系统）。

核心思想

对每个参数 x_j，累计其历史梯度的平方和：
在这里插入图片描述
学习率随历史梯度平方和的平方根衰减（梯度大的参数，学习率衰减更快）：

Adam（Adaptive Moment Estimation，自适应动量估计）

Adam 结合了动量法（Momentum） 和RM Sprop（Adagrad 的改进）的优点，是目前深度学习中最常用的优化算法之一。

核心思想

Adam 维护两个状态变量：
一阶动量 m_t： 梯度的指数移动平均（类似动量法，平滑梯度方向）；
二阶动量 v_t： 梯度平方的指数移动平均（类似 RMSprop，自适应学习率）。
具体更新公式：
在这里插入图片描述

算法对比

算法	核心特点	收敛速度	稳定性	适用场景	典型超参数
SGD	随机梯度，固定学习率	慢	差	小规模数据，简单模型	学习率 eta，批量大小 B
Adagrad	累计梯度平方，自适应学习率衰减	中	中	稀疏数据（如文本、推荐）	初始学习率 eta
Adam	动量 + 自适应二阶动量，偏差修正	快	好	深度学习、大规模数据、非凸问题	(eta = 0.001, beta_1 = 0.9, beta_2 = 0.999)