当前位置：首页 > news >正文

C语言：树的实现和剖析

news 2025/9/2 8:28:07

一、引言

二、树的基本概念

2.1、树的定义

2.2、树的相关术语

2.3、树的表示法

三、二叉树

3.1、二叉树的概念和结构

3.2、特殊的二叉树

3.2.1、满二叉树

3.2.2、完全二叉树

3.3、二叉树的存储

3.3.1、顺序结构

3.3.2、链式结构

四、实现顺序结构的二叉树

4.1、堆的概念与结构

4.2、堆的实现

4.2.1、定义堆的结构

4.2.2、堆的初始化

4.2.3、入堆

4.2.4、向上调整

4.2.5、判断堆是否为空

4.2.6、删除堆顶

4.2.7、向下调整

4.2.8、取堆顶

4.2.9、销毁

4.3、堆排序

4.3.1、核心思想

4.3.2、具体实现

4.3.3、真正的堆排序

五、实现链式结构的二叉树

5.1、节点定义

5.2、二叉树的遍历

5.2.1、前序遍历

5.2.2、中序遍历

5.2.3、后序遍历

5.2.4、层次遍历

5.3、求二叉树的结点个数

5.4、求二叉树叶子结点的个数

5.5、求二叉树第 k 层的结点个数

5.6、求二叉树的深度

5.7、查找二叉树特定值的结点

5.8、二叉树的销毁

六、练习题

6.1、单值二叉树

6.2、检查两颗二叉树是否相同

6.3、对称二叉树

6.4、另一棵树的子树

6.5、二叉树的遍历

6.6、根据两种已知遍历，求树的结构

七、结语

一、引言

在学习完顺序表，链表，栈和队列之后，我们就要学习树这个新的结构，前面学的都是线性表，而树不是线性表，是一种非线性结构。树的应用很广泛，最常见的就是我们电脑中的文件夹系统，其结构就是一个树。

本文将带你认识了解树的奥秘，let' go

二、树的基本概念

2.1、树的定义

树是一种非线性结构，它是由 n (n>=0)个有限节点组成的一个具有层次关系的集合。

2.2、树的相关术语

（1）父节点/双亲节点：若一个节点有子节点，则该节点是其子节点的父节点/双亲节点；

（2）子节点/孩子节点：一个节点指向的下一层节点；

（3）子孙：以某结点为根的⼦树中任⼀结点都称为该结点的⼦孙；

（4）路径：⼀条从树中任意节点出发，沿⽗节点-⼦节点连接，达到任意节点的序列；

（5）节点的度：一个节点有几个孩子节点，它的度就为几；

（6）树的度：一棵树中，最大的结点的度成为树的度；

（7）叶子节点/终端节点：度为0的节点，也就是没有孩子的节点；

（8）分支节点/非终端节点：度不为0的节点；

（9）兄弟节点：具有相同父节点的节点互相成为兄弟节点；

（10）节点的层次：从根开始定义，根为第一层，根的子节点为第二层，依次类推；

（11）树的高度/深度：树中节点的最大层次；

（12）节点的祖先：从根节点到该节点所经分支上的所有节点；

（13）森林：由 m (m>0)个互不相交的树的集合。

2.3、树的表示法

孩子兄弟表示法：

struct TreeNode
{struct TreeNode* child;     //从左边开始的第一个孩子节点struct TreeNode* bother;    //指向其右边的下一个兄弟节点int data;   //数据域
};

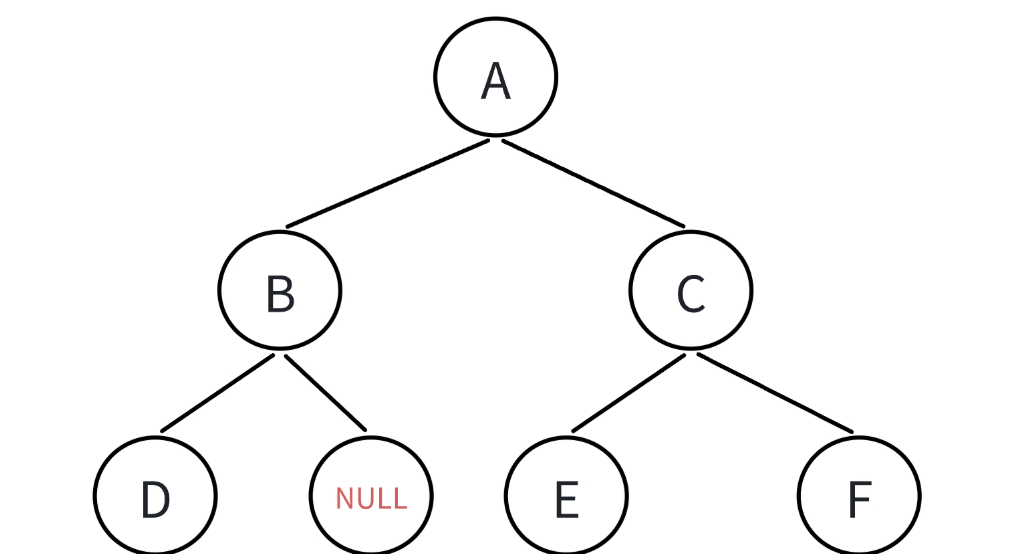
例如，这棵树的孩子兄弟表示法为：

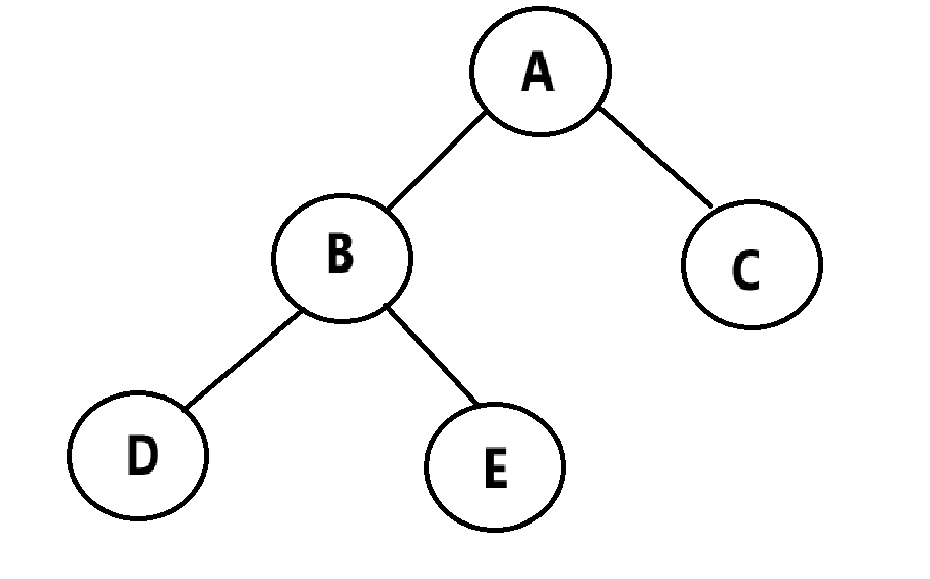
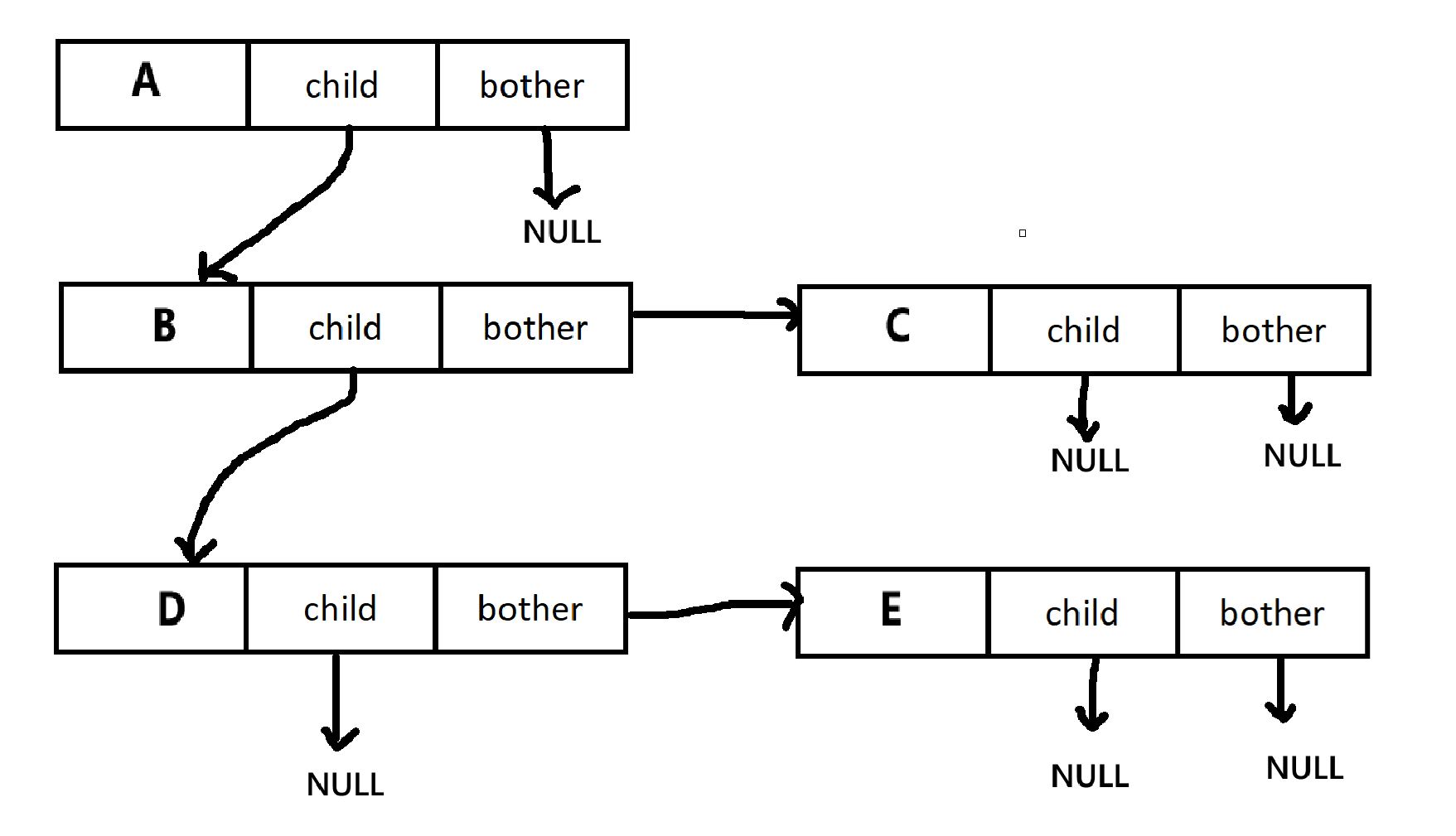
当然还有其他表示法，例如左右孩子法等，后面会专门介绍。

三、二叉树

3.1、二叉树的概念和结构

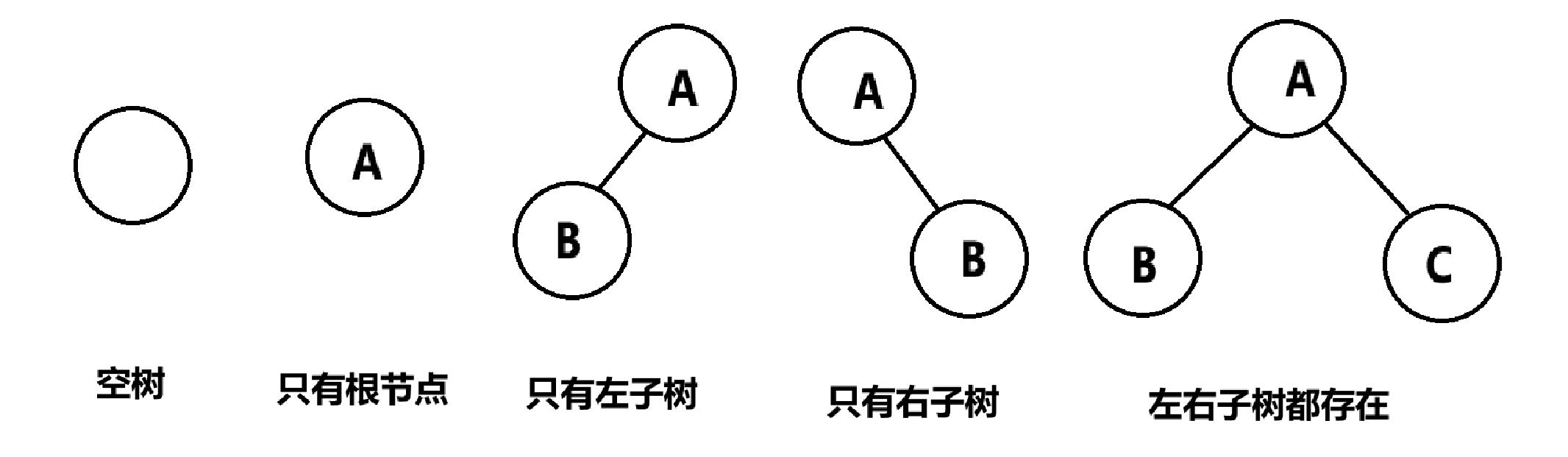
一颗二叉树是节点的一个有限集合，该集合由一个根节点加上两颗分别为左子树和右子树的二叉树组成或者为空。通俗一点，就是，每个节点最多由两个孩子。

特点：

（1）二叉树不存在度大于2的结点；

（2）二叉树的子树有左右之分，次序不能颠倒，因此二叉树也是有序树；

（3）对于任意的二叉树，都是由以下几种情况复合而成：

3.2、特殊的二叉树

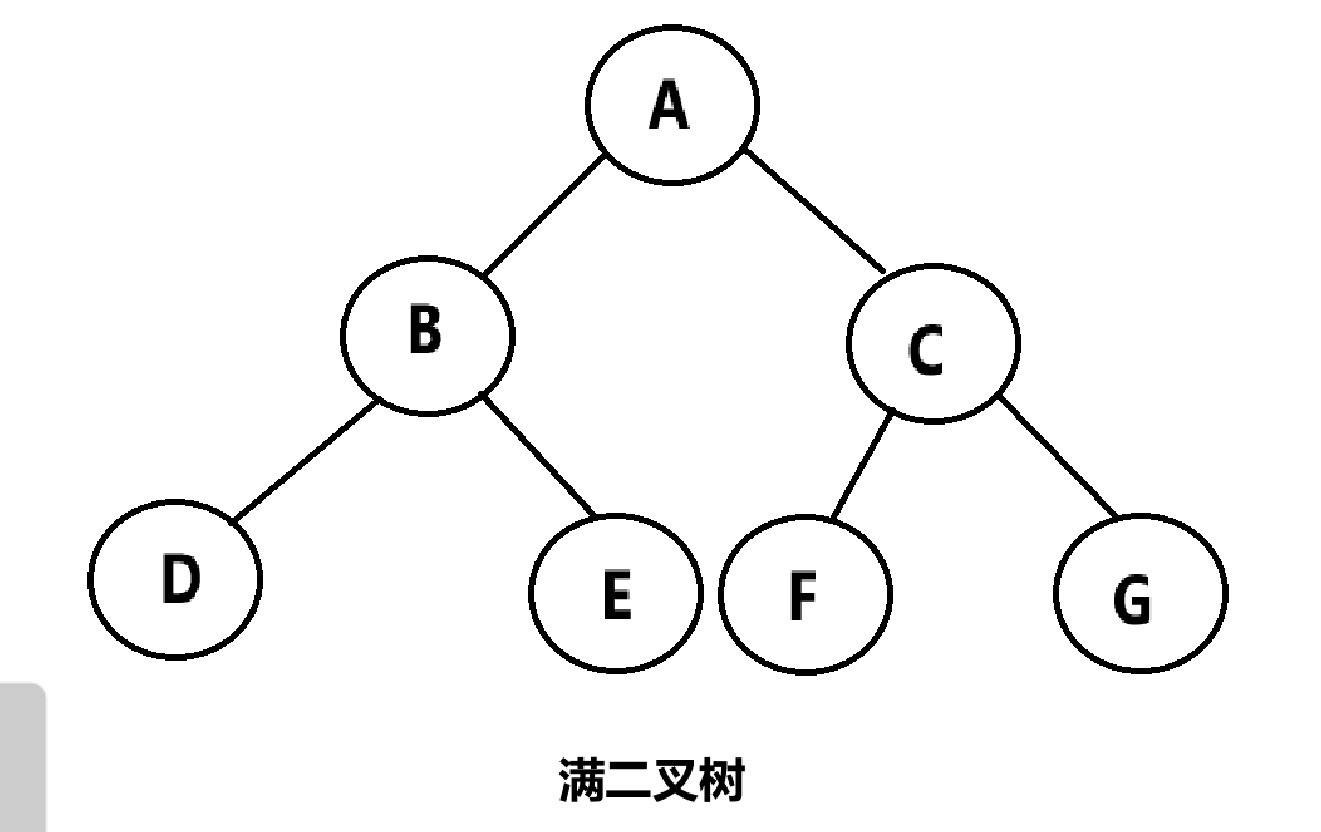
3.2.1、满二叉树

每一层的节点数都达到最大值，也就是说，如果一个满二叉树的层次为 k ，则，它的第 k 层有 2^(k-1) 个节点，节点总数为 2^k -1个。说人话就是，一颗二叉树，除了叶子结点的其余节点，都有两个孩子。

3.2.2、完全二叉树

对于深度为 k ，有 n 个节点的二叉树，当且仅当其每个节点都与深度为 k 的满二叉树中编号从1到n的结点一一对应时，称之为完全二叉树。说人话就是，去掉完全二叉树的最后一层，剩下的就是满二叉树，而这个完全二叉树的最后一层的结点必须从左到右依次摆放。

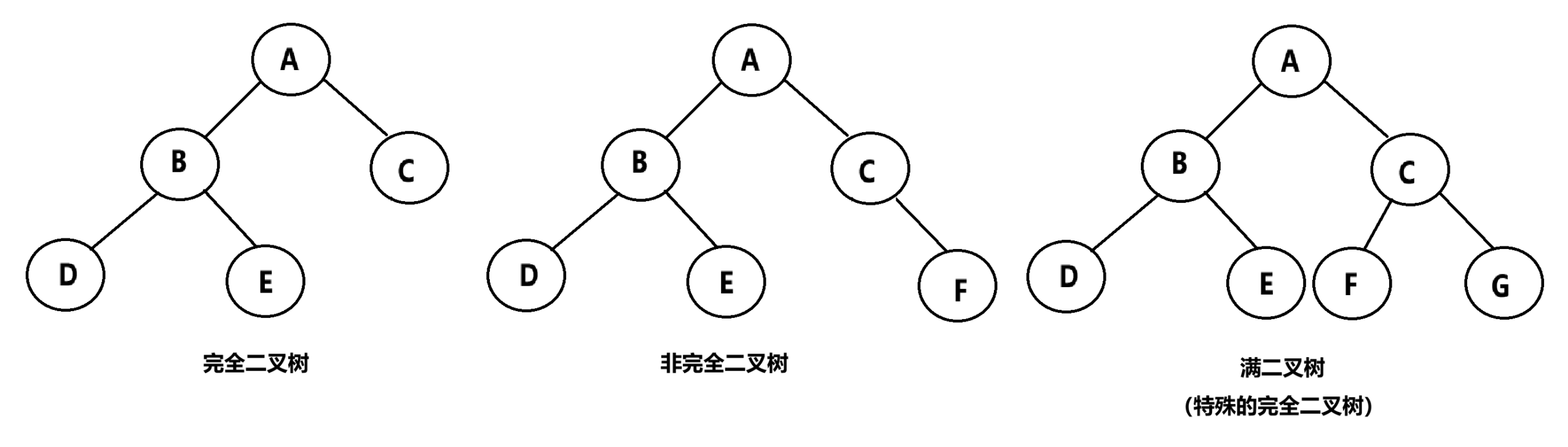
注意哦，满二叉树也符合完全二叉树的要求，因此，满二叉树也是一种完全二叉树。

性质：具有 n 个节点的满二叉树的深度为 $h = \log _{2}(n+1)$

3.3、二叉树的存储

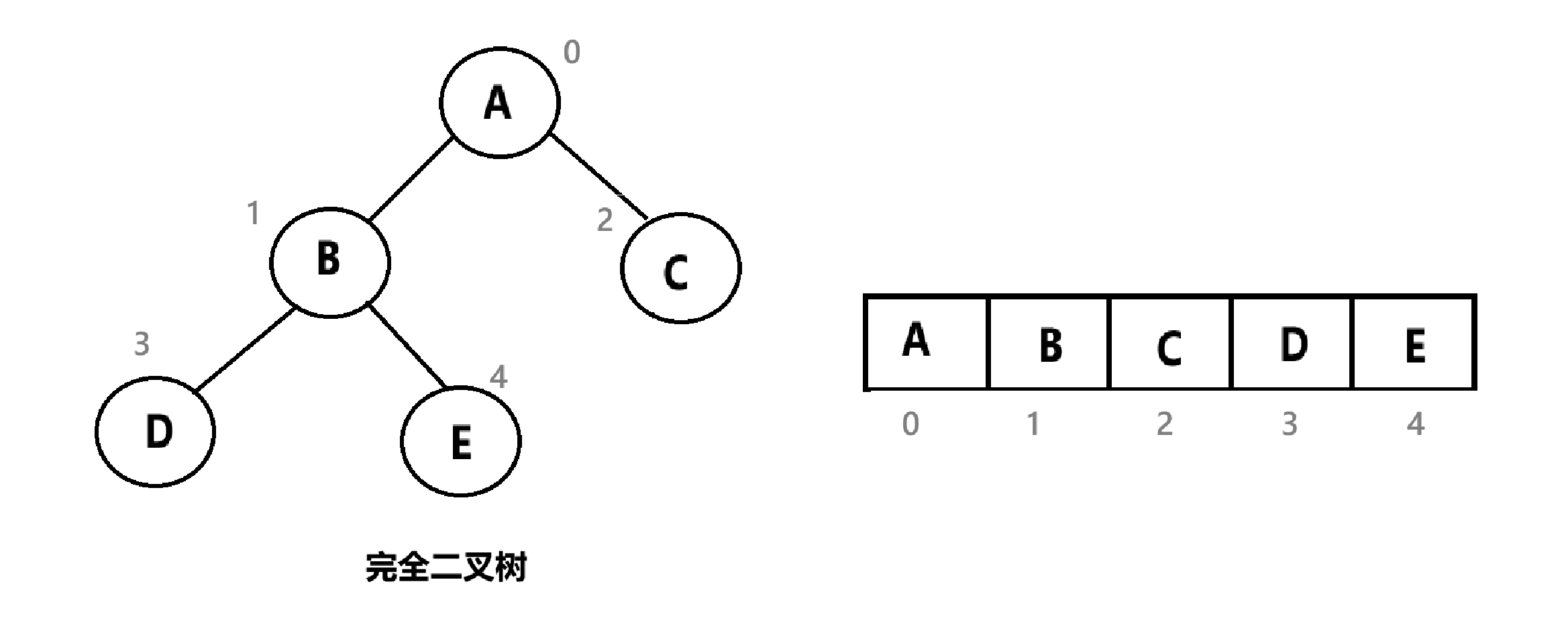
3.3.1、顺序结构

使用数组存储，一般只适用表示完全二叉树（堆）

如图：

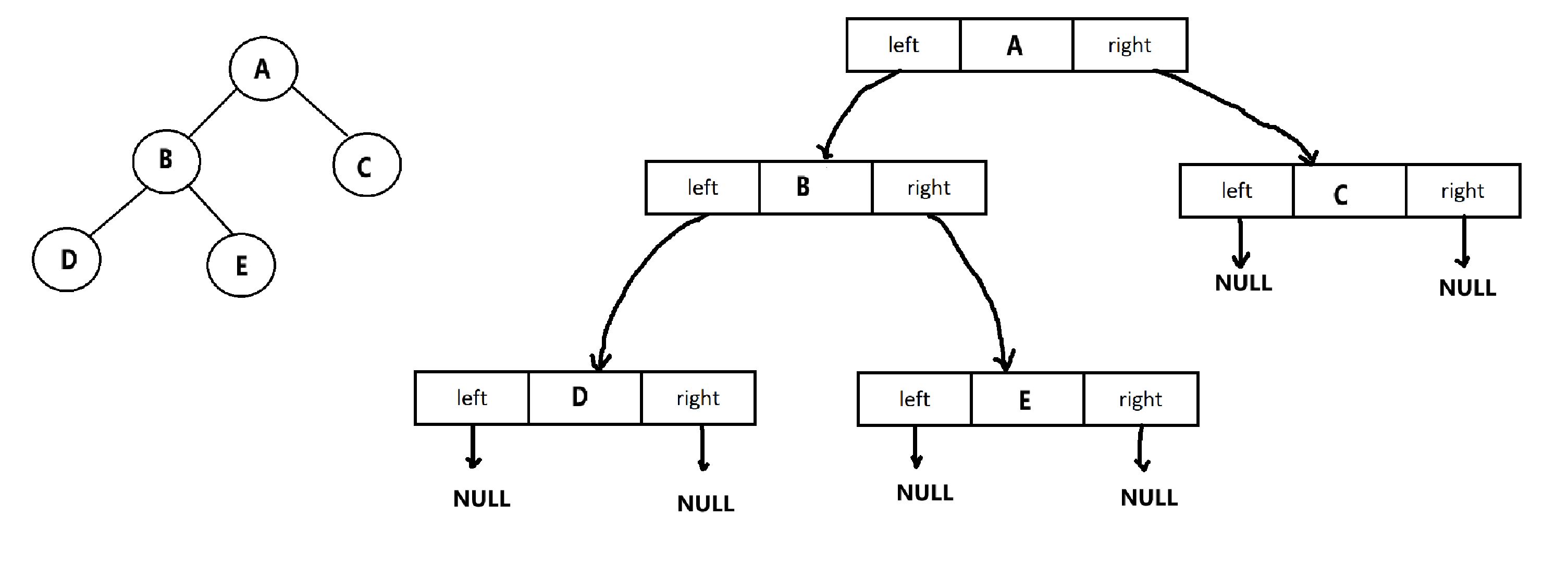
3.3.2、链式结构

用链表表示一颗二叉树

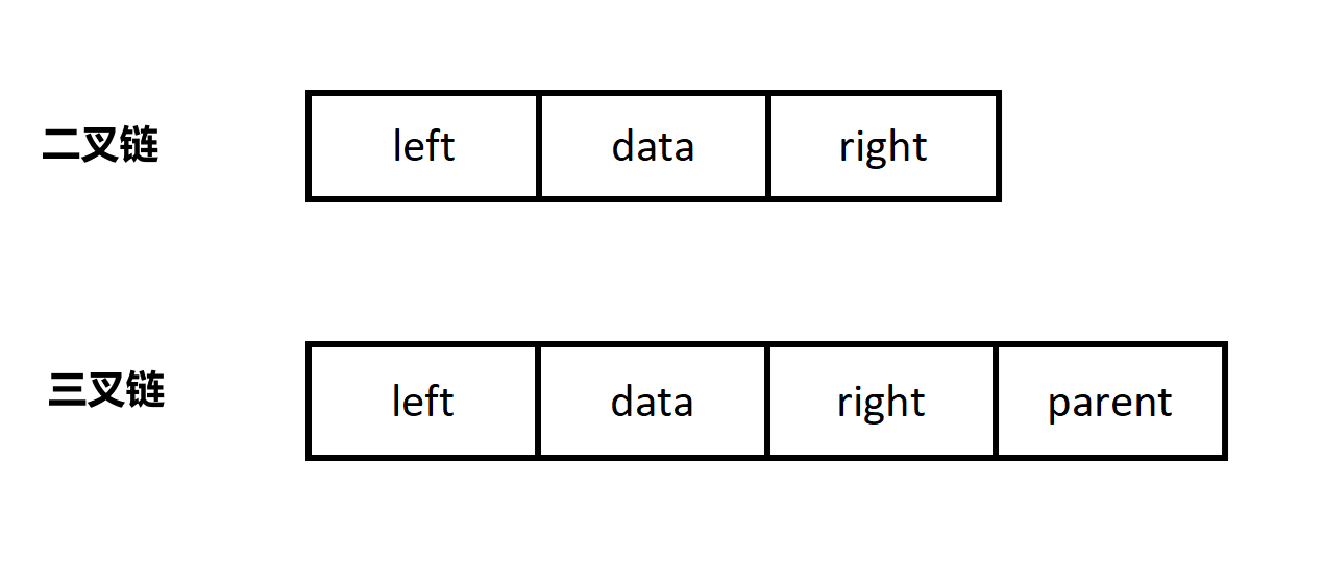
如图，用链表表示树可以使用二叉链，也可以使用三叉链，三叉链比二叉链多了一个指向父节点的指针而已，后面使用红黑树会用到，本章还是使用较为简单的二叉链

四、实现顺序结构的二叉树

使用顺序结构的二叉树一般都是堆，堆是一种完全二叉树

4.1、堆的概念与结构

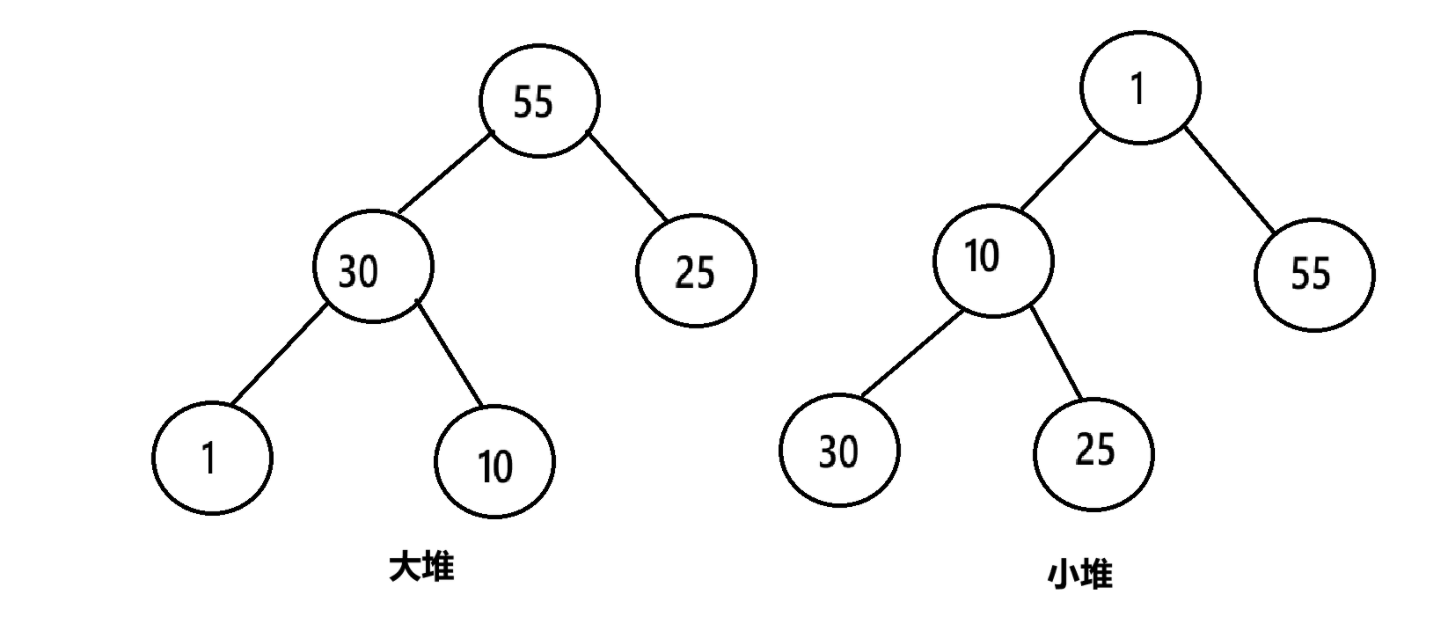
如果有一个关键码的集合 k = { k0, k1, k2, …… ， kn-1}，把它所有圆的按完全二叉树的顺序存储方式存储在一个堆数组中，并满足： ki <= k2i+1，则称为小堆。说人话，就是如果一棵完全二叉树的所有节点都满足：孩子节点比父节点大（小），则称该二叉树为小堆（大堆）

性质：

（1）堆中某个节点的值总是不大于或不小于其父节点的值；

（2）堆总是一棵完全二叉树；

（3）堆顶是最值；

注意：对于序号为 i 的节点，有以下特性：

（1）若 i > 0 ，i 的父节点的序号为 (i-1)/2（向下取整）；

若 i = 0 ，说明该节点为根节点，没有父节点；

（2）若 2i+1 < n, 则该节点的左孩子序号为 2i+1;

若 2i +1 >= n, 则没有左孩子；

（3）若 2i+2 < n, 则该节点的右孩子序号为 2i+2;

若 2i+2 >= n ，则该节点没有右孩子。

4.2、堆的实现

堆用数组实现。

4.2.1、定义堆的结构

由于数组的物理结构与顺序表非常近似，所以堆可以认为是用顺序表实现的，因此，堆的实现和顺序表非常近似。

typedef int HeapDataType;
typedef struct Heap
{HeapDataType* arr;   //数组int size;     //有效元素个数int capacity;   //容量
}Heap;

4.2.2、堆的初始化

这里我们必须传回堆的地址，因为我们要对堆里面的内容做出改变！里面的指针置为NULL，size和capacity都置为0.

void HeapInit(Heap* hp)
{assert(hp);hp->arr = NULL;hp->size = hp->capacity = 0;
}

4.2.3、入堆

和顺序表一样，要先判断是否需要扩容，然后在进行入堆

void HeapPush(Heap* hp, HeapDataType x)
{assert(hp);//判断是否需要扩容if (hp->size == hp->capacity){int newCapacity = hp->capacity == 0 ? 4 : 2 * hp->capacity;HeapDataType* tmd = (HeapDataType*)realloc(hp->arr, sizeof(HeapDataType) * newCapacity);if (tmd == NULL){perror("malloc fail!");exit(1);}hp->arr = tmd;hp->capacity = newCapacity;}//入堆hp->arr[hp->size++] = x;AdjustUp(hp->arr , size-1);
}

注意，每次入堆后需要进行向上调整，以保证堆的正确性，具体见4.2.4

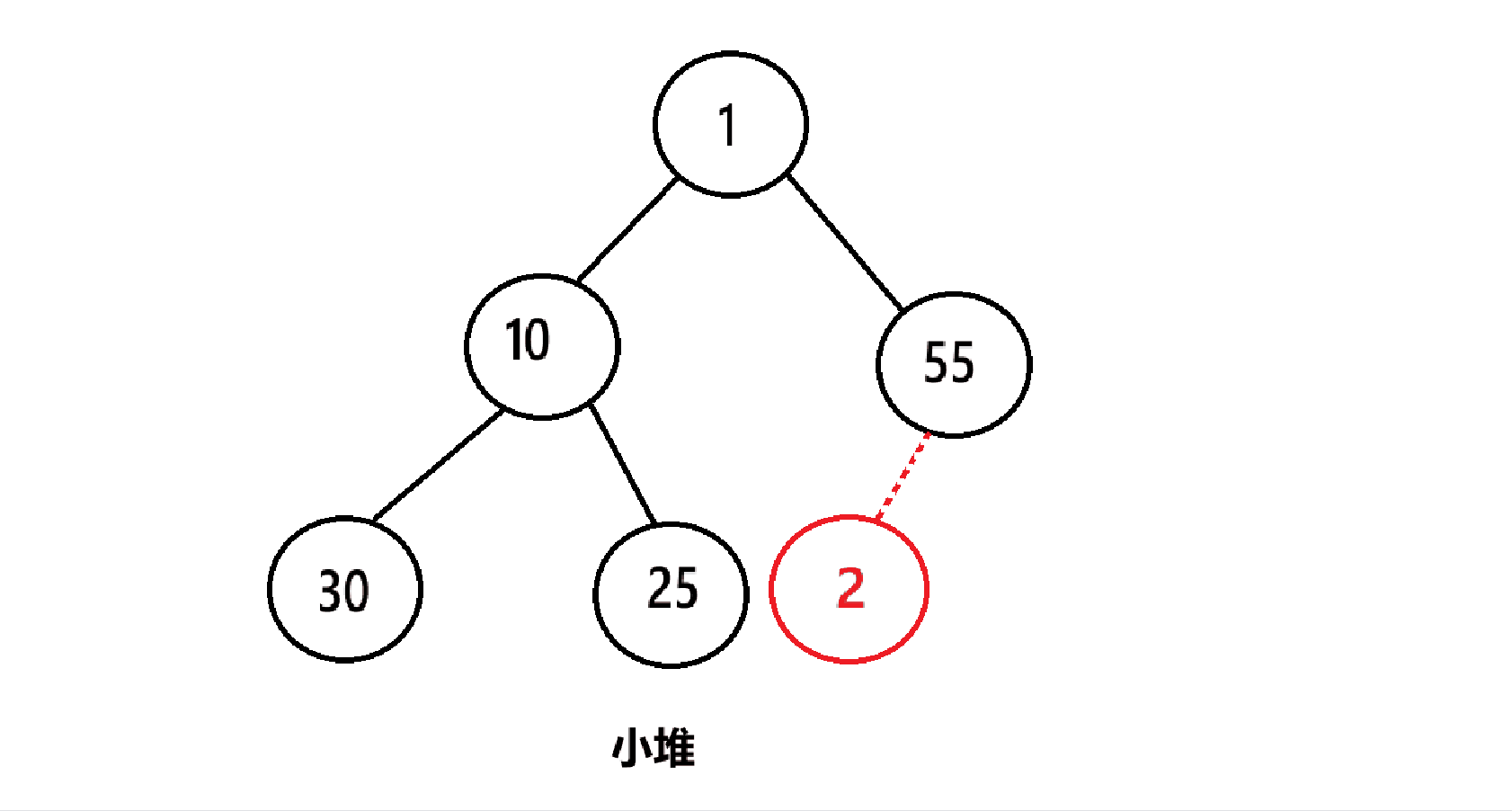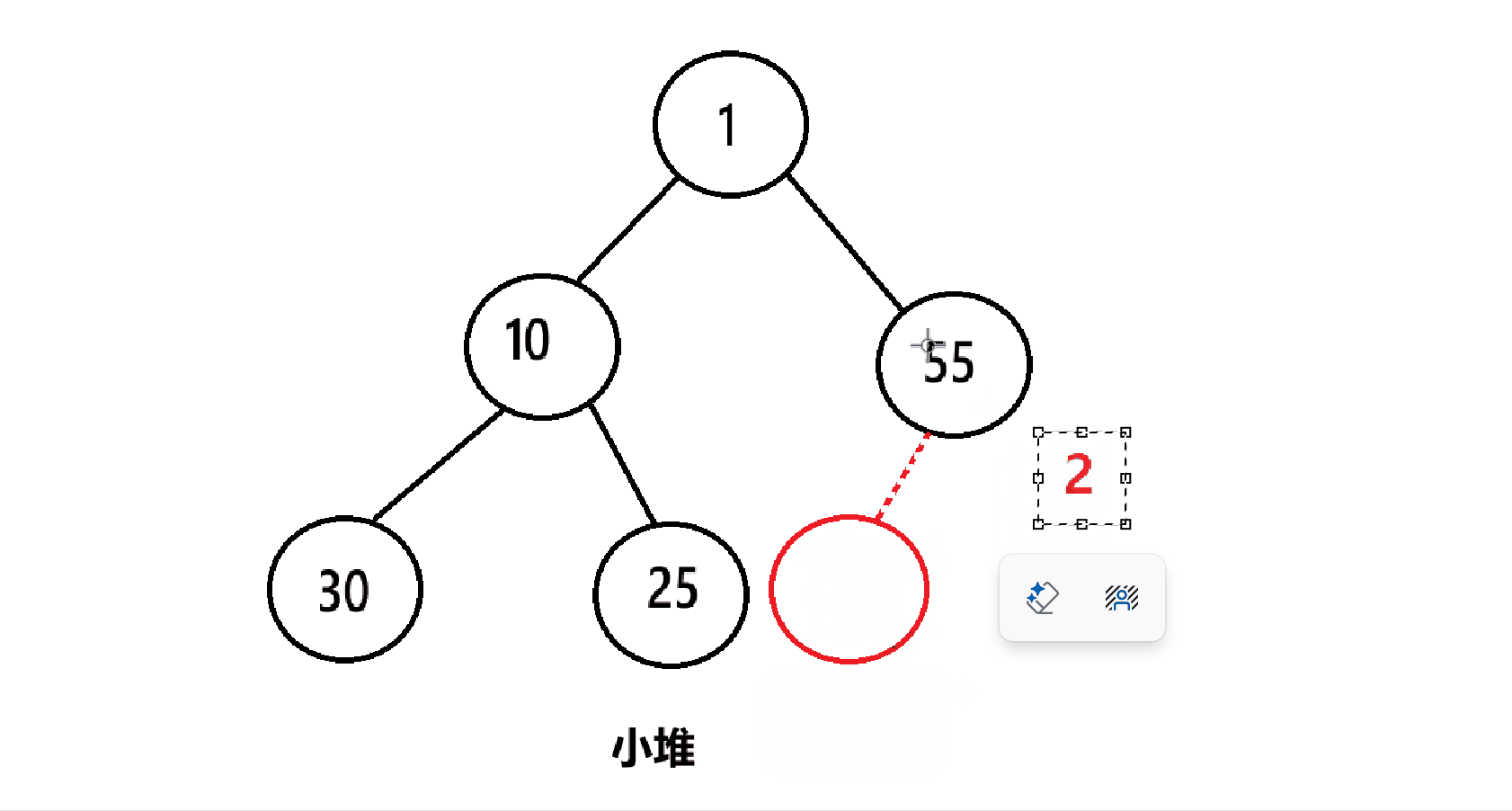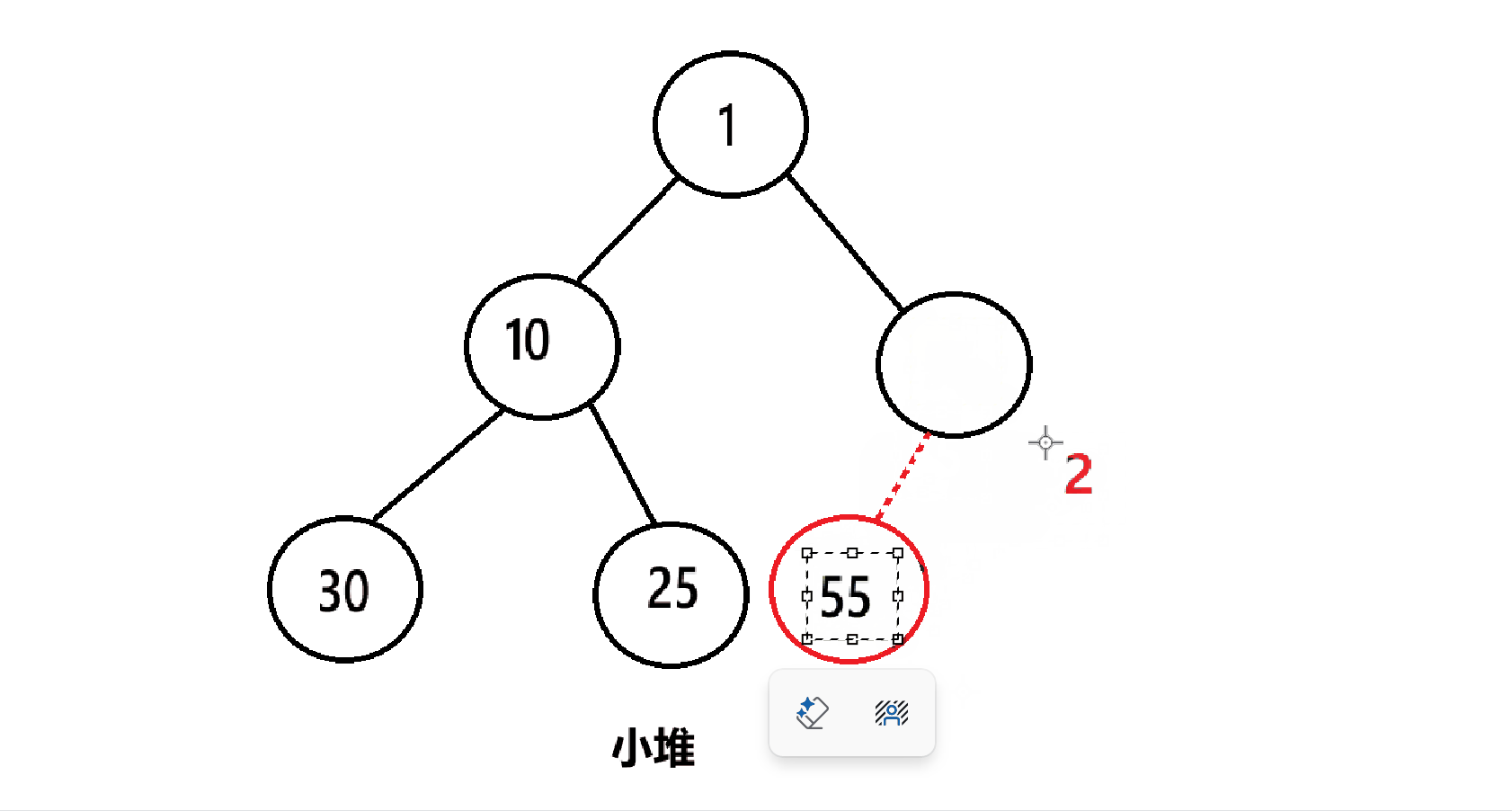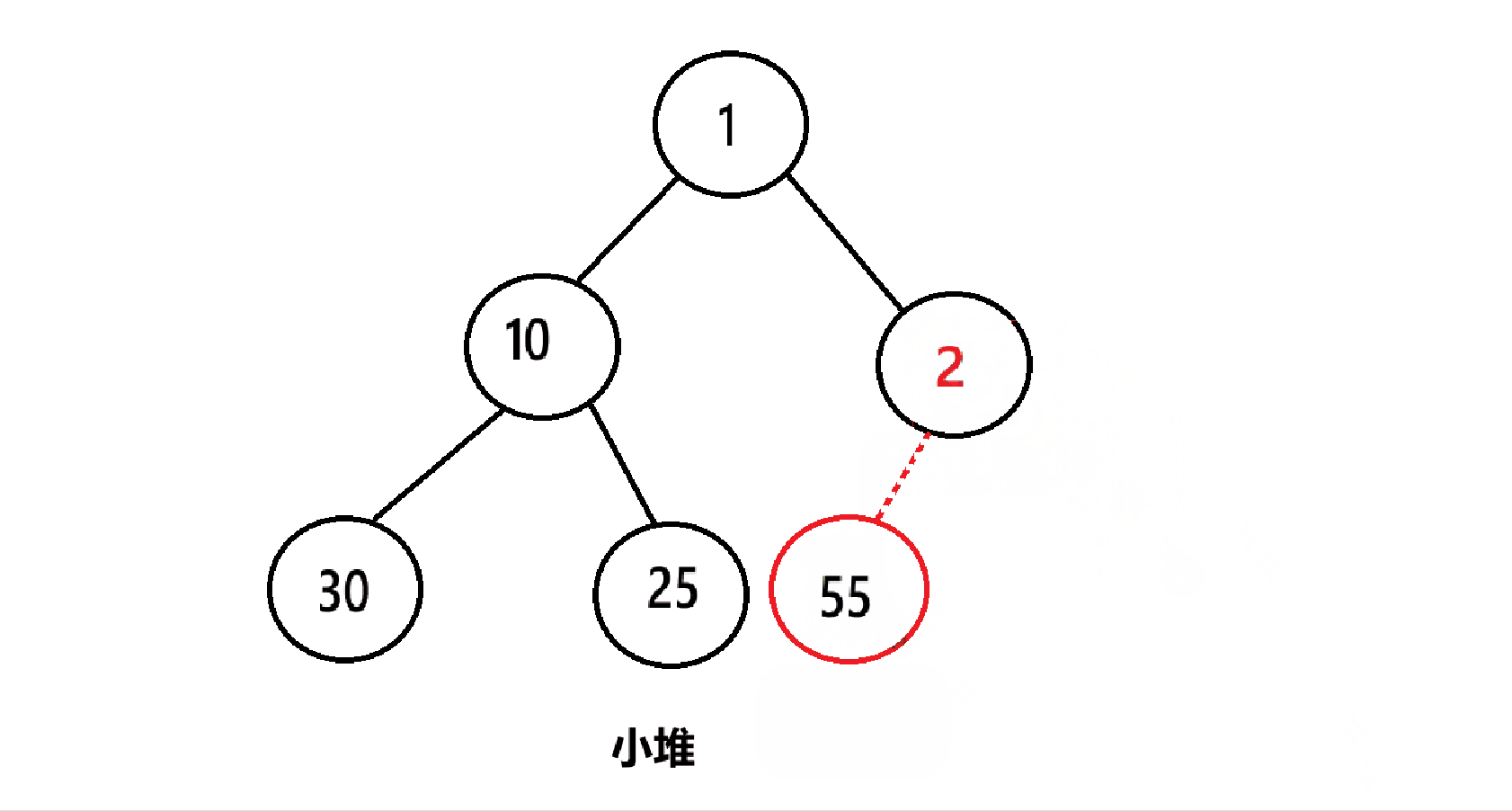
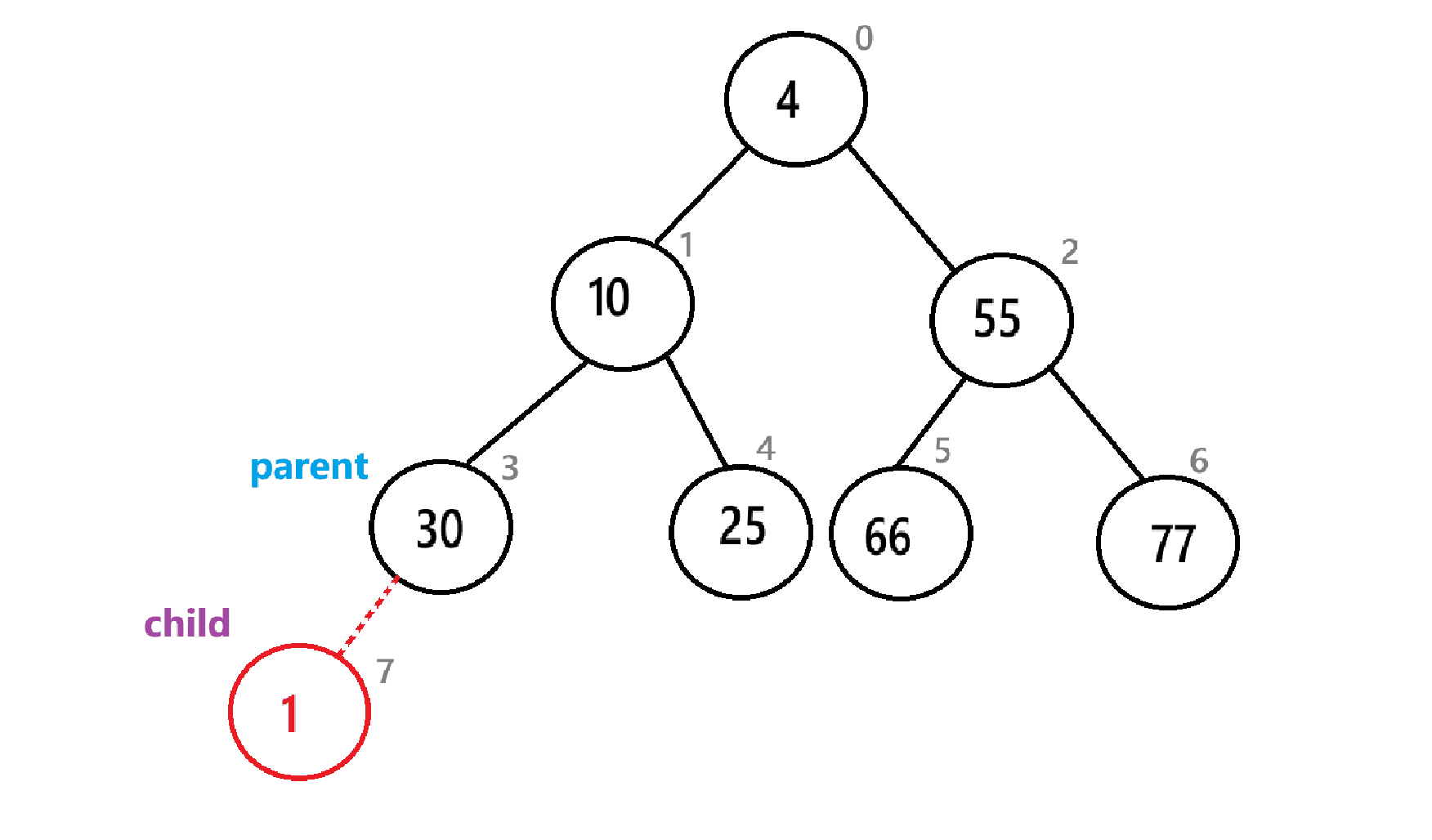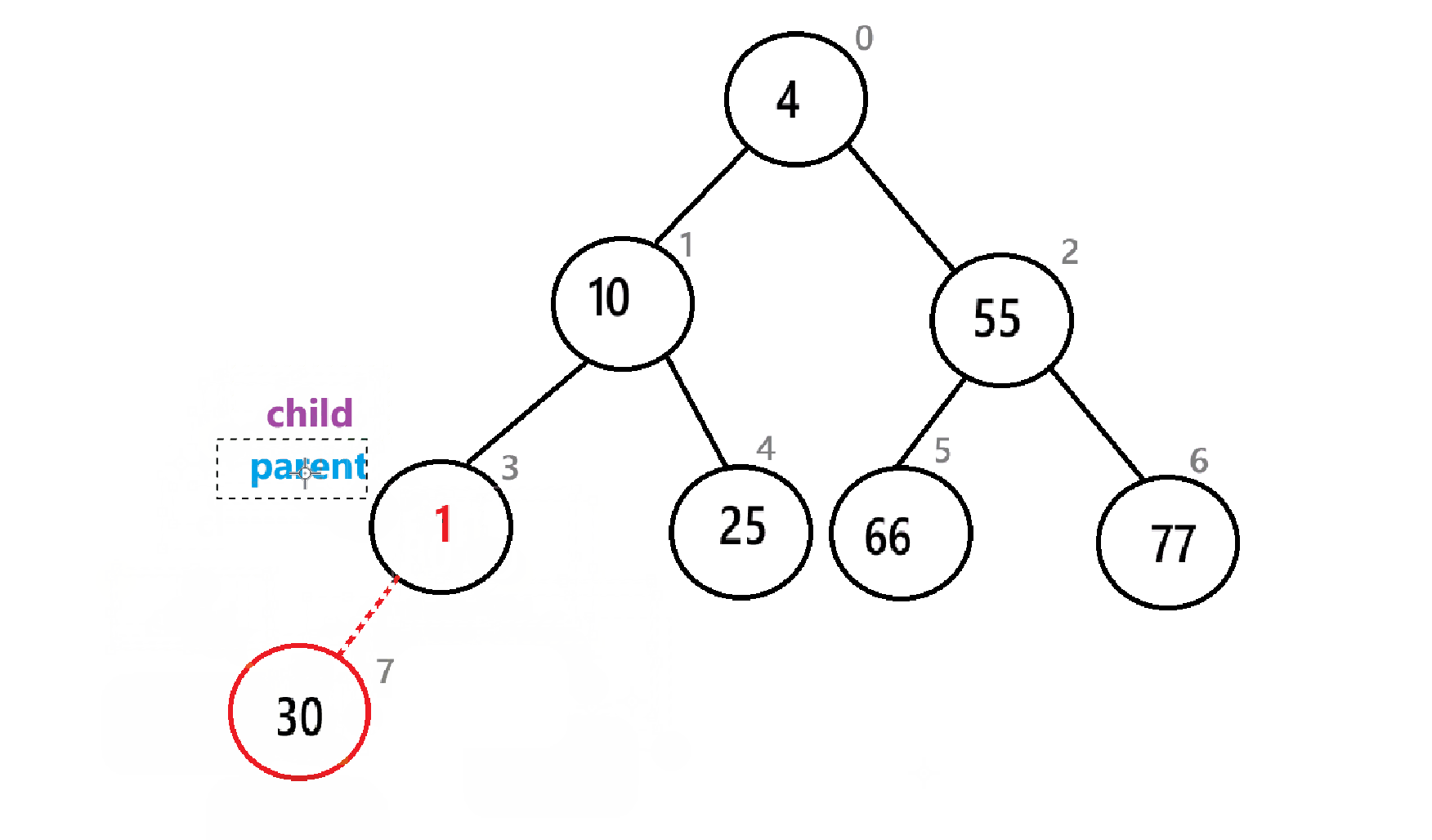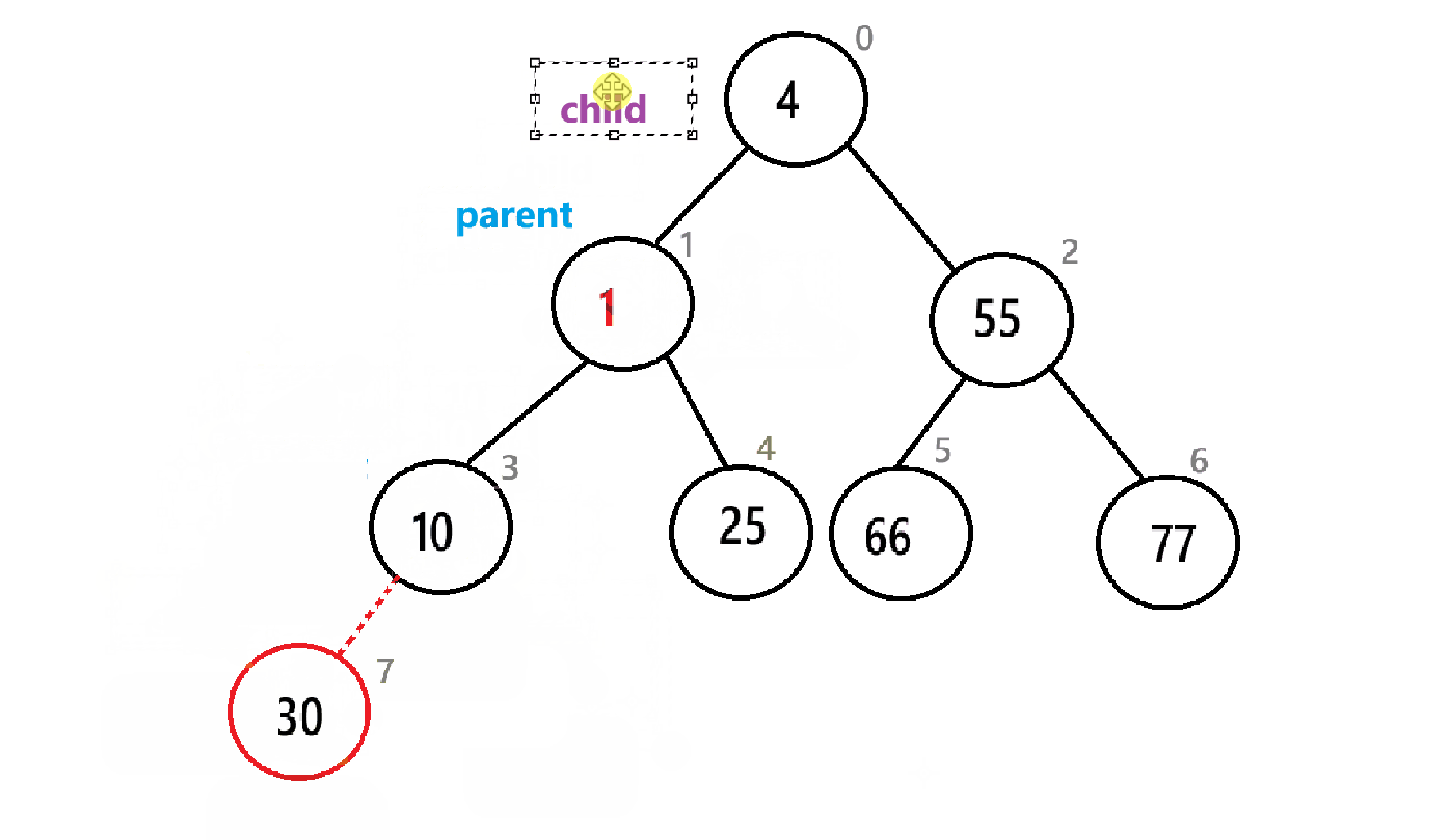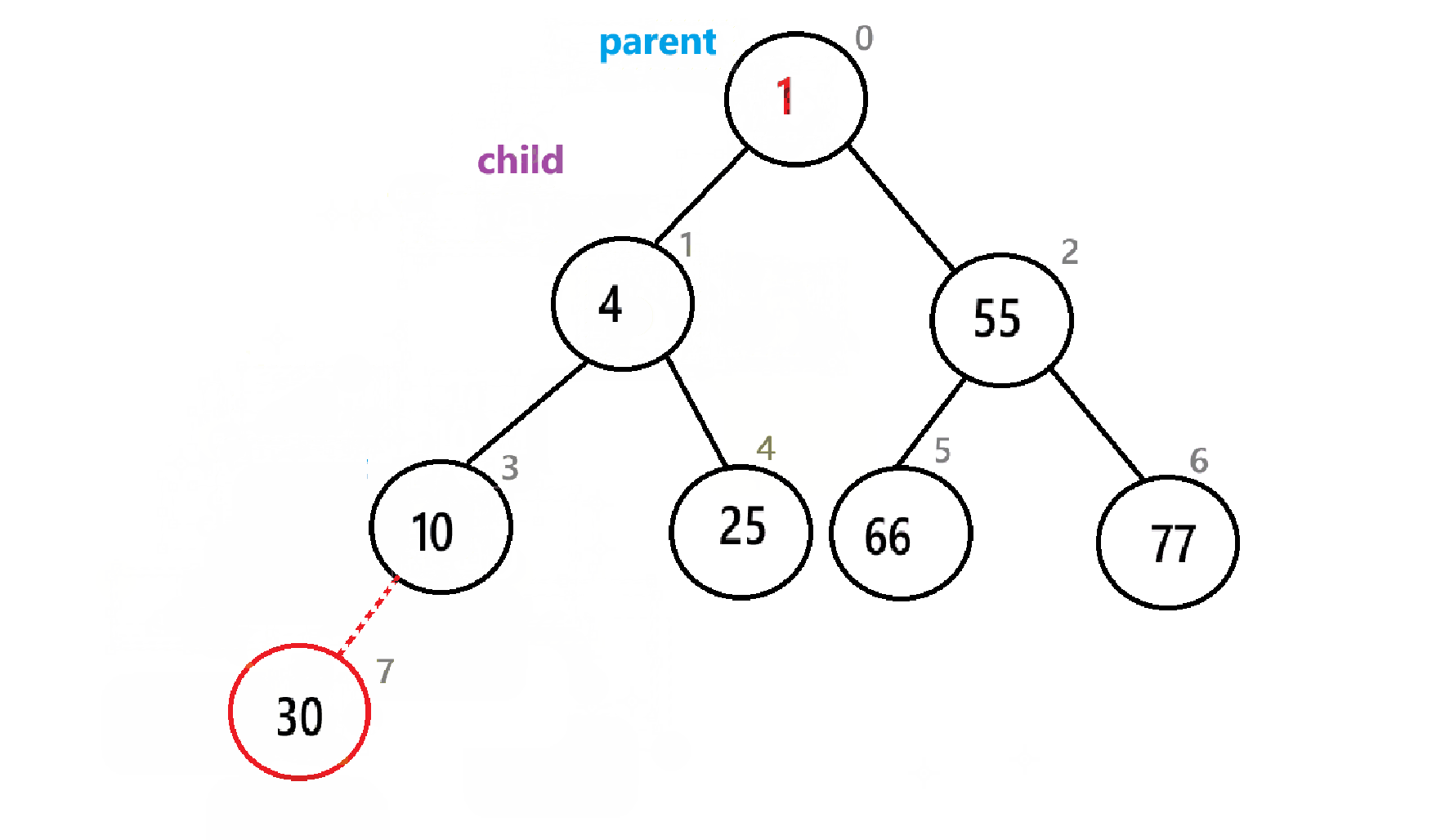
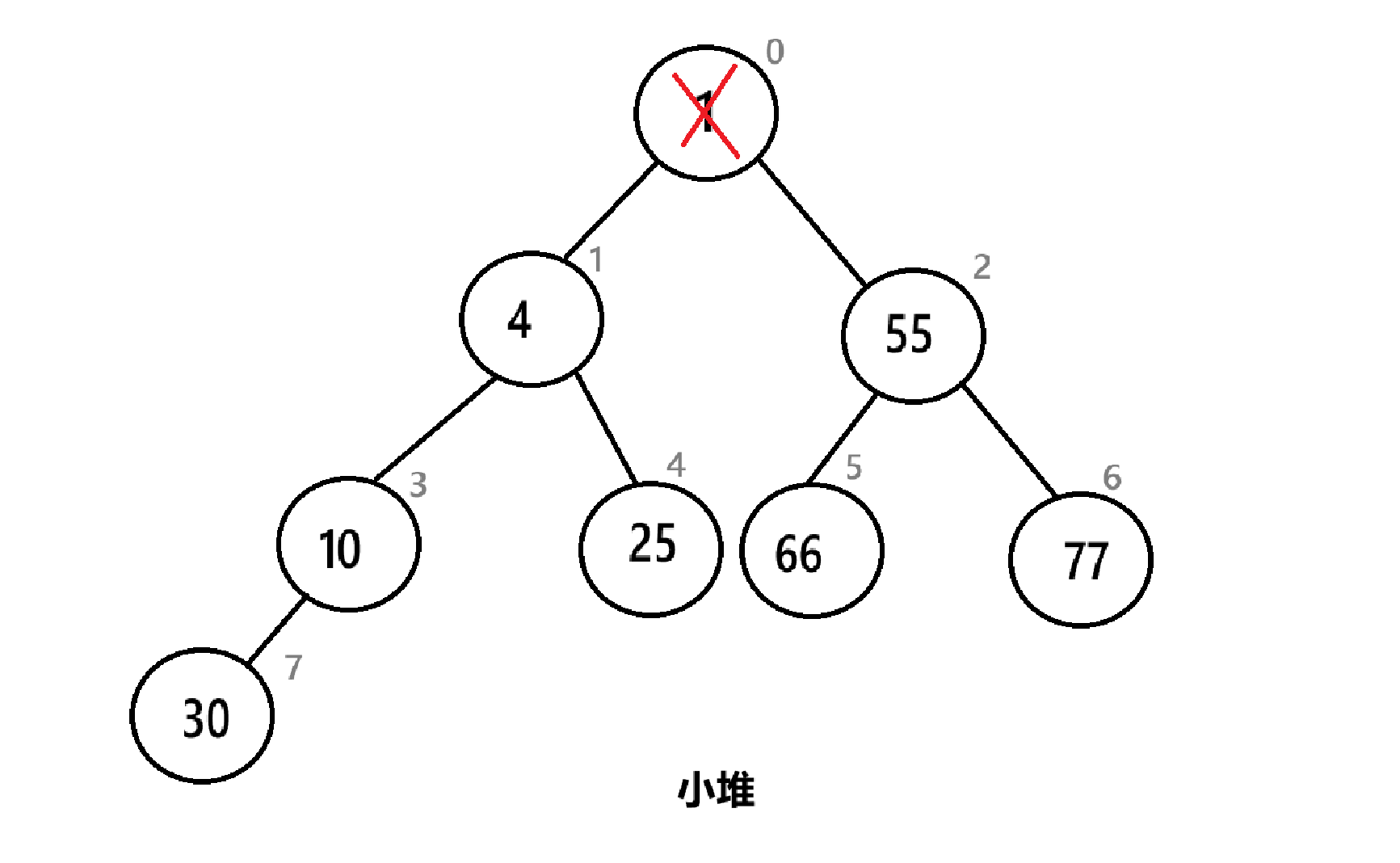
4.2.4、向上调整

在每次入堆后，我们需要向上调整，以此使得数组中的元素满足堆的条件

例如，在这个小堆里插入一个2：

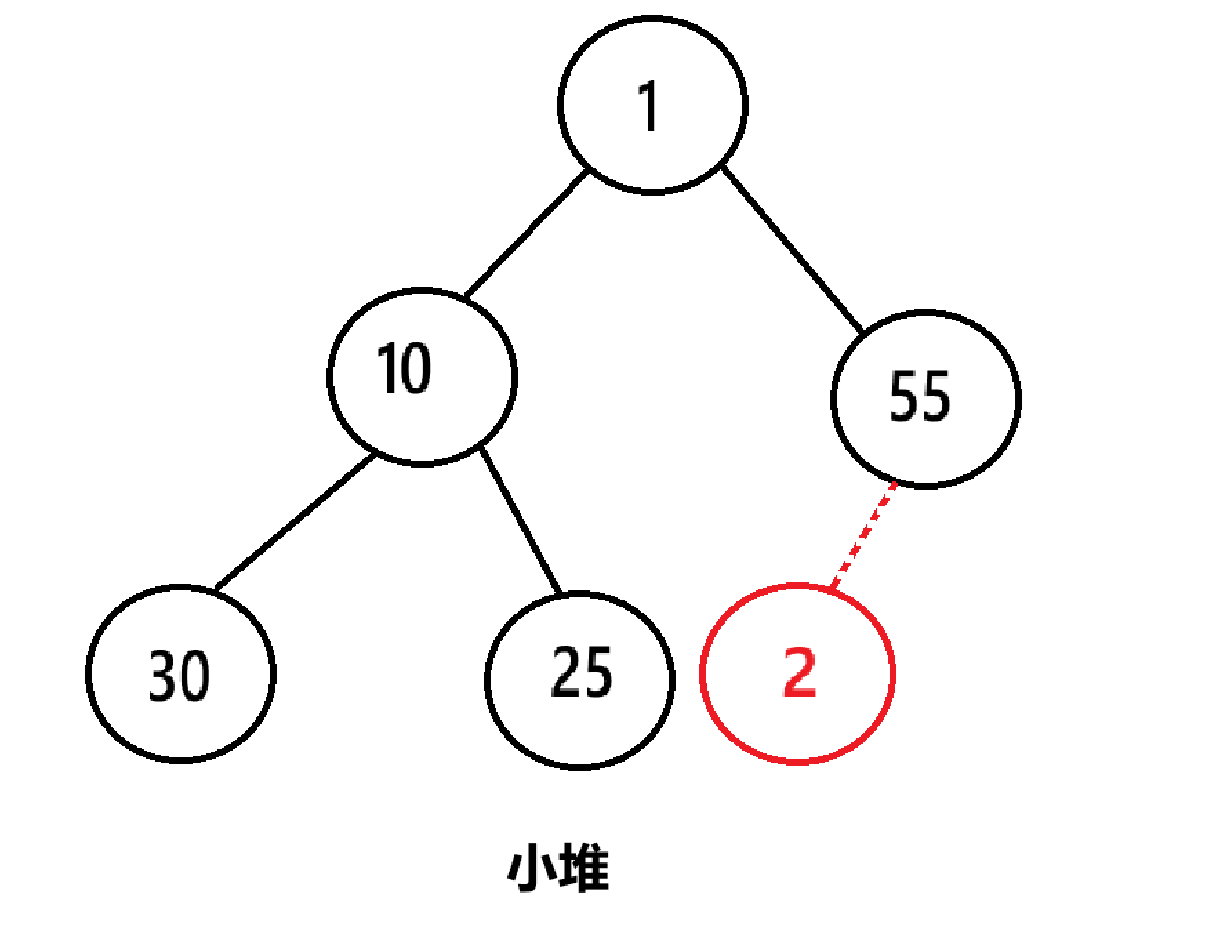
插入2后要进行向上调整：

上动图只是一个简单的过程，实际情况要比这个复杂，下面是具体算法步骤：

具体代码如下：

void AdjustUp(HeapDataType* arr, int child)
{assert(arr);int parent = (child - 1) / 2;while (parent >= 0){if (arr[parent] > arr[child]){Swap(&arr[parent], & arr[child]);child = parent;parent = (child - 1) / 2;}else{break;}}
}

4.2.5、判断堆是否为空

bool HeapEmpty(Heap* hp)
{assert(hp);return hp->size == 0;
}

4.2.6、删除堆顶

如图，直接删去堆顶：

剩下的元素明显违背了堆的原则，所以需要进行一些操作。

先将堆顶和末尾元素互换位置，然后删去末尾元素。

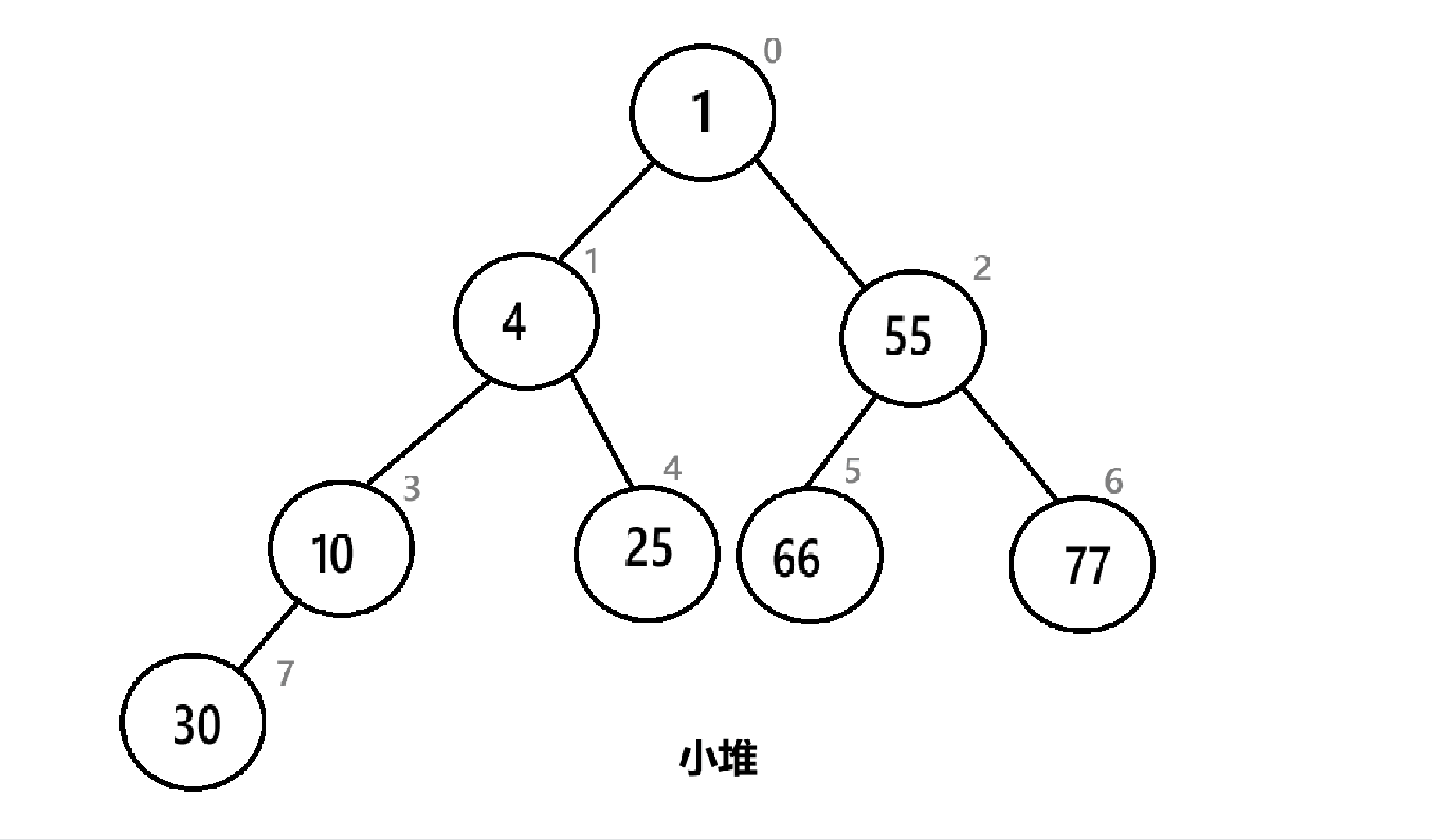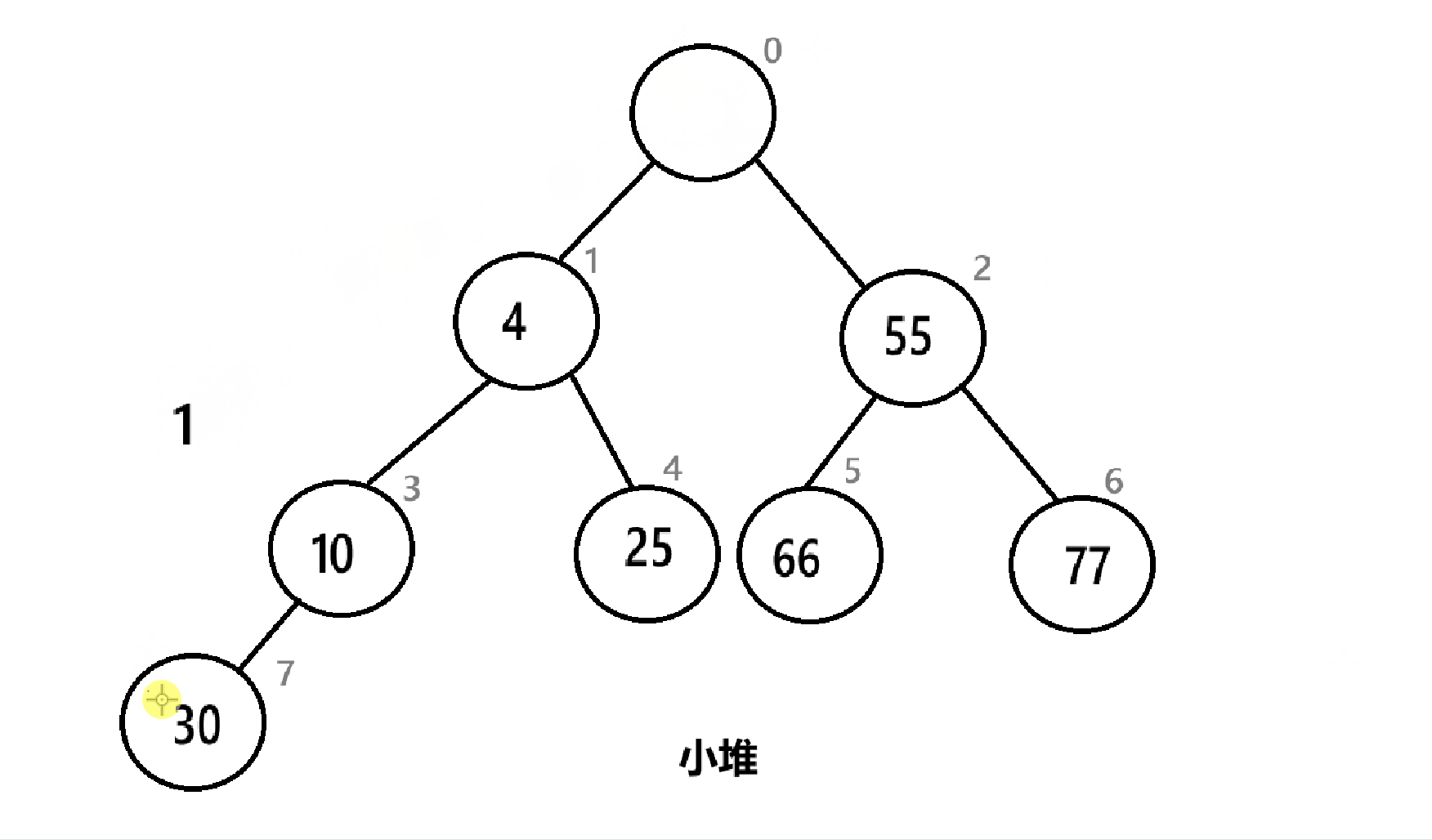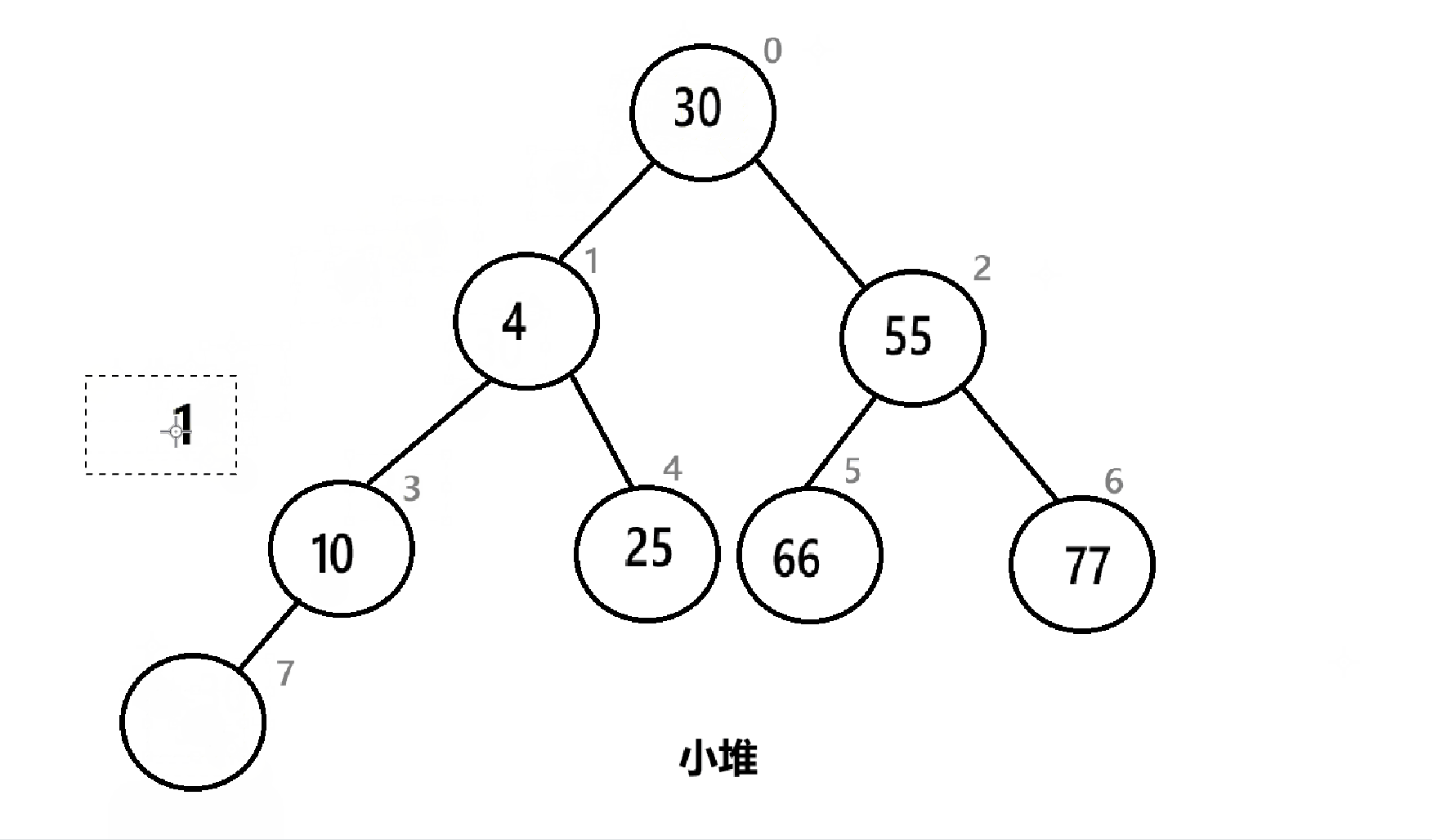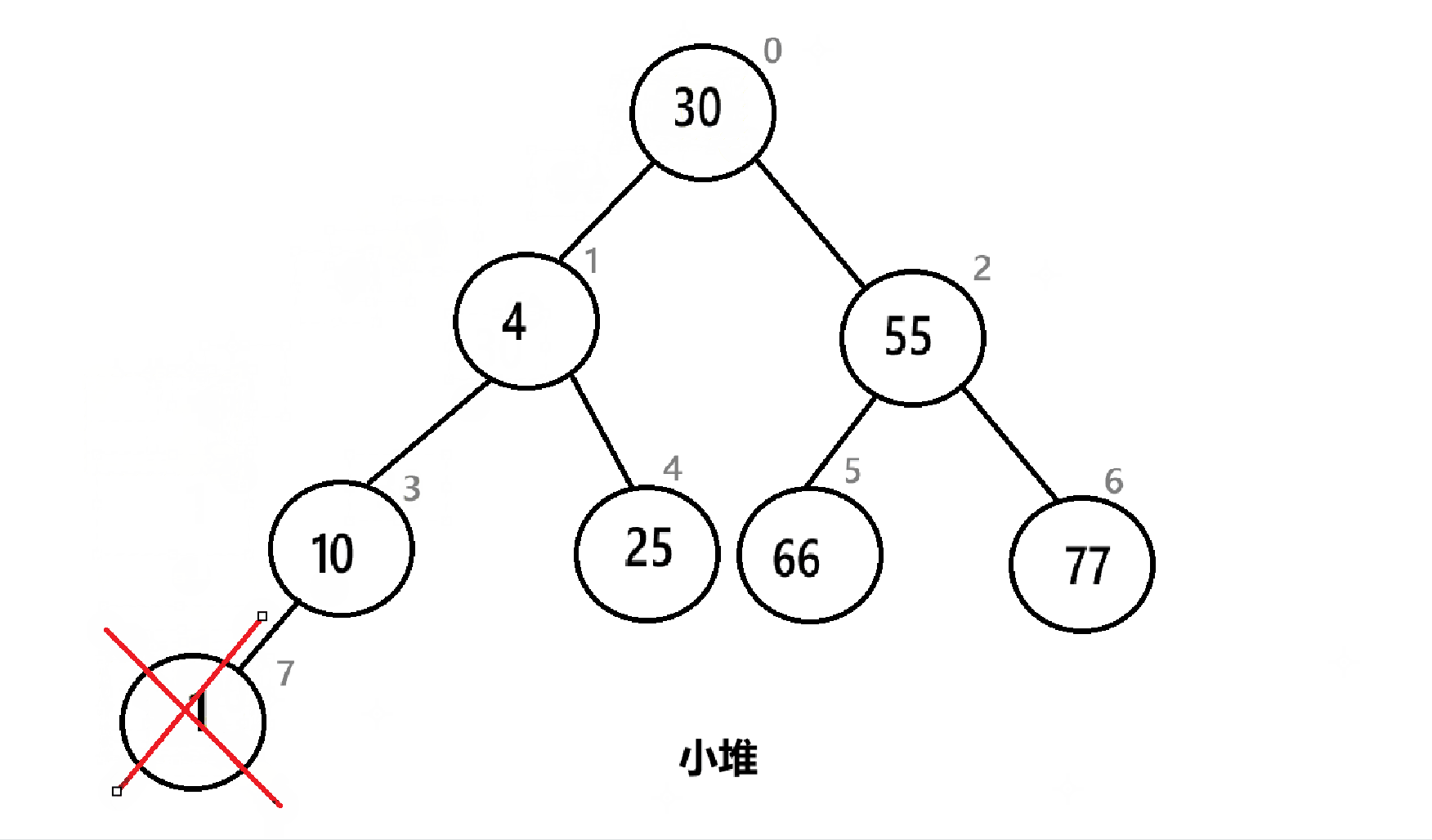
然后堆顶放了一个比较大的值，需要向下调整，让其回到正确的位置。具体算法见4.2.7

下面是删除堆顶的代码：

void HeapPop(Heap* hp)
{assert(!HeapEmpty(hp));//交换位置Swap(&hp->arr[0], &hp->arr[hp->size - 1]);//删除最后一个元素hp->size--;//向下调整AdjustDown(hp->arr, 0, hp->size);
}

4.2.7、向下调整

以下是算法的具体实现：

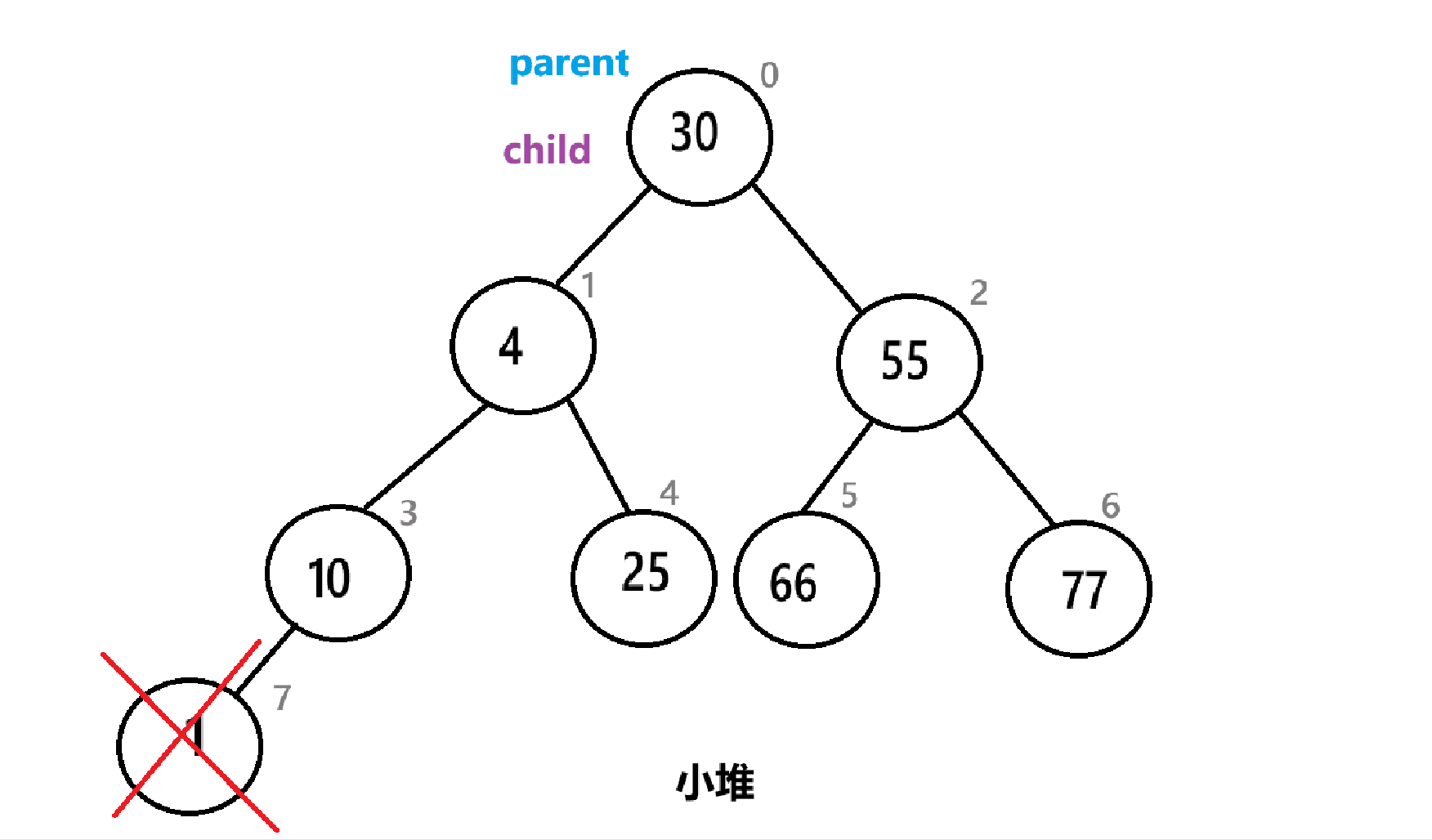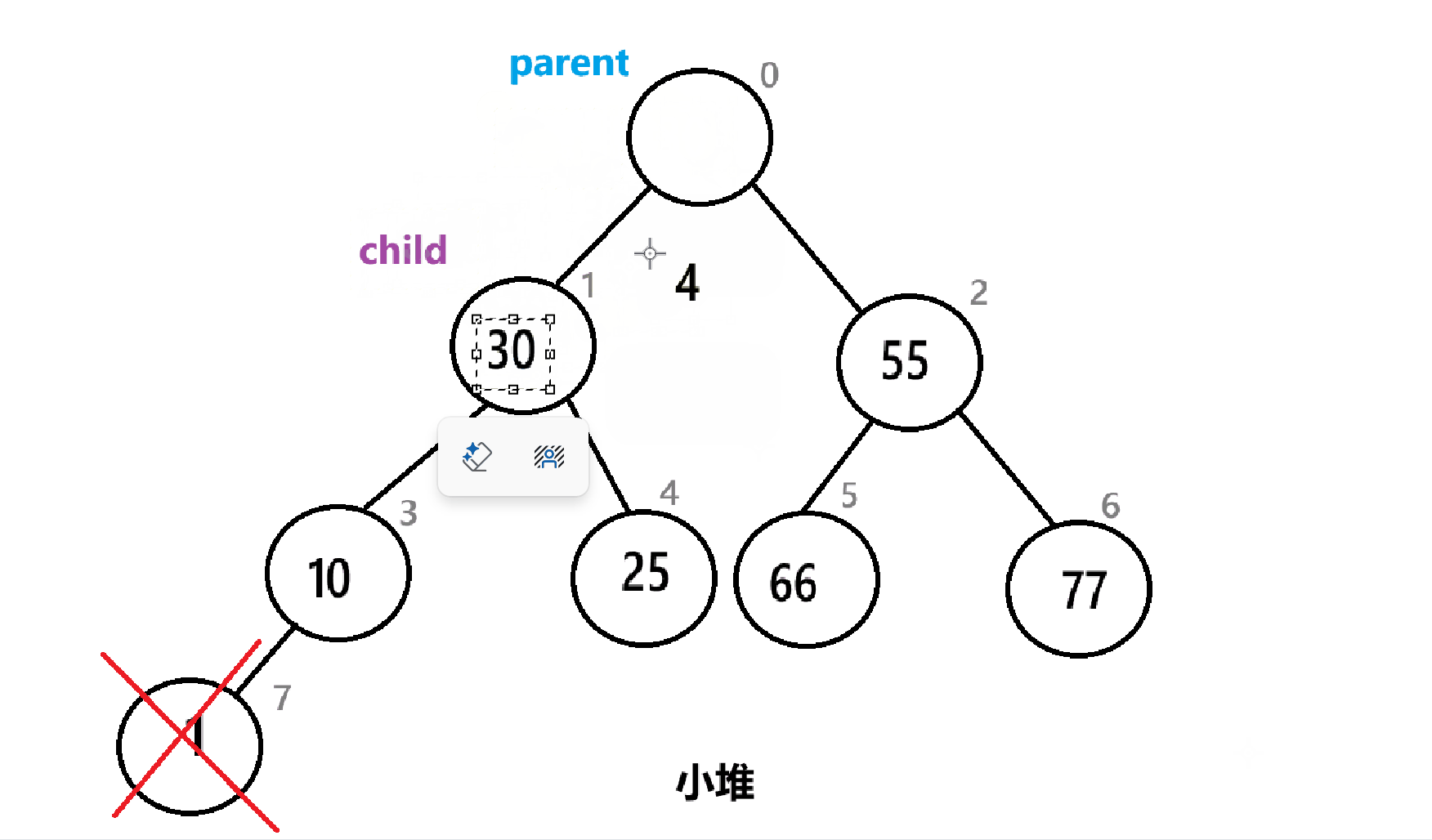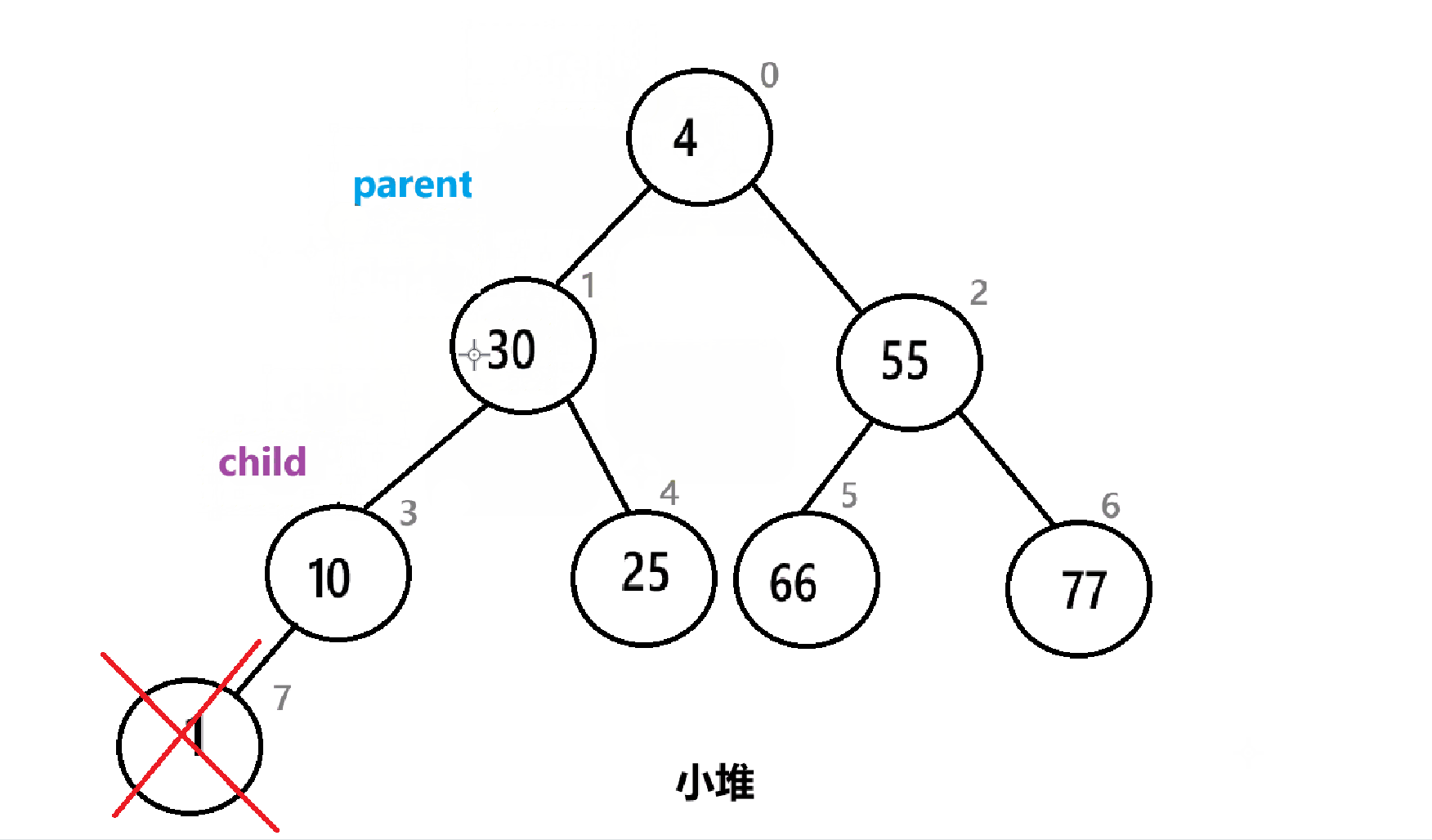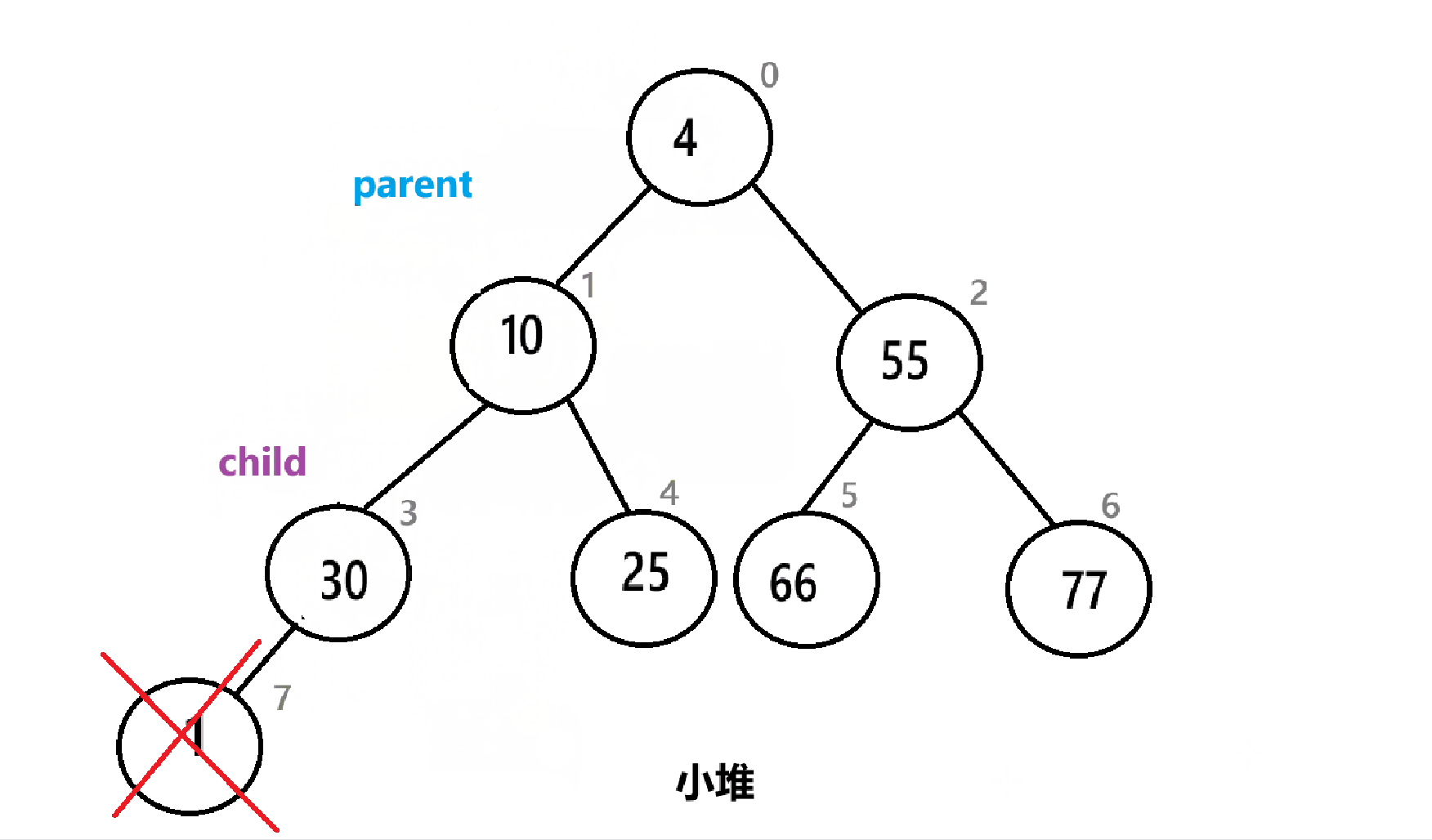
这里要说明以下，我么建的是小堆，所以在选择孩子的时候需要选择孩子中较小的那个，而且需要考虑边界问题。

void AdjustDown(HeapDataType* arr, int parent, int n)
{assert(arr);int child = parent * 2 + 1;while (child < n){//先比较左右孩子,同时需要考虑边界问题if (arr[child + 1] < arr[child] && child+1 < n){child = child + 1;}//孩子和父母比较if (arr[parent] > arr[child]){Swap(&arr[parent], &arr[child]);parent = child;child = 2 * parent + 1;}else{break;}}
}

4.2.8、取堆顶

直接返回堆顶就行了。

HeapDataType HeapTop(Heap* hp)
{assert(!HeapEmpty(hp));return hp->arr[0];
}

4.2.9、销毁

销毁堆需要将那个数组释放，还要将size 和 capacity置为0.

void HeapDestory(Heap* hp)
{assert(hp);if (hp->arr)free(hp->arr);hp->arr = NULL;hp->size = hp->capacity = 0;
}

4.3、堆排序

4.3.1、核心思想

以小堆为例，有个非常重要的特性——堆顶永远是最小值！我们只需要取堆顶，删堆顶，再取堆顶，再删堆顶……就会得到一个升序序列！如果你想得到一个降序序列，只需要将小堆换成大堆即可。

4.3.2、具体实现

所以堆排序很明显：

void HeapSort1(int* arr, int n)
{assert(arr);//建堆Heap hp;HeapInit(&hp);for (int i = 0; i < n; i++){HeapPush(&hp, arr[i]);}for (int i = 0; i < n; i++){//取堆顶arr[i] = HeapTop(&hp);//删堆顶HeapPop(&hp);}//销毁堆HeapDestory(&hp);
}

4.3.3、真正的堆排序

显然，在实际应用中，不可能为了一个堆排序而专门写一个堆的底层逻辑，所以4.3.2中的堆排序是不切实际的，我们真正的堆排序采用的是堆的思想——堆顶为最值

首先，需要在原数组上进行建堆，不能开辟新的空间！就需要对该数组使用向下调整算法。

如图，为序列8 7 6 5 3 4 3 2 1的对应的“堆”。发现，向下建堆只能选择左右子树的一个方向进行，显然是不可能建堆的，所以，向下调整不能只实行一次。

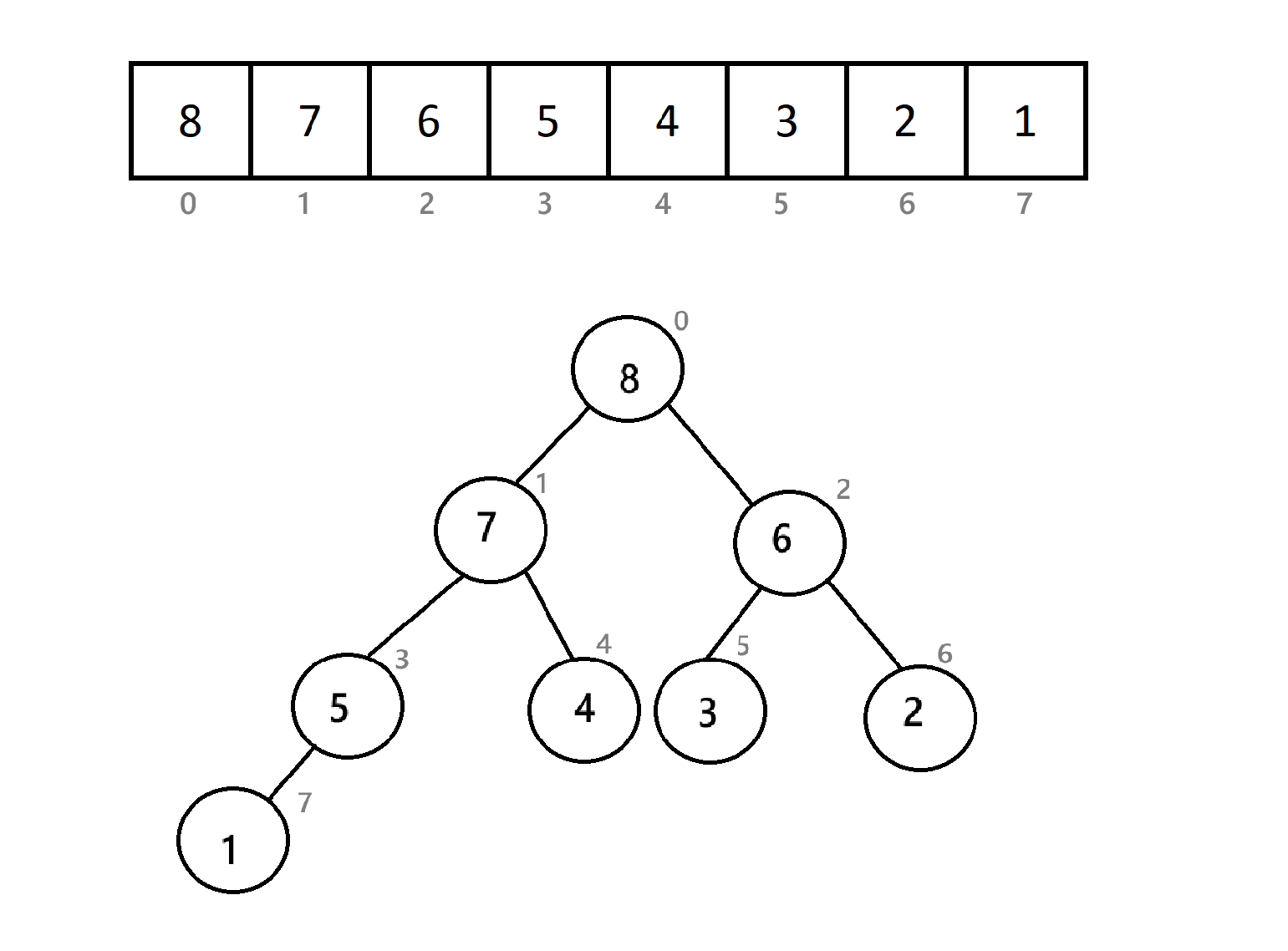
以下为向下调整建堆的全部过程：

可以看到，我们从倒数第二层的结点开始一个节点一个节点进行向下调整，最后就完成了建堆。那如果是向上调整呢？就从根节点开始，一个节点一个节点进行向上调整。

在建堆后，我们就需要进行取堆顶，删除堆顶的重复操作了，但是为了避免开辟新的空间，要把堆顶放到数组的末尾（反正最后删堆顶的时候size--，后面的空间也没用）

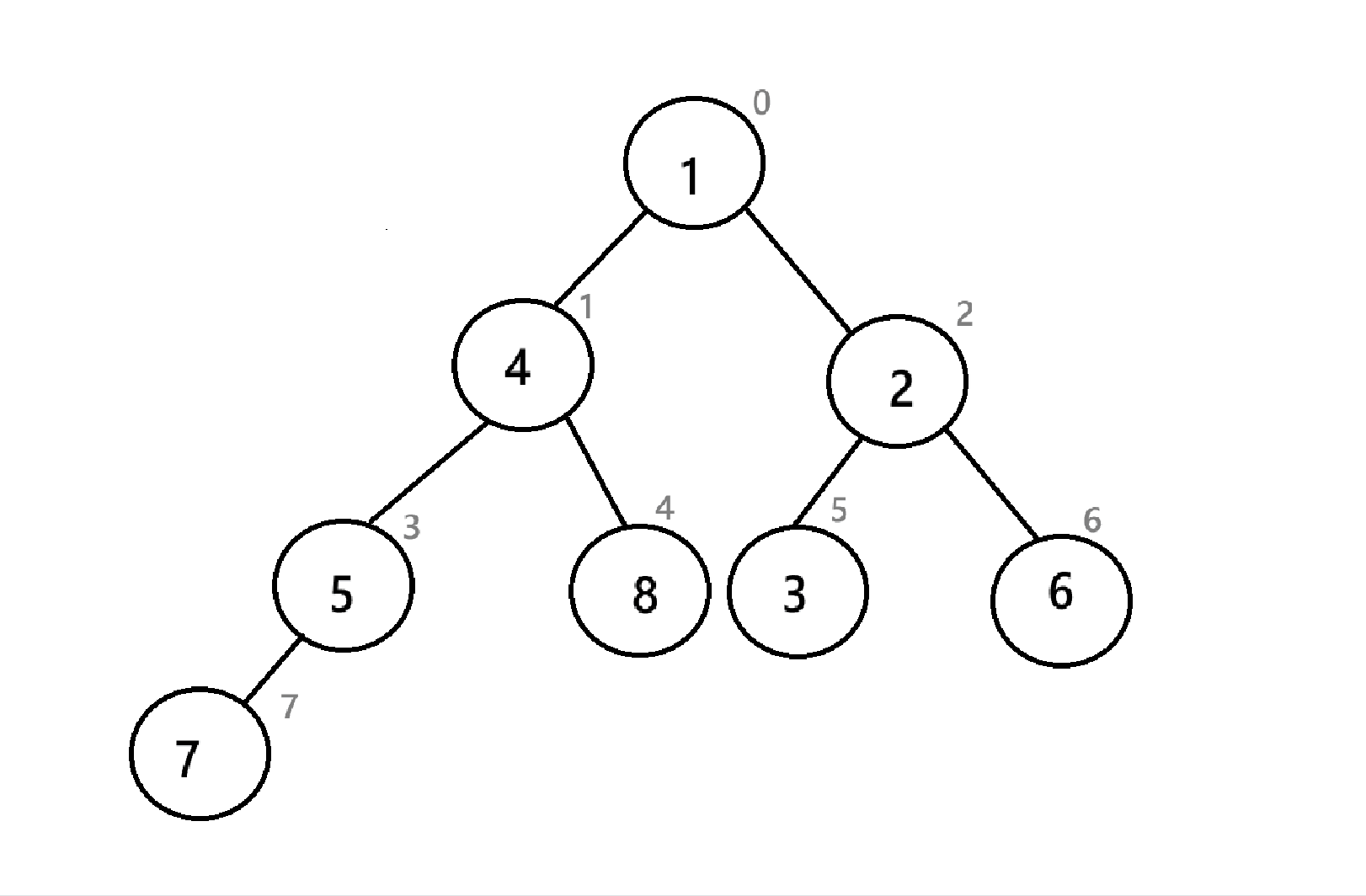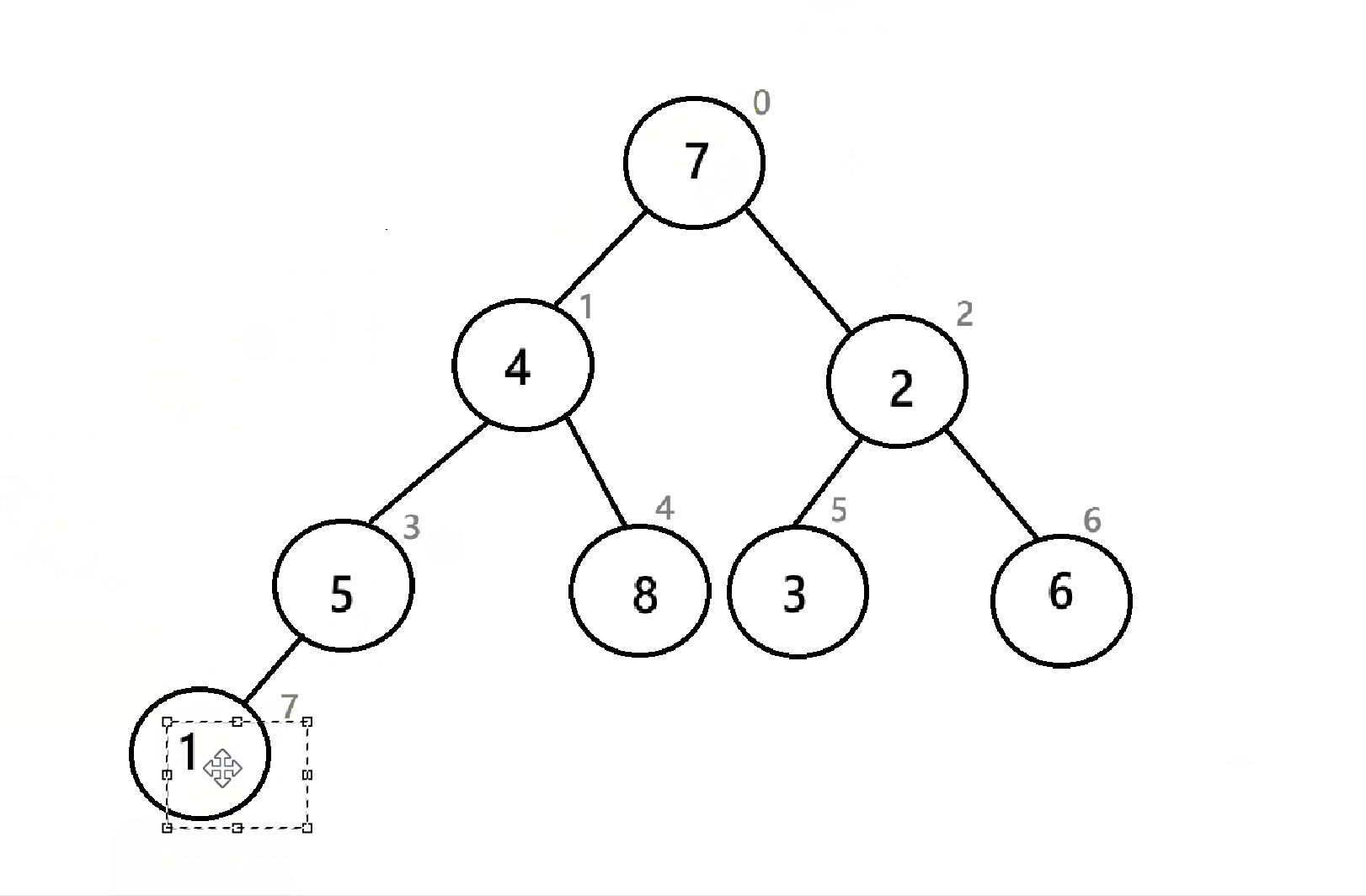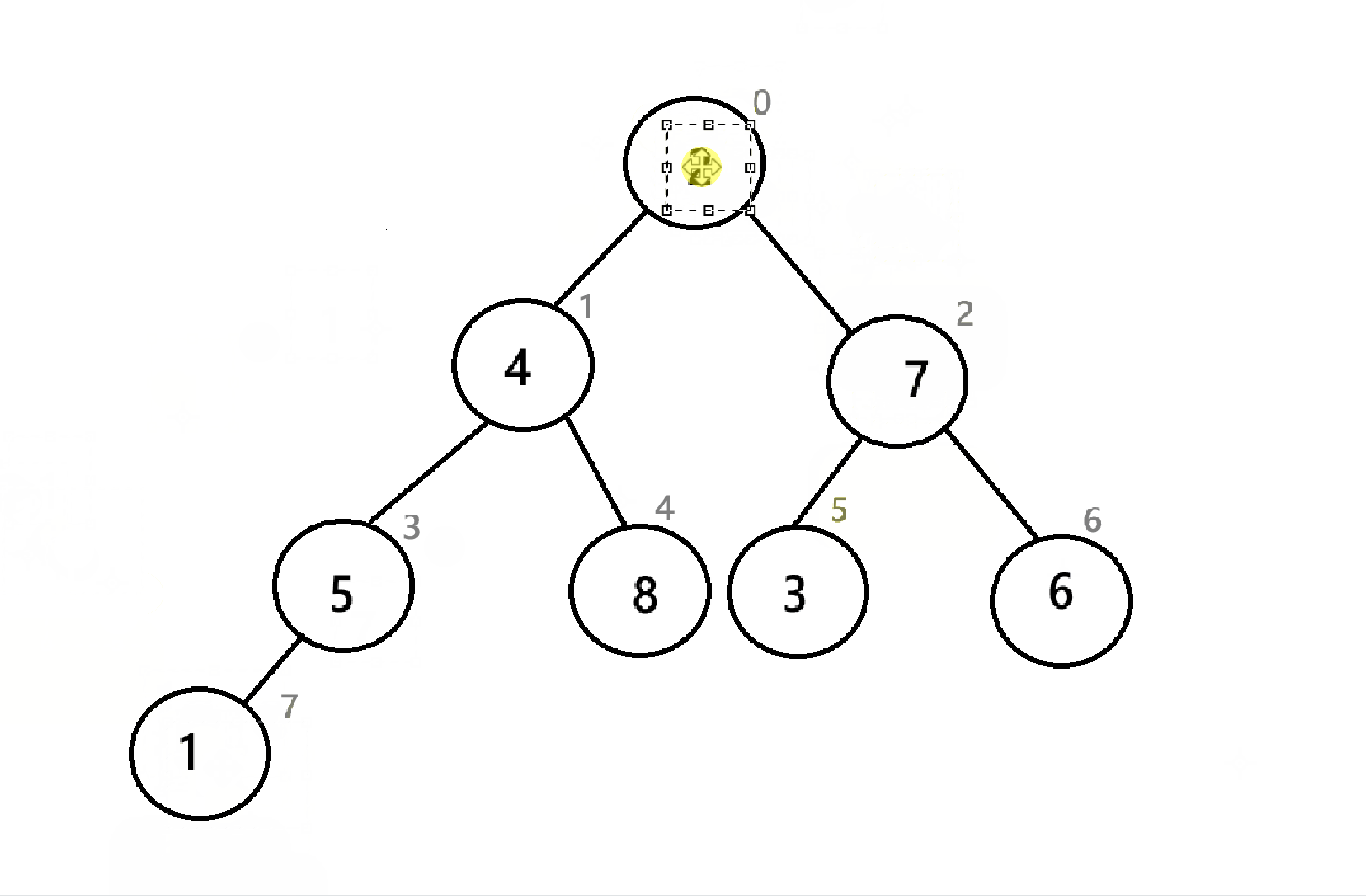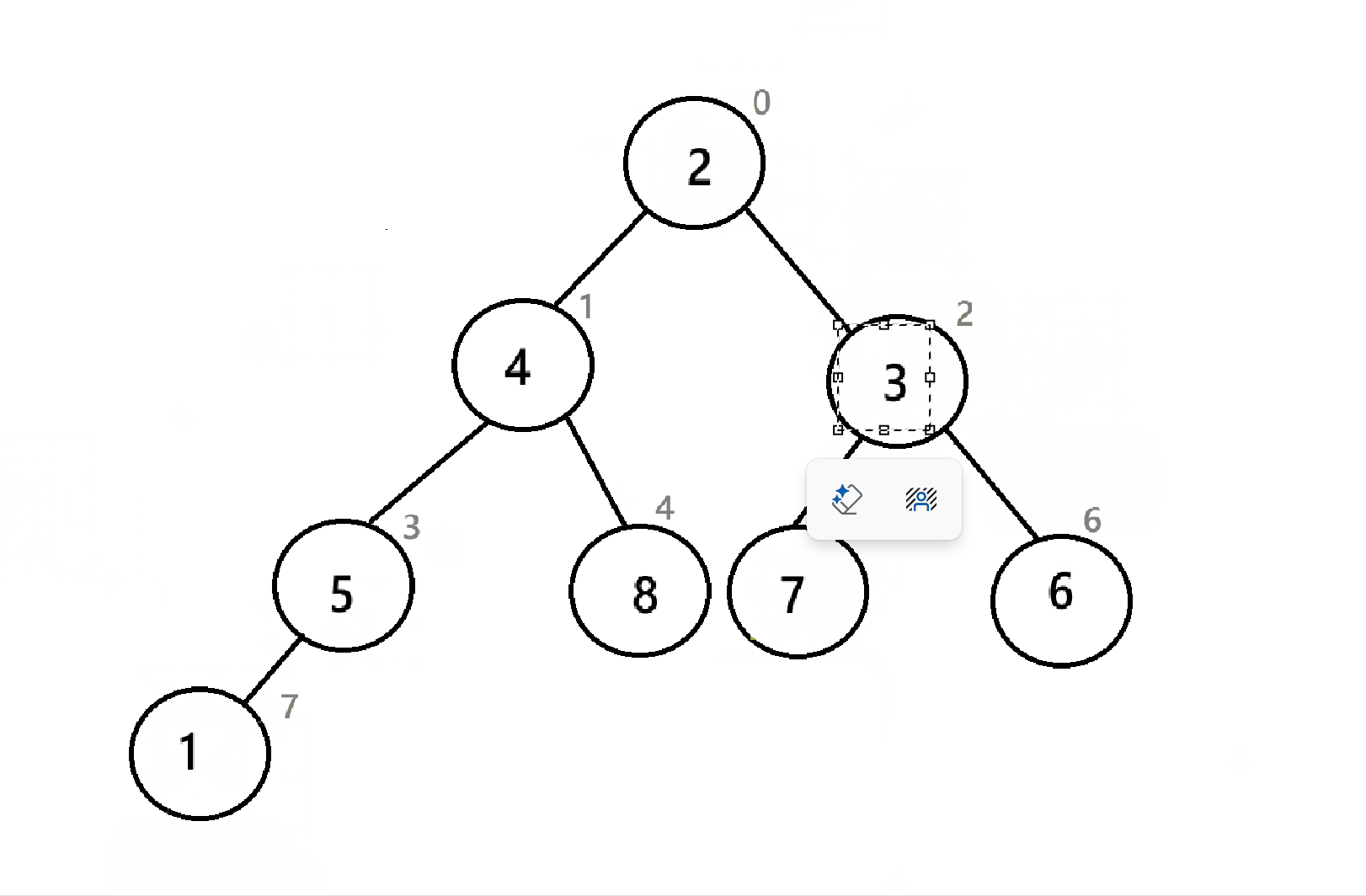
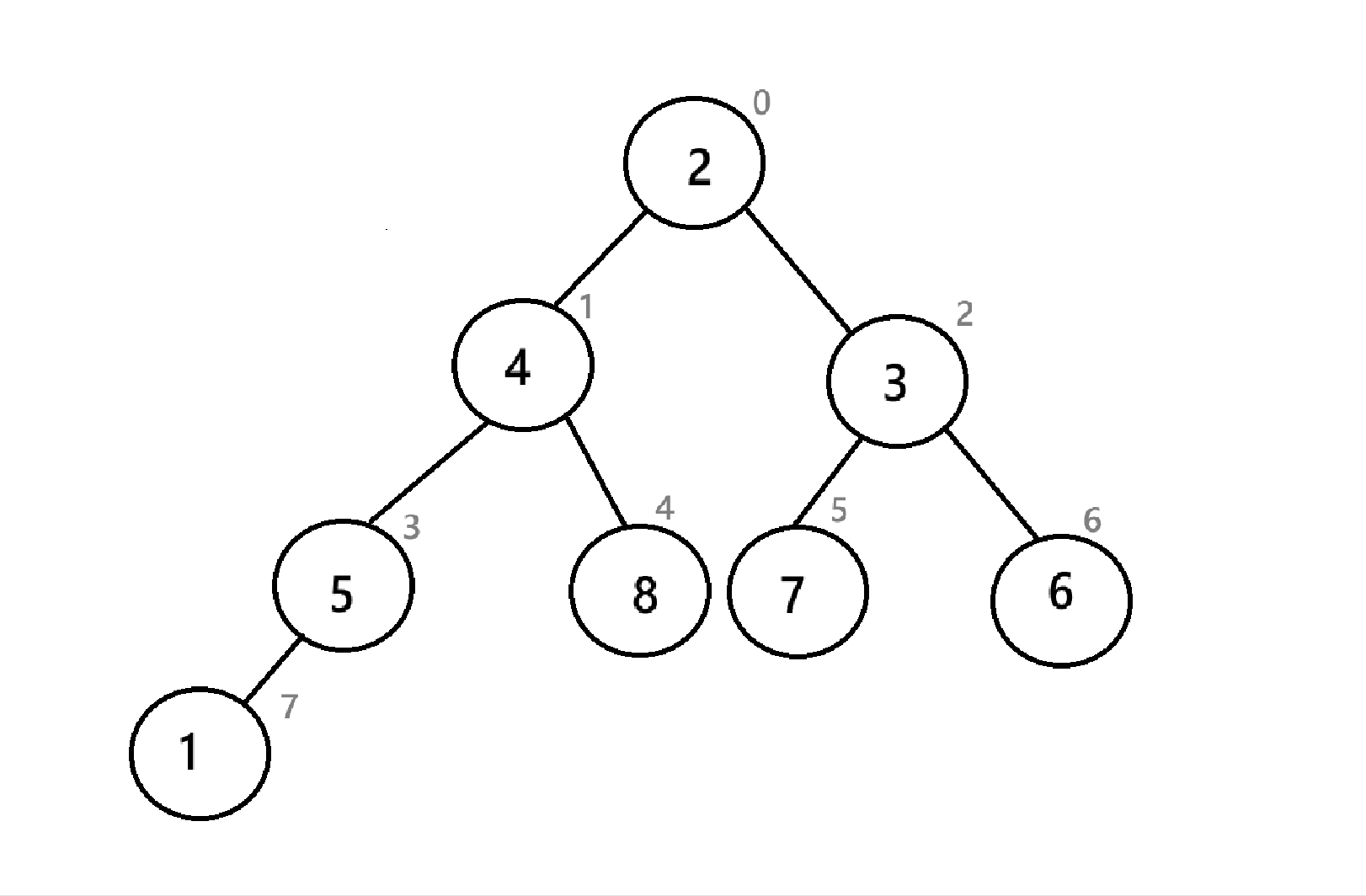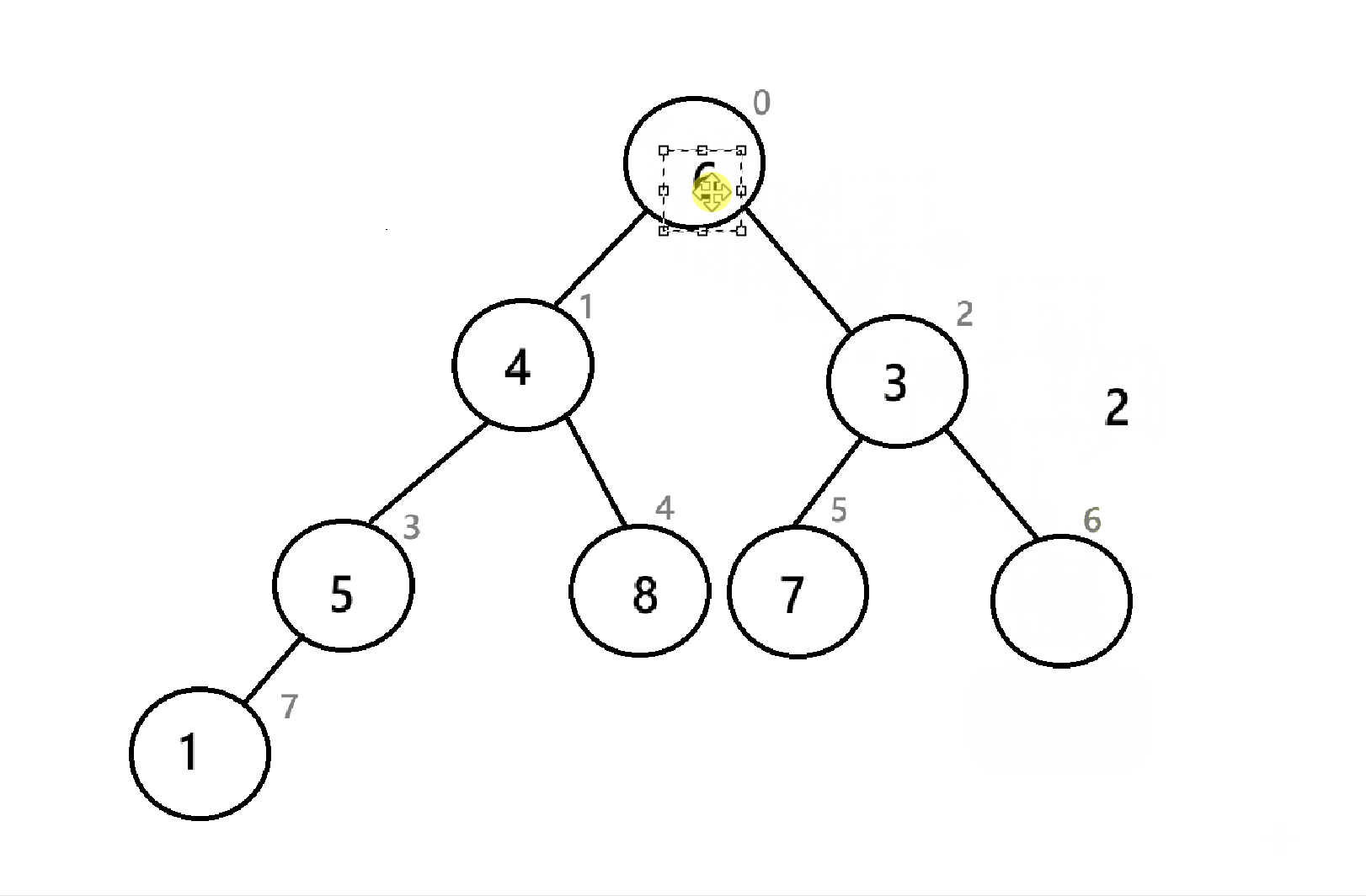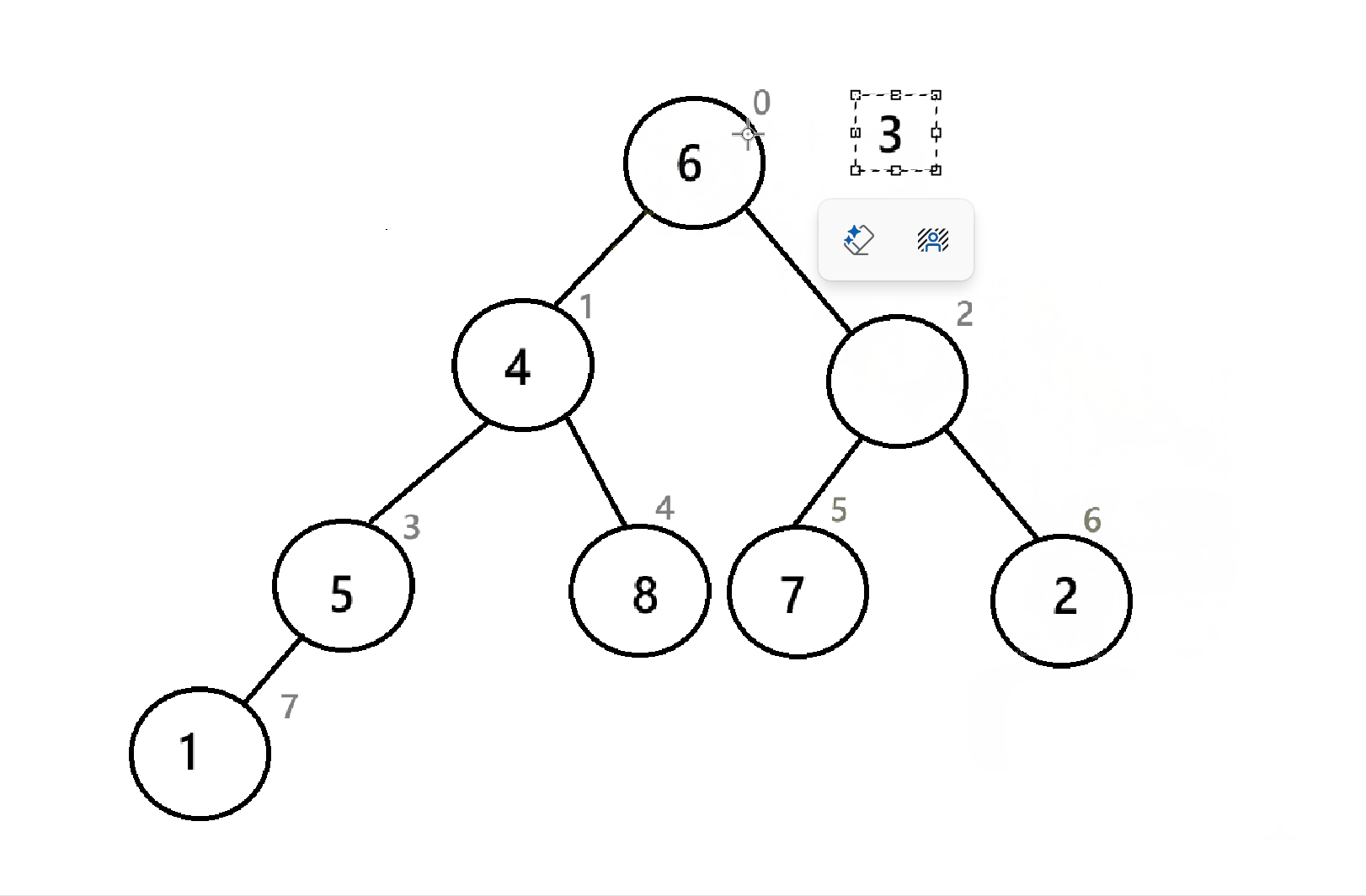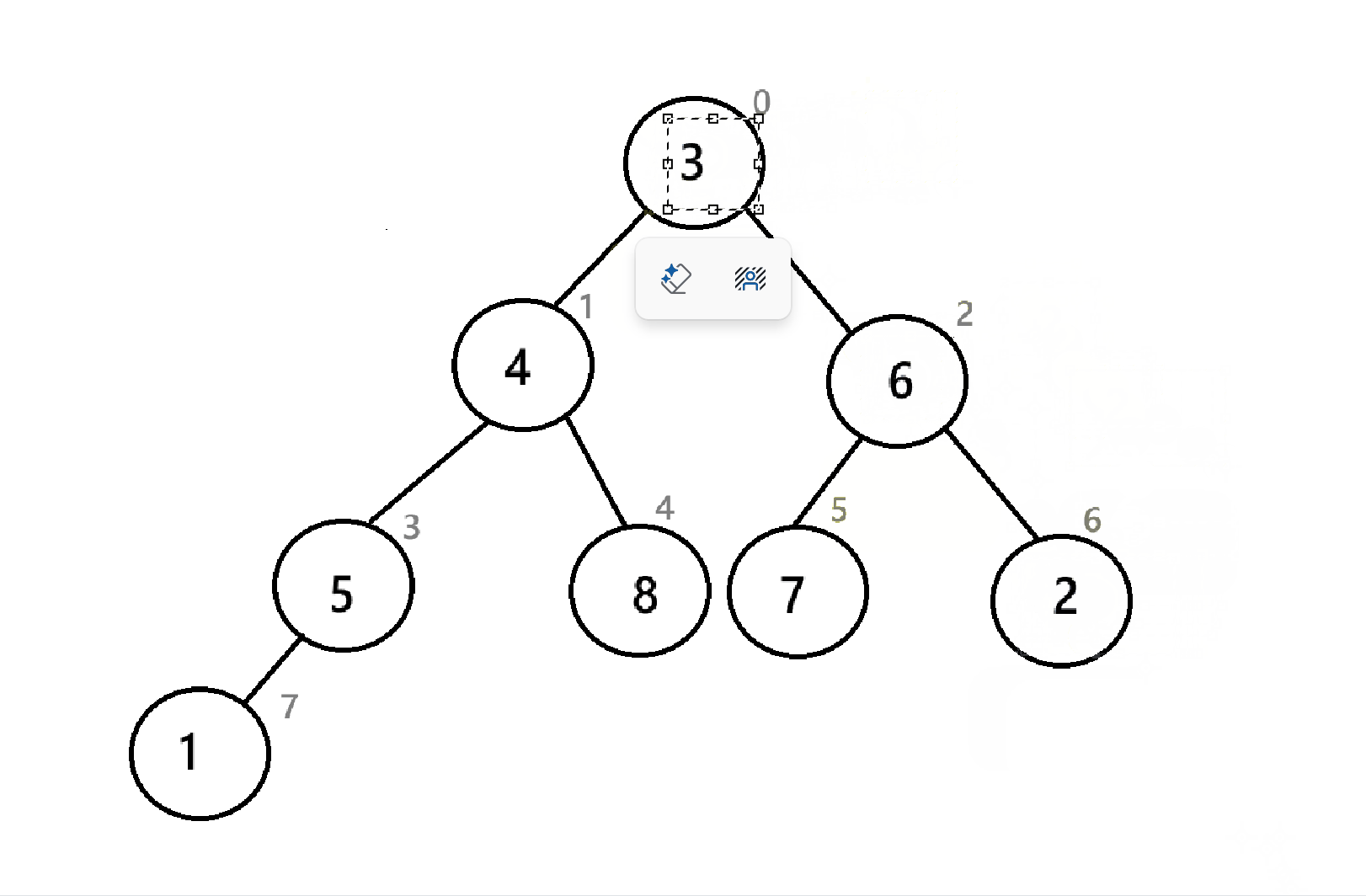
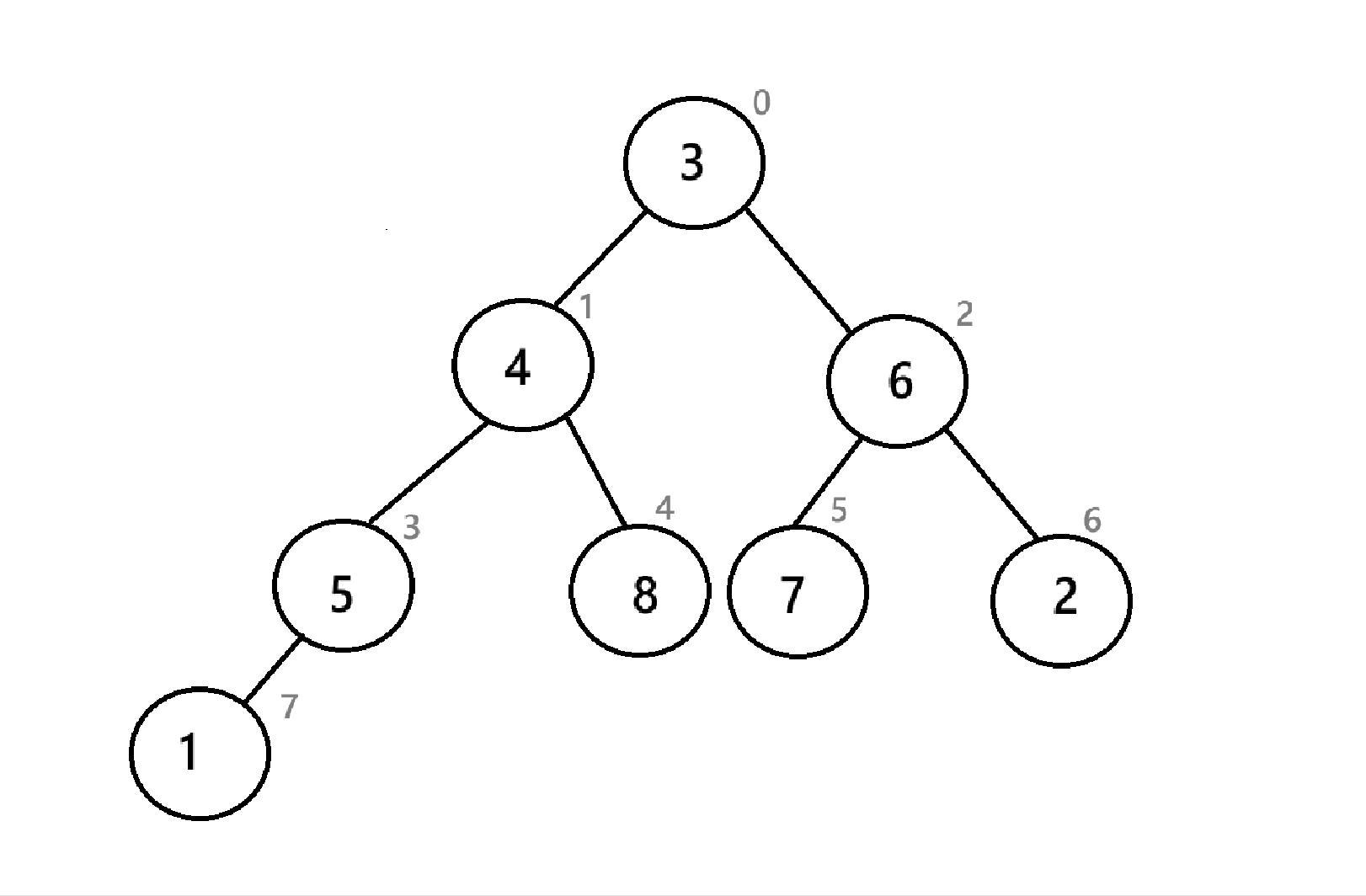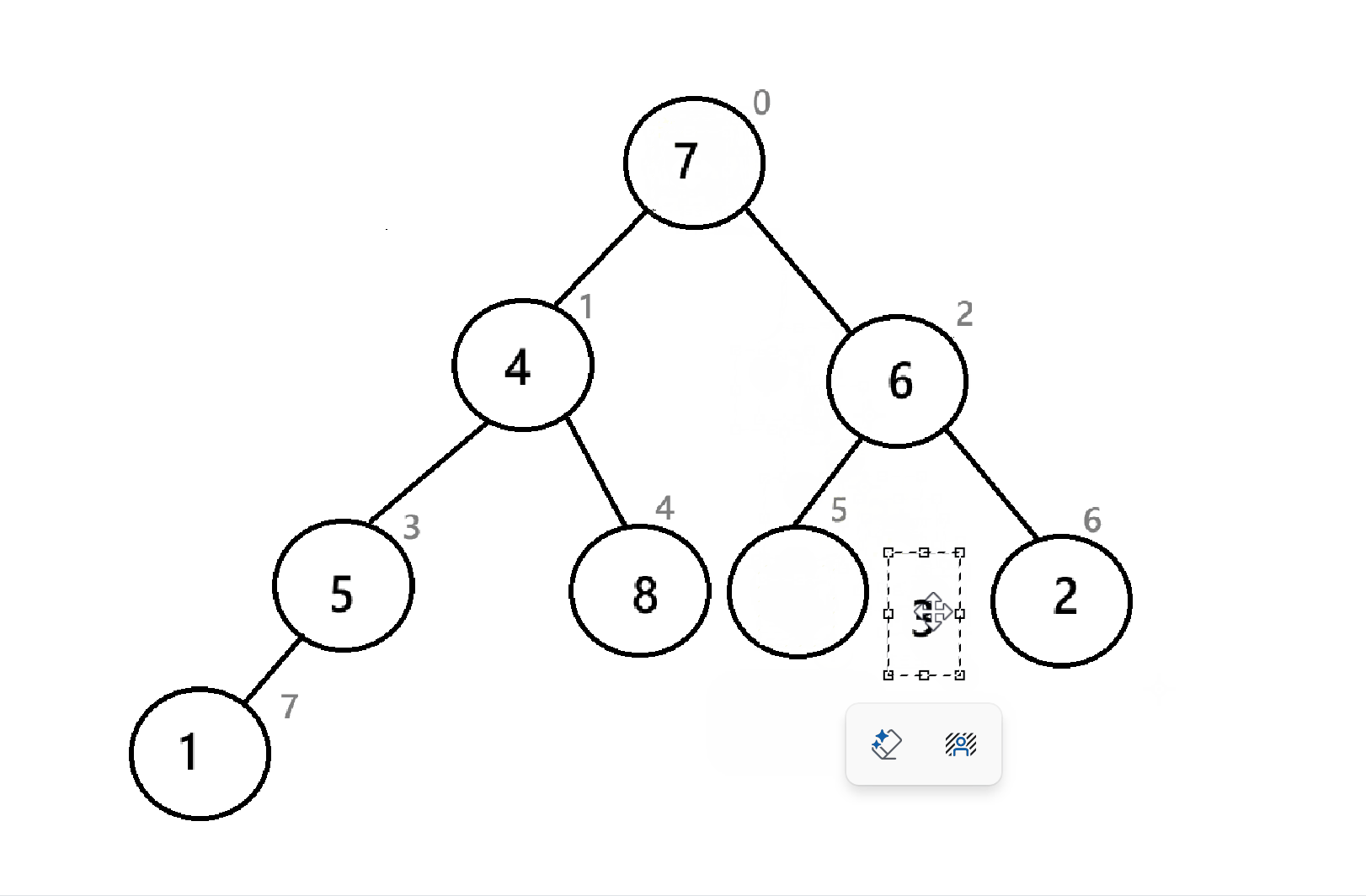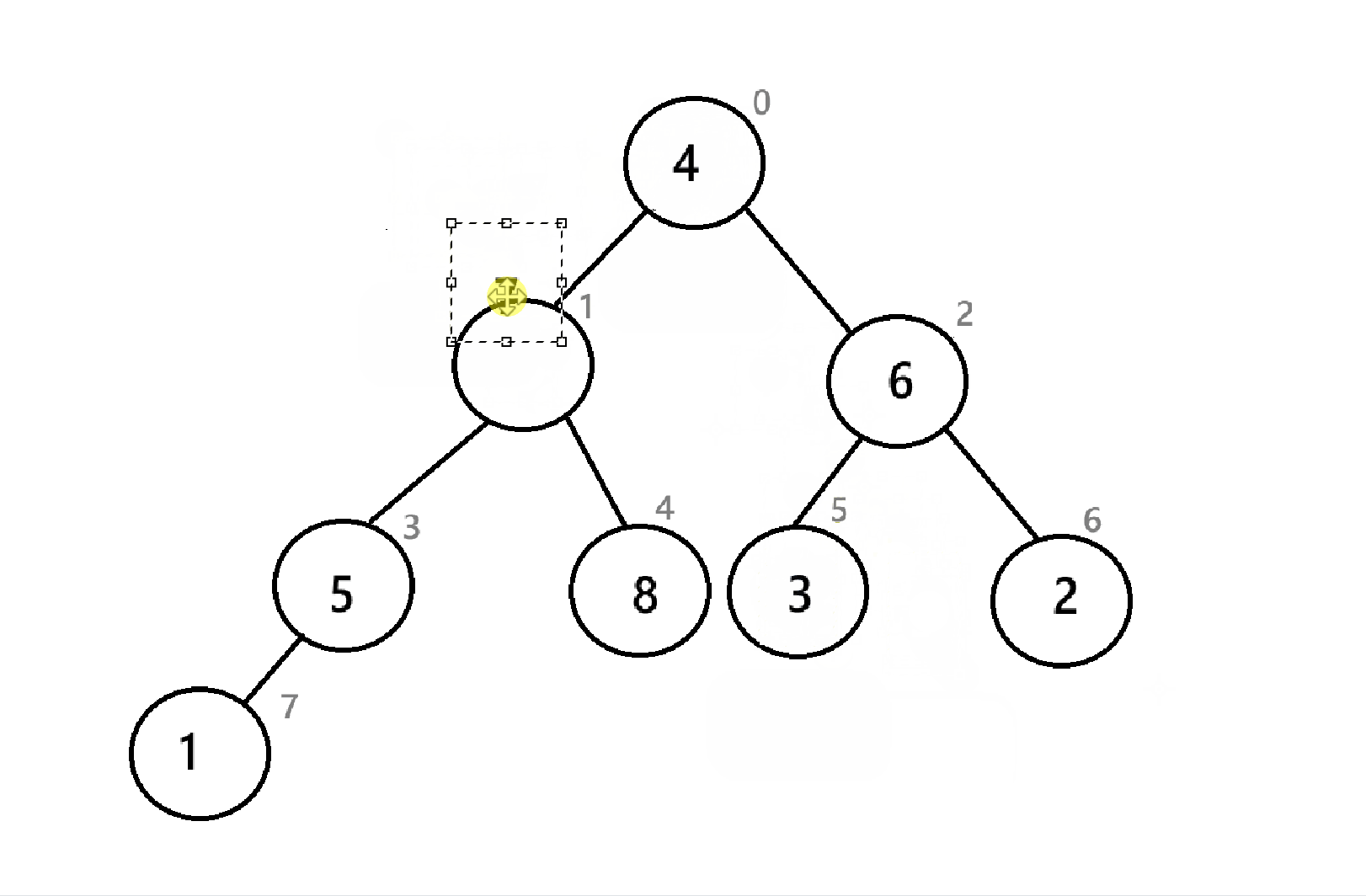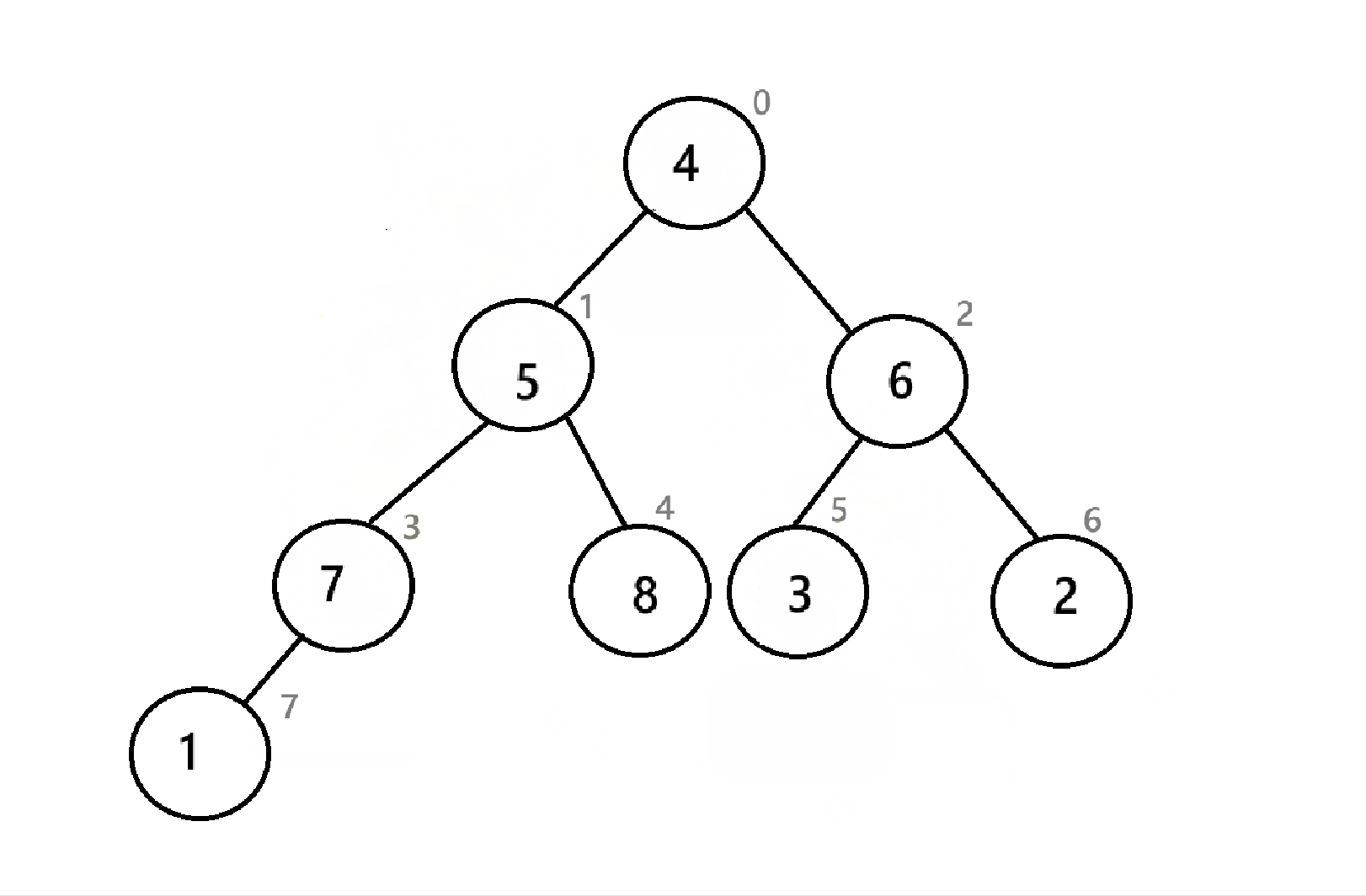
可以看到，经过三次操作，数组末尾已经是一个降序序列了，与4.3.2的堆排序不同的是，这里的小堆创建出来的是降序，而4.3.2中创造出来的是升序，这说明升序和降序与大小堆没有直接关系，而是取决于你把取出来的堆顶怎么放。

下面是代码：

void HeapSort(int* arr, int n)
{assert(arr);//向下调整建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, i, n);}//取堆顶，删堆顶for (int i = 0; i < n; i++){Swap(&arr[0], &arr[n - 1-i]);AdjustDown(arr, 0, n - i-1);}
}

五、实现链式结构的二叉树

即用链表表示一颗二叉树

5.1、节点定义

typedef int TreeDataType;
typedef struct Tree
{TreeDataType data;    //数据struct Tree* left;    //左孩子struct Tree* right;   //右孩子
}Tree;

5.2、二叉树的遍历

5.2.1、前序遍历

前序遍历：先遍历跟，再遍历左子树，然后遍历右子树。简称：根左右

举个例子：

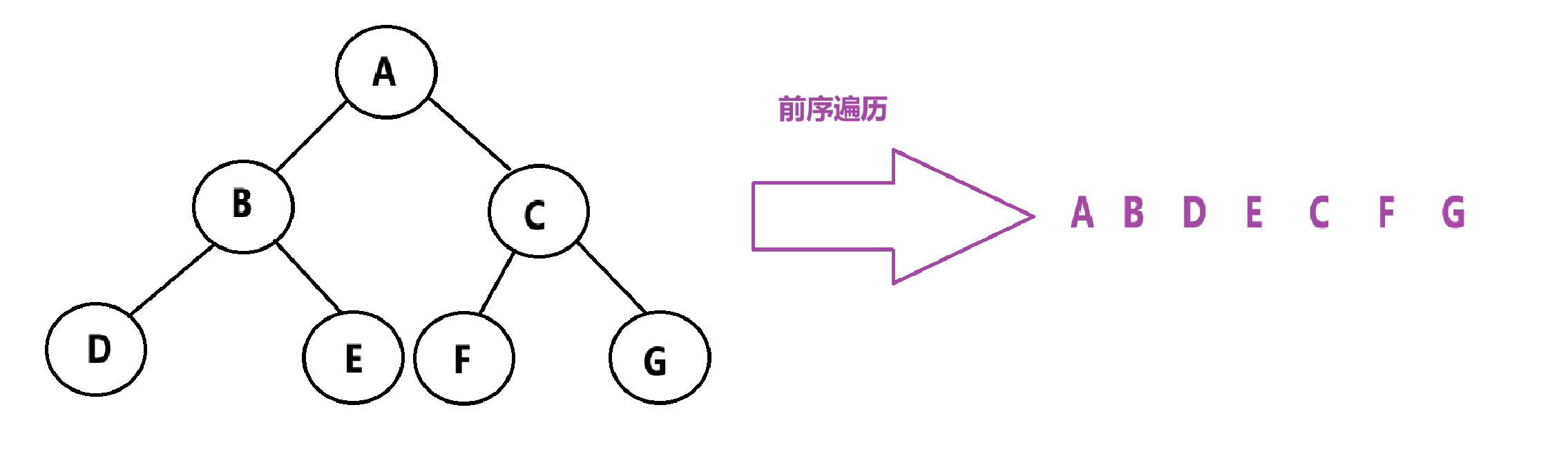
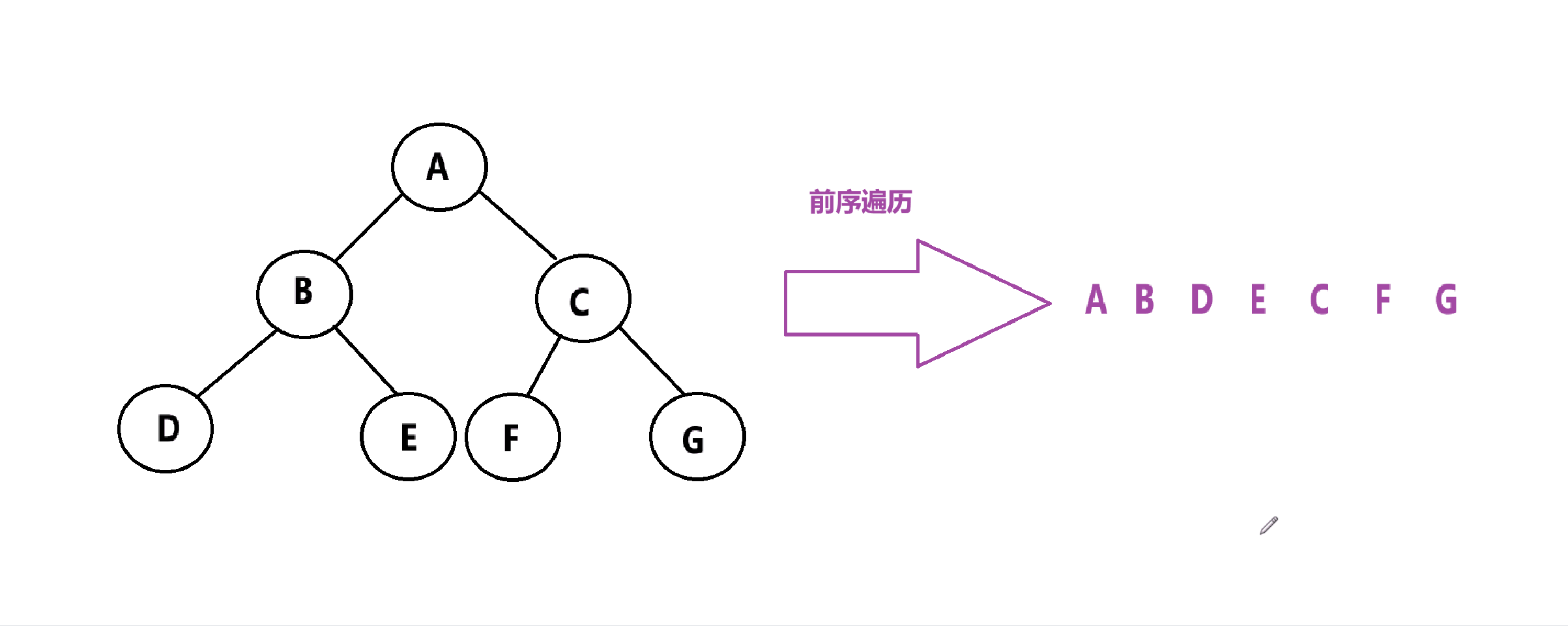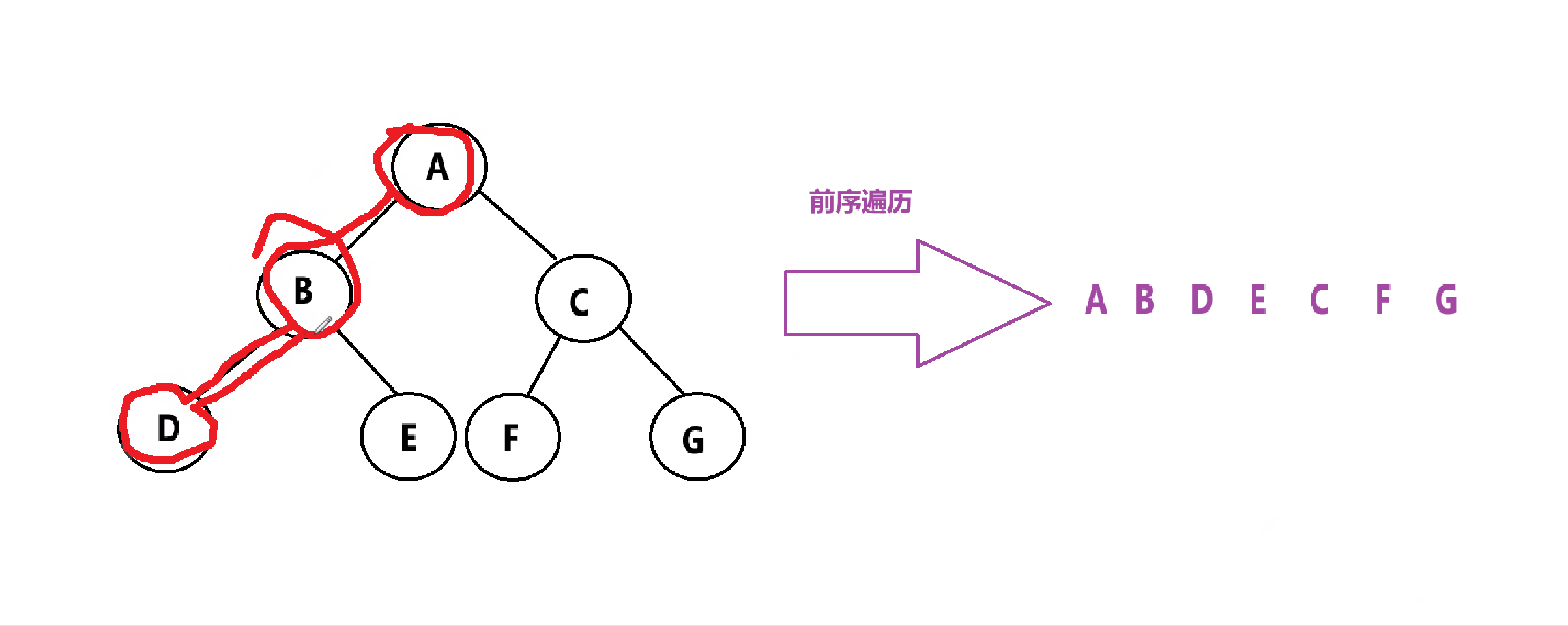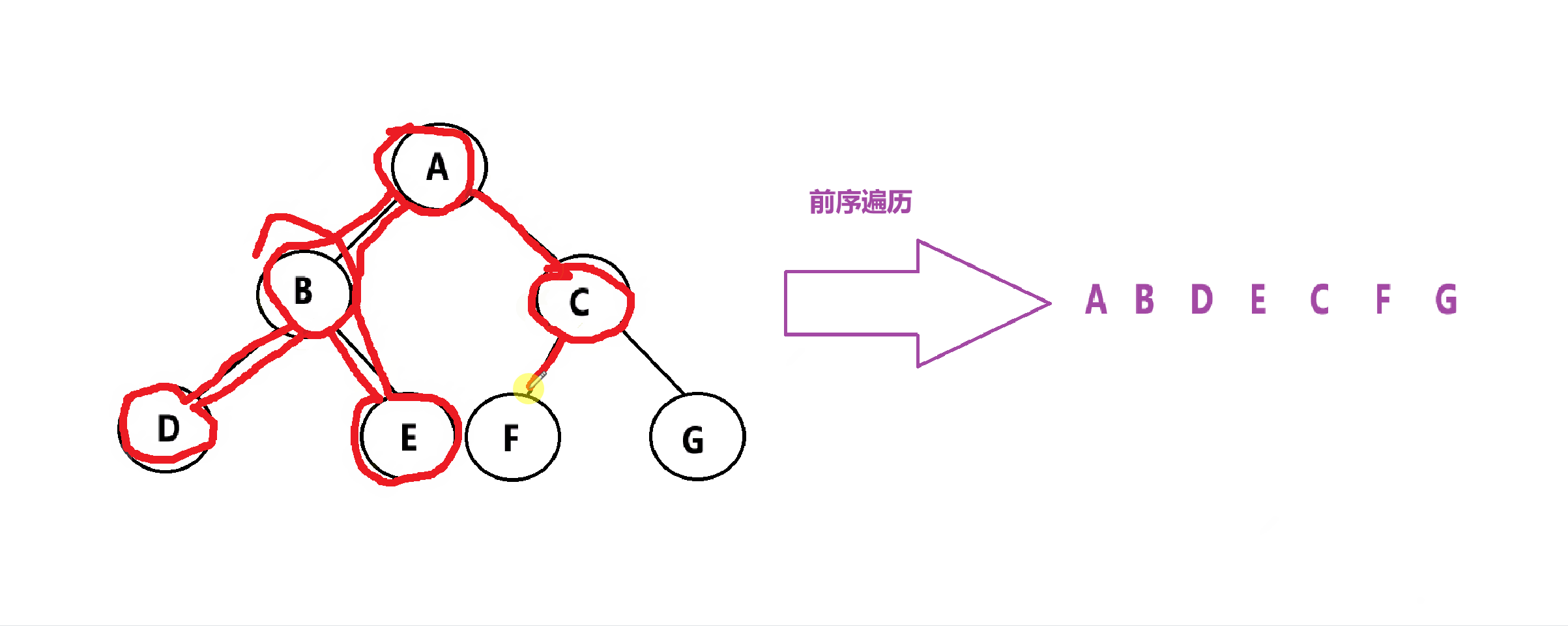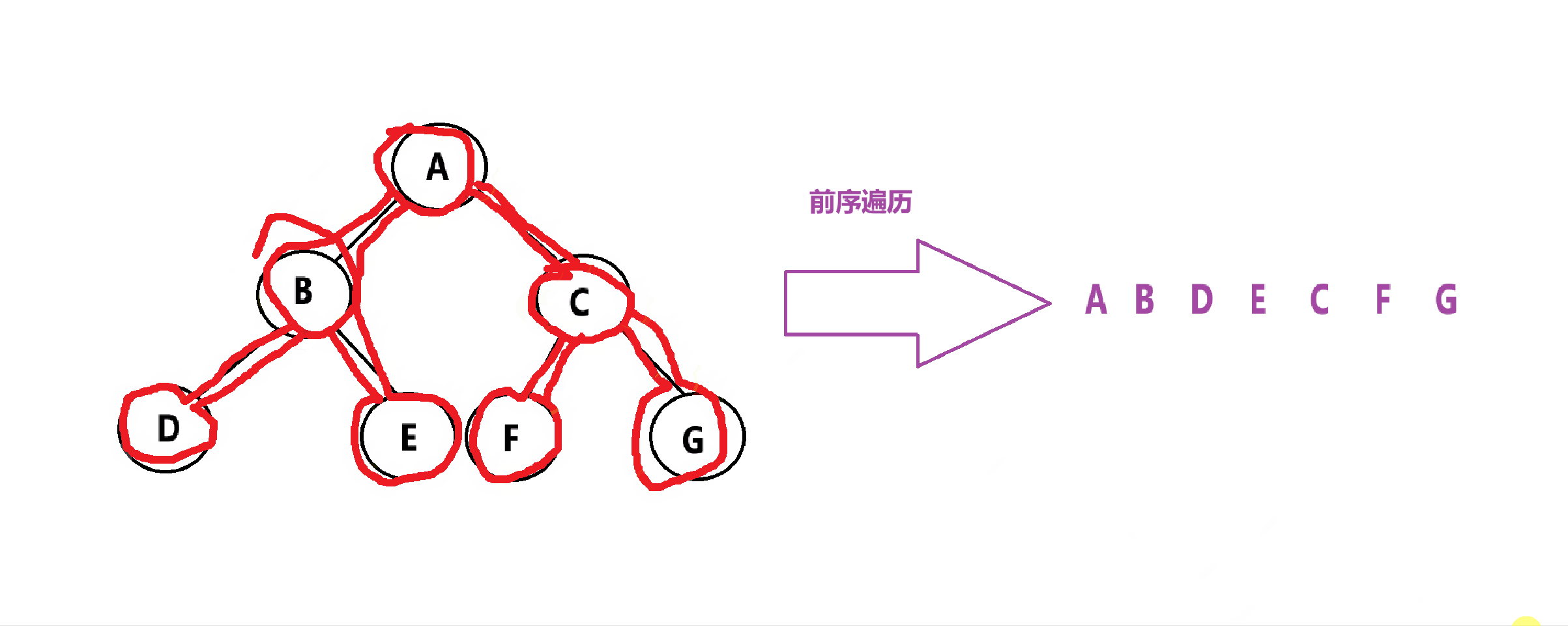
代码实现：

void PreOrder(Tree* root)
{if (root == NULL){return;}printf("%d " ,root->data);PreOrder(root->left);PreOrder(root->right);
}

5.2.2、中序遍历

中序遍历：先遍历左子树，再遍历根，最后遍历右子树。简称：左根右

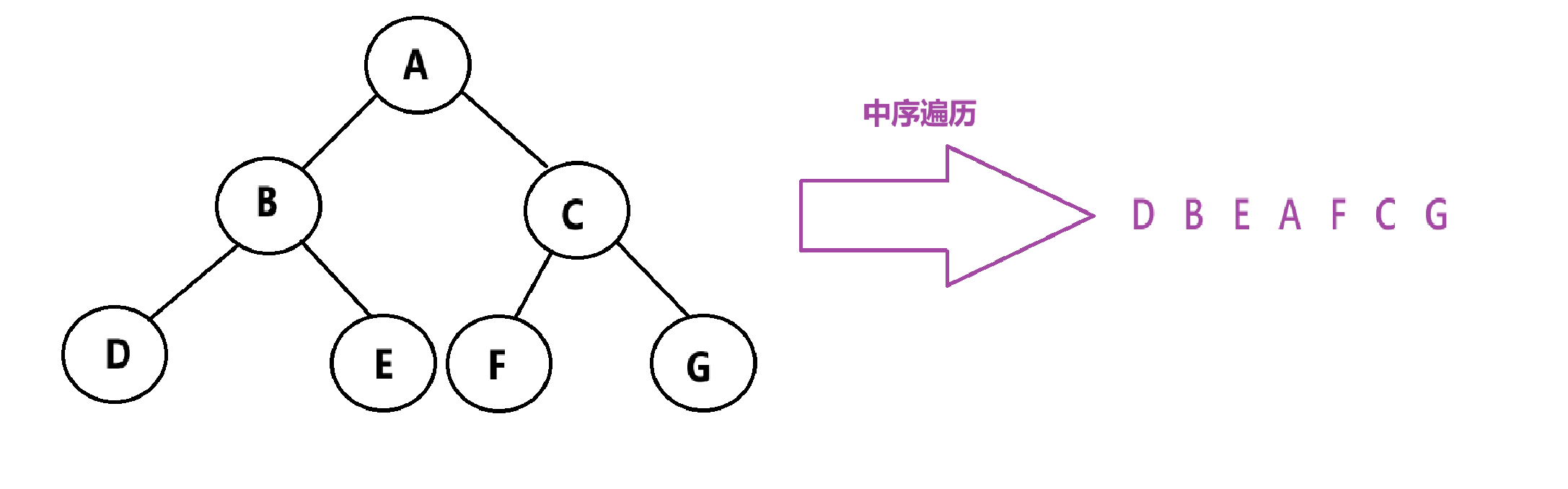
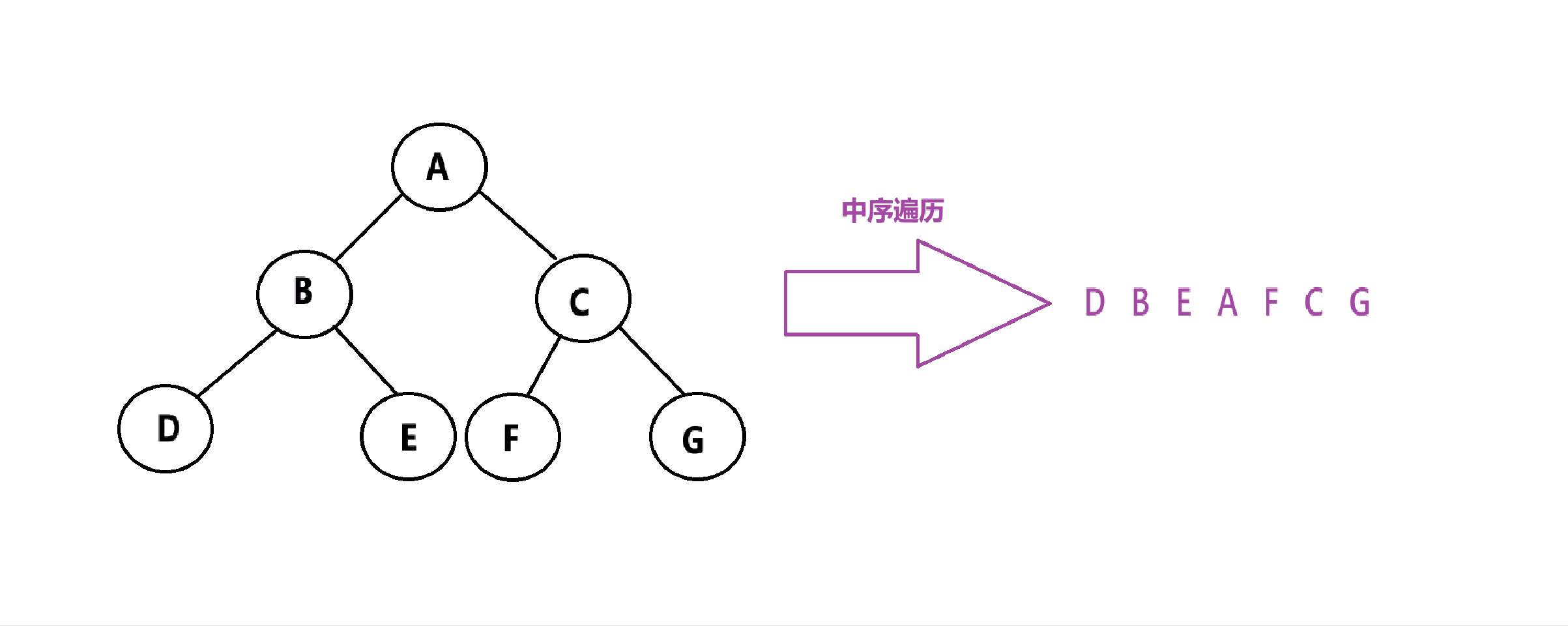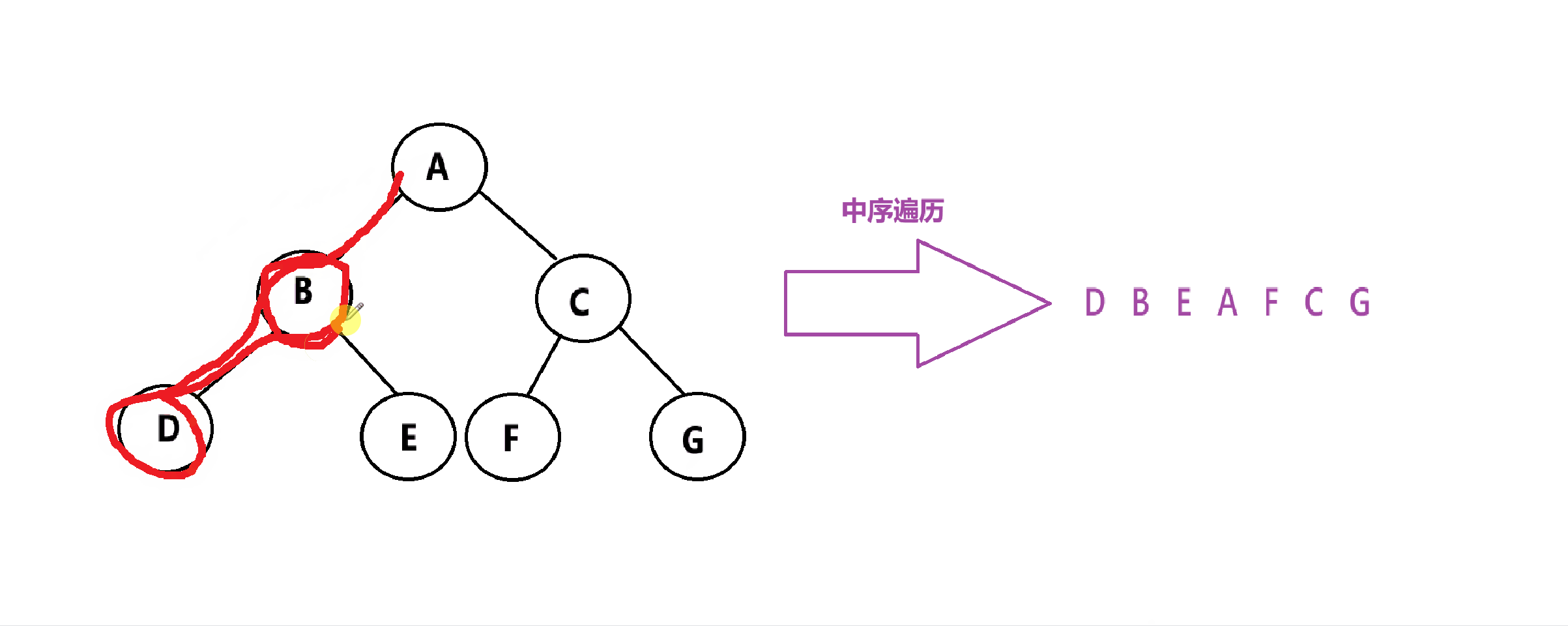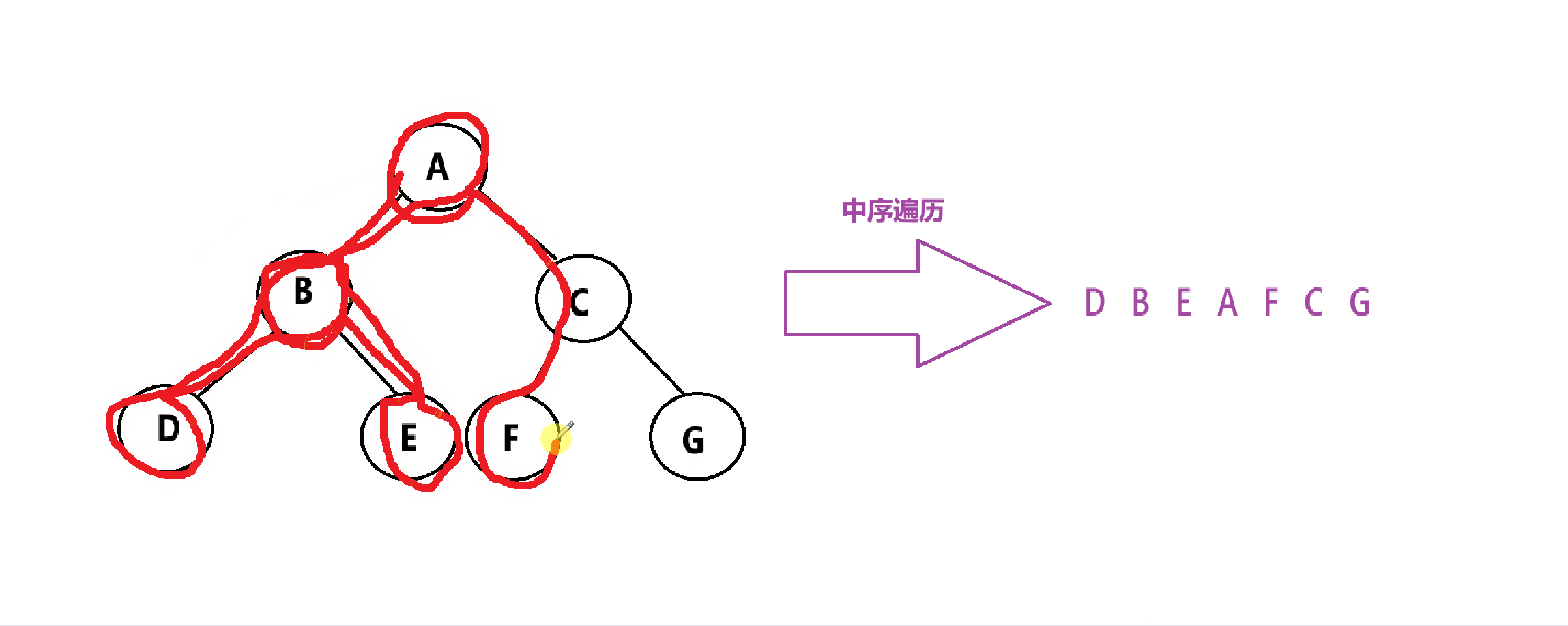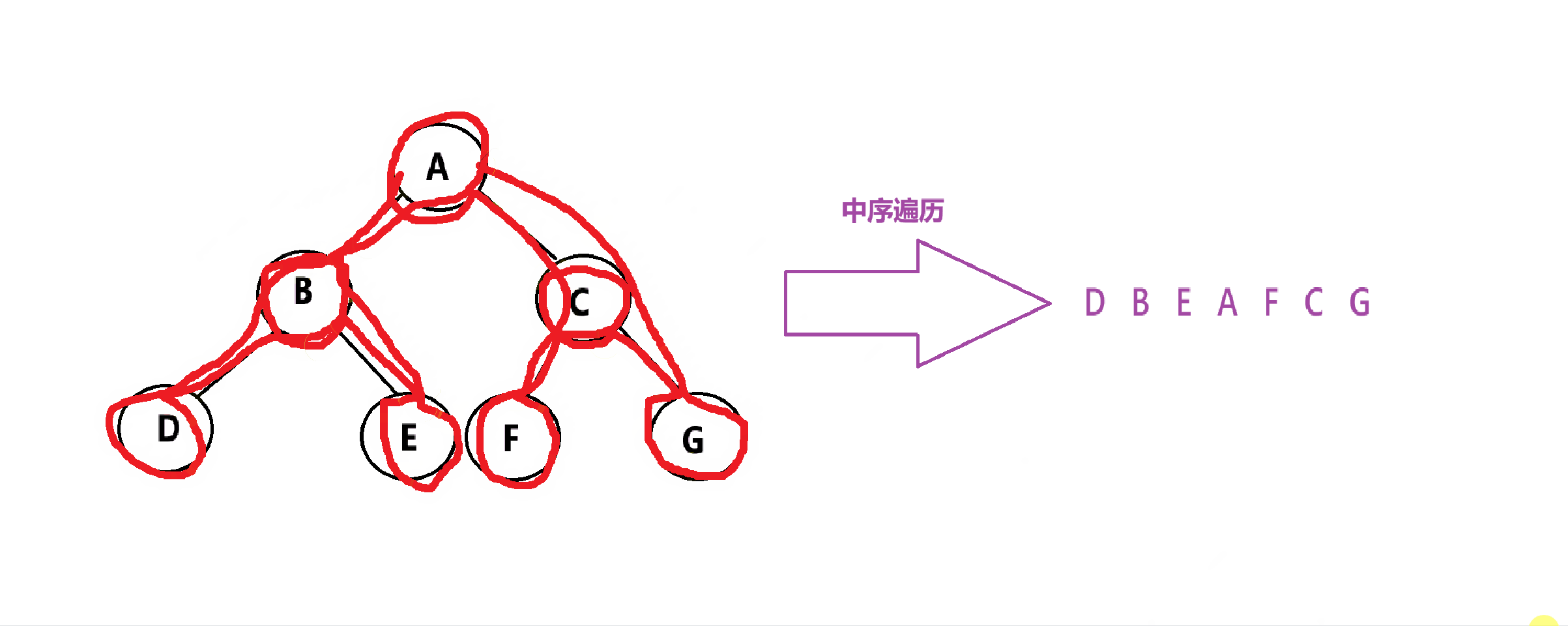
代码实现：

void InOrder(Tree* root)
{if (root == NULL){return;}InOrder(root->left);printf("%d " , root->data);InOrder(root->right);
}

5.2.3、后序遍历

后序遍历：先遍历左子树，再遍历右子树，最后遍历根节点。简称：左右根

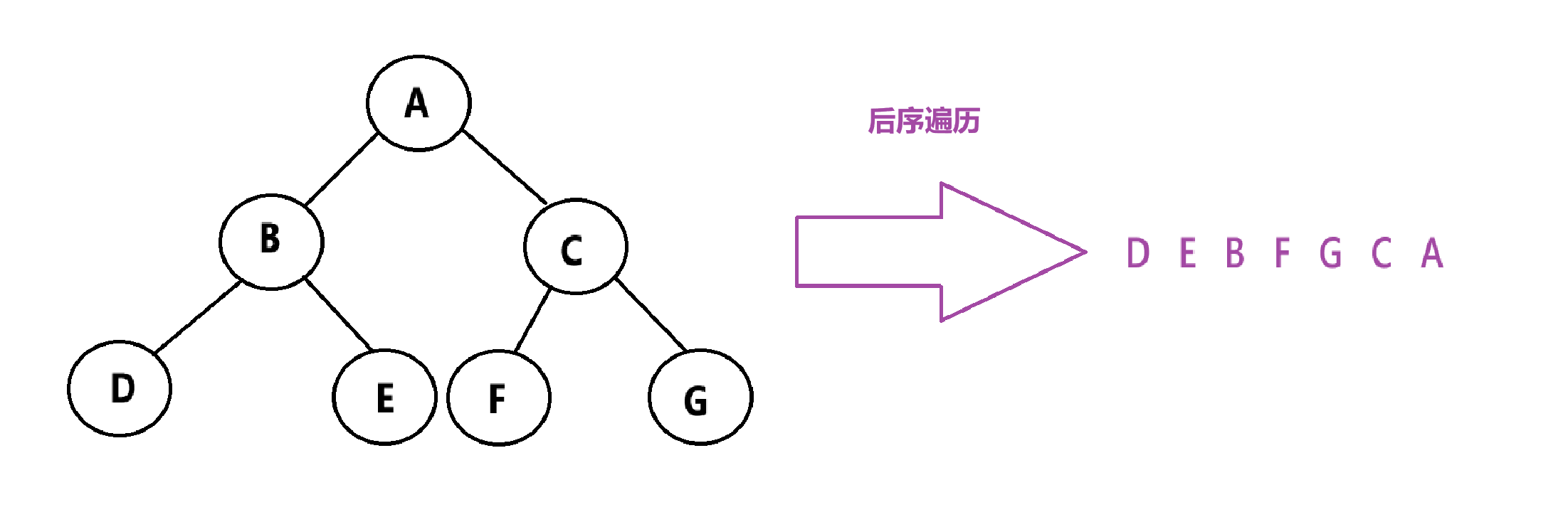
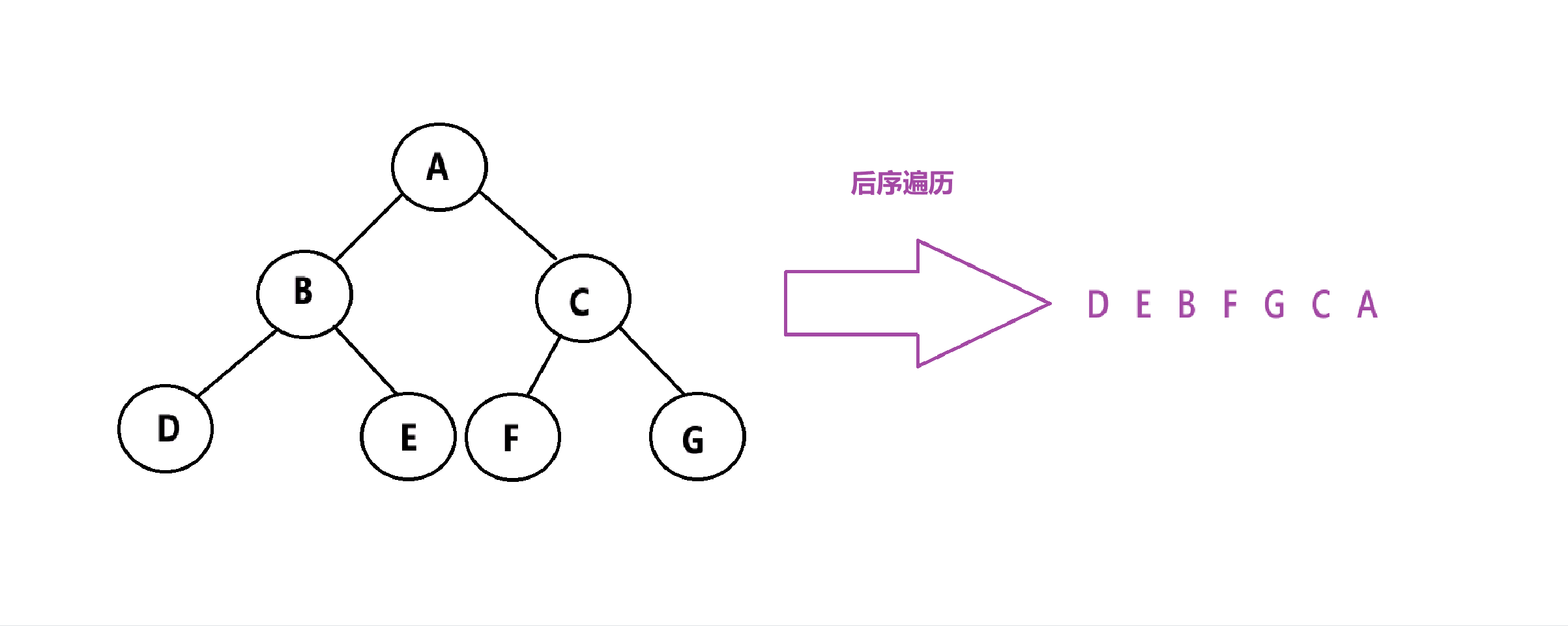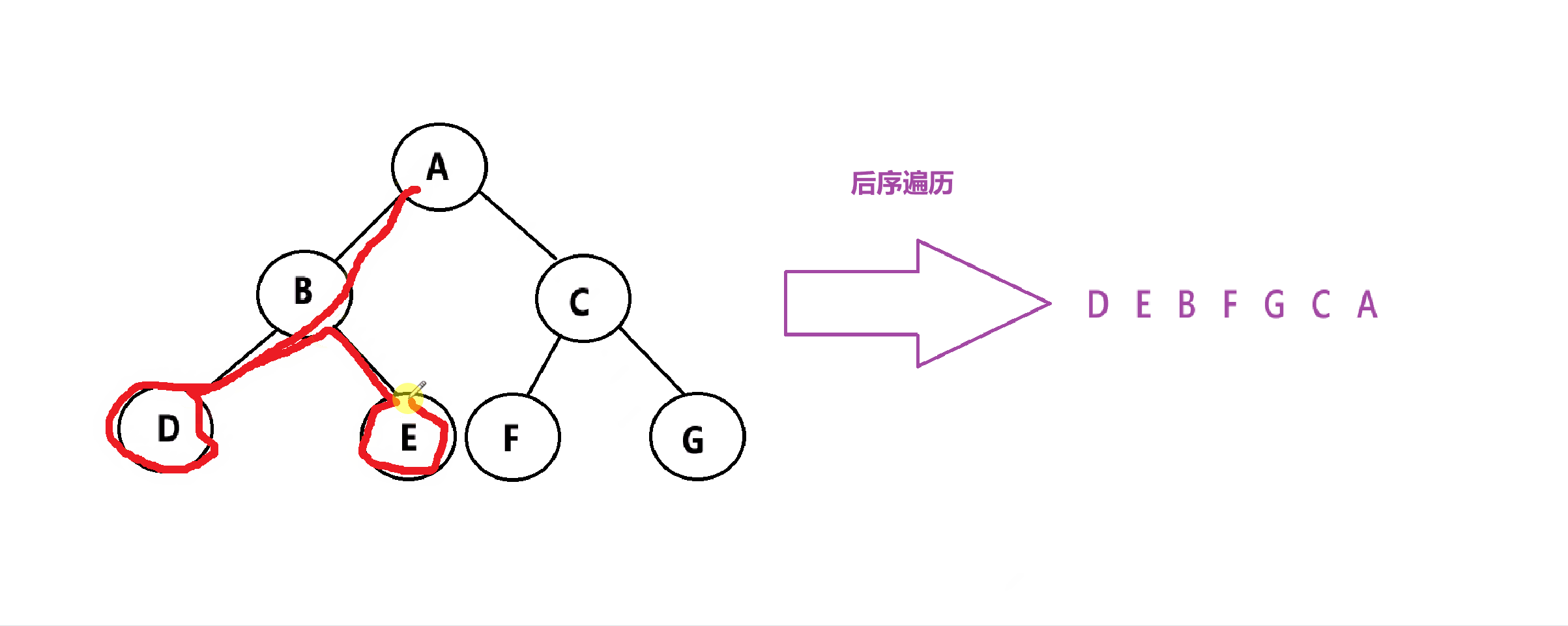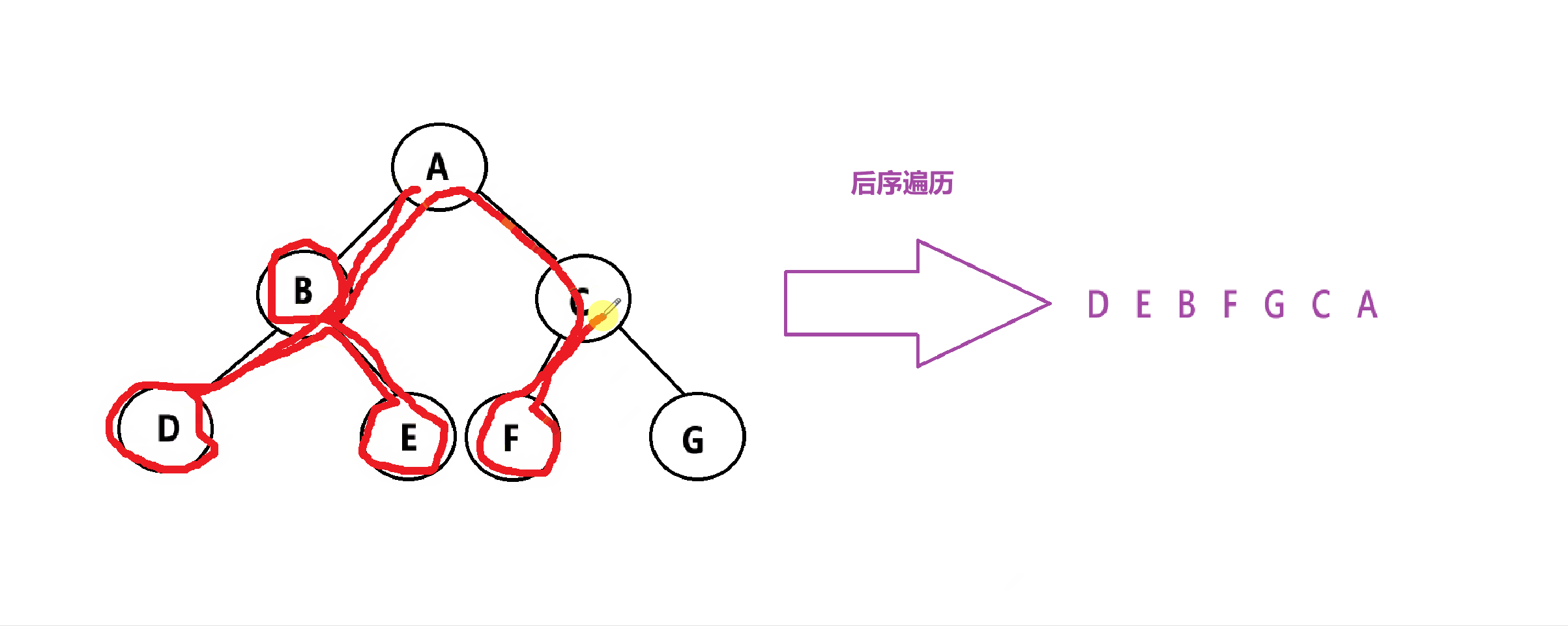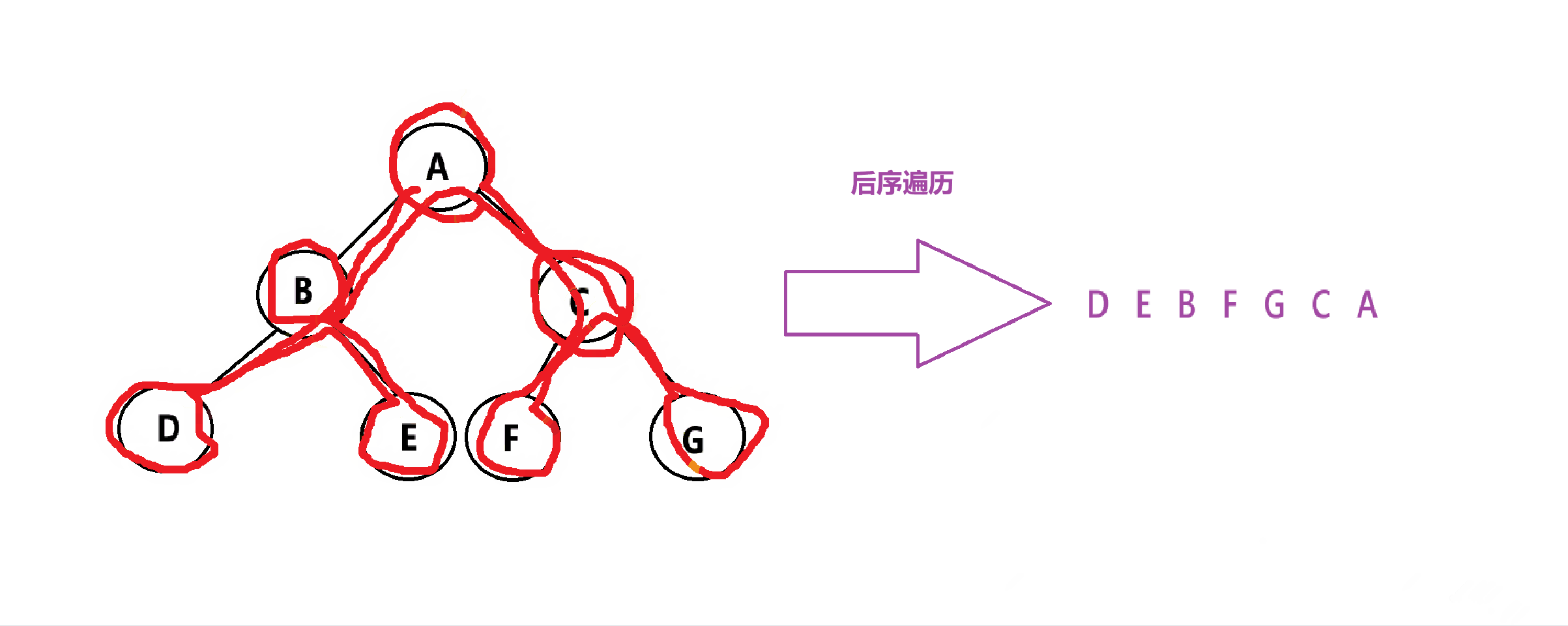
代码实现：

void EndOrder(Tree* root)
{if (root == NULL){return;}EndOrder(root->left);EndOrder(root->right);printf("%d " , root->data);
}

5.2.4、层次遍历

层次遍历：按照层次依次遍历，从左到右，从上到下。

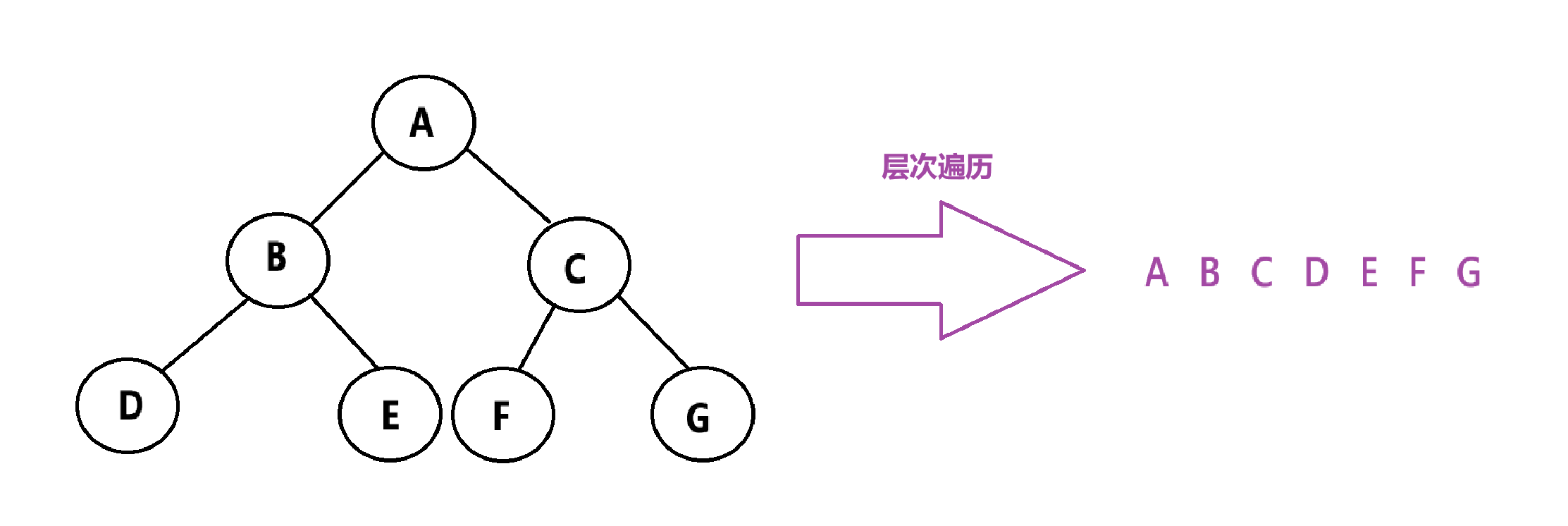
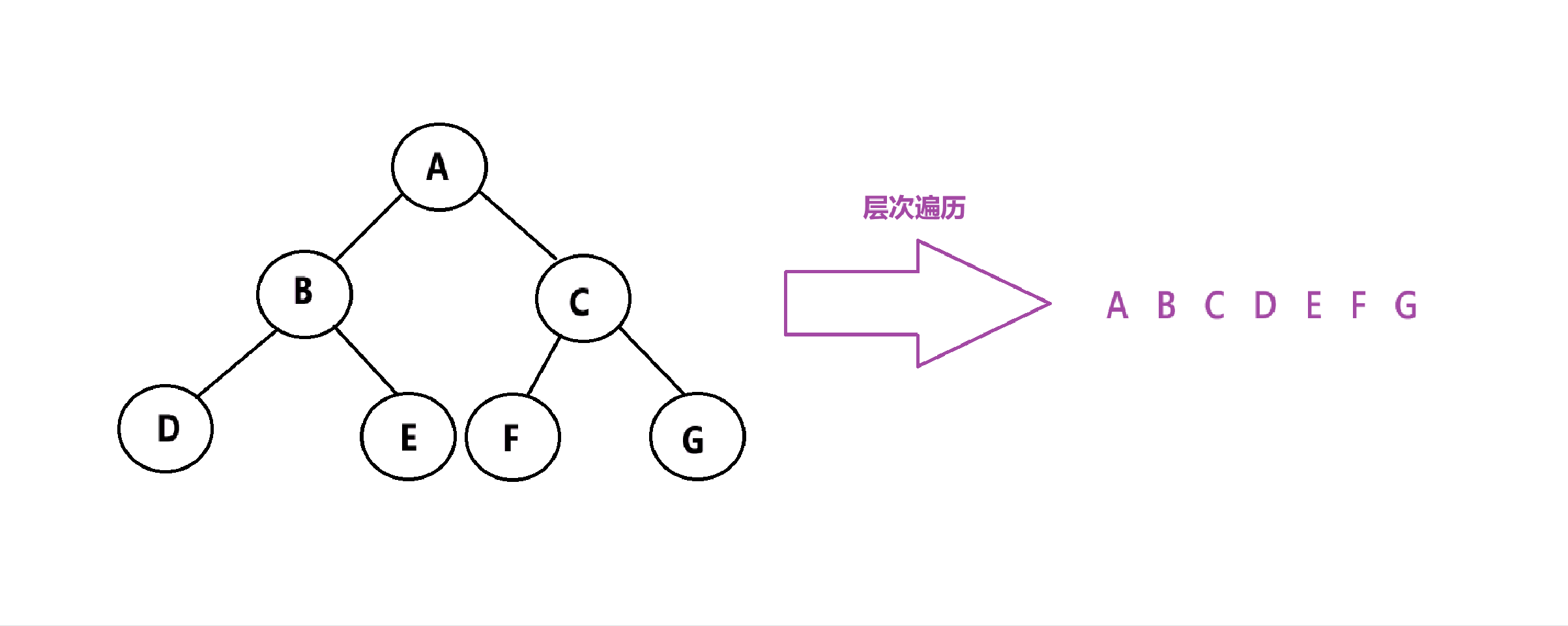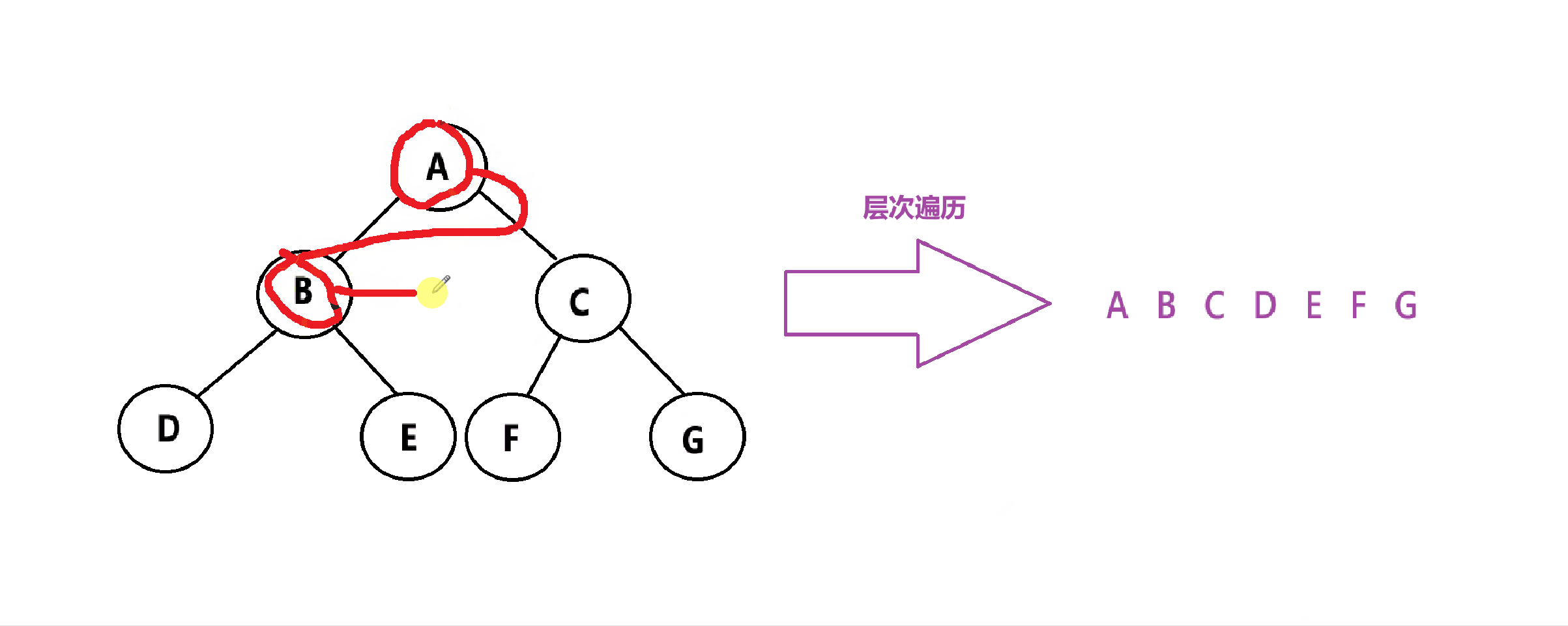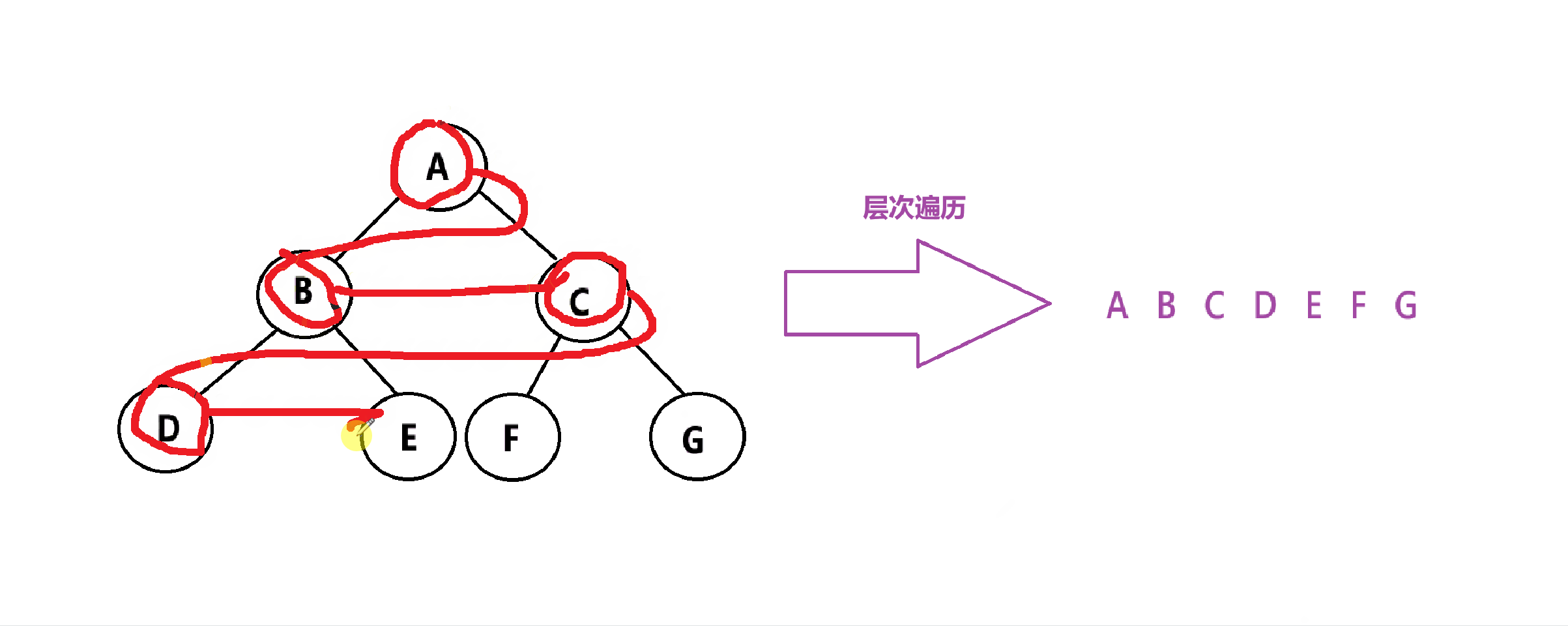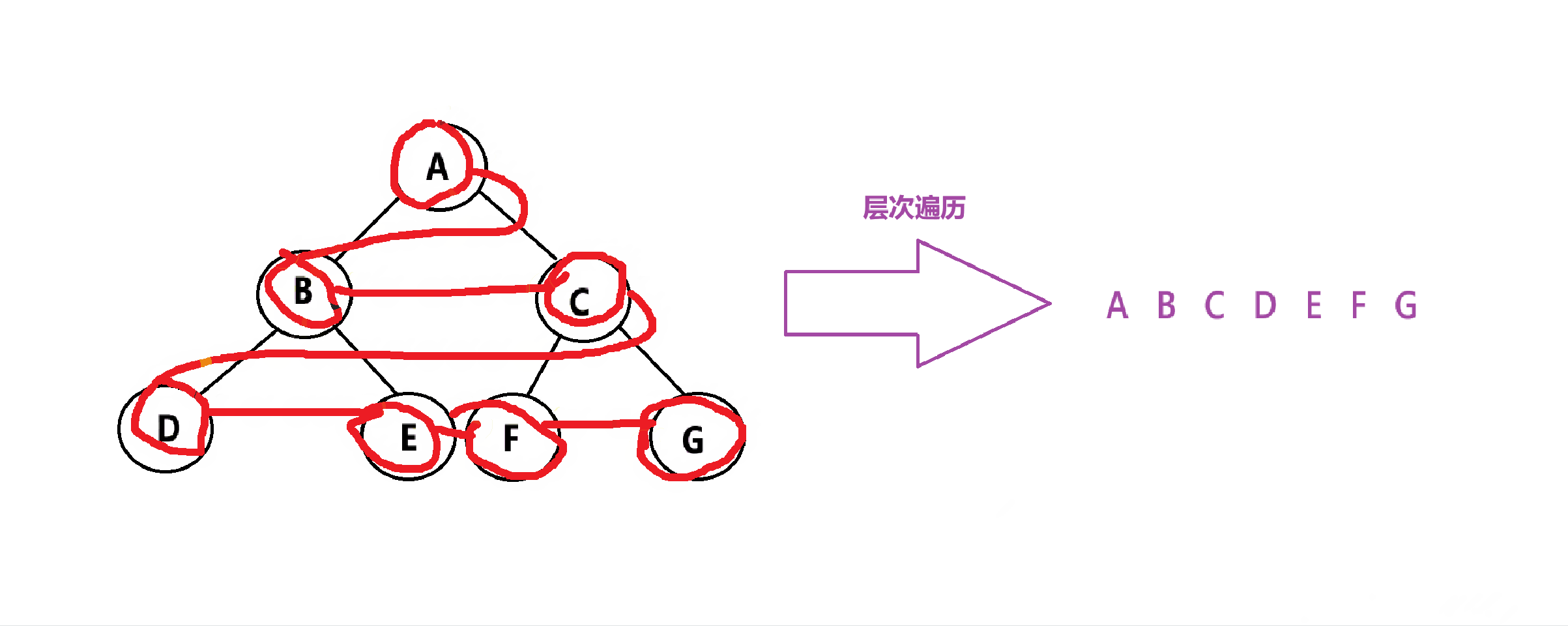
那么，层次遍历该如何实现呢？使用数据结构——队列

步骤如下：

（1）将根节点入队

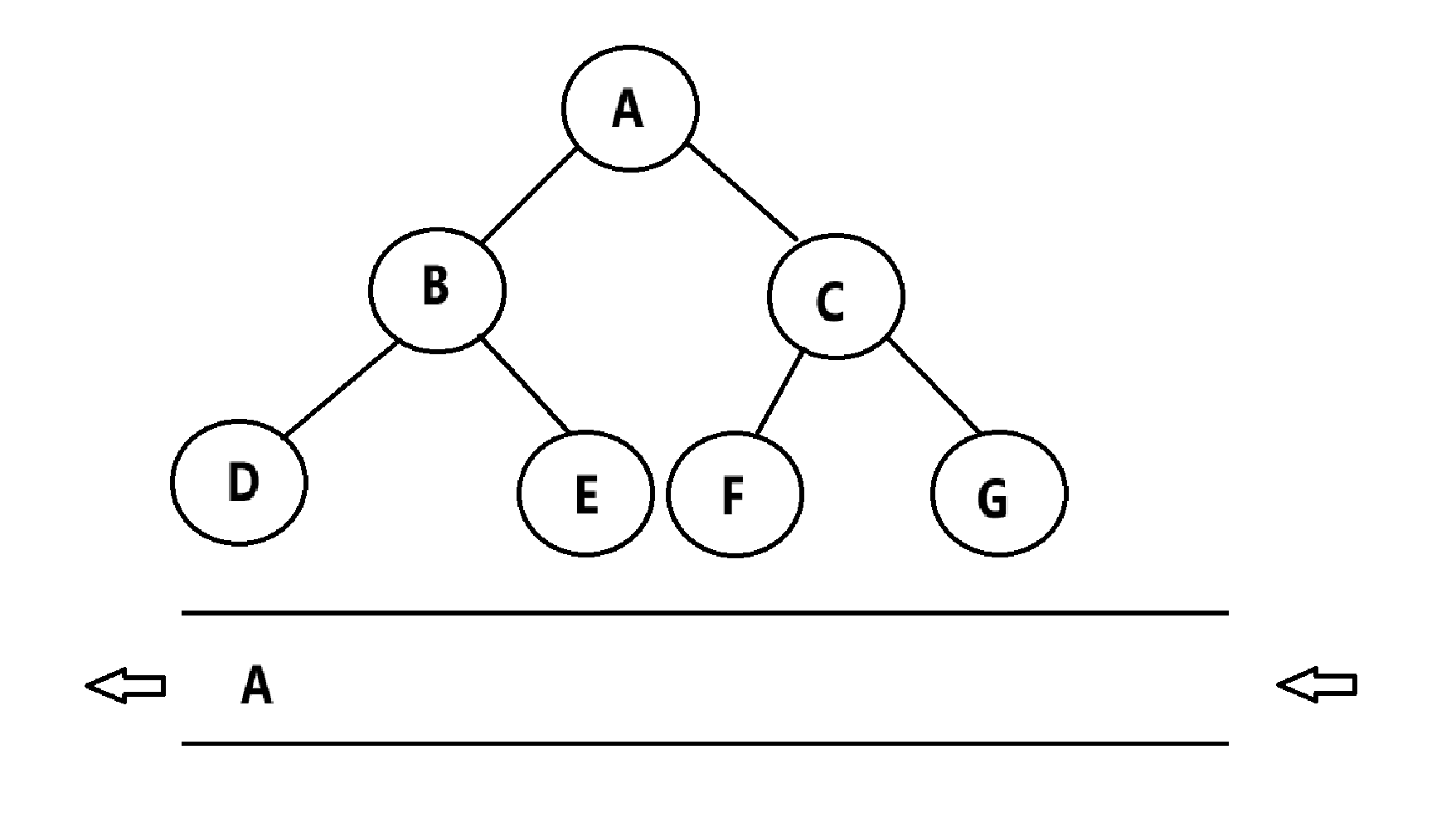
（2）将节点出队，并且让其左右两个孩子入队

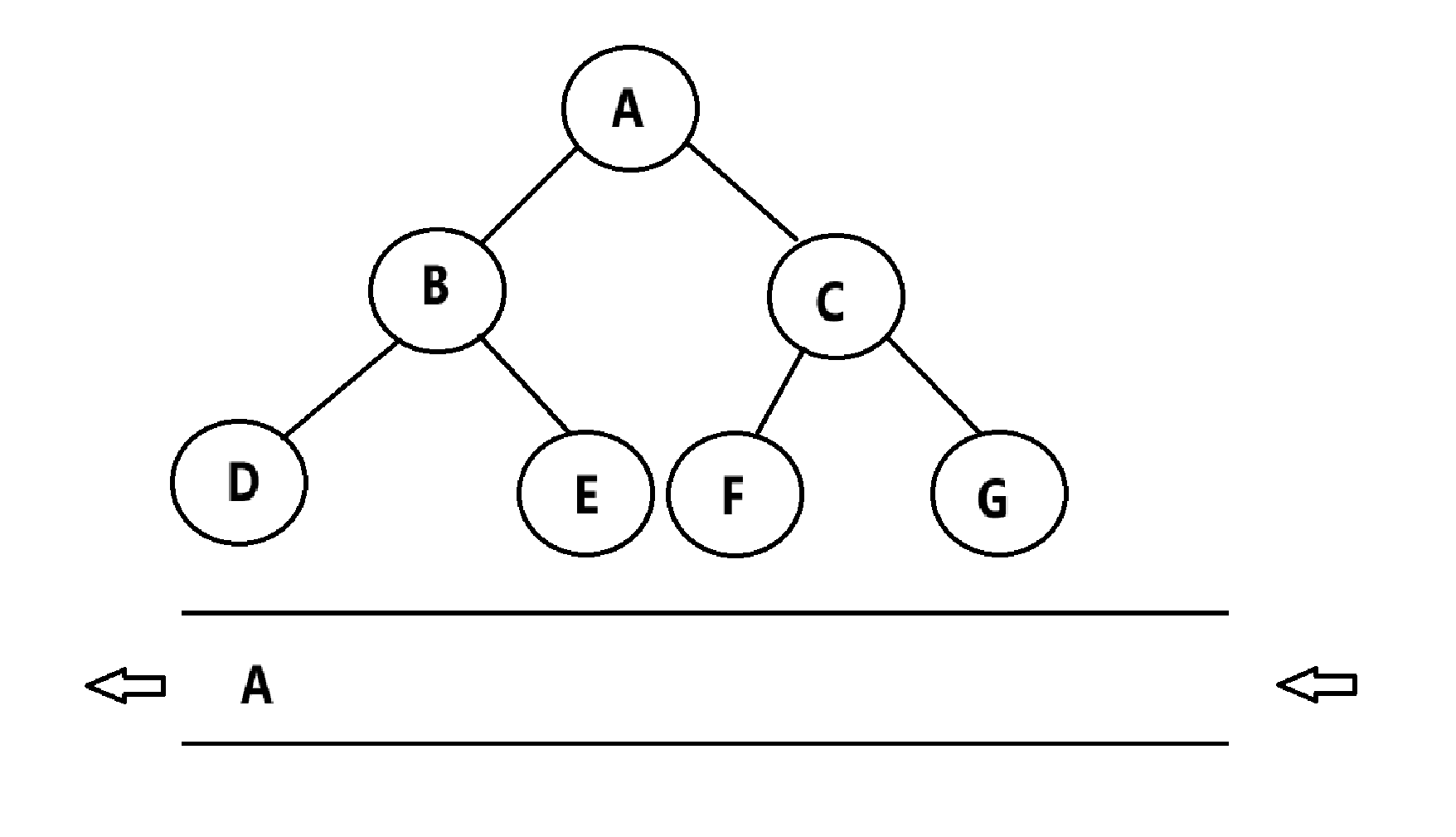
（3）重复步骤（2）的操作，直到队列为空截止

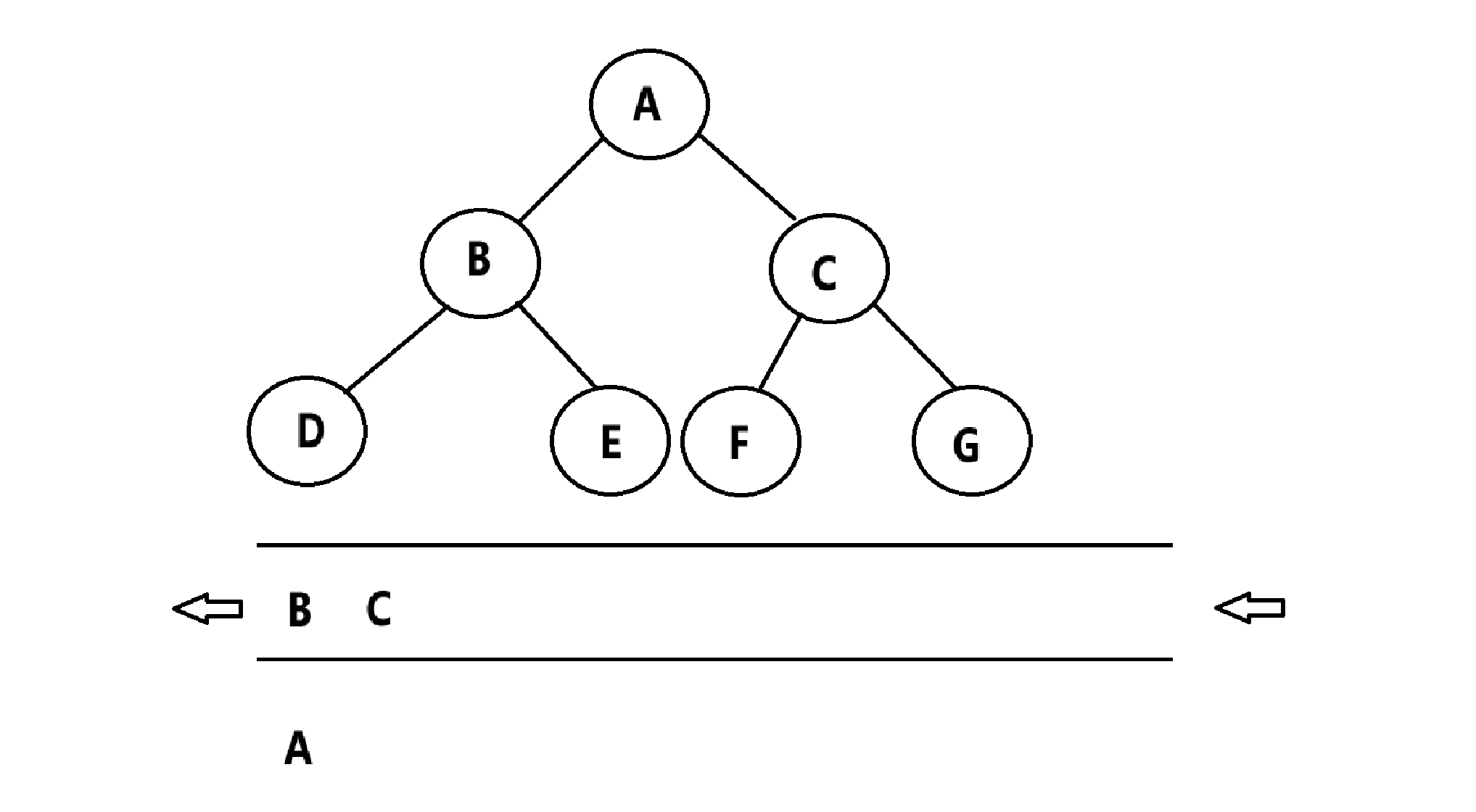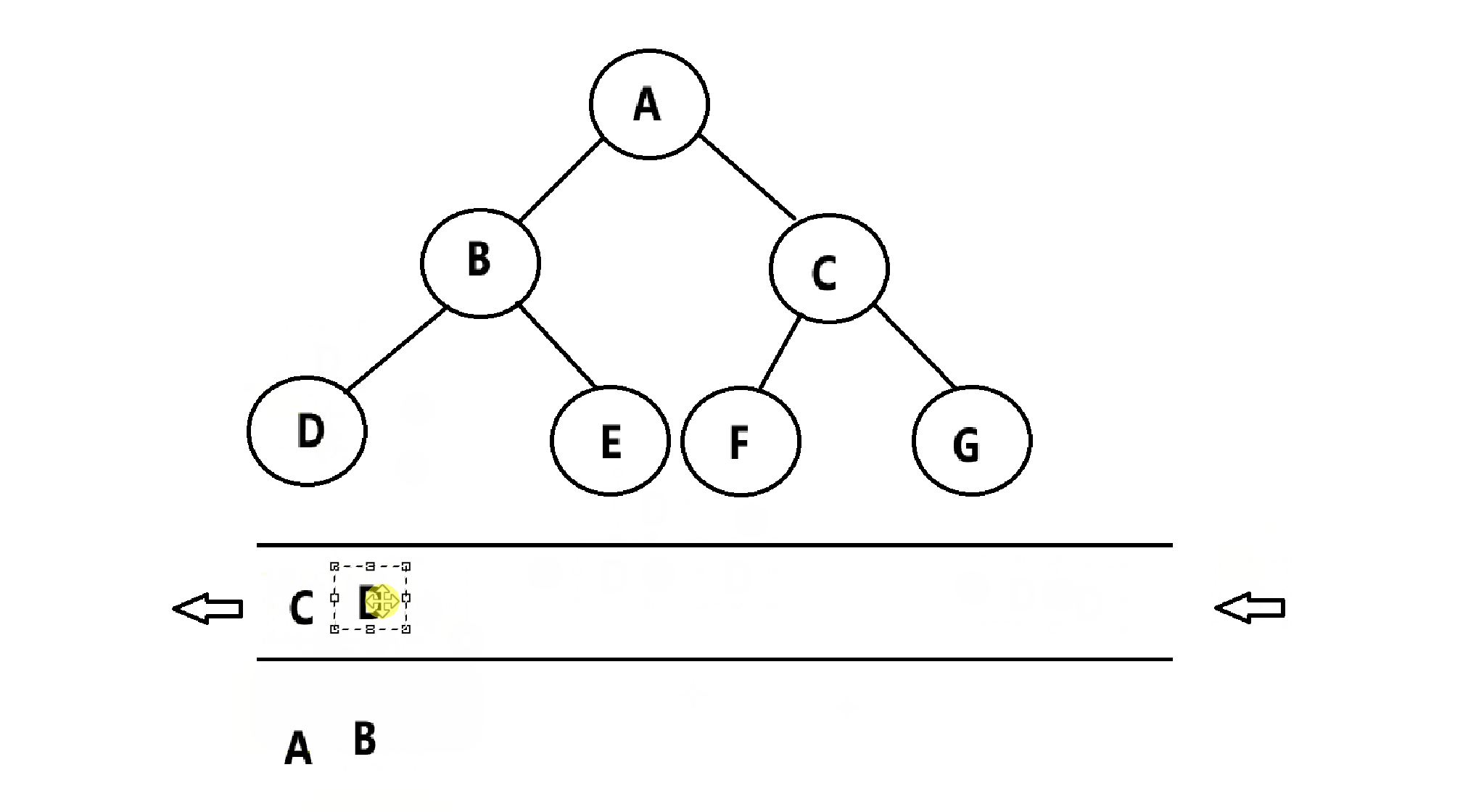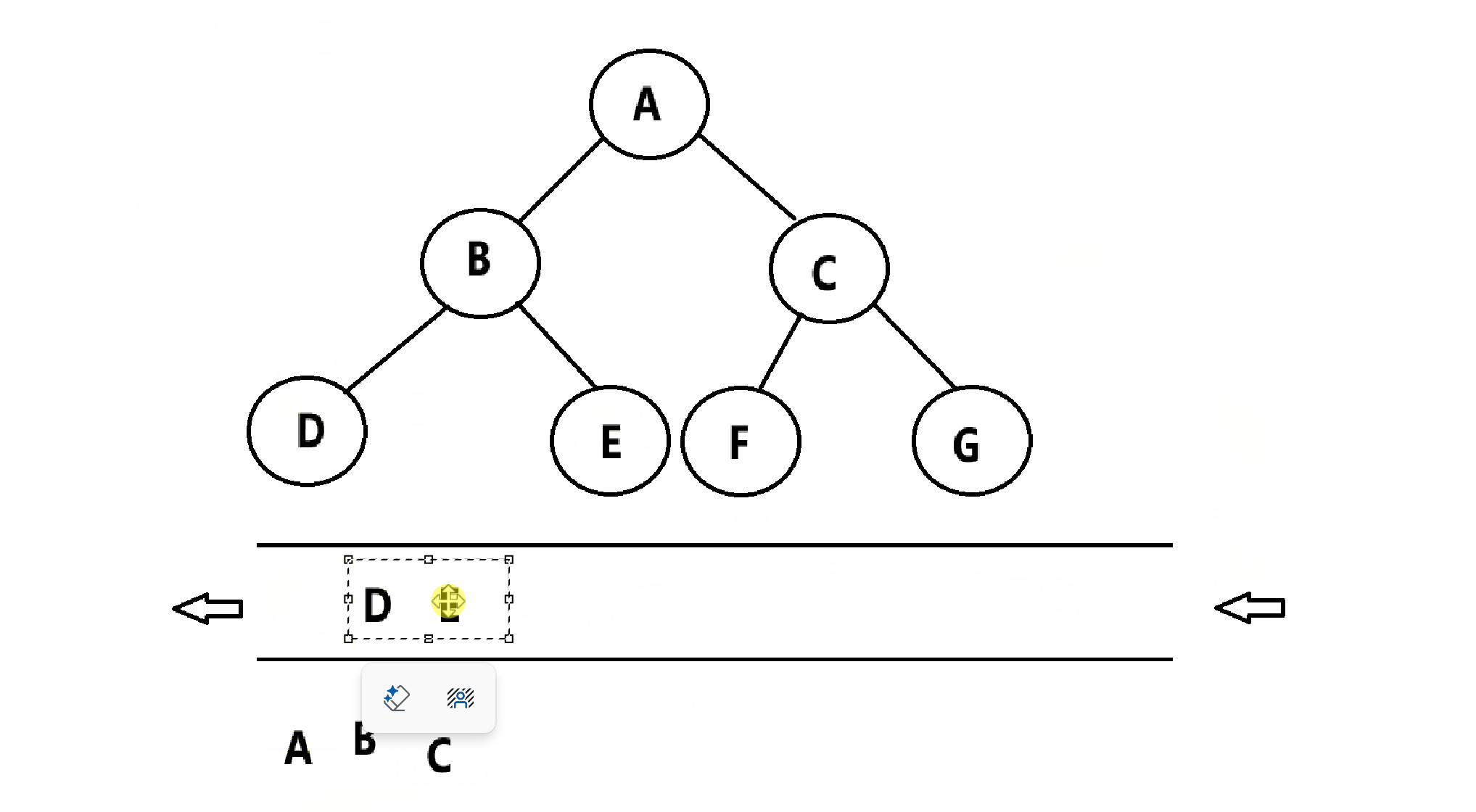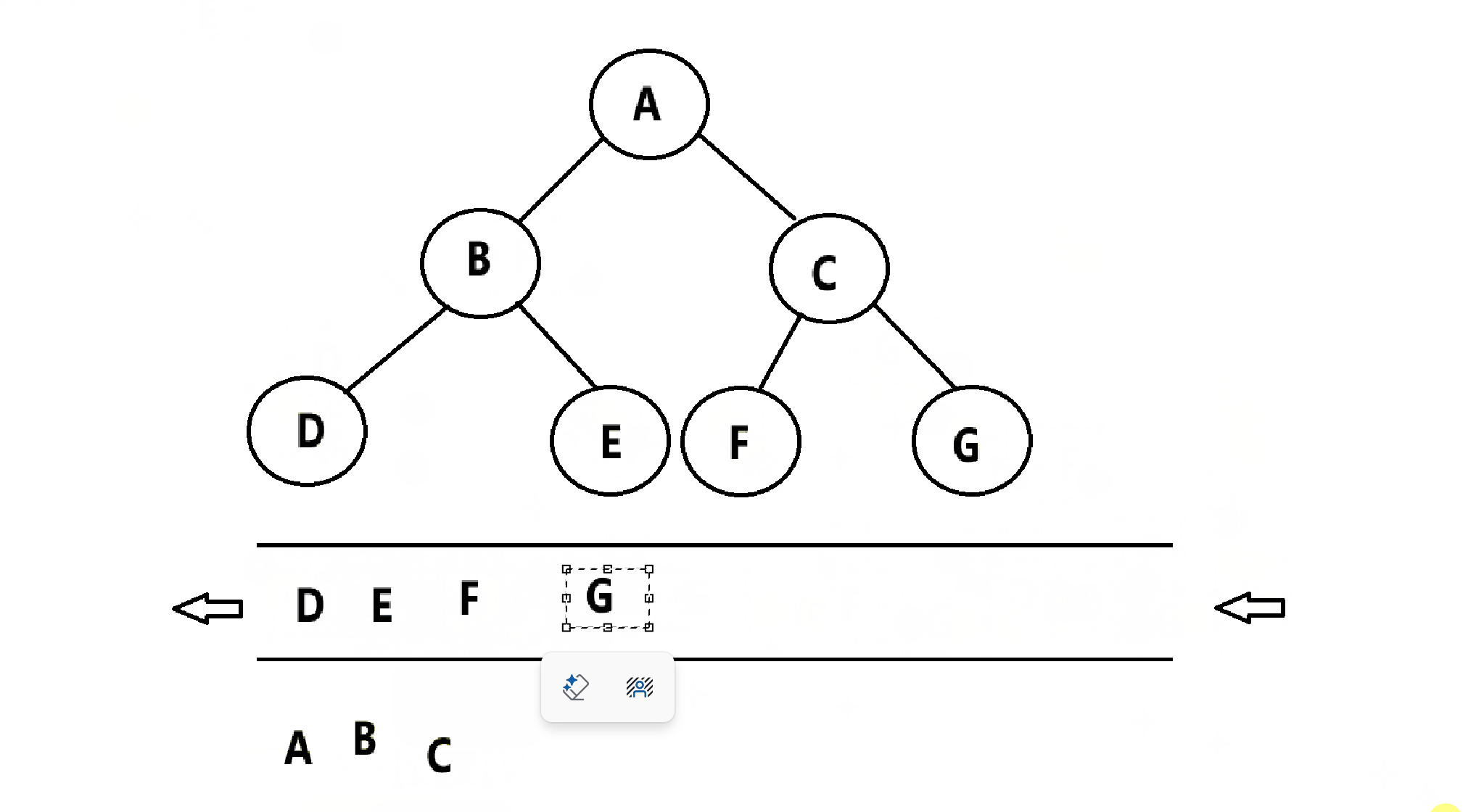
代码实现：（队列相关代码不展现）

void LevelOrder(Tree* root)
{assert(root);//创建一个队列Queue q;QueueInit(&q);//将根节点入队QueuePush(&q, root);//循环出队，左右孩子入队while (!QueueEmpty(&q)){Tree* tmd = QueueTop(&q);QueuePop(&q);if (tmd == NULL)   //叶子结点的左右孩子为NULL，显然NULL不能解引用{continue;}printf("%d " ,tmd->data);QueuePush(&q, tmd->left);QueuePush(&q, tmd->right);}
}

5.3、求二叉树的结点个数

只需要在遍历途中加一个变量num，每次加1就行。但是，如果在函数内部创建变量num，则在递归时，这些num本质上是不同的变量，如果在函数外创建全局变量，那么每次使用完该函数就要手动将num置为0，非常麻烦，那么有没有什么好办法呢？

（1）创建一个函数，在该函数中创建一个变量num，并置为0，然后调用遍历递归函数。

（2）使用层序遍历，因为层序遍历是非递归的

（3）使用递归，不创建临时变量，直接返回一个数字

由于（1）（2）非常简单，但是不常用，所以我们着重看第三个。

总节点数 = 1+左子树结点数+右子树结点数，所以我们的返回值就返回这个。

int TreeSize(Tree* root)
{if (root == NULL){return 0;}else{return 1 + TreeSize(root->left) + TreeSize(root->right);}
}

5.4、求二叉树叶子结点的个数

与求结点总数同理，叶子结点个数可以拆成左子树叶子节点个数+右子树叶子节点个数。

代码如下：

int TreeLeafSize(Tree* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

5.5、求二叉树第 k 层的结点个数

同样的的道理，第 k 层节点的个数等于左子树第 k 层的节点个数+右子树第 k 层节点个数。但是，如何辨别是否为第 k 层节点呢？

在函数的参数设计时加上一个参数 k，每次递归调用时 k-1即可。

int TreeLevelSize(Tree* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return TreeLevelSize(root->left, k - 1) + TreeLevelSize(root->right, k - 1);
}

5.6、求二叉树的深度

所以递归的返回值取最大值就好了。

int TreeDepth(Tree* root)
{if (root == NULL){return 0;}int leftdepth = TreeDepth(root->left);int rightdepth = TreeDepth(root->right);return 1 + (leftdepth > rightdepth ? leftdepth : rightdepth);
}

5.7、查找二叉树特定值的结点

还是一样，在遍历递归中寻找特定值

Tree* TreeFind(Tree* root, TreeDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}Tree* leftfind = TreeFind(root->left, x);if (leftfind){return leftfind;}Tree* rightfind = TreeFind(root->right, x);if (rightfind){return rightfind;}if (leftfind == NULL && rightfind == NULL){return NULL;}
}

节点值不匹配就返回NULL，匹配就返回该节点。为了使某个节点能一级一级函数返回到最后一层函数，就需要加上条件语句，判断是不是非NULL。

5.8、二叉树的销毁

需要一个节点一个节点销毁，可以选择递归销毁，也可以选择借助队列销毁。这里选择递归销毁。

void TreeDestory(Tree** root)
{if (*root == NULL){return;}Tree* left = (*root)->left;Tree* right = (*root)->right;free(*root);*root = NULL;TreeDestory(&left);TreeDestory(&right);
}

5.9、判断二叉树是不是完全二叉树

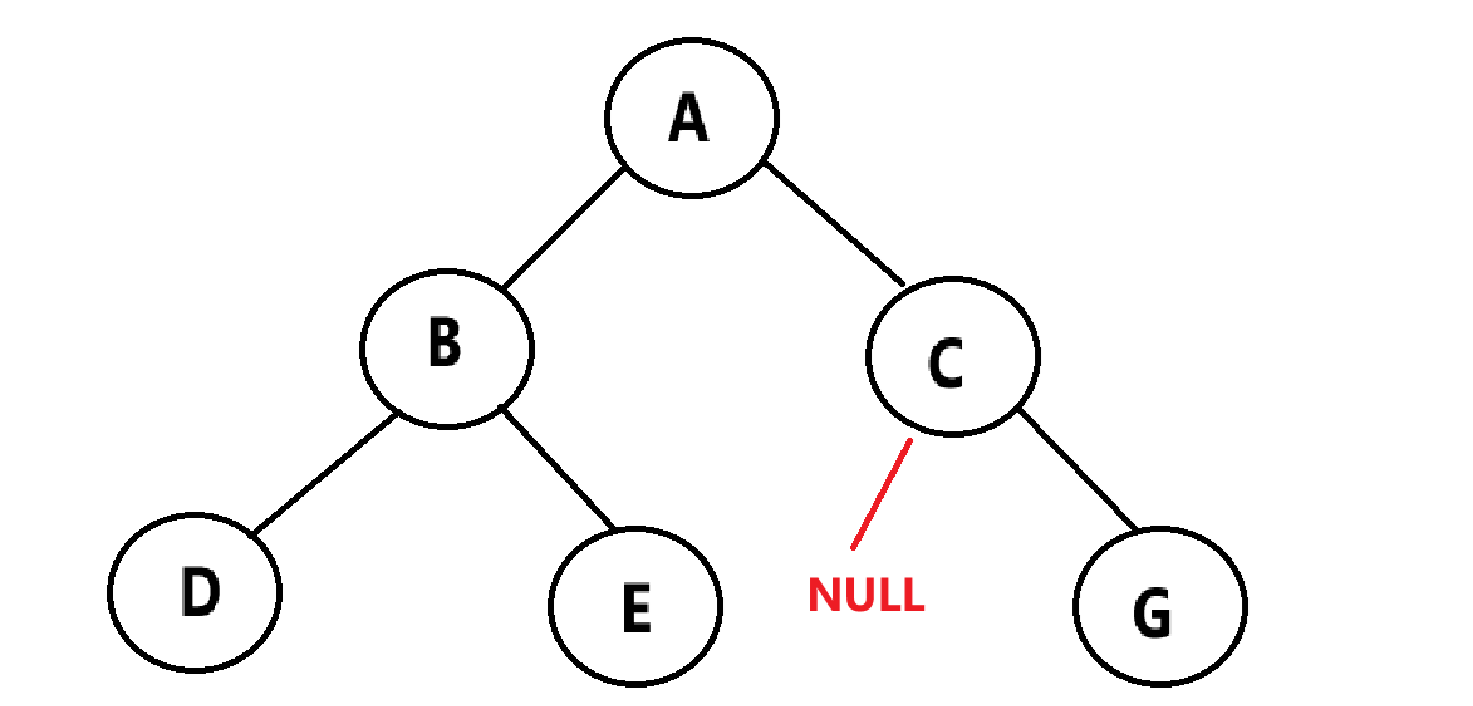
如图，不是一个完全二叉树，可以看到，如果没有 G节点，该棵树还是完全二叉树。所以，判断一颗树是不是二叉树可以层次遍历，在第一个NULL出现后，还有没有非NULL节点，如果还有，则证明不是完全二叉树。

bool TreeComplete(Tree* root)
{assert(root);//进行层次遍历Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){Tree* tmd = QueueTop(&q);QueuePop(&q);if (tmd == NULL){//层次遍历遇见第一个NULL跳出循环，查看后面还有没有非NULL节点break;}QueuePush(&q, tmd->left);QueuePush(&q, tmd->right);}//查看有没有非NULL节点while (!QueueEmpty(&q)){Tree* tmd = QueueTop(&q);QueuePop(&q);if (tmd != NULL){QueueDestory(&q);return false;}}QueueDestory(&q);return true;
}

六、练习题

6.1、单值二叉树

965. 单值二叉树 - 力扣（LeetCode）

要判断是否为单值二叉树，可以遍历二叉树，在遍历的途中检查节点数值是否相同。怎么比较合适呢？当然是孩子和父母比合适（兄弟之间比较中间还要隔一个父母，麻烦）

bool isUnivalTree(struct TreeNode* root) {if(root == NULL){return true;   }if(root->left && root->left->val != root->val){return false;}if(root->right && root->right->val != root->val){return false;}return isUnivalTree(root->left) && isUnivalTree(root->right);
}

6.2、检查两颗二叉树是否相同

100. 相同的树 - 力扣（LeetCode）

首先，要判断两个二叉树的结构是否相同，然后再判断值是否相同。也就是只有两个节点都不为NULL才能判断值。

typedef struct TreeNode TreeNode;
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if( p == NULL && q == NULL){return true;}if( p == NULL || q == NULL){return false;}//比较节点值if( p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right ,q->right);
}

这里要注意一下，最后判断两个节点值是否相同时，不能用else返回true 。原因是：如果else反悔了true，那么两个节点的所有情况都会有返回值，最后代码的递归调用部分将永远无法执行。

其次，为什么只判断值不相等返回false而不是判断值相等返回false呢？原因是：只要有一个节点返回的false，那么后面的且运算就不执行了。换句话说，是题目的意思的逻辑关系造就了最后必须是挑出错误的选项，然后返回，使用逻辑且连接左右子树的返回值。举个简单的例子：如果只找条件相等的返回true，那么false只能通过二叉树的结构不同得到，节点值不相同得不到false，这也与题目相违背。还有最后的左右子树结果的逻辑且，如果换成逻辑或，那么最后的答案必定是true，这也不对。

6.3、对称二叉树

101. 对称二叉树 - 力扣（LeetCode）

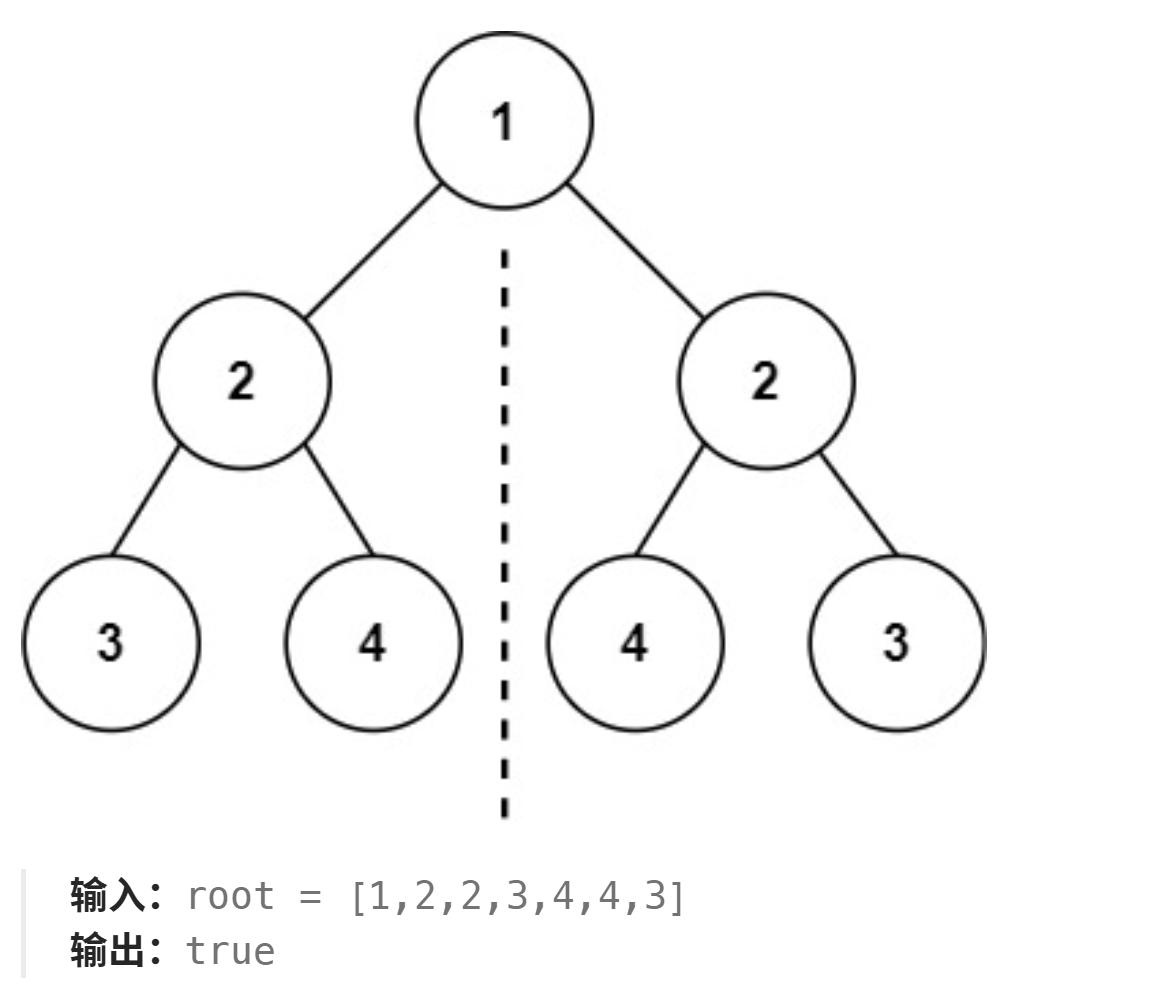
在弄懂了上一道题相同的二叉树后，这道题就简单多了。上一道题是比较两个位置相同的结点，这道题则是比较位置对称的结点，我们只需要稍微改动一下代码就可以了，比如，递归调用的时候，第一个参数传左孩子，第二个参数传右孩子。

typedef struct TreeNode TreeNode;
bool isSameTree(TreeNode* q , TreeNode* p)
{if( q == NULL && p == NULL){return true;}if( q == NULL || p == NULL){return false;}if( q->val != p->val){return false;}return isSameTree(q->left , p->right) && isSameTree(q->right , p->left);
}
bool isSymmetric(struct TreeNode* root) {return isSameTree(root->left, root->right);
}

6.4、另一棵树的子树

572. 另一棵树的子树 - 力扣（LeetCode）

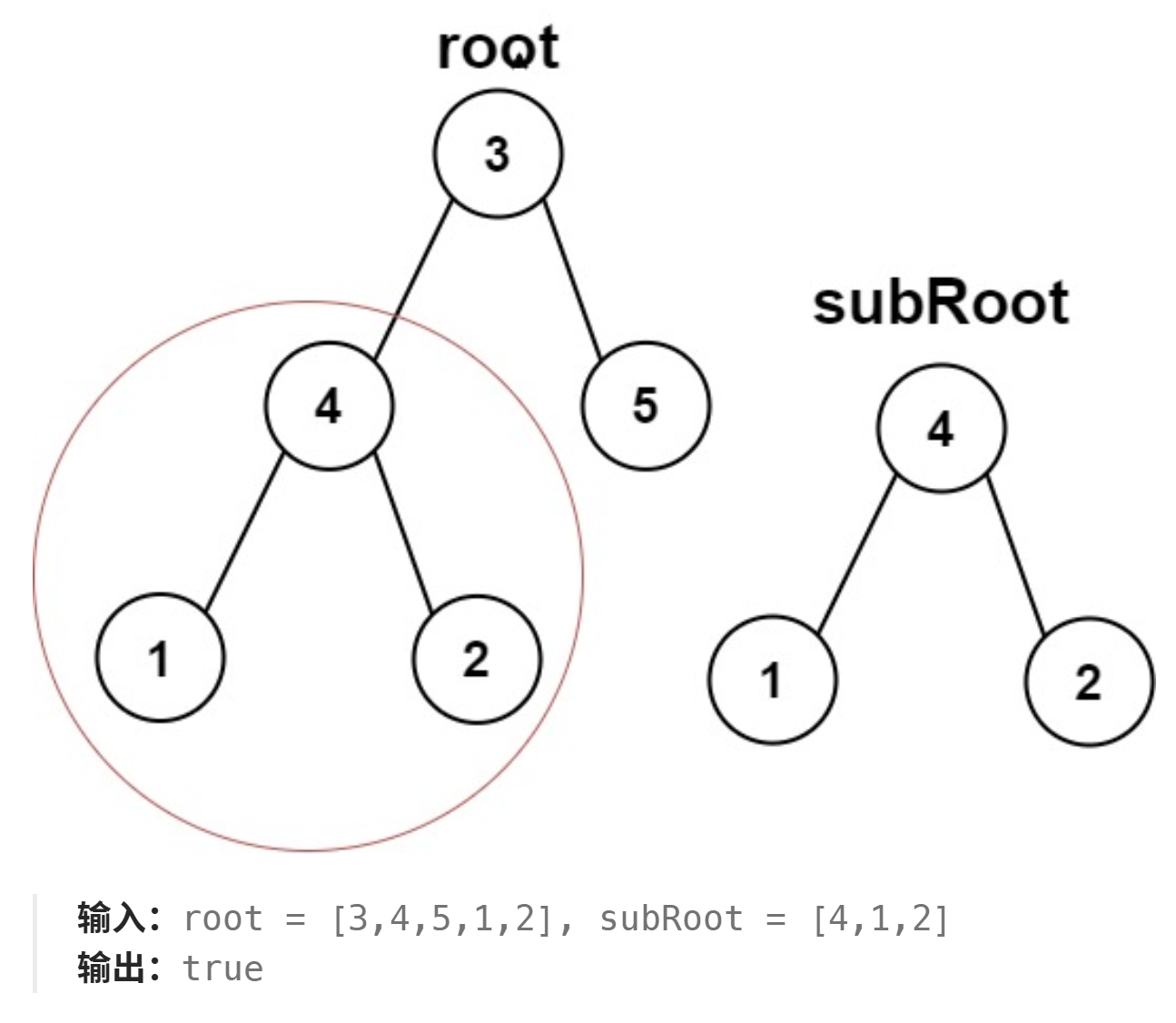
只需要判断每个子树是否相同即可

typedef struct TreeNode TreeNode;
bool isSameTree(TreeNode* q , TreeNode* p)
{if( q == NULL && p == NULL){return true;}if( q == NULL || p == NULL){return false;}if( q->val != p->val){return false;}return isSameTree(q->left,p->left) && isSameTree(q->right,p->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {if( root == NULL){return false;}if(isSameTree(root, subRoot)){return true;}return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

6.5、二叉树的遍历

二叉树遍历_牛客题霸_牛客网

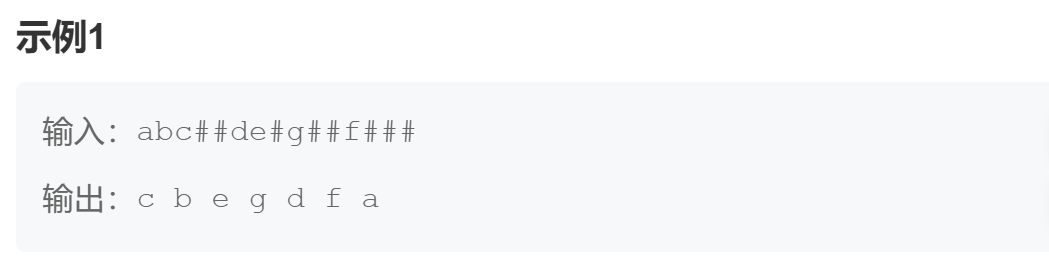
根据实例知道，给你一个先序遍历，让你给出中序遍历的结果。按理来说，只给一个先序遍历是不能确定树的结构的，但是这道题给的先序遍历中出现了 '#'，也就是NULL，那么树的结构就可以确立了。

这道题只看构建树的部分。

首先，该函数一定得是个递归函数，没错吧？其次，还要有递归结束的点（NULL），最后，还要把数据放入各个节点中。

那么，我们如何知道该放那个数据呢？所以函数的参数要引入一个参考 pi ，而且 pi 还必须随着函数的递归调用而修改，所以还是个传址的参数。

TreeNode* BinaryTreeCreat(TreeDataType* arr ,int* pi)
{if( arr[*pi] == '#'){(*pi)++;return NULL;}//创建新节点TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));if( root == NULL){perror("malloc fail!");exit(1);}//按照先序遍历的顺序进行root->val = arr[(*pi)++];root->left = BinaryTreeCreat(arr ,pi);root->right = BinaryTreeCreat(arr ,pi);return root;
}

这里不管什么顺序的遍历，都必须先创建一个空节点，否则，左右孩子怎么来？

6.6、根据两种已知遍历，求树的结构

已知某二叉树的中序遍历序列为JGDHKBAELIMCF，后序遍历序列为JGKHDBLMIEFCA，则其前序遍历序列为？

中序遍历：左根右；

后序遍历：左右根。

后序遍历最后一个遍历的，必定是根节点，所以这颗树的根节点为 A 。而中序遍历，A的左边为左子树，右边为右子树。

如图：先在后序遍历中删掉根节点 A ,然后去中序遍历找到 A。接着，在后序遍历中找到最后一个元素C，再在中序遍历中找到C。发现C在A的右边，所以C是A的右子树。

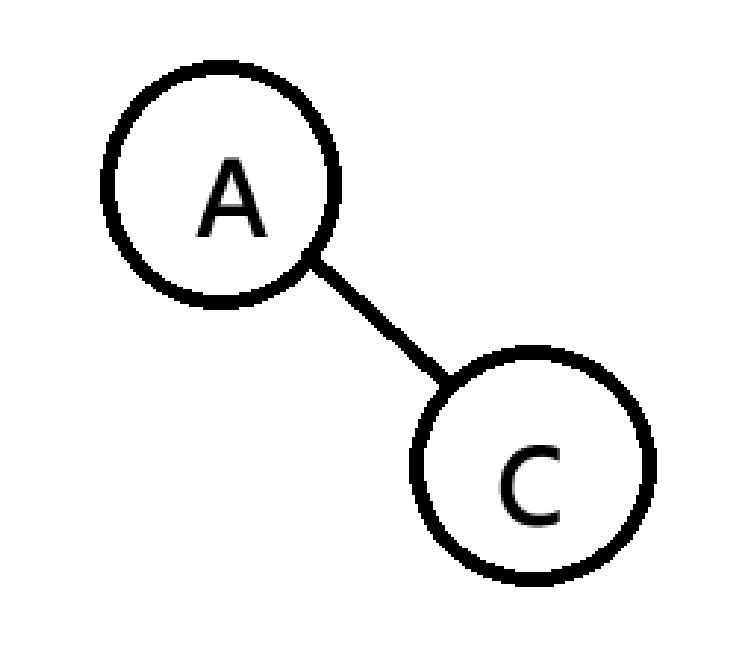
然后再在中序遍历中找F，看看F关于C的位置，以此类推，最后的先序遍历为：ABDGJHKCEILMF。

注意：为什么这种方法能用？因为有中序遍历，后序遍历第一次提供一个根节点，这个根节点在中序遍历中可以将子树一分为二，左边为左子树里的节点，右边为右子树里的节点；而后序遍历删掉根节点后，最后一个元素为剩下左右子树的根节点其中之一，再根据它在中序遍历里的位置，就可以判断到底应该是左孩子还是右孩子。而如果只有先序遍历和后序遍历，无法区分到底在左边还是右边，因此，给定两个遍历序列，必须要有一个为中序遍历，才能有唯一的解。