鞍点(Saddle Point)一文通透从曲面直觉到博弈与优化
1. 先用画面建立直觉
想象一个马鞍:沿着马背方向是凹(往下),沿着左右方向是凸(往上)。经典函数
z=x2−y2 z = x^2 - y^2 z=x2−y2
在原点 (0,0)(0,0)(0,0) 的形状就像马鞍——这就是“鞍点”。它既不是最高点也不是最低点:顺着 xxx 轴往外走会升高(像上坡),顺着 yyy 轴往外走会降低(像下坡)。
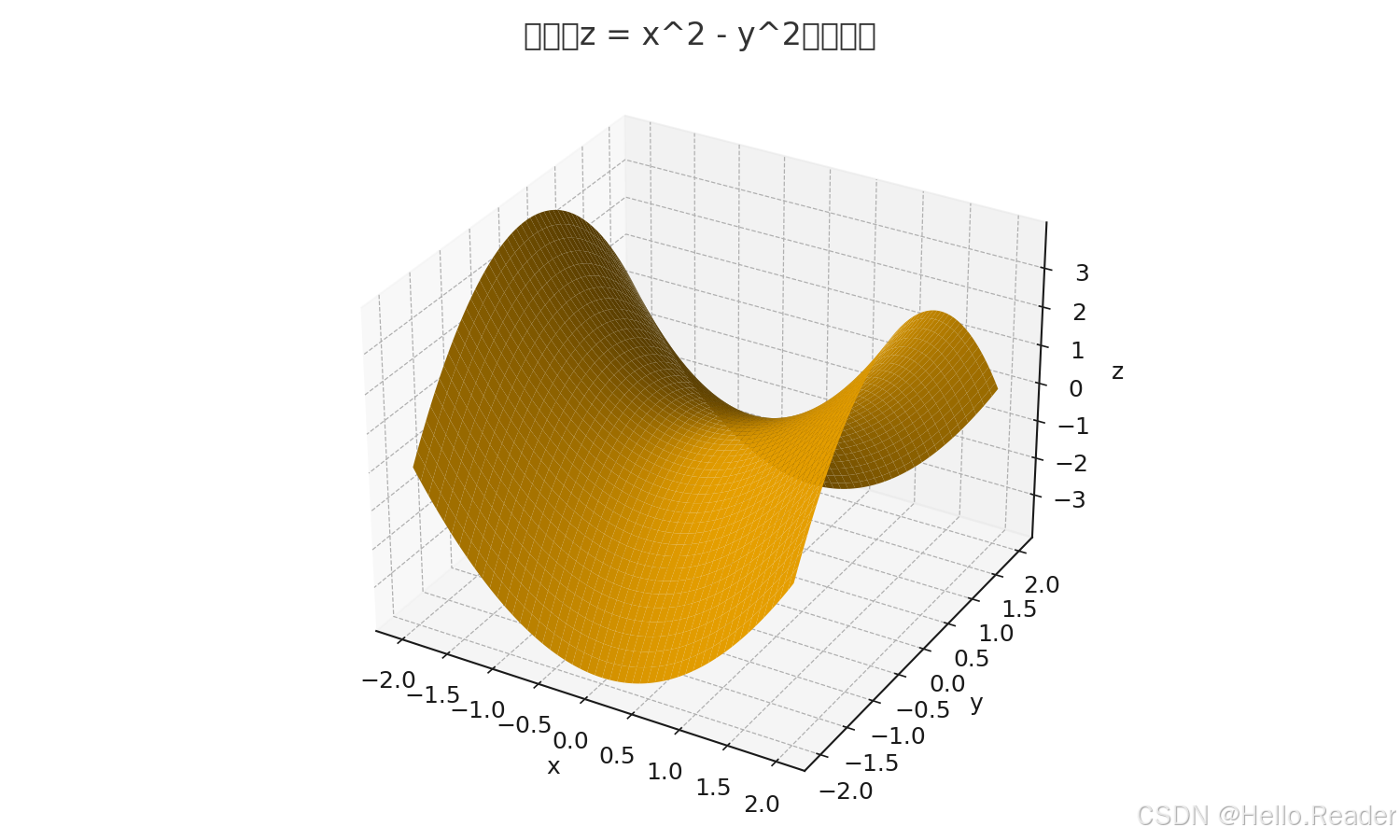
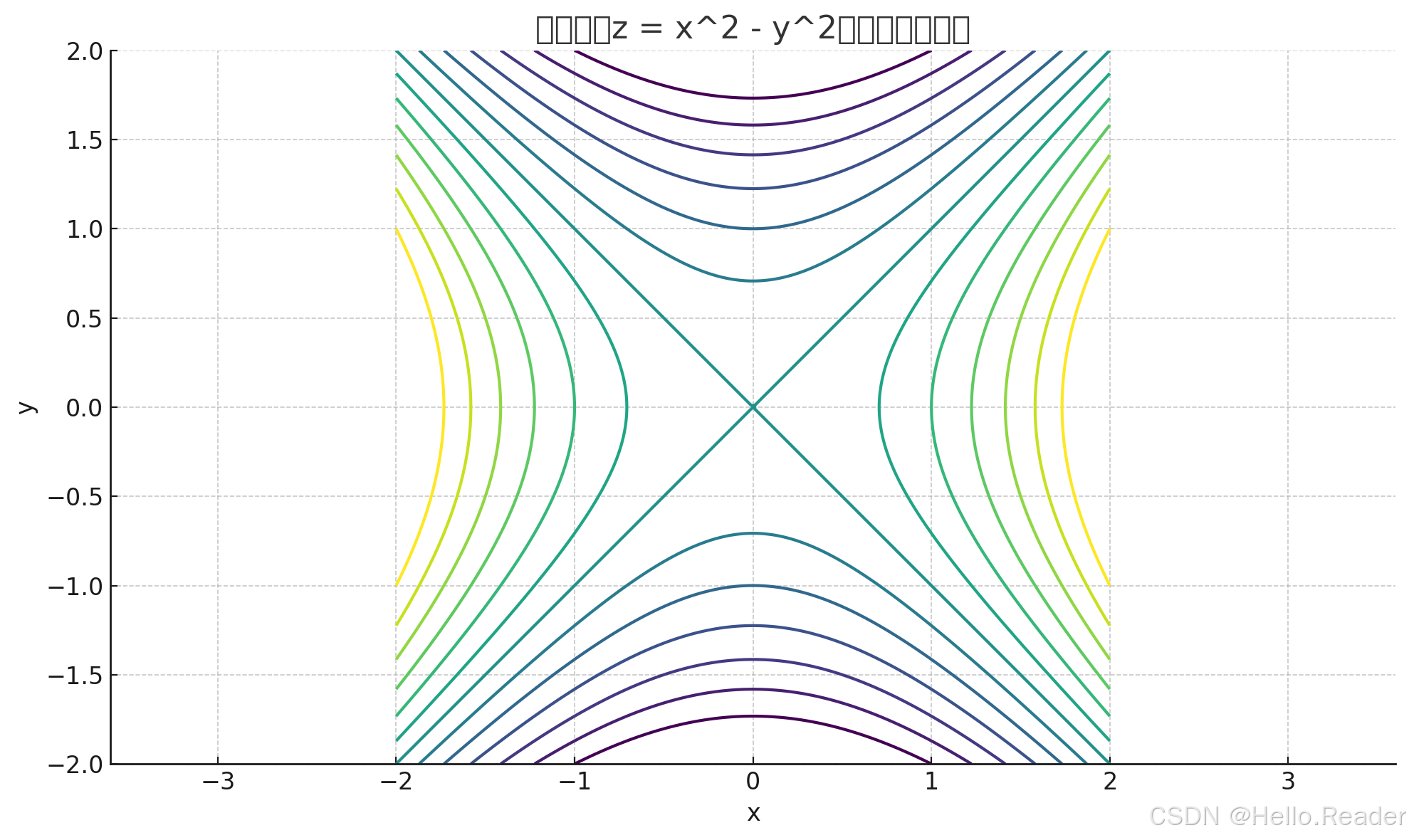
上面两张图直观展示了这一点:一张是三维曲面,一张是等高线(原点附近呈“X”形的等高线交错)。
2. 三类“鞍点”,别混了
2.1 多元函数里的鞍点(微积分/优化里的“几何鞍”)
- 定义:某个临界点 x∗x^*x∗(∇f(x∗)=0\nabla f(x^*)=0∇f(x∗)=0),但它既不是局部极小也不是局部极大;沿某些方向函数值增、另一些方向减。
- 例子:f(x,y)=x2−y2f(x,y)=x^2-y^2f(x,y)=x2−y2 在 (0,0)(0,0)(0,0) 是鞍点。
2.2 极小-极大意义下的鞍点(博弈论/对偶优化里的“极小极大鞍”)
-
定义:点 (x∗,y∗)(x^*,y^*)(x∗,y∗) 满足
f(x∗,y)≤f(x∗,y∗)≤f(x,y∗)∀x,y. f(x^*,y)\le f(x^*,y^*)\le f(x,y^*)\quad \forall x,y. f(x∗,y)≤f(x∗,y∗)≤f(x,y∗)∀x,y.
它对 xxx 是“最小”,对 yyy 是“最大”。
-
意义:零和博弈的纯策略均衡、对偶优化中拉格朗日函数的原始-对偶最优刻画常用这个概念。
2.3 矩阵博弈里的“行最小列最大”(或反之)
- 定义:在支付矩阵中,若某元素是其行的最小值且又是其列的最大值(或相反),称为鞍点。
- 含义:双方都没有动机单方面偏离(一个稳定点)。
小贴士:2.2 和 2.3 是“极小极大”的思想;2.1 是“几何曲面”的思想。三个语境都叫“鞍点”,但定义不同。
3. 为什么鞍点重要?
- 优化视角:高维非凸优化(如深度学习训练)里,鞍点比严格局部极大点常见得多。在鞍点附近,梯度很小、二阶曲率正负混杂,优化算法容易“走得慢、转弯难”。
- 博弈/对偶:鞍点刻画了稳定对抗(你最小化、我最大化)的平衡点,或原始-对偶的最优一致性。
- 工程实践:识别/绕开“几何鞍”,寻找“极小极大鞍”,分别服务于数值优化和策略均衡的落地问题。
4. 如何判断“几何鞍”(微积分里的鞍点)
4.1 三步走
-
找临界点:令梯度 ∇f(x)=0\nabla f(x)=0∇f(x)=0,求解候选点 x∗x^*x∗。
-
看二阶:计算 Hessian H(x∗)=∇2f(x∗)H(x^*)=\nabla^2 f(x^*)H(x∗)=∇2f(x∗)。
-
判定类型:
- HHH 正定 ⇒ 严格局部极小;
- HHH 负定 ⇒ 严格局部极大;
- HHH 不定(既有正也有负特征值)⇒ 鞍点;
- HHH 半正定/半负定 ⇒ 二阶不够,需更高阶分析。
4.2 例子:f(x,y)=x2−y2f(x,y)=x^2-y^2f(x,y)=x2−y2
- ∇f=(2x,−2y)\nabla f=(2x,-2y)∇f=(2x,−2y),临界点只有 (0,0)(0,0)(0,0);
- Hessian H=[200−2]H=\begin{bmatrix}2&0\\0&-2\end{bmatrix}H=[200−2],特征值 222 与 −2-2−2——一正一负 ⇒ 不定 ⇒ 鞍点。
4.3 常见误区
- 一维函数没有“鞍点”(那叫拐点/变号点),鞍点是多维概念。
- Hessian 半正定不代表极小;可能需要三阶或更高阶判别(比如“猴鞍” x3−3xy2x^3-3xy^2x3−3xy2 在原点的细节更复杂)。
5. 博弈与拉格朗日意义下的鞍点
5.1 矩阵博弈的纯策略鞍点
考虑支付矩阵(行玩家最小化损失,列玩家最大化收益):
列A 列B 列C
行1 6 8 5
行2 4 7 3 ← 行最小是 3
行3 5 9 10↑列最大是 9(注意:此例没有同时“行最小 & 列最大”的元素)
若某元素同时满足“行最小 & 列最大”,它就是鞍点;双方都不愿单边改变策略。
没有这样的元素时,就要考虑混合策略均衡(概率分布上的极小极大解)。
5.2 极小-极大鞍点与拉格朗日
- 定义回顾:(x∗,y∗)(x^*,y^*)(x∗,y∗) 使 f(x∗,y)≤f(x∗,y∗)≤f(x,y∗)f(x^*,y)\le f(x^*,y^*)\le f(x,y^*)f(x∗,y)≤f(x∗,y∗)≤f(x,y∗)。
- 拉格朗日鞍点:在许多凸-凹条件和约束资格(如 Slater 条件)下,原始最优值 = 对偶最优值,且最优解对应 L(x,λ)\mathcal{L}(x,\lambda)L(x,λ) 的鞍点,配合 KKT 条件刻画最优性。
6. 优化/深度学习中的“鞍点难题”与逃逸技巧
6.1 为什么会“卡”?
- 在鞍点附近,梯度接近 0;但沿不同方向曲率一正一负,一会儿像上坡、一会儿像下坡,导致更新方向不稳定。
- 高维空间中,“严格极大点”罕见,而鞍点数量爆炸,训练过程遇到它们的概率更高。
6.2 工程上的小妙招
- 动量/Adam:累积历史梯度,减少震荡;Adam 自适应步长有助穿越平坦区域。
- 小批量噪声:SGD 的随机性像“微抖动”,有助跳出鞍点邻域。
- 学习率策略:预热 + 余弦退火、周期性重启(SGDR),避免“黏住”。
- 随机重启:从不同初始化多跑几次,减少陷入坏区域的概率。
- 正则化与归一化:如权重衰减、BatchNorm/LayerNorm 改善地形。
- 二阶/拟牛顿:在可承受的场景里用曲率信息(K-FAC、L-BFGS)更聪明地转向。
7. 实战:两种“找鞍点”的套路
7.1 几何鞍(微积分)
步骤:求 ∇f=0\nabla f=0∇f=0 → 求 Hessian → 看特征值号型。
示范:
- f(x,y)=x2−y2f(x,y)=x^2-y^2f(x,y)=x2−y2:原点是鞍点(见 §4.2)。
- “猴鞍” f(x,y)=x3−3xy2f(x,y)=x^3-3xy^2f(x,y)=x3−3xy2:原点是临界点,但 Hessian 为零矩阵(不够判别);需看更高阶项,分析得出原点呈“多向下坡/上坡”的鞍状结构。
7.2 极小极大鞍(博弈/对偶)
步骤:检查 xxx 方向的最小值与 yyy 方向的最大值是否在同一点结合;
凸-凹结构下常可用极小极大定理保证等式与鞍点存在性。
在矩阵博弈里,若纯策略鞍点不存在,就求混合策略均衡(线性规划或对偶形式)。
8. 口袋速查表(Cheat Sheet)
- 几何鞍:∇f=0\nabla f=0∇f=0 且 Hessian 不定。
- 极小极大鞍:f(x∗,y)≤f(x∗,y∗)≤f(x,y∗)f(x^*,y)\le f(x^*,y^*)\le f(x,y^*)f(x∗,y)≤f(x∗,y∗)≤f(x,y∗)。
- 矩阵鞍:元素是“行最小 & 列最大”(或行最大 & 列最小)。
- 深度学习:动量/Adam + 噪声 + 学习率策略 + 正则/归一化 +(可选)二阶近似。
