1.数值分析——概述、误差
考核方式 办公室B306
讨论
随堂测验
章节测验
计算题PPT展示(学习通资料有电子版):理论、计算过程、程序
实验报告(20分):计算实习题
数值分析解决什么问题?
用计算机解决计算问题
问题转换——模型设计——算法设计——程序设计——计算求解
数值分析的结果是一组离散的数值解
数值分析基本方法
采取的方法有:
数值逼近、数值微分与数值积分、非线性方程组数值解、数值线性代数、常微与偏微数值解
常用程序软件:Matlab 、MWORKS
误差来源
-
模型误差
对次要因素的忽略,对环境的理想化 -
测量误差
测量过程中产生的观测误差 -
截断误差
对难以求解的数学模型进行近似产生的误差,如:泰勒公式,此时截断误差为泰勒余项。 -
舍入误差
计算机只能进行的有限的数位运算,进行舍入产生的误差。
误差
为直观理解,假设一条河宽100m(实际上由于难以测量,未知),估计值是101m。
绝对误差、绝对误差限(误差限)
绝对误差
若准确值为x,其近似值为x*,则其绝对误差e* = x* - x,具体的数。
此处真实值x = 100,近似值 x* = 101,绝对误差e* = 1
由于真实值很难获取,故绝对误差很难获得。
绝对误差限
由于绝对误差很难获得,那么我们允许一定范围内的误差认定是合理的。这个认定的误差上界,称为近似值x*的 绝对误差限,记为ε*,这是上界,或者说是浮动范围。
则精确值x可表示为:
x = x* ± ε*
此处,假设2m内的误差都可以接受,即ε* = 2,此时x = [99,103]
相对误差、相对误差限
相对误差
绝对误差e*与准确值x的比值,有
e∗x=x∗−xx\frac{e*}{x} = \frac{x*-x}{x}xe∗=xx∗−x
由于真值x总是未知的,所以这里通常取x*替代,称为近似值x*的相对误差 er*,这是具体误差值与近似值的比值。
er∗=e∗x∗=x∗−xxer* = \frac{e*}{x*} = \frac{x*-x}{x}er∗=x∗e∗=xx∗−x
此处,相对误差er* = 1/101 = 0.0099…
但是还有一个问题,就是e*事实上也是不知道的
相对误差限
所以引入了相对误差限,我们允许相对误差在一定范围合理,为相对误差设置绝对值的上界,称为相对误差限εr*
εr∗=ε∗∣x∗∣εr* = \frac{ε*}{|x*|}εr∗=∣x∗∣ε∗
此时,εr* = 2/101 = 0.0198…
在实际计算中,相对误差限可以进一步表示如下:
εr∗=ε∗∣x∗∣=∣x∗−x∣∣x∗∣=∣er∗∣εr* = \frac{ε*}{|x*|} = \frac{|x*-x|}{|x*|}=|er*|εr∗=∣x∗∣ε∗=∣x∗∣∣x∗−x∣=∣er∗∣
绝对误差不超过末尾有效数字的半个单位
x∗=±10m(a1+a2⋅10−1+...+an⋅10−(n−1))x* = ±10^m(a_1 + a_2 · 10^{-1}+ ... +a_n · 10^{-(n-1)})x∗=±10m(a1+a2⋅10−1+...+an⋅10−(n−1))
εr∗=∣x−x∗∣≤12⋅10(m−n+1)εr* = |x - x^*| \leq\frac{1}{2}· 10^{(m-n+1)}εr∗=∣x−x∗∣≤21⋅10(m−n+1)
要求掌握:
由近似值找相对误差限,由相对误差限得有几位有效数字
例题1

误差运算法则
设两个近似数x1*,x2*,其相对误差分别为ε*(x1*)和ε*(x2*),有如下运算法则。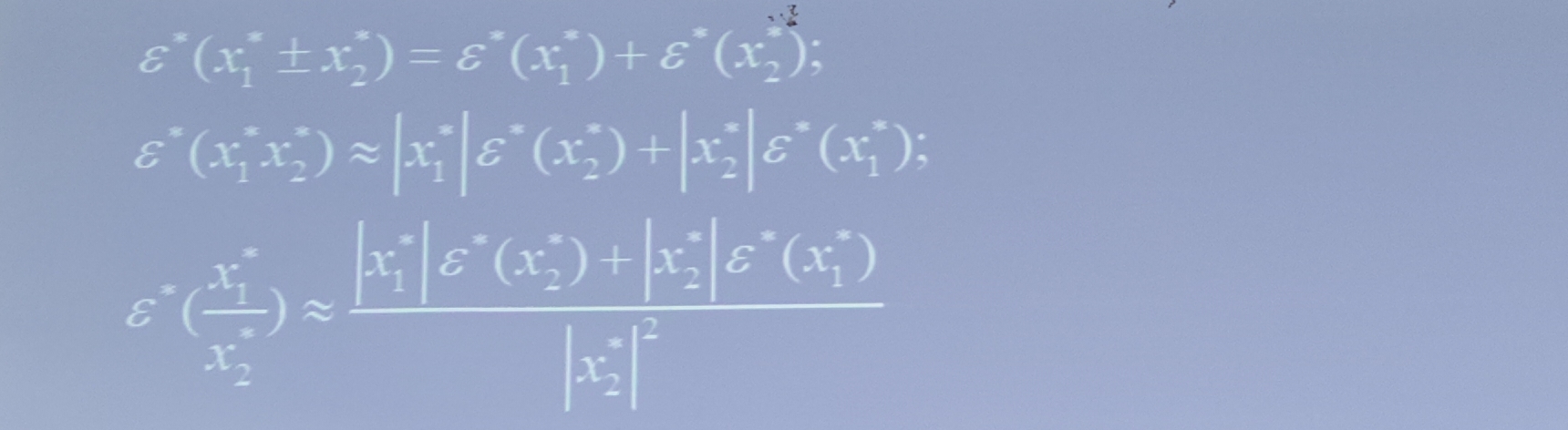


200是近似值,5是绝对误差限
避免误差原则
避免大数除小数
浮点数对阶截断
避免相近数相减
两个非常接近的数相减时,它们的高位有效数字会相互抵消,导致结果中只剩下低位的不太可靠的数字。


大数吃小数
归一化,小数合到一起算
简化步骤,减少运算次数
数学方法降维,简化计算,少用递归,多用加减少用乘除

