当前位置：首页 > news >正文

液态神经网络（LNN）2：LTC改进成CFC详细推导过程

news 2025/9/2 6:39:48

第一步：LTC 的微分方程 (原始形式)

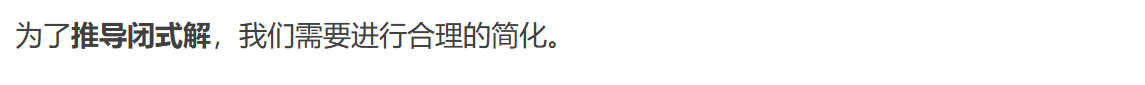
第二步：简化假设 (为推导做准备)

第三步：求解线性非齐次ODE

首先，处理（4）式最外层的前缀项 $e^{-\int_0^t f(I(s)) ds}$ 。这里应用了第一个关键近似：

理由：如果输入 $I(t)$ 变化足够缓慢，或者时间区间 [0, t]$足够小，那么 $f(I(s))$ 在这个区间内可以近似看作一个常数 $f(I(t))$ 。对这个常数进行积分，自然就得到了 $f(I(t)) \cdot t$ 。

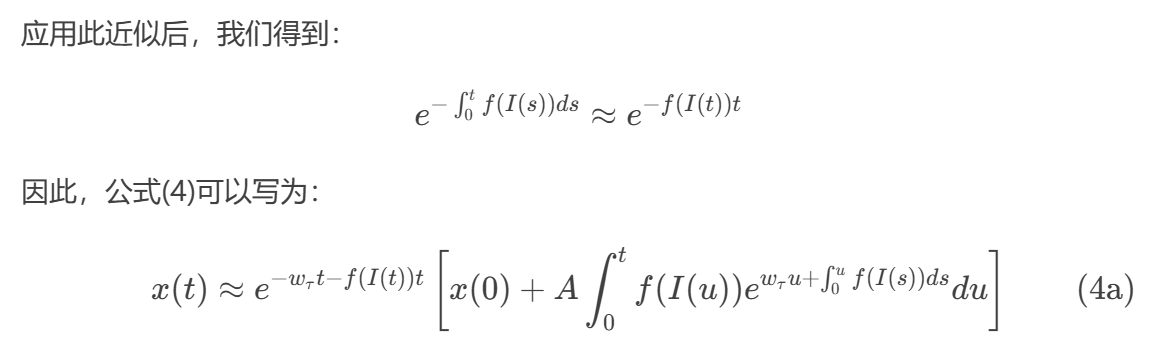
第四步：处理内部的复杂积分项

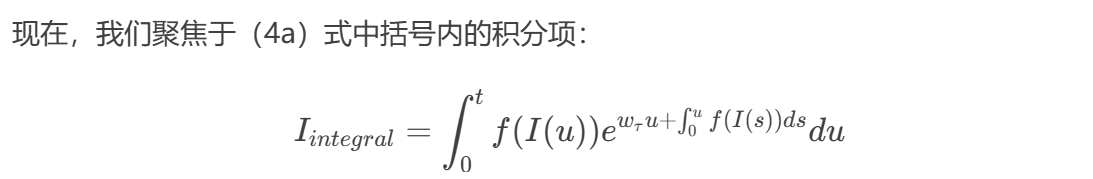
那么，其对 $u$ 的导数为：

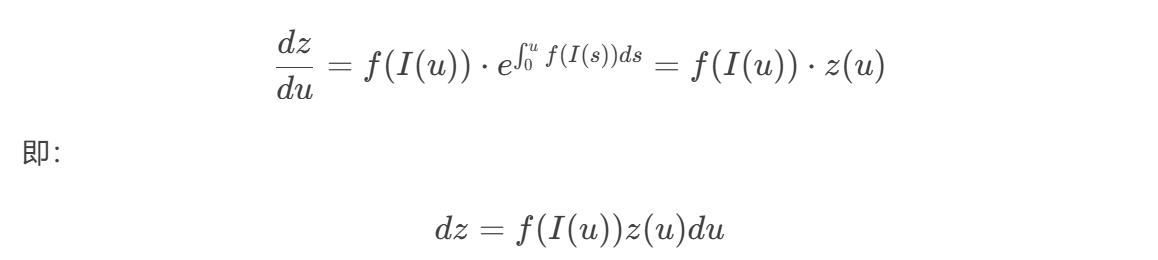
现在，我们仔细观察 $I_{integral}$ ：

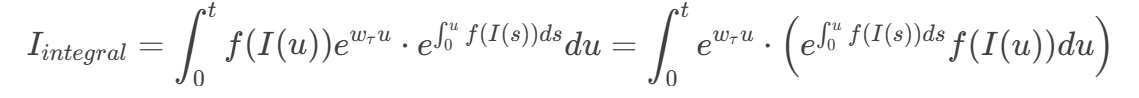
注意到括号内的项正好是我们的 $dz$ 所以，积分可以转化为：

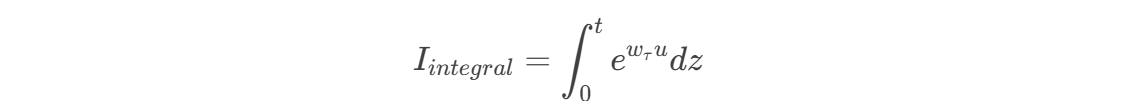
这是一个关于变量 $z$ 的积分。为了计算它，我们使用分部积分法。

分部积分法： $\int u dv = uv - \int v du$
令：
$v = z \quad \Rightarrow \quad dv = dz$
$u = e^{w_\tau u} \quad \Rightarrow \quad du = w_\tau e^{w_\tau u} du$ (注意这里 $u$ 既是函数又是积分变量，稍需注意区分)

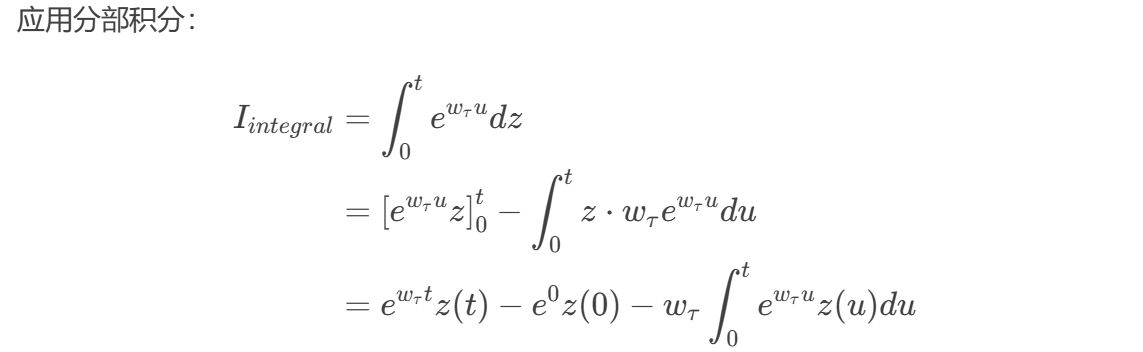
我们知道 $z(0) = e^{\int_0^0 f(I(s)) ds} = e^0 = 1$ ，且 $z(t) = e^{\int_0^t f(I(s)) ds}$ 。代入上式：

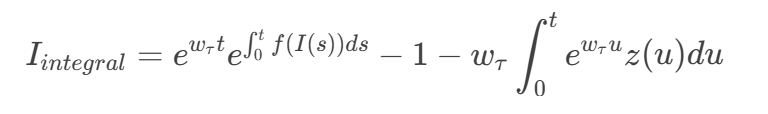（5）

公式(5)看起来更复杂了，但它引入了一项 $e^{w_\tau t} e^{\int_0^t f(I(s)) ds}$ ，这是我们想要的。

第五步：关键的“灵感飞跃”式近似

观察公式(5)，它仍然包含一个积分项 $\int_0^t e^{w_\tau u} z(u) du$ 。为了闭合（得到一个封闭形式的解），作者进行了最大胆的近似。

近似2：假设积分项的主要贡献来自其自身的某种形式
观察整个表达式，作者注意到 $I_{integral}$ 应该与一个形如 $ $e^{w_\tau t} e^{\int_0^t f(I(s)) ds} f(-I(t))$ 的项有关。 $f(-I(t))$ 的引入是为了保持数学上的对称性，并使得最终解在 $f(\cdot)$ 是Sigmoid函数时， $f(-I(t))$ 可以看作 $(1 - f(I(t)))$ ，形成一个类似门控的结构。

因此，他们直接假设通过这种近似，积分项 $I_{integral}$ 可以被表示为：

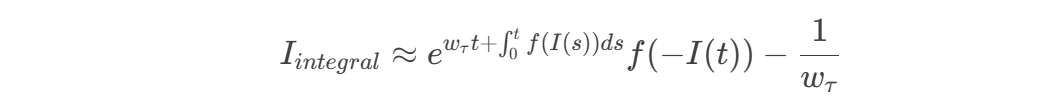（7）

(注意：这里 $- \frac{1}{w_\tau}$ 项是为了在后续步骤中消去常数项而设定的)

更常用且更简洁的写法是，利用之前的近似1，将 $\int_0^t f(I(s)) ds$ 替换为 $f(I(t)) t$ ：

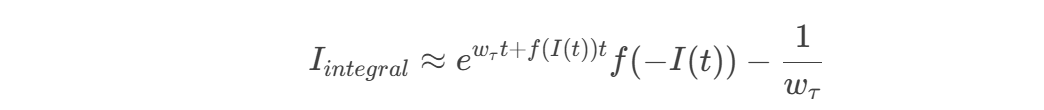（7a）

第六步：将近似积分代回原式

现在我们将近似后的积分结果（7a）代回到原始表达式（4a）中：

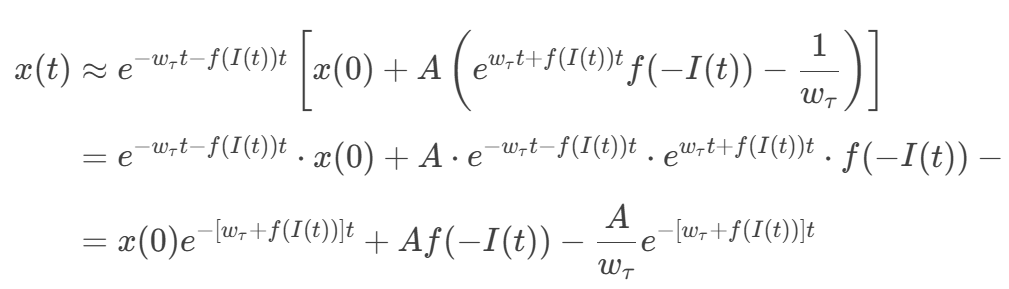
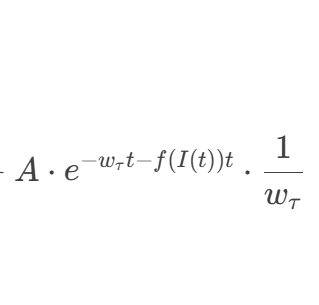
第七步：最终简化与常数吸收

上式最后一项 $-\frac{A}{w_\tau} e^{-[w_\tau + f(I(t))] t}$ 在 $t$ 较大时会衰减到0。为了得到更简洁、更稳定的形式，作者忽略了这一项，并将剩余的常数项合并。

将 $A f(-I(t))$ 拆解和重组：

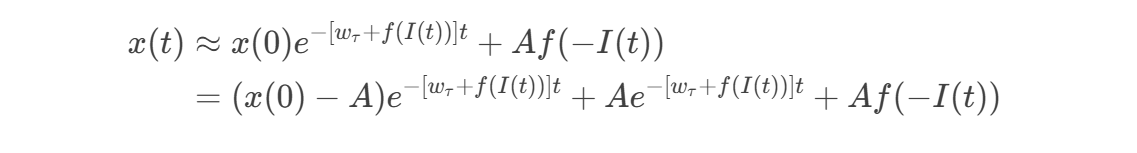
注意到 $A e^{-[\ldots] t} + A f(-I(t))$ 仍然不完美。最终的“神来之笔”是将 $A$ 提取出来，并假设 $e^{-[\ldots] t} + f(-I(t)) \approx 1$ 。这个假设在 $f$ 是Sigmoid函数且 $f(-I(t)) \approx 1 - f(I(t))$ 时尤其合理，因为 $e^{-f(I(t))t}$ 和 $1 - f(I(t))$ 在数值行为上有相似之处。

通过这种直觉性的简化，我们得到了最终的目标公式：

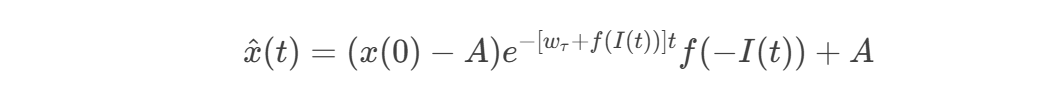
总结与评论

从 (4) 到 (5) 的推导并非传统的严格数学推导，而是一个构造性的近似过程：

近似1： $\int_0^t f(I(s)) ds \approx f(I(t)) \cdot t$ （用终点值代表积分）
技巧：变量代换和分部积分，将问题重新表述。
近似2：直接假设积分项 $I_{integral}$ 的解的形式，引入 $f(-I(t))$ 以构造门控机制。
简化：忽略高阶衰减项，基于对函数行为的直觉进行重组和简化。

这个过程的正确性并非由推导的严格性保证，而是由后续的Lemma 1证明的误差界 $|x(t) - \hat{x}(t)| \leq |x(0)-A|e^{-w_\tau t}$ 来保证的。只要误差足够小且可控，这个近似就是有效且有用的。它用数学上的一点“不严谨”换来了计算效率上几个数量级的提升，这就是CfC工作的核心贡献。