Day19_【机器学习—线性回归 (3)—回归模型评估方法】

六、回归模型评估方法（MAE、MSE、RMSE）

        线性回归模型评估中，MAE、MSE和RMSE是三种常用的指标，它们各自从不同的角度衡量预测值与真实值之间的差距。

1. 平均绝对误差（Mean Absolute Error, MAE）

• 定义：MAE计算的是预测值与真实值之间绝对差值的平均值。
• 公式：

                        ​​​​​​​        ​​​​​​​        

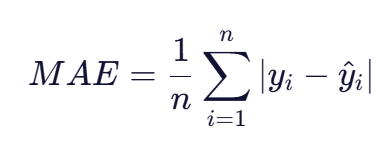
其中，nn为样本数量，yiyi​为第 ii个样本的真实值，y^iy^​i​为对应的预测值。

• 特点：MAE对异常值相对不敏感，因为它使用绝对值来计算误差，不会因为少数大误差而过分影响整体结果。
• Python实现：

from sklearn.metrics import mean_absolute_error
print(mean_absolute_error(y_test, y_predict))

2. 均方误差（Mean Squared Error, MSE）

• 定义：MSE计算的是预测值与真实值之间差值平方的平均值。
• 公式：

                                      

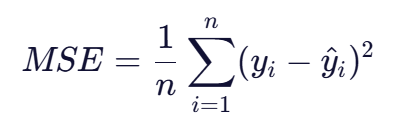
特点：MSE对异常值非常敏感，因为误差被平方了，所以较大的误差会被放大，这使得MSE在数据集中有异常值时可能不是最佳选择。

• Python实现：

from sklearn.metrics import mean_squared_error
print(mean_squared_error(y_test, y_predict))

3. 均方根误差（Root Mean Squared Error, RMSE）

• 定义：RMSE是MSE的平方根，它将MSE转换回与原始数据相同的单位，从而更直观地理解误差大小。
• 公式：

                                        

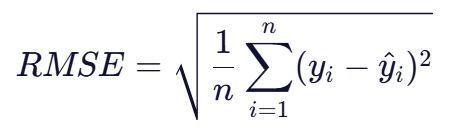
• 特点：RMSE同样对异常值敏感，但相比于MSE，它提供了更易于解释的误差度量，因为它的单位与原始数据相同。在某些情况下，RMSE比MSE更有用，尤其是在需要直接比较预测值与真实值差异的场景中。
• Python实现：

from sklearn.metrics import root_mean_squared_error
print(root_mean_squared_error(y_test, y_predict))