leetcode_48 旋转图像
1. 题意
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
2. 题解
2.1 暴力
我们先通过暴力弄明白是怎么转的,顺时针旋转90度;
实际上就是把第一行变成了倒数第一列,第二行变成了倒数第二列。
因此我们可以写出旋转前后的对应关系
matrix[i][j]=new_matrix[j][n−1−i]matrix[i][j] = new\_matrix[j][n-1-i] matrix[i][j]=new_matrix[j][n−1−i]
用一个新的数组来记录这个新数组,最后再把新数组的值给赋值回来
不就好了吗?
当然这是不符合原地的空间复杂度要求的。
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();vector<vector<int>> sup(n, vector<int>(n));for (int r = 0;r < n; ++r ) {for (int c = 0; c < n; ++c) {sup[c][n - r - 1] = matrix[r][c];}}matrix = sup;}
};
2.2 转置+反转
如果学过矩阵的话,会知道有一种操作叫转置,也就是行列之间互换。
第一行变成了第一列,第二行变成了第二列。
但是这跟我们上面的要求还不符?怎么办呢?
我们反转一下不就好了吗?
反转列是典型的相向双指针不用多说。
而对于转置操作,就是行列互换。
at[i][j]=a[j][i]at[i][j] = a[j][i] at[i][j]=a[j][i]
(i,j),(j,i)(i,j),(j,i)(i,j),(j,i)关于r=cr=cr=c对称,
我们只需要枚举所有的i>ji>ji>j或者i<ji<ji<j的点进行交换就可以了。
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();for (int i = 0; i < n; ++i) {for (int j = 0; j < i; ++j) {if (i != j) {std::swap(matrix[i][j], matrix[j][i]);}}}for ( int i = 0; i < n; ++i) {int l = 0,r = n - 1;while (l < r) {std::swap(matrix[i][l], matrix[i][r]);l++;r--;}}}
};
2.3 原地旋转
由于有四个方向,每次旋转完后的位置有新的数了。
因此我们需要对于一个位置一直旋转到结束循环为止。
我们假设起始的位置在(i,j)(i,j)(i,j)
上面我们已经知道了它顺时针旋转90度后的位置在(j,n−1−i)(j,n-1-i)(j,n−1−i)
那这个新位置旋转后在哪里呢?
直接代入上面的情况就行了,新的位置在(n−1−i,n−1−j)(n - 1 -i, n- 1 - j)(n−1−i,n−1−j)
继续寻找下一个新位置,下一个新位置在(n−1−j,i)(n - 1 - j, i)(n−1−j,i)
继续寻找下一个新位置,下一个新位置在(i,j)(i , j)(i,j)
这样就构成了一个loop:
(i,j)→(j,n−1−i)→(n−1−i,n−1−j)→(n−1−j,i)→(i,j)(i,j) \to(j,n-1-i) \to (n-1-i, n-1-j) \\ \to(n-1-j,i) \to (i, j) (i,j)→(j,n−1−i)→(n−1−i,n−1−j)→(n−1−j,i)→(i,j)
对于每个变换的位置,我们只需要按上面的顺序处理就可以了。
接下来要做的是找到所有的需要处理的位置,要不重不漏。
首先是偶数的情况,
很显然只需要处理0≤i<n/2,0≤j<n/20\le i < n/2,\ 0 \le j < n/20≤i<n/2, 0≤j<n/2的情况就可以了。
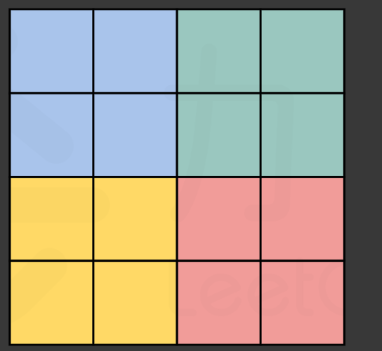
其次是奇数的情况,看下面的图吧。
中间的点我们不需要处理。
对于行来说,0≤i<⌊n/2⌋0 \le i < \lfloor n/2 \rfloor0≤i<⌊n/2⌋
对于列来说,0≤j≤⌈n/2⌉0 \le j \le \lceil n/2 \rceil0≤j≤⌈n/2⌉

综合两种情况看
0≤i<⌊n/2⌋0≤j<⌊(n+1)/2⌋0 \le i < \lfloor n/2\rfloor\\ 0 \le j < \lfloor (n+1)/2 \rfloor 0≤i<⌊n/2⌋0≤j<⌊(n+1)/2⌋
这种方法也就是官方的做法了
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();for (int i = 0; i < n / 2; ++i) {for (int j = 0; j < (n + 1) / 2; ++j) {int tmp = matrix[i][j];matrix[ i ][ j ] = matrix[ n - 1 - j ][ i ];matrix[ n - 1 - j ][ i ] = matrix[ n - 1 - i ][ n - 1 - j ];matrix[ n - 1 - i ][ n - 1 - j ] = matrix[ j ][ n - 1 - i ];matrix[ j ][ n - 1 - i ] = tmp;}}}
};
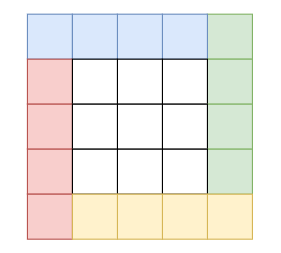
另外一种做法是基于层来做旋转,如下图所示.
假设当前层的左端和上端的值为mn,
下端和右端的值为mx。
对于上端的点(mn,i)(mn, i)(mn,i),它所在的圈层容易求出为
(mn,i)→(i,mx)→(mx,mx−(i−mn))→(mx−(i−mn),mn)→(mn,i)(mn,i) \to(i, mx) \to(mx, mx-(i-mn))\\ \to(mx-(i-mn), mn) \to(mn,i) (mn,i)→(i,mx)→(mx,mx−(i−mn))→(mx−(i−mn),mn)→(mn,i)
对于每一层来说, 我们只需要遍历(mn,i),mn≤i<mx(mn,i), mn \le i < mx(mn,i),mn≤i<mx。
在一层处理完成后,左右边界往中间收缩,一直处理到mn≥mxmn \ge mxmn≥mx。
代码
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n = matrix.size();int mx = n - 1;int mn = 0;while ( mn < mx) {for (int i = mn; i < mx; ++i) {swap(matrix[mn][i], matrix[i][mx]);swap(matrix[mn][i], matrix[mx][mx - (i - mn)]);swap(matrix[mn][i], matrix[mx - (i - mn)][mn]);}++mn;--mx;}}
};
参考
leetcode
