C/C++ 高阶数据结构 —— 二叉搜索树(二叉排序树)


🎁个人主页:工藤新一¹
🔍系列专栏:C++面向对象(类和对象篇)
🌟心中的天空之城,终会照亮我前方的路
🎉欢迎大家点赞👍评论📝收藏⭐文章
文章目录
- 二叉查找树 OR 二叉排序树(BST)
- 一、核心概念:一句话定义
- 二、二叉查找树的删除
- 2.1删除叶子节点
- 2.2删除度为1的节点
- 2.3删除分支节点
- 2.3.1普通分支节点
- 2.3.2根节点
- 三、核心逻辑实现
- 3.1二叉搜索树查找逻辑
- 3.2二叉搜索树插入逻辑
- 3.3二叉搜索树删除逻辑
- 3.4丢弃递归返回值问题
二叉查找树 OR 二叉排序树(BST)
二叉查找树和二叉排序树是完全同一个概念,指的是同一种数据结构,其也是面试常客
二叉树具体的呈现:

删除与插入的处理方式都需以查找为基础
在标准的二叉搜索树(BST)定义中:
- ✅ 通常不允许重复元素
- ✅ 每个节点的键值(key)都是唯一的
- ✅ 遵循严格的大小关系:左子树 < 根节点 < 右子树
一、核心概念:一句话定义
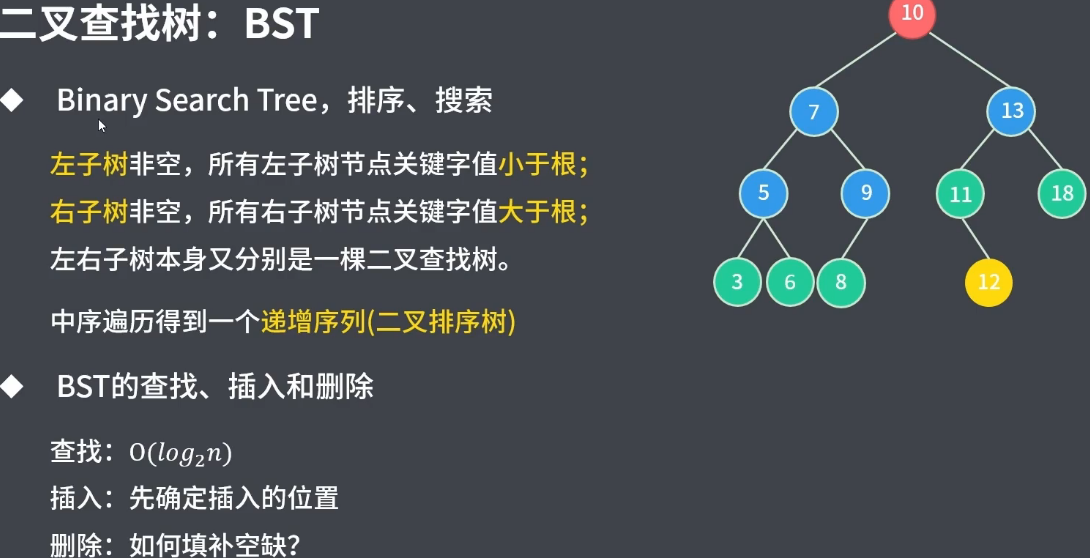
二叉查找树是一种特殊的二叉树,他给它的节点立下了严格的“规矩”:对于树中的任意一节点,其左子树中所有 节点值都必须小于根节点,其右子树中所有 节点值都必须大于其根节点
这个“规矩”就是二叉查找树的灵魂,它的一切神奇特性都源于此
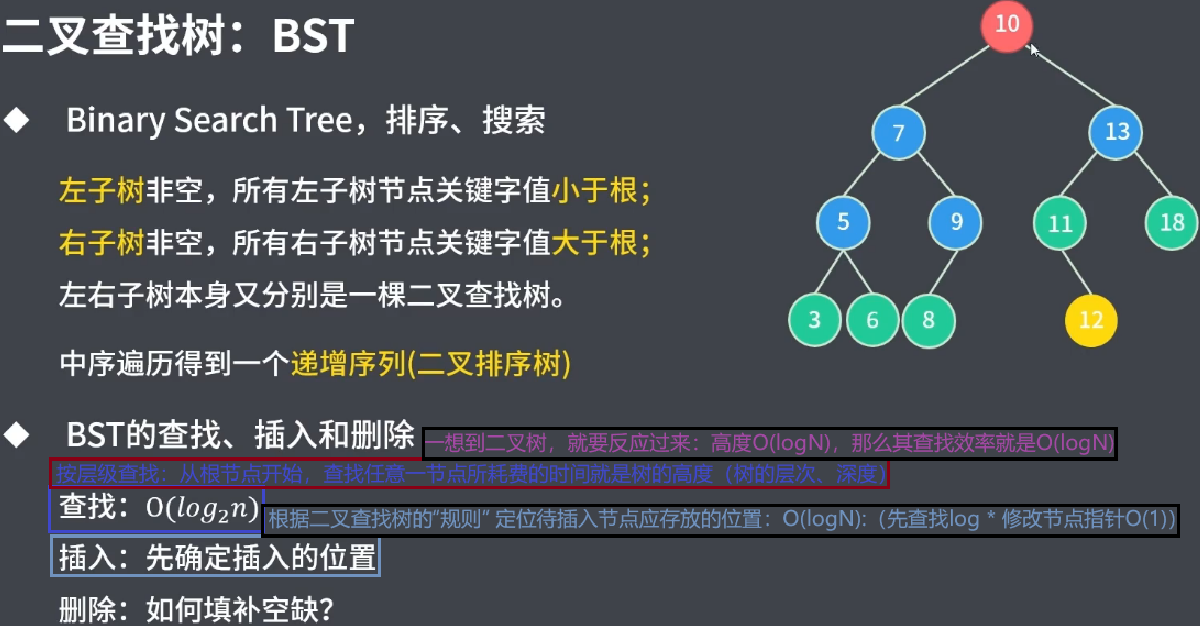
二、二叉查找树的删除
重点问题:如何填补空缺(节点),才能保持整个二叉树的结构不发生变化,且不违反其定义?
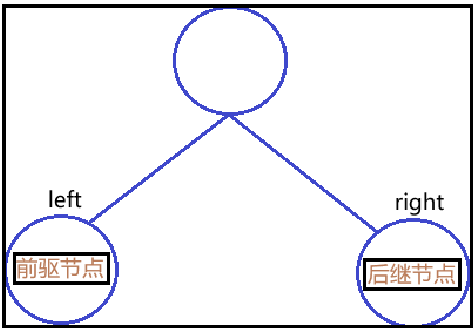
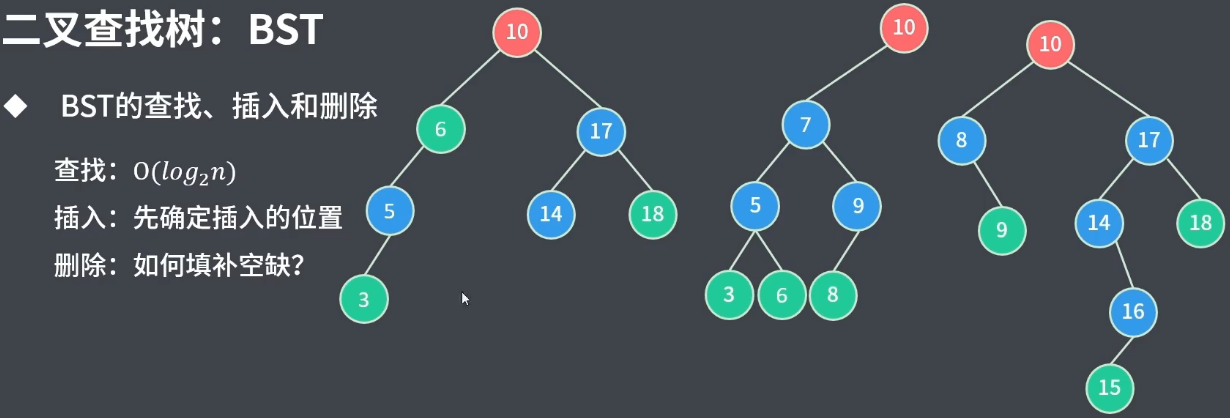
2.1删除叶子节点
删除node3:
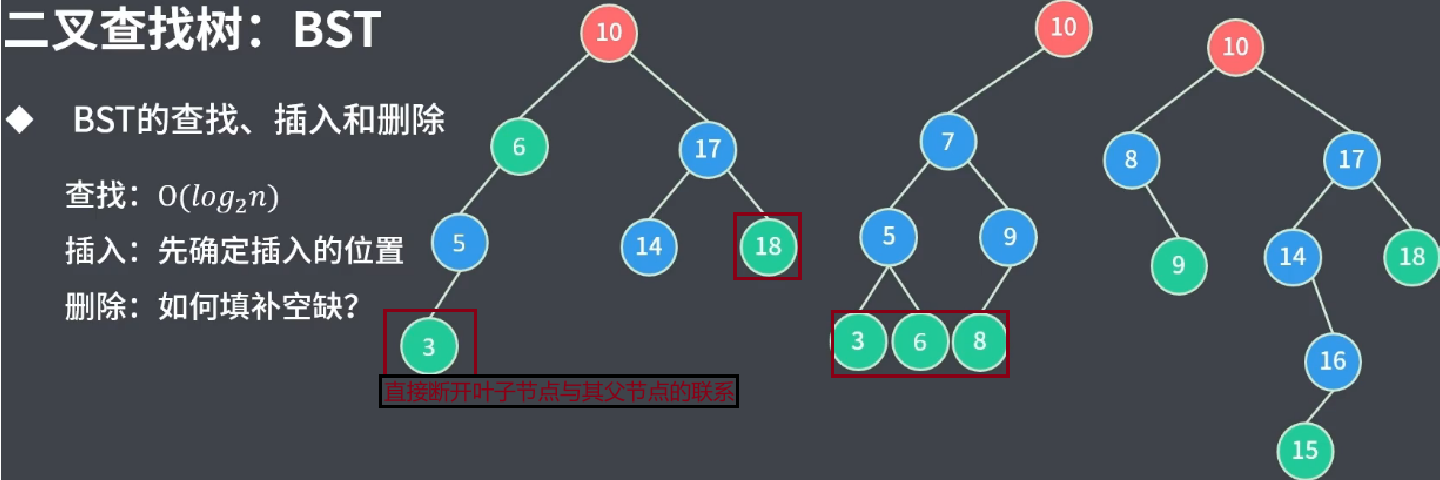
2.2删除度为1的节点
删除node6:
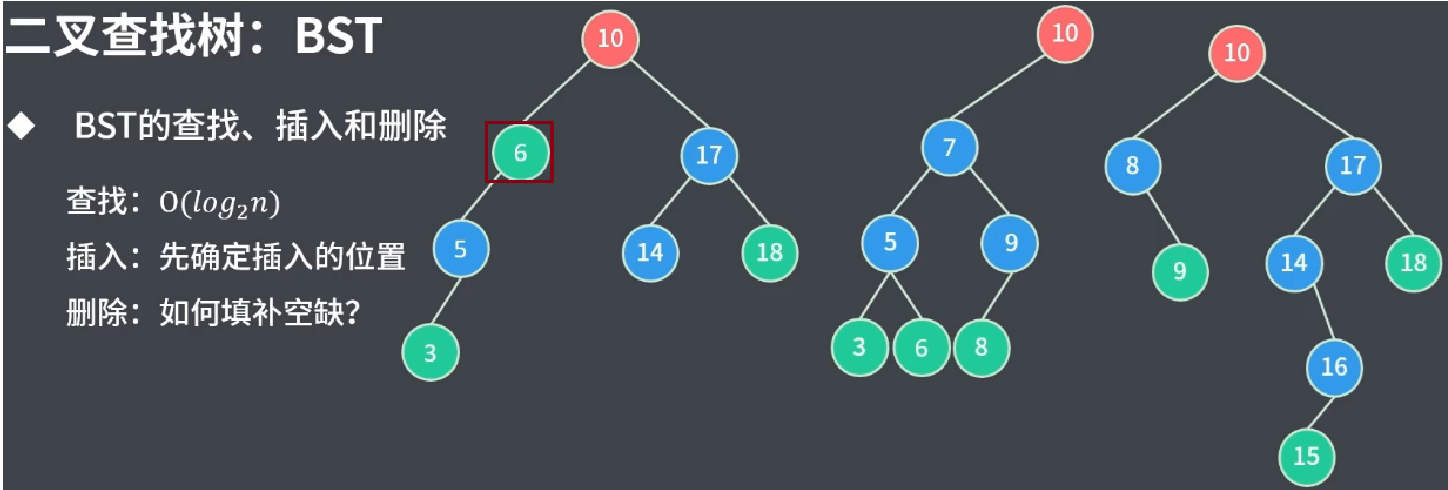
我们观察node6只有左子树,那么可以直接将 node6->left(node6的前驱节点:node5)放入node6所在的位置
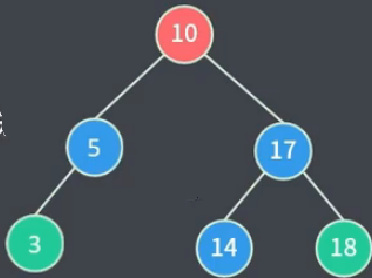
因此,删除度为1的节点,我们可以直接将其 左 or 右子树,放在(占用)当前节点所处的位置上即可(其余节点不需调整)
2.3删除分支节点
2.3.1普通分支节点
删除node7:
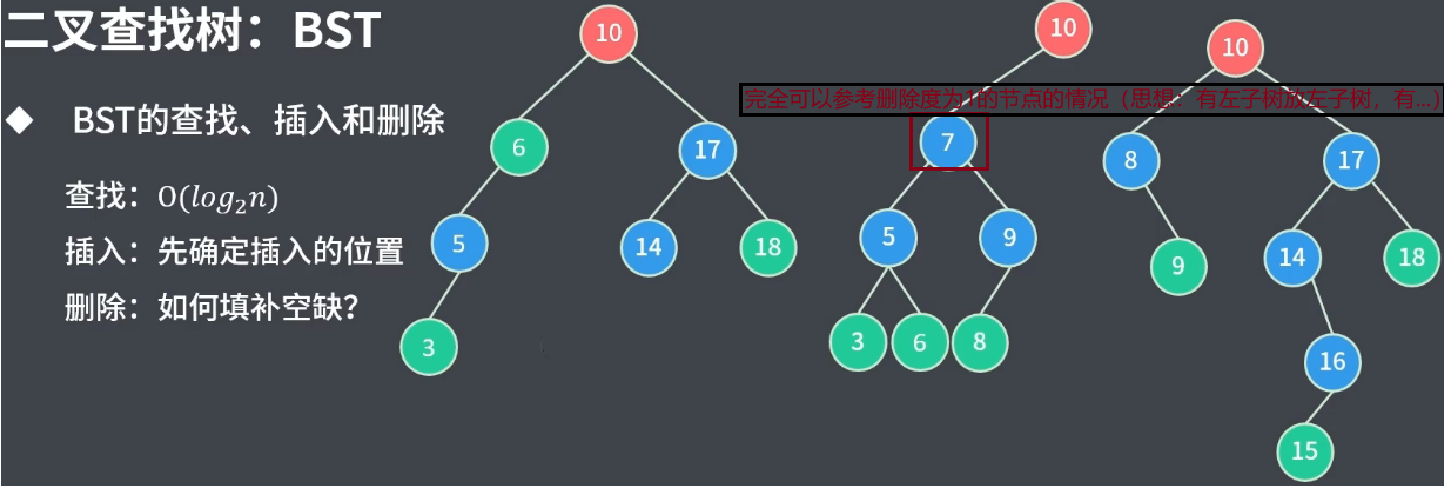
我们可以参考删除度为1节点的逻辑:将 node7的 前驱/后继节点 占用到node7的位置上
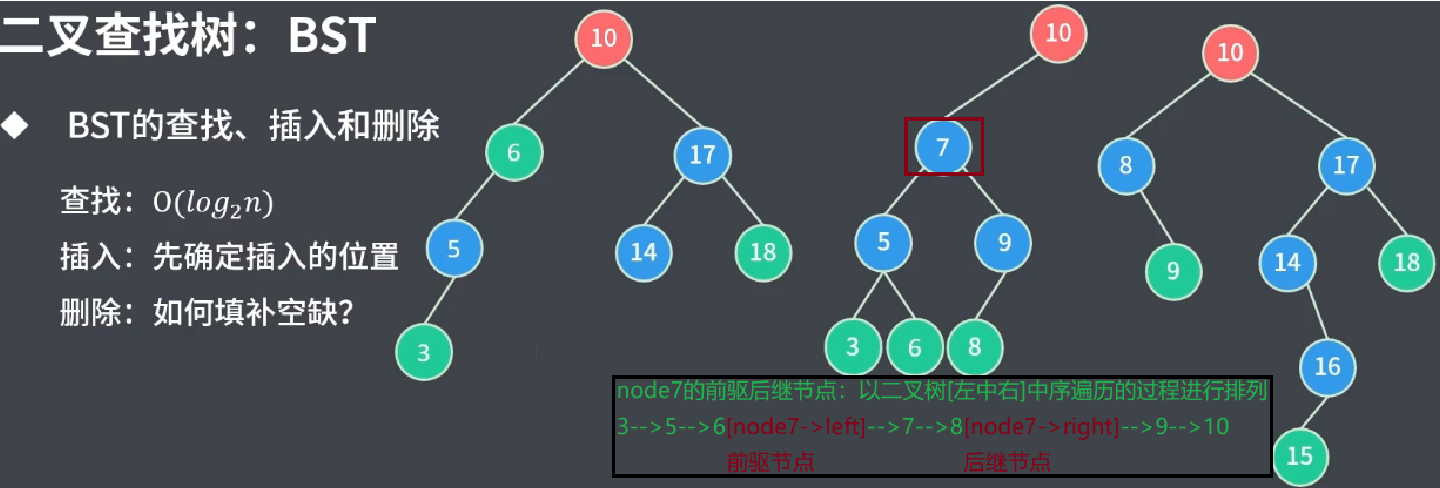
将 node7的前驱节点(node->left)node6放置node7 所处位置上
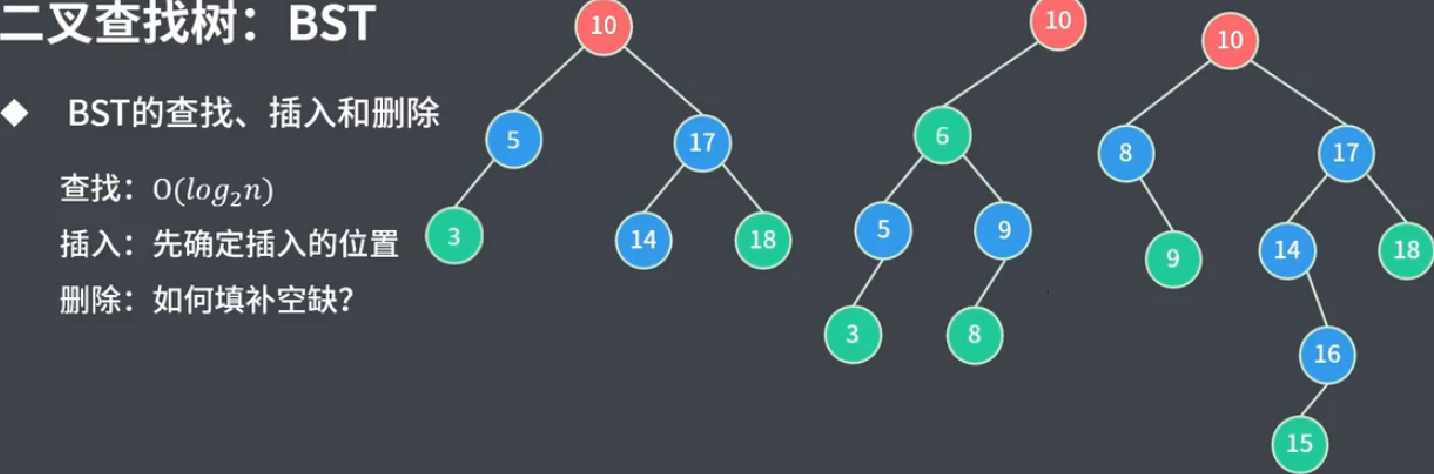
2.3.2根节点
O(logN)[查找删除根节点] * O(1)[删除] * O(logN)[查找替换根节点的根节点的后继/前驱节点] * O(1)[删除]
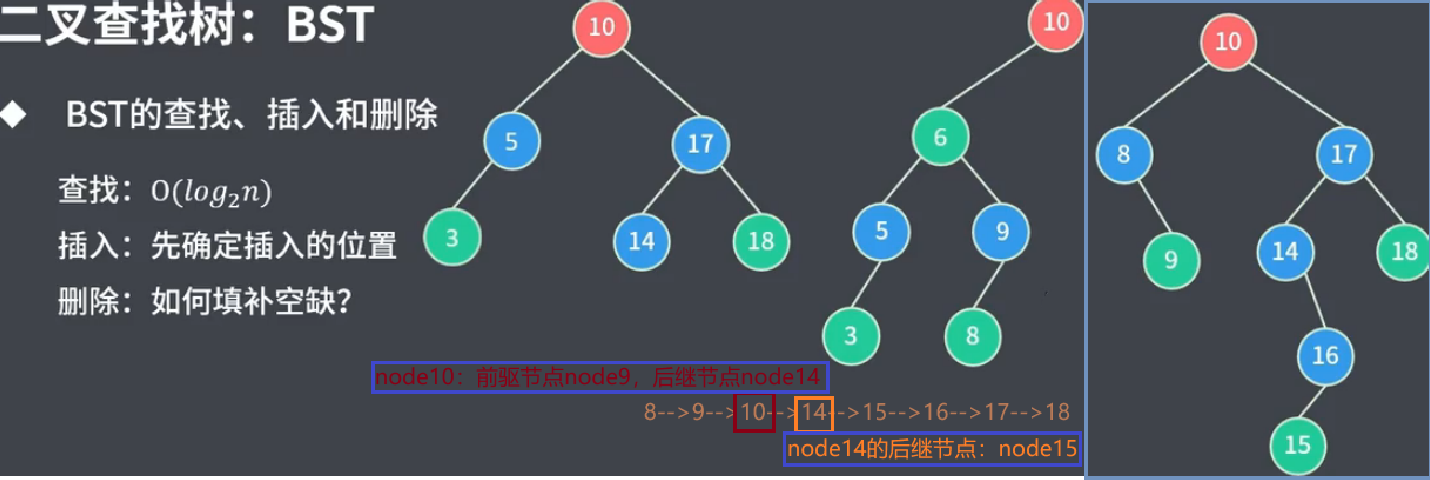
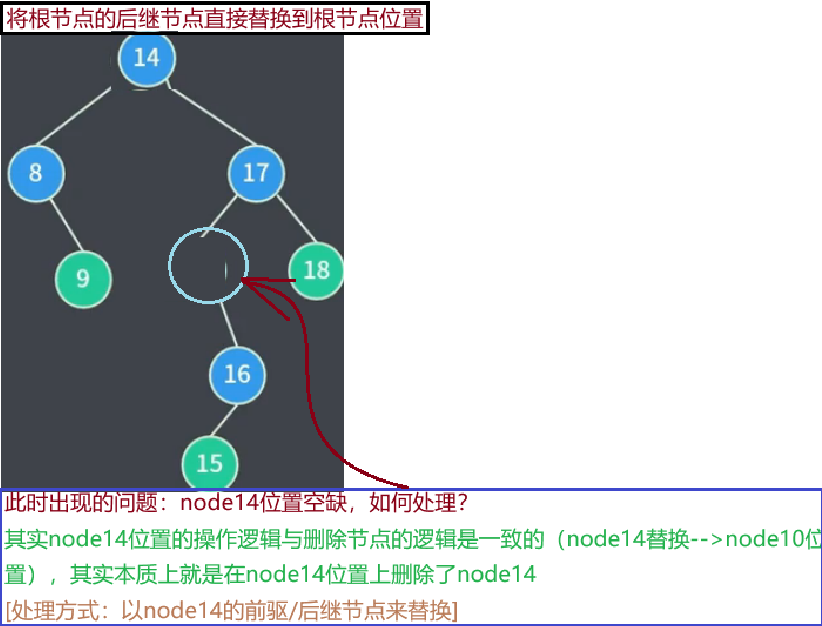
最终形成的逻辑结果:
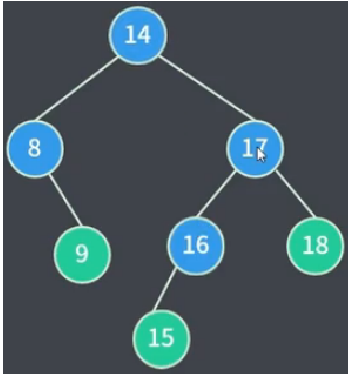
问题:既然 node14 的后继节点是 node15,那么为什么不是:
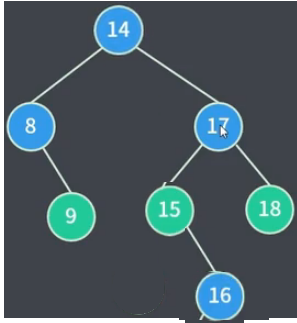
这是因为,我们已知 node14 只有右子树(即node14度为1),那么我们就可以直接利用 “节点度为1” 的情况的处理方式来进行节点的替换。正常对于二叉树的树形结构不清楚时,一定是要判断对应删除的节点的前驱后继节点(处理方式:递归查找),进行对应删除替换逻辑
删除度为2的节点,其实是对整个树的递归式的删除(将对应节点的前驱/后继指针删除后再替换至当前删除位置,并且可能会产生二次替换:将当前节点的前驱/后继节点的前驱/后继替换到当前前驱/后继节点的位置上;第三次替换:…)
但实际上,搜索时间复杂度最差的情况为:O(N)
从根节点–>最终的叶子节点 == 树的高度
树形结构中树的高度:logN
线性树形结构中树的高度:N(即整个树的节点个数)
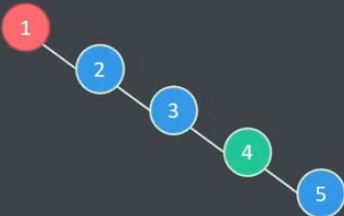
二叉树
- 逻辑结构上:树形结构
- 存储结构上:线性的单链表结构,因此就有了O(N)的时间复杂度
三、核心逻辑实现
二叉搜索树(或:二叉排序树),其最主要的特点:中序遍历会得到一个递增序列,无论是 查找/排序 都可以非常高效的实现。在实际生产过程中 二叉排序树 是所运用到的最主要的树形结构
创建搜索二叉树:
// 定义树节点存储的数据类型
typedef int ElemType;// 定义树的节点类型
typedef struct BinarySearchTree
{ElemType data;struct BinarySearchTree* left, * right;// 构造函数 - 初始化字段BinarySearchTree(int val) :data(val), left(nullptr), right(nullptr) { }
} TreeNode;
3.1二叉搜索树查找逻辑
-
1.对比待查找关键字值与当前节点的数据域
-
2.关键字值 < 数据域:向左子树递归查找
-
3.关键字值 > 数据域:向右子树递归查找
-
复杂度分析:
空间复杂度:O(1) - 无需额外定义其他空间 时间复杂度(树的所有动作都是基于查找来执行):查找次数与树的高度(层次)等价 - O(logN)
二叉树中序遍历(递归)– 算法分离:
时间复杂度:O(N)
- 遍历函数:
void InOrderByRec(TreeNode* node)
{if (!node) return;InOrderByRec(node->left);cout << node->data << "->";InOrderByRec(node->right);
}
- 查找函数:
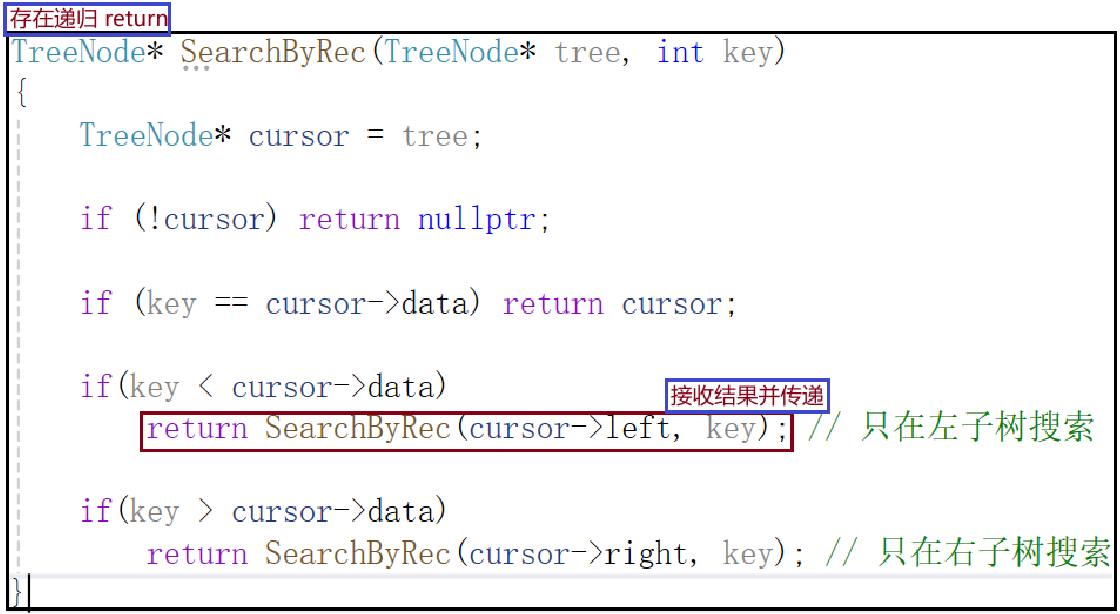
TreeNode* SearchByRec(TreeNode* tree, int key)
{TreeNode* cursor = tree;if (!cursor) return nullptr;if (key == cursor->data) return cursor;if(key < cursor->data)return SearchByRec(cursor->left, key); // 只在左子树搜索if(key > cursor->data)return SearchByRec(cursor->right, key); // 只在右子树搜索
}
简洁代码(三目表达式):
C++return (key < cursor->data) ? SearchByRec(cursor->left, key) : SearchByRec(cursor->right, key);
二叉树中序遍历(循环):
时间复杂度:O(logN)
TreeNode* SearchByFor(TreeNode* tree, int key)
{TreeNode* cursor = tree;while (cursor){if (key == cursor->data) return cursor;if (key < cursor->data) cursor = cursor->left;if (key > cursor->data) cursor = cursor->right;}return nullptr;
}
3.2二叉搜索树插入逻辑
- 1.查找插入位置
- 2.新建节点,执行插入动作
- 3.返回操作标志
迭代逻辑:
bool Insert(TreeNode* tree, int key)
{if (!tree){tree = new TreeNode(key);return true;}// 1.查找插入的位置TreeNode* pos = tree, * parent = nullptr;// while循环结束意味着整个树的高度查找结束while (pos){// 迭代更新 parent 成为 pos 父节点parent = pos;if (key == pos->data) return false;if (key < pos->data) pos = pos->left;if (key > pos->data) pos = pos->right;}// 2.新建节点,执行插入动作if (key < parent->data) parent->left = new TreeNode(key);if (key > parent->data) parent->right = new TreeNode(key);return true;
}
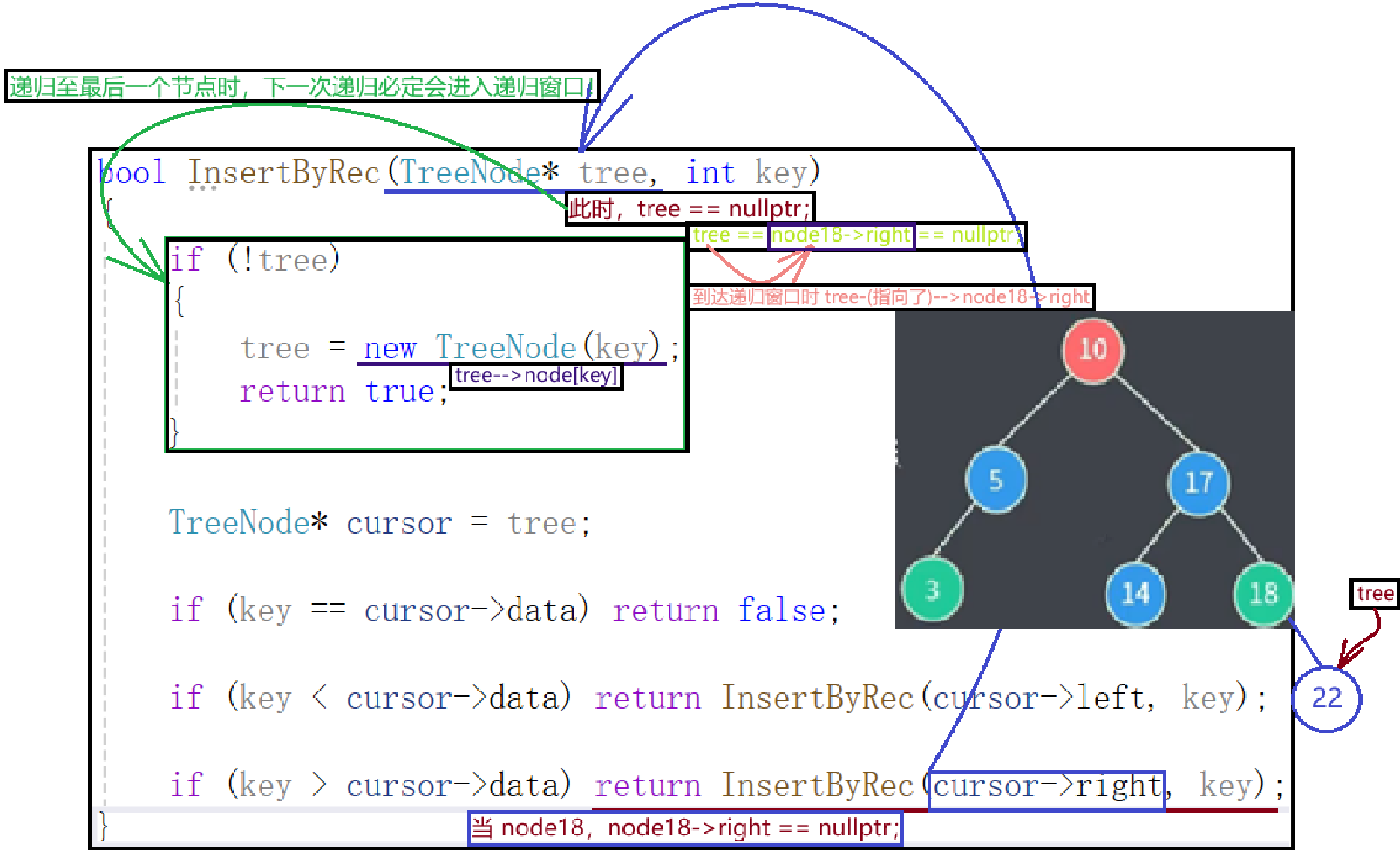
🚫🚫🚫严重错误递归代码:

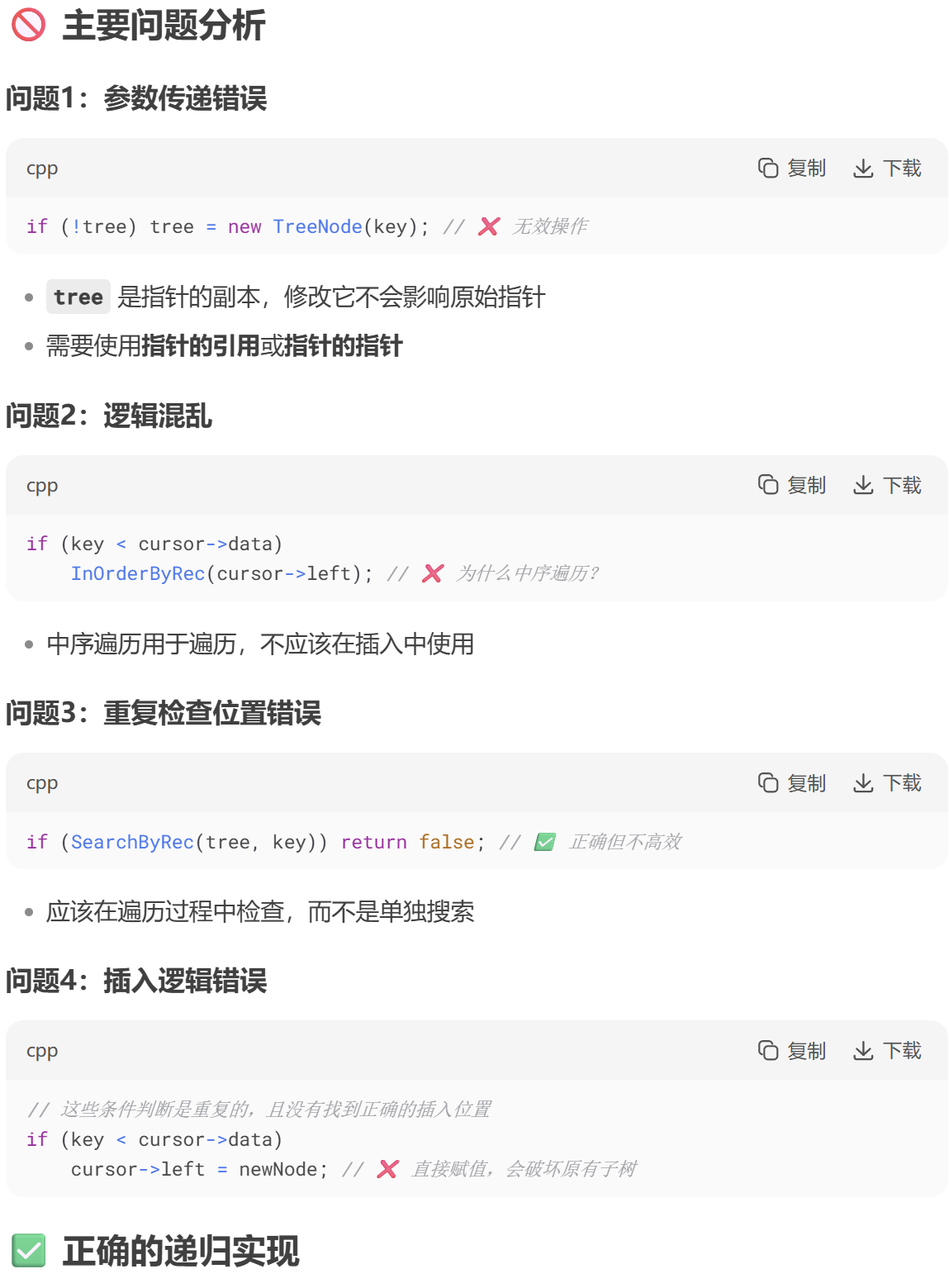
现在的疑问希望未来可以解答:
为什么需要返回递归结果?并且 A如何使最后那一节点指向 TreeNode(key)?

🚫🚫🚫我懂了!!!!为什么我的代码出现了巨大错误!!
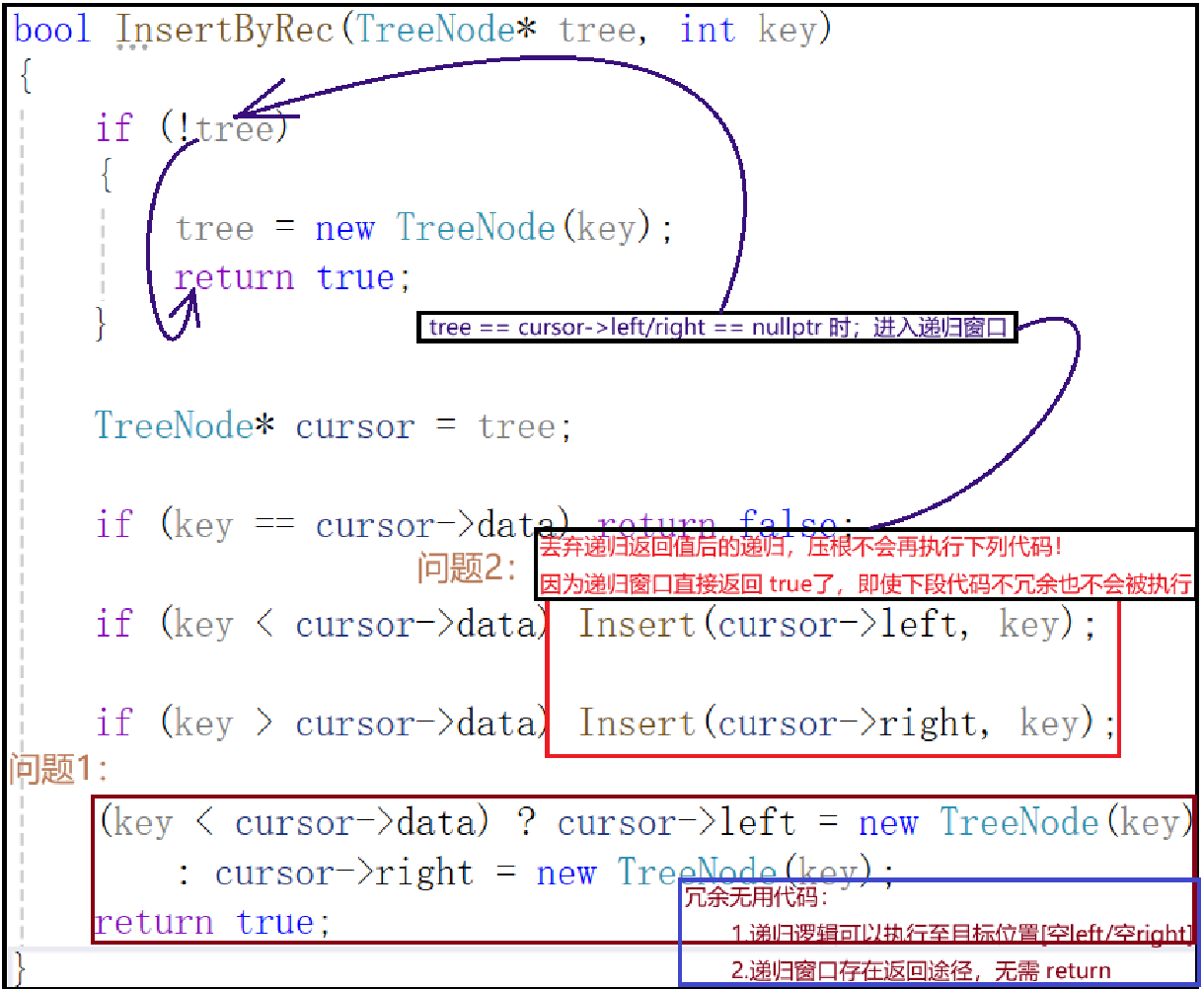
3.3二叉搜索树删除逻辑
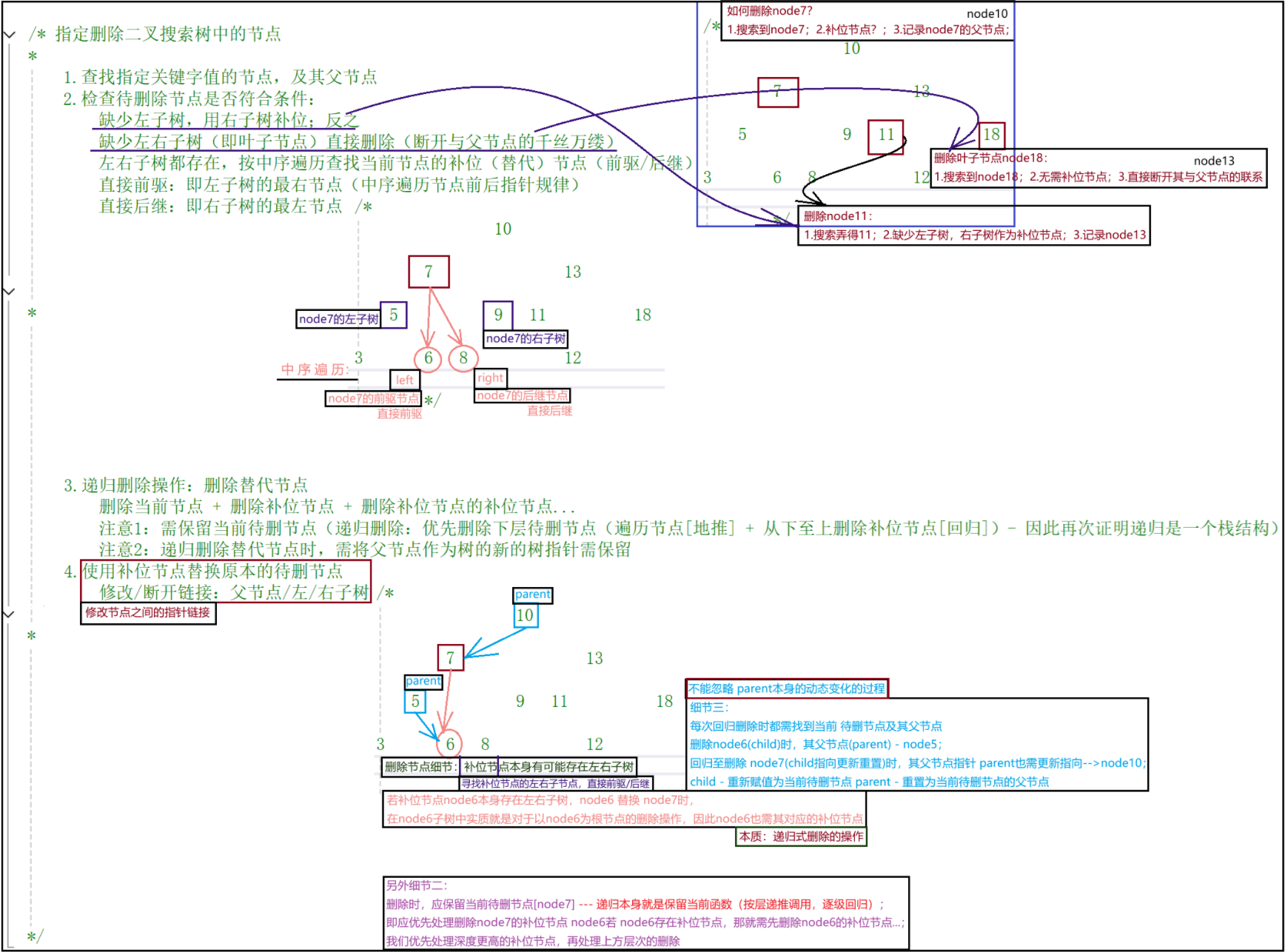
指定删除二叉搜索树中的节点:
-
1.查找指定关键字值的节点,及其父节点
-
2.检查待删除节点是否符合条件:
-
缺少左子树,用右子树补位;反之;(左右子树不共存)
-
缺少左右子树(即叶子节点)直接删除(断开与父节点的千丝万缕)
-
左右子树都存在,按中序遍历查找当前节点的补位(替代)节点(前驱/后继)
直接前驱:即左子树的最右节点(中序遍历节点前后指针规律)
直接后继:即右子树的最左节点
-
-
3.递归删除操作:删除替代节点
- 删除当前节点 + 删除补位节点 + 删除补位节点的补位节点…
- 注意1:需保留当前待删节点(递归删除:优先删除下层待删节点(遍历节点[地推] + 从下至上删除补位节点[回归])- 因此再次证明递归是一个栈结构)
- 注意2:递归删除替代节点时,需将父节点作为树的新的树指针需保留
-
4.使用补位节点替换原本的待删节点
- 修改/断开链接:父节点/左/右子树

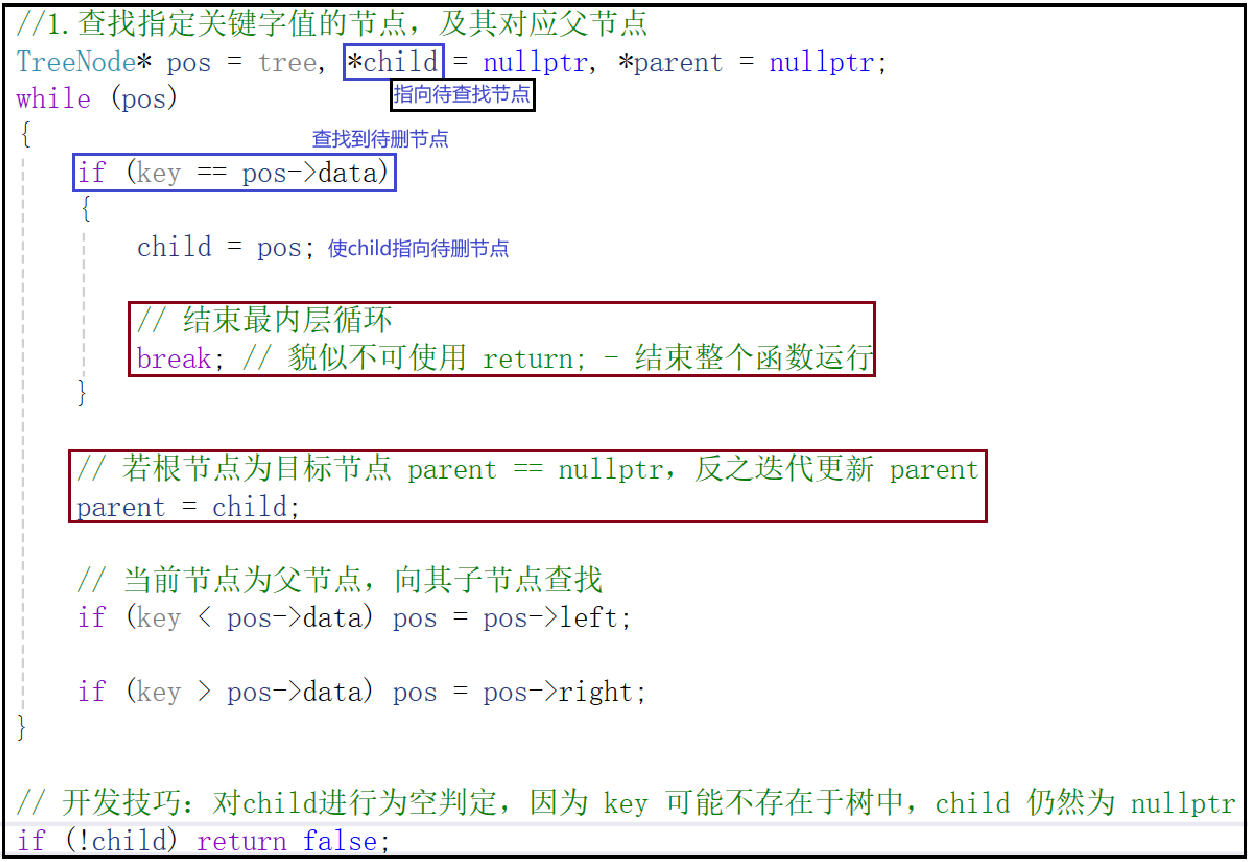
bool Delete(TreeNode* tree, int key)
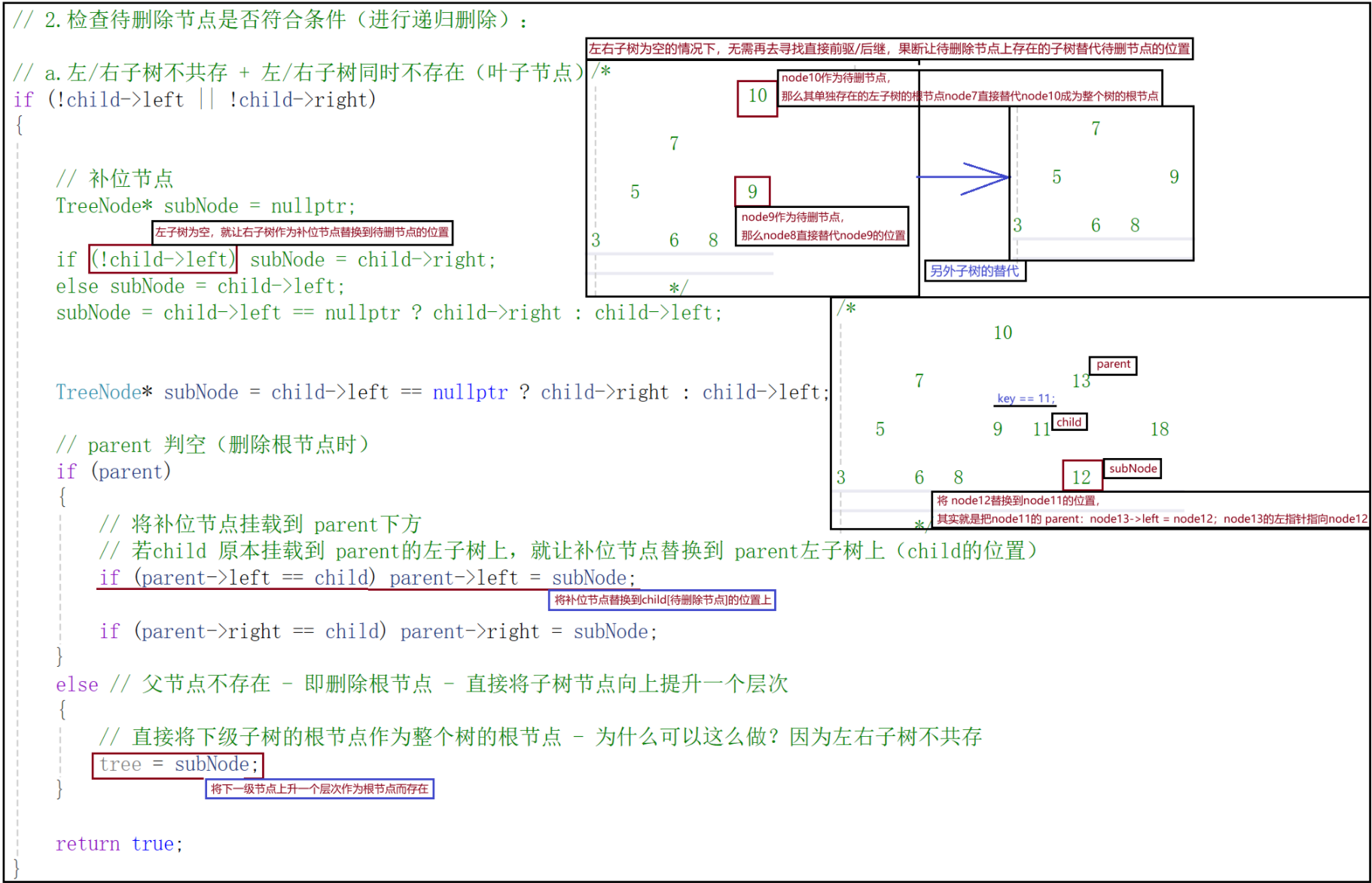
{if (!tree) return false;//1.查找指定关键字值的节点,及其对应父节点TreeNode* pos = tree, *child = nullptr, *parent = nullptr;while (pos){if (key == pos->data){child = pos;// 结束最内层循环break; // 貌似不可使用 return; - 结束整个函数运行}// 若根节点为目标节点 parent == nullptr,反之迭代更新 parentparent = child; // 当前节点为父节点,向其子节点查找if (key < pos->data) pos = pos->left;if (key > pos->data) pos = pos->right;}// 开发技巧:对child进行为空判定,因为 key 可能不存在于树中,child 仍然为 nullptrif (!child) return false;// 2.检查待删除节点是否符合条件(进行递归删除):// a.左/右子树不共存 + 左/右子树同时不存在(叶子节点)if (!child->left || !child->right){
/*// 补位节点TreeNode* subNode = nullptr;if (!child->left) subNode = child->right;else subNode = child->left;subNode = child->left == nullptr ? child->right : child->left;
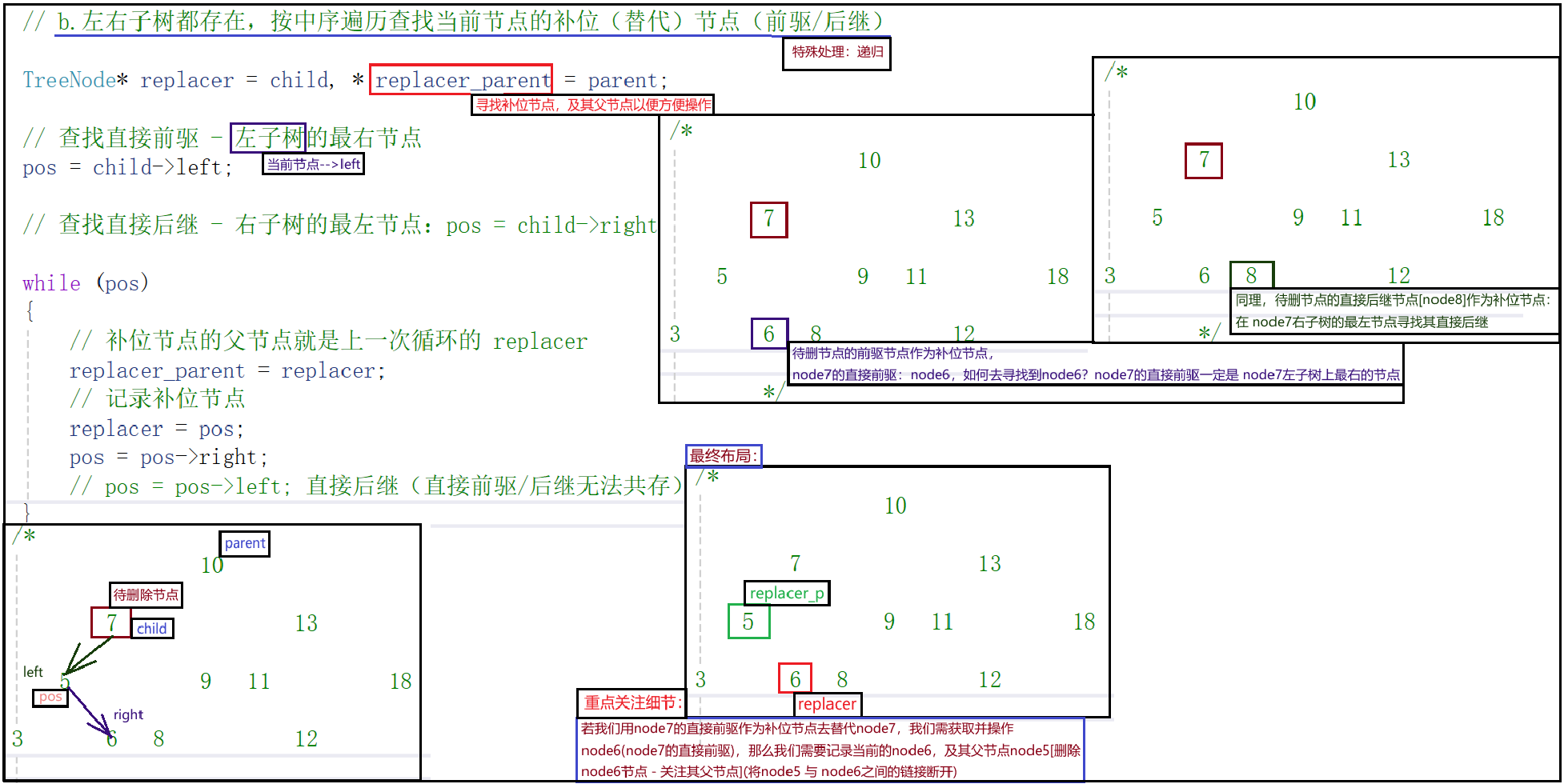
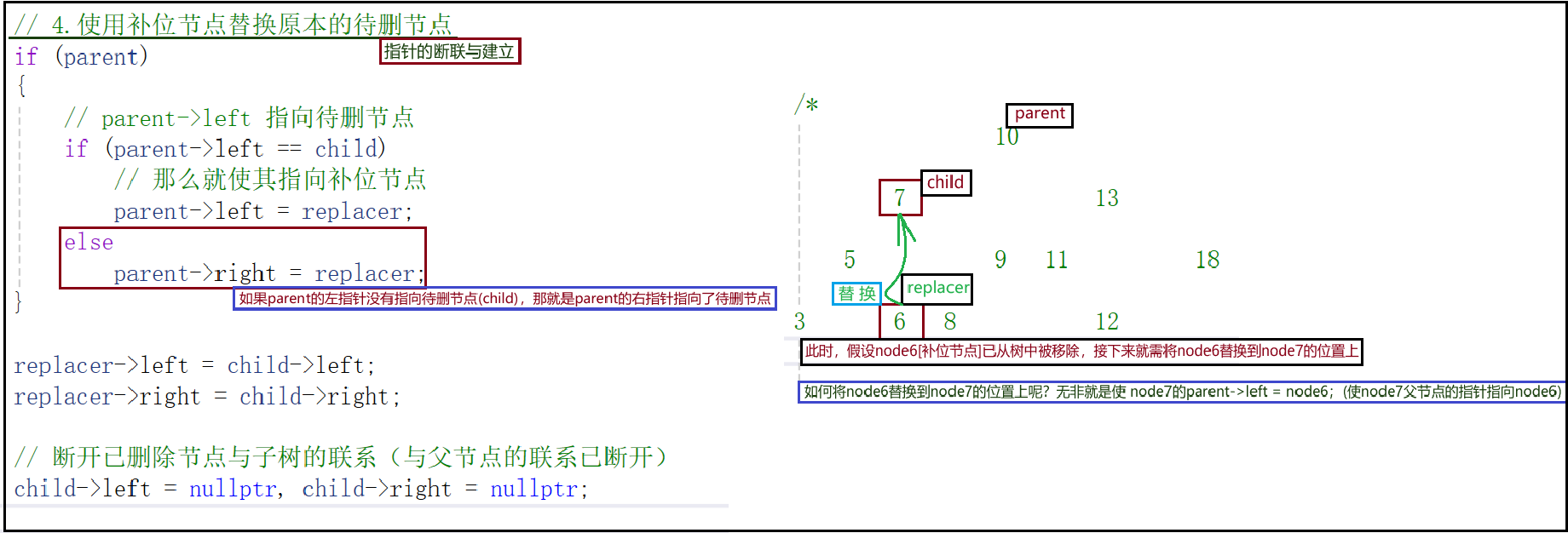
*/TreeNode* subNode = child->left == nullptr ? child->right : child->left;// parent 判空(删除根节点时)if (parent){// 将补位节点挂载到 parent下方// 若child 原本挂载到 parent的左子树上,就让补位节点替换到 parent左子树上(child的位置)if (parent->left == child) parent->left = subNode;if (parent->right == child) parent->right = subNode;}else // 父节点不存在 - 即删除根节点 - 直接将子树节点向上提升一个层次{// 直接将下级子树的根节点作为整个树的根节点 - 为什么可以这么做?因为左右子树不共存tree = subNode;}return true;}// b.左右子树都存在,按中序遍历查找当前节点的补位(替代)节点(前驱/后继)TreeNode* replacer = child, * replacer_parent = parent;// 查找直接前驱 - 左子树的最右节点pos = child->left;// 查找直接后继 - 右子树的最左节点:pos = child->right;while (pos){// 补位节点的父节点就是上一次循环的 replacerreplacer_parent = replacer;// 记录补位节点replacer = pos;pos = pos->right;// pos = pos->left; 直接后继(直接前驱/后继无法共存)}// 3.递归删除操作:删除替代节点// 树根 - replacer_parent; 待删除内容 - replacer->dataDelete(replacer_parent, replacer->data);// 4.使用补位节点替换原本的待删节点if (parent){// parent->left 指向待删节点if (parent->left == child)// 那么就使其指向补位节点parent->left = replacer;elseparent->right = replacer;}replacer->left = child->left;replacer->right = child->right;// 断开已删除节点与子树的联系(与父节点的联系已断开)child->left = nullptr, child->right = nullptr;
}
分段逻辑剖析:

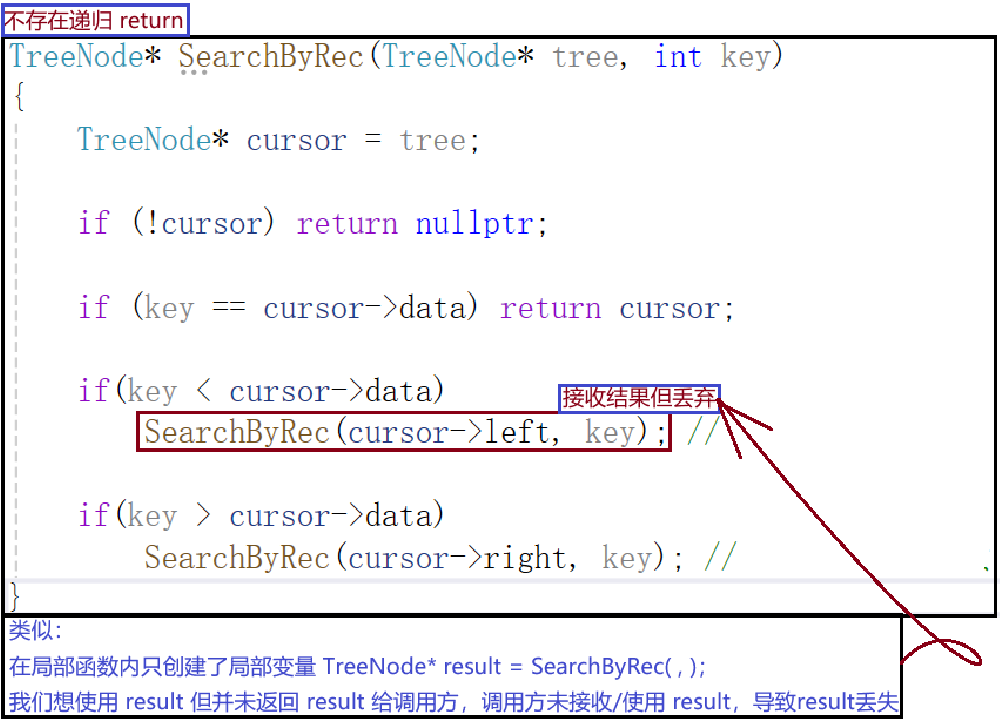
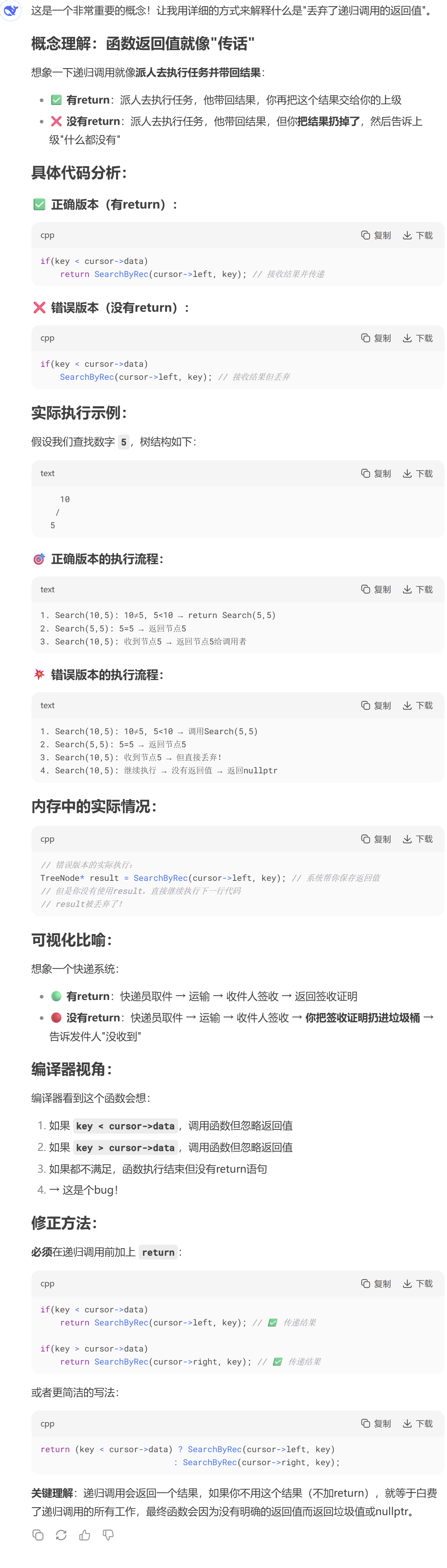
3.4丢弃递归返回值问题
黄金法则:每个递归调用都应有对应的return语句来传递结果,确保返回值沿着调用链正确传递



🌟 各位看官好,我是工藤新一¹呀~
🌈 愿各位心中所想,终有所致!
