一元函数的情况
设x*为准确值,y* =f(x*), x 为对应的近似值,y = f(x). 由函数泰勒展开式可得
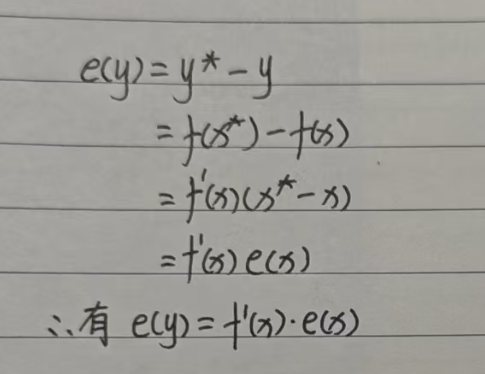
以防有小伙伴忘记泰勒,先回顾一下泰勒展开式吧
泰勒展开式:

因此,相对误差就是:
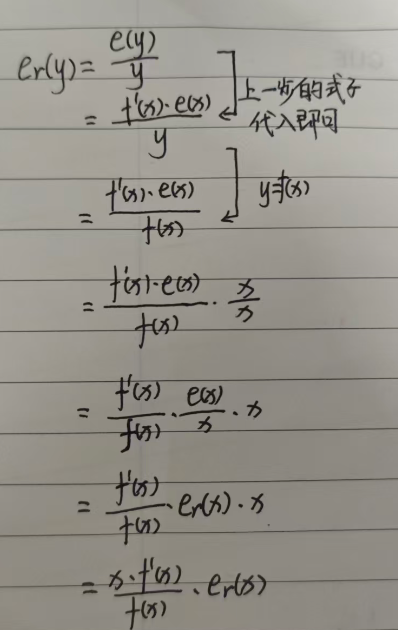
二元函数的情况
设x1*, x2* 为准确值,y* =f(x1*, x2* ), x 1,x2 为对应的近似值,y = f( x1,x2). 由二元函数泰勒展开式可得:
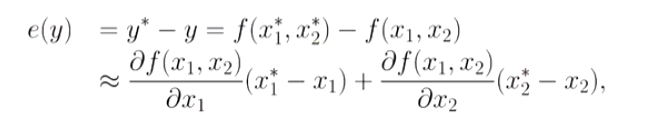
化简后可得绝对误差为:
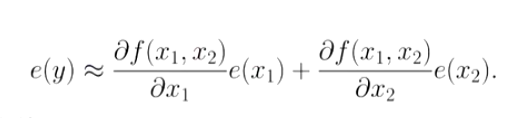
因此,相对误差就是:
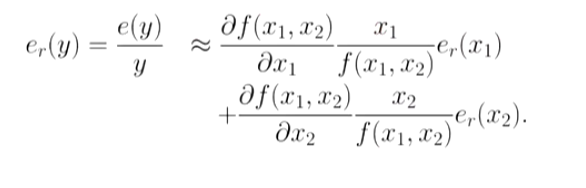
n元函数
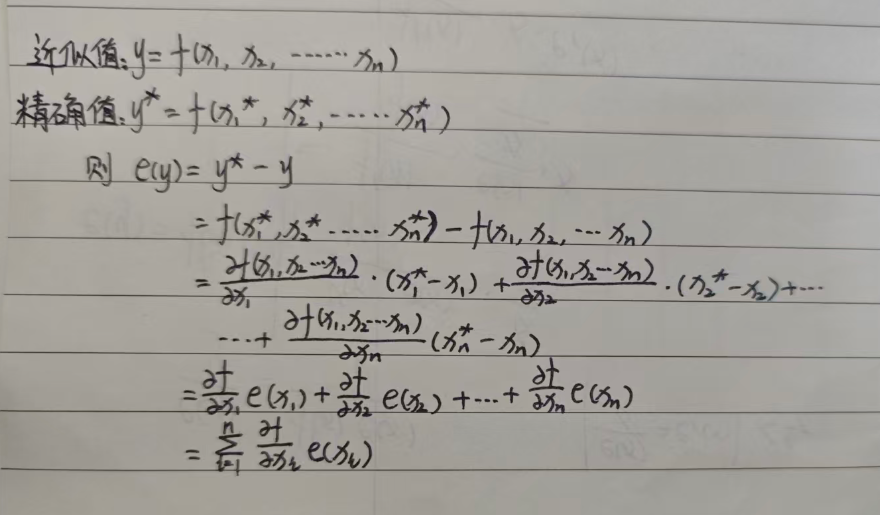
结论
绝对误差:
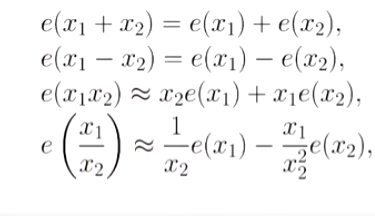
相对误差:
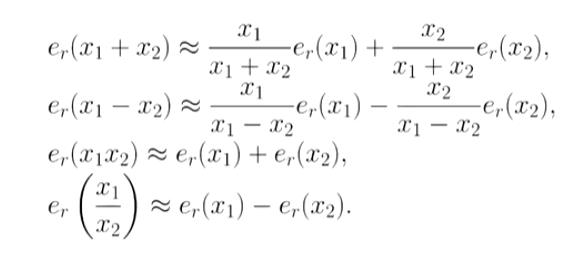
未完待更,正在努力更新中ing·····
:)